高中数学人教新课标B版必修3--《2.2.2 用样本的数字特征估计总体的数字特征》课件4(共15张PPT)
文档属性
| 名称 | 高中数学人教新课标B版必修3--《2.2.2 用样本的数字特征估计总体的数字特征》课件4(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 547.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-26 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
人民教育出版社B版
必修三
第二章 统计
2.2.2 用样本的数字特征
估计总体的数字特征
【学习目标】
1.学会计算数据的方差、标准差,理解样本数据的方差,
标准差的意义和作用,领会通过样本对总体的稳定性
水平作出科学的估计的思想。
2.如何由直方图来估算中位数、平均值
①.方差和标准差计算公式:
设一组样本数据
其平均数为
样本方差为 :
样本标准差 :
②.方差和标准差的意义:
描述的是一组数据围绕平均数波动的大小。
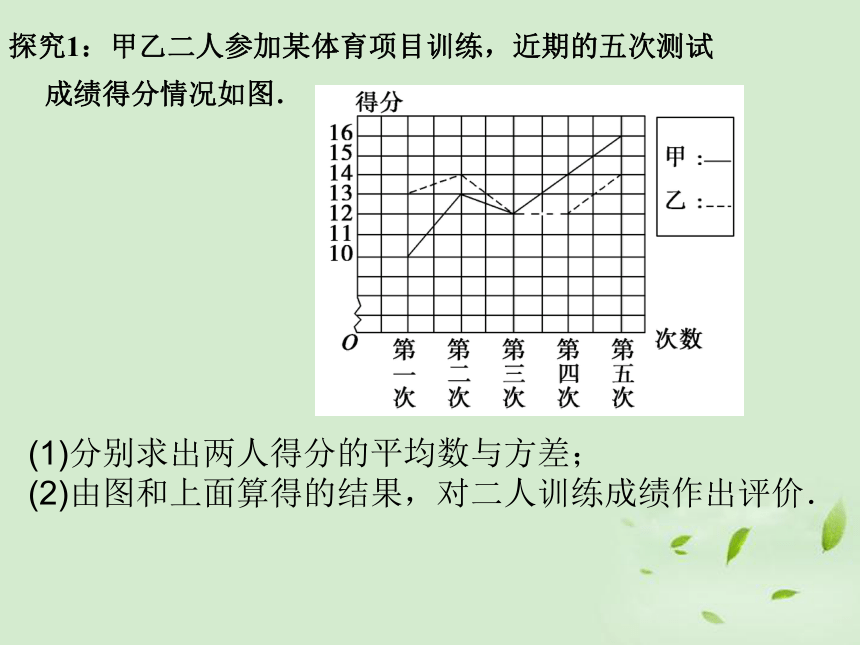
探究1:甲乙二人参加某体育项目训练,近期的五次测试
成绩得分情况如图.
(1)分别求出两人得分的平均数与方差;
(2)由图和上面算得的结果,对二人训练成绩作出评价.
解:(1)由图像可得甲、乙两人五次测试的成绩分别为
甲:10、13、12、14、16 乙:13、14、12、12、14
从折线图看,甲的成绩基本呈上升状态,而乙的成绩上下波动,
可知甲的成绩在不断提高,而乙的成绩则无明显提高.
规律技巧
1.平均数是反映一组数据的平均水平,而方差是反映一组数据稳定与波动、集中与分散的程度,当平均数相同时,方差越小越稳定.
2.在实际决策中,是否一定采用方差小的一种方案?
提示 当平均数差异较大时,不必考虑方差;
在体育比赛中,若两人平均水平都比对手稍差,
则应选派方差大的,以期超水平发挥.
探究2: 据悉2017年某省高考要将体育成绩作为参考,为此,A市为了了解今年高中毕业生的体能状况,从某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0 m(精确到0.1 m)以上的为合格.把所得数据进行整理后,分成6组,并画出频率分布直方图的一部分如图所示.已知从左到右前5个小组对应矩形的高分别为0.04,0.10, 0.14, 0.28, 0.30,且第6小组的频数是7.
1)求这次铅球测试成绩合格人数;
2)若由直方图来估计这组数据的
中位数,指出该中位数在第几组内,并说明理由.
3)估算这组数据的平均值
4)若标准差为1.3,则有多少人
在区间
规律技巧
1.根据频率分布直方图求中位数:
中位数把矩形面积一分为二的数,频率之和为0.5的数.
2.根据频率分布直方图求平均数:
平均数为各组的中间值与相应频率的积.
2.若
的方差为
,则
的方差为 .
1.判断:样本的平均数就是总体的平均数 ( )
方差的两个性质
数据 平均数 方差
3.在一次歌手大奖赛上,七位评委为歌手打出的分数如下:
去掉一个最高分和一个最低分后,
所剩数据的平均值和方差分别为 ( )
B.
C.
D.
A.
D
4.如图是某学校一名篮球运动员在五场比赛中所得分数的茎叶图,则
该运动员在这五场比赛中得分的方差________.
5.为了考察甲,乙两种小麦的长势,分别从中抽取
10株苗,测得苗高如下:
甲 12 13 14 15 10 16 13 11 15 11
乙 11 16 17 14 13 19 6 8 10 16
哪种小麦长得比较整齐?为什么
6.已知下列结论:
①一组数据
的平均数是
,则
②众数是一组数据中相同数据出现最多的次数;
③给定的一组数据的平均数一定只有一个;
④给定的一组数据的众数一定只有一个.
其中正确的结论是( )
A.①②③ B.①④ C.①③ D.③④
7. 从高三抽出50名学生参加数学竞赛,由成绩得到如下
的频率分布直方图.
由于一些数据丢失,试利用频率分布直方图求:
(1)这50名学生成绩的众数与中位数;
(2)这50名学生的平均成绩.
8.小试高考某城市100户居民的月平均用电量(单位:度),
以
分组的频率分布直方图如图.
(1)求直方图中 的值; 2)求月平均用电量的众数和中位数;
(3) 在月平均用电量为
的四组用户中,用分层抽样
的方法抽取11户居民,
则月平均用电量在
的用户中应抽取多少户
用样本的数据特征估计总体的数据特征
(1)用样本的平均数估计总体的平均数;
(2)用样本的方差估计总体的方差;
归纳与小结
(3)样本的平均数与频率分布直方图的关系;
(4)样本标准差与频率分布直方图的关系;
人民教育出版社B版
必修三
第二章 统计
2.2.2 用样本的数字特征
估计总体的数字特征
【学习目标】
1.学会计算数据的方差、标准差,理解样本数据的方差,
标准差的意义和作用,领会通过样本对总体的稳定性
水平作出科学的估计的思想。
2.如何由直方图来估算中位数、平均值
①.方差和标准差计算公式:
设一组样本数据
其平均数为
样本方差为 :
样本标准差 :
②.方差和标准差的意义:
描述的是一组数据围绕平均数波动的大小。
探究1:甲乙二人参加某体育项目训练,近期的五次测试
成绩得分情况如图.
(1)分别求出两人得分的平均数与方差;
(2)由图和上面算得的结果,对二人训练成绩作出评价.
解:(1)由图像可得甲、乙两人五次测试的成绩分别为
甲:10、13、12、14、16 乙:13、14、12、12、14
从折线图看,甲的成绩基本呈上升状态,而乙的成绩上下波动,
可知甲的成绩在不断提高,而乙的成绩则无明显提高.
规律技巧
1.平均数是反映一组数据的平均水平,而方差是反映一组数据稳定与波动、集中与分散的程度,当平均数相同时,方差越小越稳定.
2.在实际决策中,是否一定采用方差小的一种方案?
提示 当平均数差异较大时,不必考虑方差;
在体育比赛中,若两人平均水平都比对手稍差,
则应选派方差大的,以期超水平发挥.
探究2: 据悉2017年某省高考要将体育成绩作为参考,为此,A市为了了解今年高中毕业生的体能状况,从某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0 m(精确到0.1 m)以上的为合格.把所得数据进行整理后,分成6组,并画出频率分布直方图的一部分如图所示.已知从左到右前5个小组对应矩形的高分别为0.04,0.10, 0.14, 0.28, 0.30,且第6小组的频数是7.
1)求这次铅球测试成绩合格人数;
2)若由直方图来估计这组数据的
中位数,指出该中位数在第几组内,并说明理由.
3)估算这组数据的平均值
4)若标准差为1.3,则有多少人
在区间
规律技巧
1.根据频率分布直方图求中位数:
中位数把矩形面积一分为二的数,频率之和为0.5的数.
2.根据频率分布直方图求平均数:
平均数为各组的中间值与相应频率的积.
2.若
的方差为
,则
的方差为 .
1.判断:样本的平均数就是总体的平均数 ( )
方差的两个性质
数据 平均数 方差
3.在一次歌手大奖赛上,七位评委为歌手打出的分数如下:
去掉一个最高分和一个最低分后,
所剩数据的平均值和方差分别为 ( )
B.
C.
D.
A.
D
4.如图是某学校一名篮球运动员在五场比赛中所得分数的茎叶图,则
该运动员在这五场比赛中得分的方差________.
5.为了考察甲,乙两种小麦的长势,分别从中抽取
10株苗,测得苗高如下:
甲 12 13 14 15 10 16 13 11 15 11
乙 11 16 17 14 13 19 6 8 10 16
哪种小麦长得比较整齐?为什么
6.已知下列结论:
①一组数据
的平均数是
,则
②众数是一组数据中相同数据出现最多的次数;
③给定的一组数据的平均数一定只有一个;
④给定的一组数据的众数一定只有一个.
其中正确的结论是( )
A.①②③ B.①④ C.①③ D.③④
7. 从高三抽出50名学生参加数学竞赛,由成绩得到如下
的频率分布直方图.
由于一些数据丢失,试利用频率分布直方图求:
(1)这50名学生成绩的众数与中位数;
(2)这50名学生的平均成绩.
8.小试高考某城市100户居民的月平均用电量(单位:度),
以
分组的频率分布直方图如图.
(1)求直方图中 的值; 2)求月平均用电量的众数和中位数;
(3) 在月平均用电量为
的四组用户中,用分层抽样
的方法抽取11户居民,
则月平均用电量在
的用户中应抽取多少户
用样本的数据特征估计总体的数据特征
(1)用样本的平均数估计总体的平均数;
(2)用样本的方差估计总体的方差;
归纳与小结
(3)样本的平均数与频率分布直方图的关系;
(4)样本标准差与频率分布直方图的关系;
