高中数学人教新课标B版必修3--《3.4 概率的应用》课件4(共24张PPT)
文档属性
| 名称 | 高中数学人教新课标B版必修3--《3.4 概率的应用》课件4(共24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-26 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
3.4 概率的应用
人教B版高中数学必修3
复习回顾:
1、概率是描述随机事件发生可能性大小的度量,它已经渗透到人们的日常生活中,概率的取值范围是 之间的一个数,它度量事件发生的可能性.小概率事件概率接近 很少发生,而大概率事件概率接近 则经常发生.
0~1
0
1
2、概率是可以通过频率来“测量”的,所以说 是概率的一个近似。
频率
你知道概率在生活中有哪些应用么?
应用一:程序设计
为什么键盘上的按键不是按照英文字母表A,B,C,D,E……的顺序排列呢?你知道为什么吗?
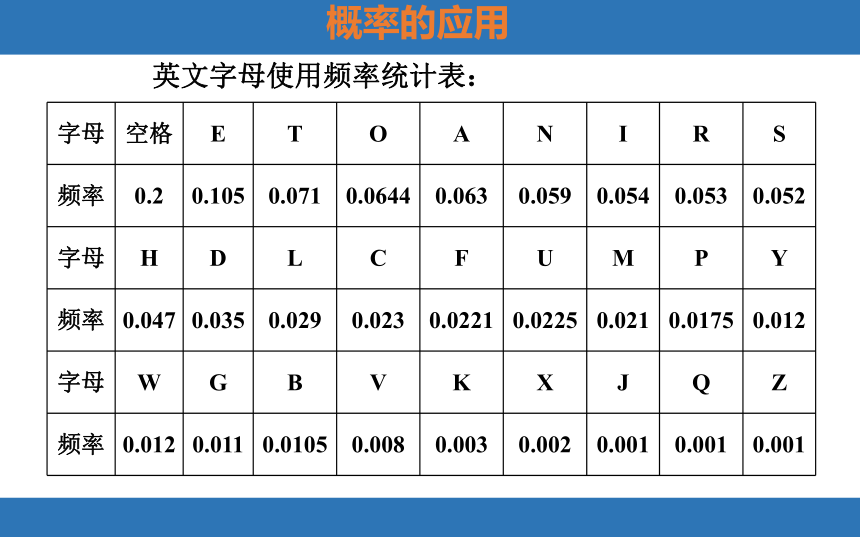
英文字母使用频率统计表:
字母 空格 E T O A N I R S
频率 0.2 0.105 0.071 0.0644 0.063 0.059 0.054 0.053 0.052
字母 H D L C F U M P Y
频率 0.047 0.035 0.029 0.023 0.0221 0.0225 0.021 0.0175 0.012
字母 W G B V K X J Q Z
频率 0.012 0.011 0.0105 0.008 0.003 0.002 0.001 0.001 0.001
shu
▼ 1 数 2 书 3 树 4 属 5 署 6 输 7 淑 8 术 9 舒
应用二:密码技术
应用二:密码技术
明文
密钥
密文
密钥
明文
密码战,向来是人类智力最残酷、最高级的较量。古罗马伟大的军事和政治家凯撒大帝把明文中的每个字母按拉丁字母次序后移三位之后的字母来代替,形成密文。接收方收到密文后,将每个字母前移三位后便得到明文。这是一种原始的编制密码方法。聪明人制造了密码,等待更聪明的人去毁灭它……
数学故事:
明文
密钥:后移三位
密文
a
d
b
e
c
f
x
a
y
b
z
c
……
你知道是如何破译的吗?
明文:“We will start the fight at eleven O’ clock on Wednesday . ”
密文:“Zh zloo vwduw wkh iljkw dw hohyhq r’ forfn rq hgqhvgdb . ”
密钥:后移三位
英文字母使用频率统计表:
字母 空格 E T O A N I R S
频率 0.2 0.105 0.071 0.0644 0.063 0.059 0.054 0.053 0.052
字母 H D L C F U M P Y
频率 0.047 0.035 0.029 0.023 0.0221 0.0225 0.021 0.0175 0.012
字母 W G B V K X J Q Z
频率 0.012 0.011 0.0105 0.008 0.003 0.002 0.001 0.001 0.001
明文:“We will start the fight at eleven O’ clock on Wednesday”
密文:“Zh zloo vwduw wkh iljkw dw hohyhq r’ forfn rq Zhgqhvgdb”。
仔细观察密文,请问密文中那个字母出现的频率最高?出现了多少次?
7个h……
提问:密文中出现次数最多的“h”一定是“e”?如果不是,怎么办?
现代保密系统为了确保每个字母出现在密文中的概率都相等,它在1到26之间随机取值,
注意,尽管在明文中“E”出现3次,但是在密文XSQWHV中却是用三个不同的字母来替换的.
例如:19,7,12,1,3,8,……
这时“ELEVEN”这个词,用E后面第19个字母X表示E,
用L后面第7个字母S表示L……
因此,ELEVEN变成了XSQWHV.
这就是一种理论上不可破译的密码,即“一次性密码本”(用后立即销毁).
应用三:社会调查
人们希望在调查中得到诚实的回答,但是有些敏感问题参与调查者常常不愿意如实回答。
你服用过兴奋剂吗?”
1965年Stanley L. Warner(沃纳)发明了一种应用概率知识来消除这种不愿意情绪的方法. Warner(沃纳)要求人们随机地回答所提两个问题中的一个,而不必告诉采访者回答的是哪个问题。两个问题中有一个是敏感的或者是令人为难的;另一个问题是无关紧要的。这样应答者将乐意如实地回答问题,因为只有他知道自己回答的是哪个问题。
例如在调查运动员服用兴奋剂的时候,无关紧要的问题是“你的身份证号码的尾数是奇数吗”,敏感的问题是“你服用过兴奋剂吗”,然后要求被调查的运动员掷一枚硬币,如果出现正面,就回答第一个问题,否则回答第二个问题。
数学趣闻:
掷硬币,如果出现正面,就回答第一个问题“你的身份证号码的尾数是奇数吗”,否则回答第二个问题“你服用过兴奋剂吗”
假如我们把这种方法用于200个被调查的运动员,得到54个“是”的回答,如何估算服用兴奋剂的概率?
小组讨论:
应用四:估计整体
可以使用以下的方法:
先从水库中捕出一定数量的鱼,例如2000尾,给每尾鱼作上记号,不影响其存活,然后放回水库.
经过适当的时间,让其和水库中其余的鱼充分混合,再从水库中捕出一定数量的鱼,例如500尾,查看其中有记号的鱼,设有40尾.
根据上述数据,你能估计出水库内鱼的尾数么?
问题:如何估计水库中的鱼的尾数?
课堂小结:
一、程序设计;
二、密码技术;
三、社会调查;
四、估计整体。
作业:
学案(概率的应用)应用举例1、2.
a b c d E F G H i j k l m
1 2 3 4 5 6 7 8 9 10 11 12 13
n o p q R S T U v w x y z
14 15 16 17 18 19 20 21 22 23 24 25 26
[课后作业]
1.现代社会对破译密码的要求越来越高,有一种密码把英文的明文(真实文)按字母分解,其中英文的a,b,c,…,z的26个字母(不论大小写)依次对应1,2,3,…,26,这26个自然数,见表格:
a b c d e f g h i j k l m
1 2 3 4 5 6 7 8 9 10 11 12 13
n o p q r s t u v w x y z
14 15 16 17 18 19 20 21 22 23 24 25 26
a b c d e f g h i j k l m
1 2 3 4 5 6 7 8 9 10 11 12 13
n o p q r s t u v w x y z
14 15 16 17 18 19 20 21 22 23 24 25 26
C
C
[课后作业]
2.某水产试验场实行某种鱼的人工孵化,10000个鱼卵能孵出8513尾鱼苗,根据概率的统计定义解答下列问题:
(1)求这种鱼卵的孵化概率(孵化率);
(2) 30000个鱼卵大约能孵化多少尾鱼苗?
(3)要孵化50000尾鱼苗,大概得备多少鱼卵?(列式即可)
0.8513
25539
3.4 概率的应用
人教B版高中数学必修3
复习回顾:
1、概率是描述随机事件发生可能性大小的度量,它已经渗透到人们的日常生活中,概率的取值范围是 之间的一个数,它度量事件发生的可能性.小概率事件概率接近 很少发生,而大概率事件概率接近 则经常发生.
0~1
0
1
2、概率是可以通过频率来“测量”的,所以说 是概率的一个近似。
频率
你知道概率在生活中有哪些应用么?
应用一:程序设计
为什么键盘上的按键不是按照英文字母表A,B,C,D,E……的顺序排列呢?你知道为什么吗?
英文字母使用频率统计表:
字母 空格 E T O A N I R S
频率 0.2 0.105 0.071 0.0644 0.063 0.059 0.054 0.053 0.052
字母 H D L C F U M P Y
频率 0.047 0.035 0.029 0.023 0.0221 0.0225 0.021 0.0175 0.012
字母 W G B V K X J Q Z
频率 0.012 0.011 0.0105 0.008 0.003 0.002 0.001 0.001 0.001
shu
▼ 1 数 2 书 3 树 4 属 5 署 6 输 7 淑 8 术 9 舒
应用二:密码技术
应用二:密码技术
明文
密钥
密文
密钥
明文
密码战,向来是人类智力最残酷、最高级的较量。古罗马伟大的军事和政治家凯撒大帝把明文中的每个字母按拉丁字母次序后移三位之后的字母来代替,形成密文。接收方收到密文后,将每个字母前移三位后便得到明文。这是一种原始的编制密码方法。聪明人制造了密码,等待更聪明的人去毁灭它……
数学故事:
明文
密钥:后移三位
密文
a
d
b
e
c
f
x
a
y
b
z
c
……
你知道是如何破译的吗?
明文:“We will start the fight at eleven O’ clock on Wednesday . ”
密文:“Zh zloo vwduw wkh iljkw dw hohyhq r’ forfn rq hgqhvgdb . ”
密钥:后移三位
英文字母使用频率统计表:
字母 空格 E T O A N I R S
频率 0.2 0.105 0.071 0.0644 0.063 0.059 0.054 0.053 0.052
字母 H D L C F U M P Y
频率 0.047 0.035 0.029 0.023 0.0221 0.0225 0.021 0.0175 0.012
字母 W G B V K X J Q Z
频率 0.012 0.011 0.0105 0.008 0.003 0.002 0.001 0.001 0.001
明文:“We will start the fight at eleven O’ clock on Wednesday”
密文:“Zh zloo vwduw wkh iljkw dw hohyhq r’ forfn rq Zhgqhvgdb”。
仔细观察密文,请问密文中那个字母出现的频率最高?出现了多少次?
7个h……
提问:密文中出现次数最多的“h”一定是“e”?如果不是,怎么办?
现代保密系统为了确保每个字母出现在密文中的概率都相等,它在1到26之间随机取值,
注意,尽管在明文中“E”出现3次,但是在密文XSQWHV中却是用三个不同的字母来替换的.
例如:19,7,12,1,3,8,……
这时“ELEVEN”这个词,用E后面第19个字母X表示E,
用L后面第7个字母S表示L……
因此,ELEVEN变成了XSQWHV.
这就是一种理论上不可破译的密码,即“一次性密码本”(用后立即销毁).
应用三:社会调查
人们希望在调查中得到诚实的回答,但是有些敏感问题参与调查者常常不愿意如实回答。
你服用过兴奋剂吗?”
1965年Stanley L. Warner(沃纳)发明了一种应用概率知识来消除这种不愿意情绪的方法. Warner(沃纳)要求人们随机地回答所提两个问题中的一个,而不必告诉采访者回答的是哪个问题。两个问题中有一个是敏感的或者是令人为难的;另一个问题是无关紧要的。这样应答者将乐意如实地回答问题,因为只有他知道自己回答的是哪个问题。
例如在调查运动员服用兴奋剂的时候,无关紧要的问题是“你的身份证号码的尾数是奇数吗”,敏感的问题是“你服用过兴奋剂吗”,然后要求被调查的运动员掷一枚硬币,如果出现正面,就回答第一个问题,否则回答第二个问题。
数学趣闻:
掷硬币,如果出现正面,就回答第一个问题“你的身份证号码的尾数是奇数吗”,否则回答第二个问题“你服用过兴奋剂吗”
假如我们把这种方法用于200个被调查的运动员,得到54个“是”的回答,如何估算服用兴奋剂的概率?
小组讨论:
应用四:估计整体
可以使用以下的方法:
先从水库中捕出一定数量的鱼,例如2000尾,给每尾鱼作上记号,不影响其存活,然后放回水库.
经过适当的时间,让其和水库中其余的鱼充分混合,再从水库中捕出一定数量的鱼,例如500尾,查看其中有记号的鱼,设有40尾.
根据上述数据,你能估计出水库内鱼的尾数么?
问题:如何估计水库中的鱼的尾数?
课堂小结:
一、程序设计;
二、密码技术;
三、社会调查;
四、估计整体。
作业:
学案(概率的应用)应用举例1、2.
a b c d E F G H i j k l m
1 2 3 4 5 6 7 8 9 10 11 12 13
n o p q R S T U v w x y z
14 15 16 17 18 19 20 21 22 23 24 25 26
[课后作业]
1.现代社会对破译密码的要求越来越高,有一种密码把英文的明文(真实文)按字母分解,其中英文的a,b,c,…,z的26个字母(不论大小写)依次对应1,2,3,…,26,这26个自然数,见表格:
a b c d e f g h i j k l m
1 2 3 4 5 6 7 8 9 10 11 12 13
n o p q r s t u v w x y z
14 15 16 17 18 19 20 21 22 23 24 25 26
a b c d e f g h i j k l m
1 2 3 4 5 6 7 8 9 10 11 12 13
n o p q r s t u v w x y z
14 15 16 17 18 19 20 21 22 23 24 25 26
C
C
[课后作业]
2.某水产试验场实行某种鱼的人工孵化,10000个鱼卵能孵出8513尾鱼苗,根据概率的统计定义解答下列问题:
(1)求这种鱼卵的孵化概率(孵化率);
(2) 30000个鱼卵大约能孵化多少尾鱼苗?
(3)要孵化50000尾鱼苗,大概得备多少鱼卵?(列式即可)
0.8513
25539
