24.2.2 直线和圆的位置关系 课件(共30张PPT)
文档属性
| 名称 | 24.2.2 直线和圆的位置关系 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 703.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-26 18:40:25 | ||
图片预览






文档简介
(共30张PPT)
第二十四章 圆
24.2.2 直线和圆的位置关系
人教版九年级数学上册
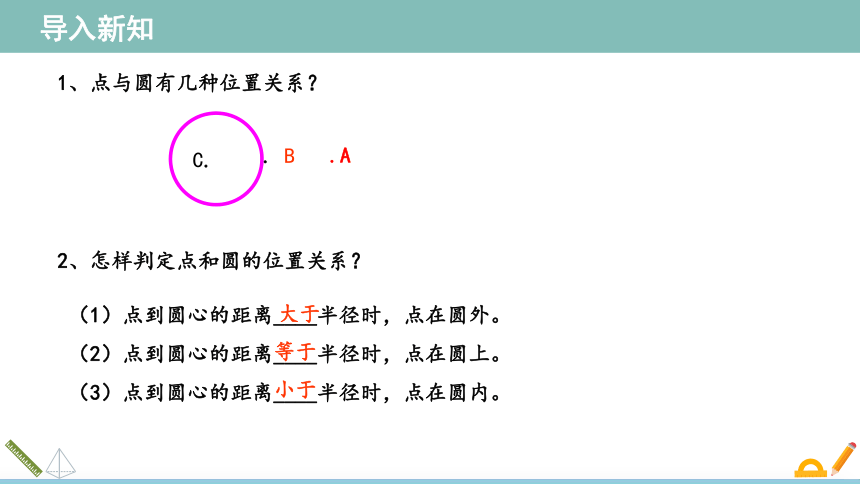
1、点与圆有几种位置关系?
2、怎样判定点和圆的位置关系?
. B
C.
(1)点到圆心的距离____半径时,点在圆外。
(2)点到圆心的距离____半径时,点在圆上。
(3)点到圆心的距离____半径时,点在圆内。
大于
等于
小于
.A
导入新知
1.知道直线和圆相交、相切、相离的概念。
2.根据具体方法判断直线和圆的位置关系。
重点难点
重点:理解直线和圆相交、相切、相离的位置关系。
难点:直线与圆三种位置关系判定的运用。
学习素养
(1)如图,在太阳升起的过程中,太阳和地平线会有几种位置关系?我们把太阳看作一个圆,地平线看作一条直线,由此你能得出直线和圆的位置关系吗?
探索新知
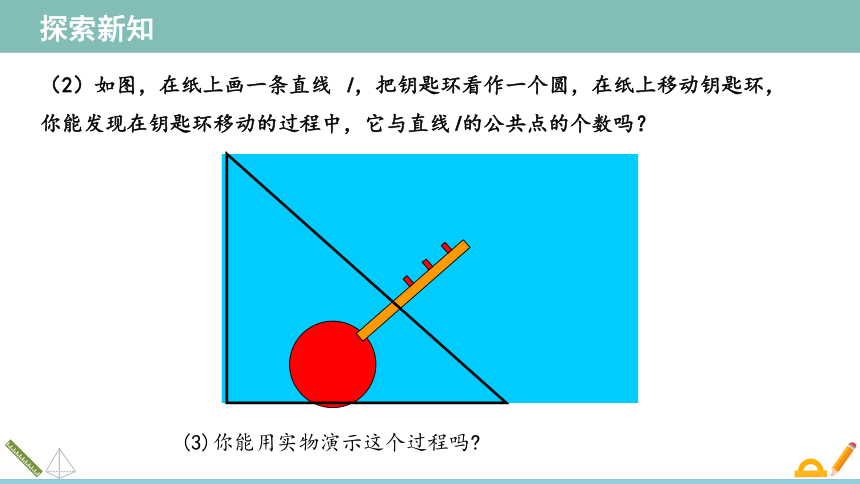
(2)如图,在纸上画一条直线 l,把钥匙环看作一个圆,在纸上移动钥匙环,你能发现在钥匙环移动的过程中,它与直线l的公共点的个数吗?
(3)你能用实物演示这个过程吗
探索新知
.O
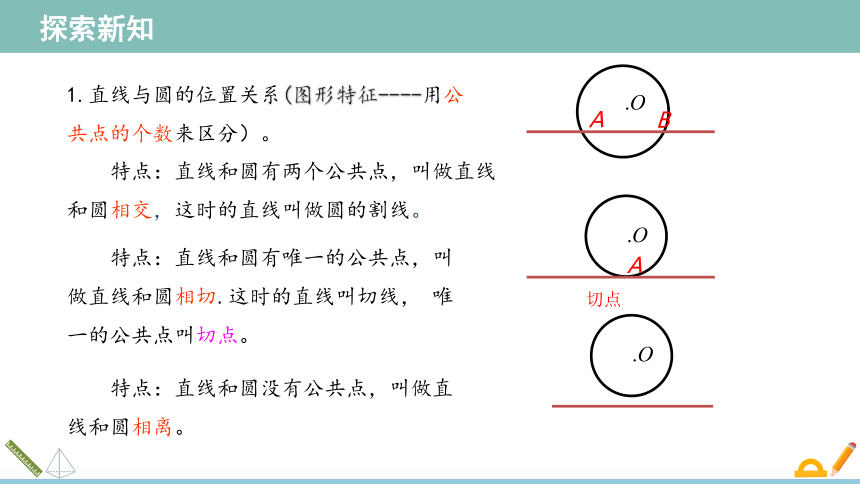
特点:直线和圆没有公共点,叫做直线和圆相离。
.O
特点:直线和圆有唯一的公共点,叫做直线和圆相切.这时的直线叫切线, 唯一的公共点叫切点。
.O
特点:直线和圆有两个公共点,叫做直线和圆相交,这时的直线叫做圆的割线。
1.直线与圆的位置关系(图形特征----用公共点的个数来区分)。
.A
.A
.B
切点
探索新知
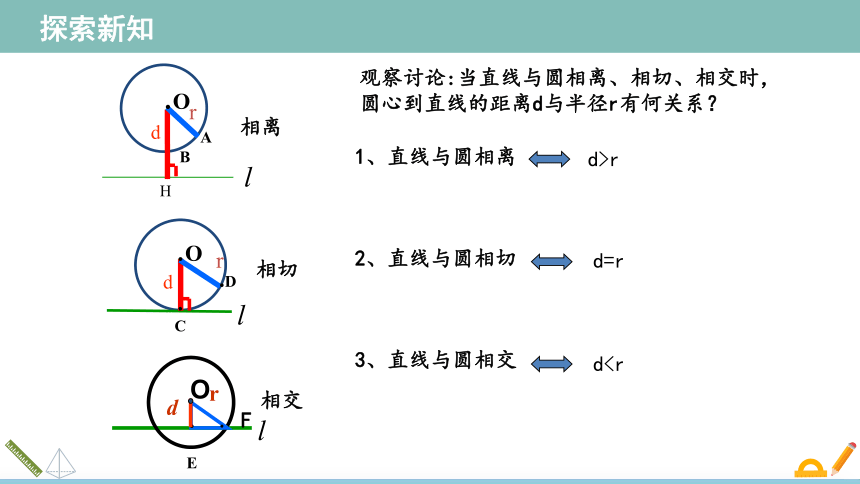
观察讨论:当直线与圆相离、相切、相交时,圆心到直线的距离d与半径r有何关系?
d
r
相离
A
d
r
相切
H
.D
.O
r
d
相交
.
C
.O
B
.
E
. F
O
1、直线与圆相离
2、直线与圆相切
3、直线与圆相交
d>r
d=r
d探索新知
判定直线 与圆的位置关系的方法有____种:
(1)根据定义,由________________的个数来判断;
(2)根据性质,由_________________的关系来判断。
在实际应用中,常采用第二种方法判定。
两
直线与圆的公共点
圆心距d与半径r
探索新知
太阳与地平线的位置关系,列车的轮子与铁轨之间的关系,都给我们直线与圆的位置关系的印象.
探索新知
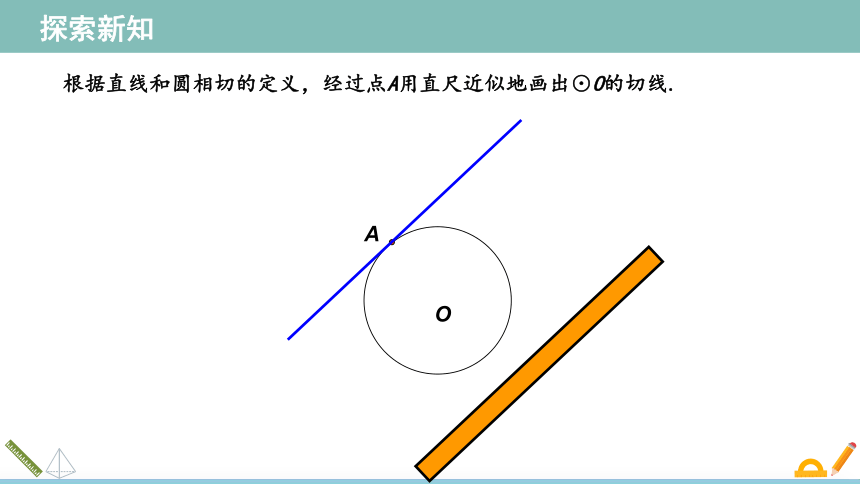
·
A
根据直线和圆相切的定义,经过点A用直尺近似地画出⊙O的切线.
O
探索新知
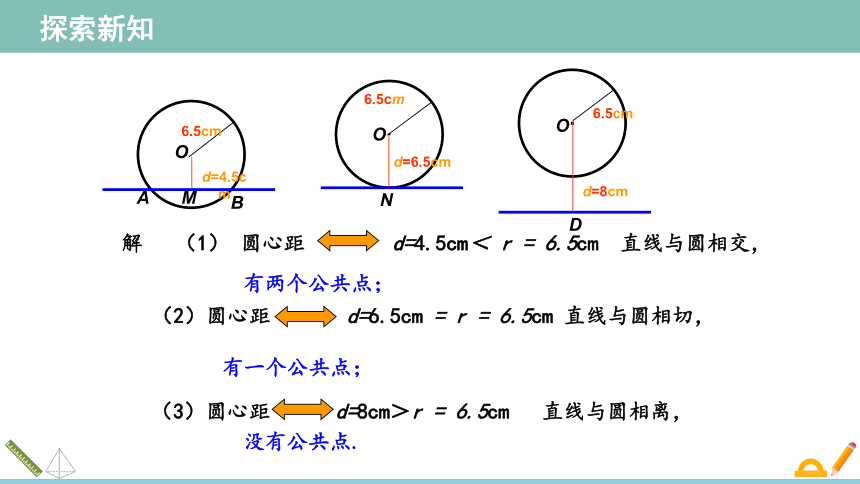
圆的直径是13cm,如果直线与圆心的距离分别是
(1)4.5cm ; (2) 6.5cm ; (3) 8cm.
那么直线与圆分别是什么位置关系? 有几个公共点?
探索新知
(3)圆心距 d=8cm>r = 6.5cm 直线与圆相离,
有两个公共点;
有一个公共点;
没有公共点.
A
B
·
6.5cm
d=4.5cm
O
M
(2)圆心距 d=6.5cm = r = 6.5cm 直线与圆相切,
·
N
O
6.5cm
d=6.5cm
解 (1) 圆心距 d=4.5cm< r = 6.5cm 直线与圆相交,
D
·
O
6.5cm
d=8cm
探索新知
直线与圆的 位置关系
图形
公共点个数
公共点名称
直线名称
2个
交点
割线
1个
切点
切线
0个
相离
相切
相交
位置关系
公共点个数
探索新知
下面我们共同完成作图后,再回答问题:
(1)任意画一个半径为r的⊙O。
(2)任意画⊙O的一条半径 OD。
(3)过D作直线l⊥OD。
l
P
D
直线l满足
第一:经过半径的外端
第二:垂直于这条半径
切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线。
探索新知
判断
1.经过半径外端的直线是圆的切线( )
2.与半径垂直的直线是圆的切线( )
l
注意:若直线满足①,
而不满足②;
若直线满足②,
而不满足①。
×
×
探索新知
直线AB经过⊙O上的点C,并且OA=OB,CA=CB,求证:直线AB是⊙O的切线.
证明: 连接OC
∵ 在△OAB中, OA=OB, CA=CB
∴OC⊥AB
∴AB是⊙O的切线
∵ OC为⊙O的半径
探索新知
如果知道直线是圆的切线,有什么性质定理呢?
圆的切线垂直于经过切点的半径。
探索新知
AB是⊙O的弦,C是⊙O外一点,BC是⊙O的切线,AB交过C点的直径于点D,OA⊥CD,试判断△BCD的形状,并
说明你的理由.
探索新知
AB是⊙O的直径,AE平分∠BAC交⊙O于点E,过点E作⊙O的切线交AC的延长线于点D,试判断△AED的形状,并说明理由.
探索新知
在△ABC中,AB=10cm,BC=6cm,AC=8cm,
(1)若以C为圆心,4 cm长为半径画⊙C,则⊙C与AB的位置关系怎样?
(2)若要使AB与⊙C 相切,则⊙C的半径应当是多少?
(3)若要以AC为直径画⊙O,则⊙O与AB、BC的位置关系分别怎样?
课堂检测
解:过C作CD⊥AB,垂足为D .
因为BC2+AC2=62+82=100,AB2=102=100,
所以BC2+AC2= AB2,故△ABC是直角三角形,根据三角形面积相等得:
(1)若以C为圆心,4cm长为半径画⊙C ,因为4cm<4.8cm,所以⊙C与AB的位置关系为相离.
(2)若要使AB与⊙C相切,则⊙C的半径应为4.8cm .
(3)若以AC为直径画⊙O,由于BC⊥AC,故⊙O与BC相切;⊙O与AB相交.
课堂检测
如图,PA、PB是⊙O的切线,切点分别是点A、B,直线EF也是⊙O的切线,切点为点Q,分别交PA、PB于点F、E.已知PA=12 cm,求△PEF的周长。
课堂检测
分析:根据切线长定理,得PA=PB,EB=EQ,FQ=FA,从而可将求△PEF的周长转化为求2PA的值.
解答:∵PA、PB是⊙O的切线,
∴PA=PB.
又∵直线EF是⊙O的切线,
∴EB=EQ,FQ=FA,
∴△PEF的周长=PE+PF+EF=PE+PF+EB+FA=PA+PB=2PA=24cm.
课堂检测
如图,在△ABC中,∠A=66°,点I是内心,则∠BIC的大小为( )
C
课堂检测
C
课堂检测
B
课堂检测
如图是油路管道的一部分,延伸外围的支路恰好构成一个直角三角形,两直角边分别为3 m和4 m.按照输油中心O到三条支路的距离相等来连接管道,则O到三条支路的管道总长(计算时视管道为线,中心O为点)是( )
B
课堂检测
.O
特点:直线和圆没有公共点,叫做直线和圆相离。
.O
特点:直线和圆有唯一的公共点,叫做直线和圆相切.这时的直线叫切线, 唯一的公共点叫切点。
.O
特点:直线和圆有两个公共点,叫做直线和圆相交,这时的直线叫做圆的割线。
1.直线与圆的位置关系(图形特征----用公共点的个数来区分)。
.A
.A
.B
切点
课堂小结
切线长和切线长定理:
经过圆外一点的圆的切线上,这点和切点之间线段的长,叫做这点到圆的切线长。
切线长定理:
从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分这两条切线的夹角。
核心提示:
(1)从圆外任意一点都可以引圆的两条切线,过圆上一点只能引圆的一条切线。
(2)切线长定理主要用于证明线段相等、角相等及垂直关系。
课堂小结
人教版九年级数学上册
谢 谢
第二十四章 圆
24.2.2 直线和圆的位置关系
人教版九年级数学上册
1、点与圆有几种位置关系?
2、怎样判定点和圆的位置关系?
. B
C.
(1)点到圆心的距离____半径时,点在圆外。
(2)点到圆心的距离____半径时,点在圆上。
(3)点到圆心的距离____半径时,点在圆内。
大于
等于
小于
.A
导入新知
1.知道直线和圆相交、相切、相离的概念。
2.根据具体方法判断直线和圆的位置关系。
重点难点
重点:理解直线和圆相交、相切、相离的位置关系。
难点:直线与圆三种位置关系判定的运用。
学习素养
(1)如图,在太阳升起的过程中,太阳和地平线会有几种位置关系?我们把太阳看作一个圆,地平线看作一条直线,由此你能得出直线和圆的位置关系吗?
探索新知
(2)如图,在纸上画一条直线 l,把钥匙环看作一个圆,在纸上移动钥匙环,你能发现在钥匙环移动的过程中,它与直线l的公共点的个数吗?
(3)你能用实物演示这个过程吗
探索新知
.O
特点:直线和圆没有公共点,叫做直线和圆相离。
.O
特点:直线和圆有唯一的公共点,叫做直线和圆相切.这时的直线叫切线, 唯一的公共点叫切点。
.O
特点:直线和圆有两个公共点,叫做直线和圆相交,这时的直线叫做圆的割线。
1.直线与圆的位置关系(图形特征----用公共点的个数来区分)。
.A
.A
.B
切点
探索新知
观察讨论:当直线与圆相离、相切、相交时,圆心到直线的距离d与半径r有何关系?
d
r
相离
A
d
r
相切
H
.D
.O
r
d
相交
.
C
.O
B
.
E
. F
O
1、直线与圆相离
2、直线与圆相切
3、直线与圆相交
d>r
d=r
d
判定直线 与圆的位置关系的方法有____种:
(1)根据定义,由________________的个数来判断;
(2)根据性质,由_________________的关系来判断。
在实际应用中,常采用第二种方法判定。
两
直线与圆的公共点
圆心距d与半径r
探索新知
太阳与地平线的位置关系,列车的轮子与铁轨之间的关系,都给我们直线与圆的位置关系的印象.
探索新知
·
A
根据直线和圆相切的定义,经过点A用直尺近似地画出⊙O的切线.
O
探索新知
圆的直径是13cm,如果直线与圆心的距离分别是
(1)4.5cm ; (2) 6.5cm ; (3) 8cm.
那么直线与圆分别是什么位置关系? 有几个公共点?
探索新知
(3)圆心距 d=8cm>r = 6.5cm 直线与圆相离,
有两个公共点;
有一个公共点;
没有公共点.
A
B
·
6.5cm
d=4.5cm
O
M
(2)圆心距 d=6.5cm = r = 6.5cm 直线与圆相切,
·
N
O
6.5cm
d=6.5cm
解 (1) 圆心距 d=4.5cm< r = 6.5cm 直线与圆相交,
D
·
O
6.5cm
d=8cm
探索新知
直线与圆的 位置关系
图形
公共点个数
公共点名称
直线名称
2个
交点
割线
1个
切点
切线
0个
相离
相切
相交
位置关系
公共点个数
探索新知
下面我们共同完成作图后,再回答问题:
(1)任意画一个半径为r的⊙O。
(2)任意画⊙O的一条半径 OD。
(3)过D作直线l⊥OD。
l
P
D
直线l满足
第一:经过半径的外端
第二:垂直于这条半径
切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线。
探索新知
判断
1.经过半径外端的直线是圆的切线( )
2.与半径垂直的直线是圆的切线( )
l
注意:若直线满足①,
而不满足②;
若直线满足②,
而不满足①。
×
×
探索新知
直线AB经过⊙O上的点C,并且OA=OB,CA=CB,求证:直线AB是⊙O的切线.
证明: 连接OC
∵ 在△OAB中, OA=OB, CA=CB
∴OC⊥AB
∴AB是⊙O的切线
∵ OC为⊙O的半径
探索新知
如果知道直线是圆的切线,有什么性质定理呢?
圆的切线垂直于经过切点的半径。
探索新知
AB是⊙O的弦,C是⊙O外一点,BC是⊙O的切线,AB交过C点的直径于点D,OA⊥CD,试判断△BCD的形状,并
说明你的理由.
探索新知
AB是⊙O的直径,AE平分∠BAC交⊙O于点E,过点E作⊙O的切线交AC的延长线于点D,试判断△AED的形状,并说明理由.
探索新知
在△ABC中,AB=10cm,BC=6cm,AC=8cm,
(1)若以C为圆心,4 cm长为半径画⊙C,则⊙C与AB的位置关系怎样?
(2)若要使AB与⊙C 相切,则⊙C的半径应当是多少?
(3)若要以AC为直径画⊙O,则⊙O与AB、BC的位置关系分别怎样?
课堂检测
解:过C作CD⊥AB,垂足为D .
因为BC2+AC2=62+82=100,AB2=102=100,
所以BC2+AC2= AB2,故△ABC是直角三角形,根据三角形面积相等得:
(1)若以C为圆心,4cm长为半径画⊙C ,因为4cm<4.8cm,所以⊙C与AB的位置关系为相离.
(2)若要使AB与⊙C相切,则⊙C的半径应为4.8cm .
(3)若以AC为直径画⊙O,由于BC⊥AC,故⊙O与BC相切;⊙O与AB相交.
课堂检测
如图,PA、PB是⊙O的切线,切点分别是点A、B,直线EF也是⊙O的切线,切点为点Q,分别交PA、PB于点F、E.已知PA=12 cm,求△PEF的周长。
课堂检测
分析:根据切线长定理,得PA=PB,EB=EQ,FQ=FA,从而可将求△PEF的周长转化为求2PA的值.
解答:∵PA、PB是⊙O的切线,
∴PA=PB.
又∵直线EF是⊙O的切线,
∴EB=EQ,FQ=FA,
∴△PEF的周长=PE+PF+EF=PE+PF+EB+FA=PA+PB=2PA=24cm.
课堂检测
如图,在△ABC中,∠A=66°,点I是内心,则∠BIC的大小为( )
C
课堂检测
C
课堂检测
B
课堂检测
如图是油路管道的一部分,延伸外围的支路恰好构成一个直角三角形,两直角边分别为3 m和4 m.按照输油中心O到三条支路的距离相等来连接管道,则O到三条支路的管道总长(计算时视管道为线,中心O为点)是( )
B
课堂检测
.O
特点:直线和圆没有公共点,叫做直线和圆相离。
.O
特点:直线和圆有唯一的公共点,叫做直线和圆相切.这时的直线叫切线, 唯一的公共点叫切点。
.O
特点:直线和圆有两个公共点,叫做直线和圆相交,这时的直线叫做圆的割线。
1.直线与圆的位置关系(图形特征----用公共点的个数来区分)。
.A
.A
.B
切点
课堂小结
切线长和切线长定理:
经过圆外一点的圆的切线上,这点和切点之间线段的长,叫做这点到圆的切线长。
切线长定理:
从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分这两条切线的夹角。
核心提示:
(1)从圆外任意一点都可以引圆的两条切线,过圆上一点只能引圆的一条切线。
(2)切线长定理主要用于证明线段相等、角相等及垂直关系。
课堂小结
人教版九年级数学上册
谢 谢
同课章节目录
