24.3.1 正多边形与圆 课件(共24张PPT)
文档属性
| 名称 | 24.3.1 正多边形与圆 课件(共24张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 630.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-26 18:41:03 | ||
图片预览




文档简介
(共24张PPT)
第二十四章 圆
24.3.1
正多边形与圆(第1课时)
人教版九年级数学上册
导入新知
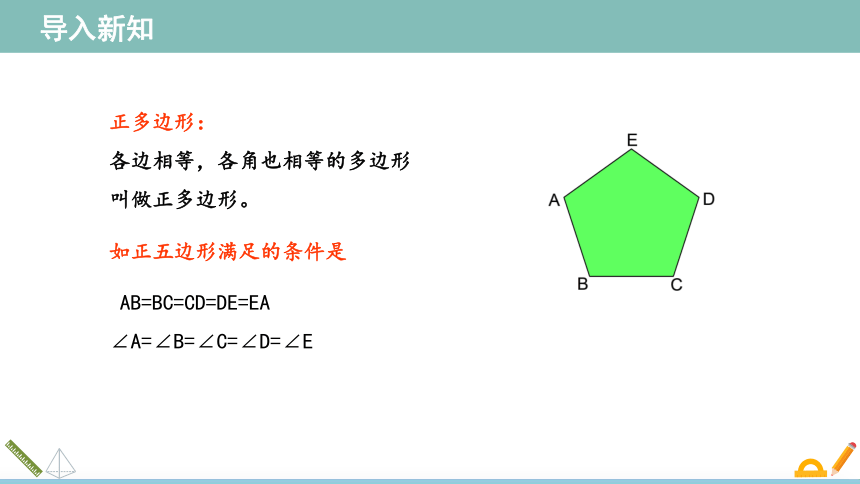
正多边形:
各边相等,各角也相等的多边形叫做正多边形。
AB=BC=CD=DE=EA
∠A=∠B=∠C=∠D=∠E
如正五边形满足的条件是
导入新知
1.了解正多边形的中心、半径、边心距、中心角等概念。
2.能运用正多边形的知识解决圆的有关计算问题。
重点难点
1.认识多边形、正多边形、圆、扇形等有关概念。(重点)
2.能根据扇形和圆的关系求扇形的圆心角的度数。(难点)
学习素养
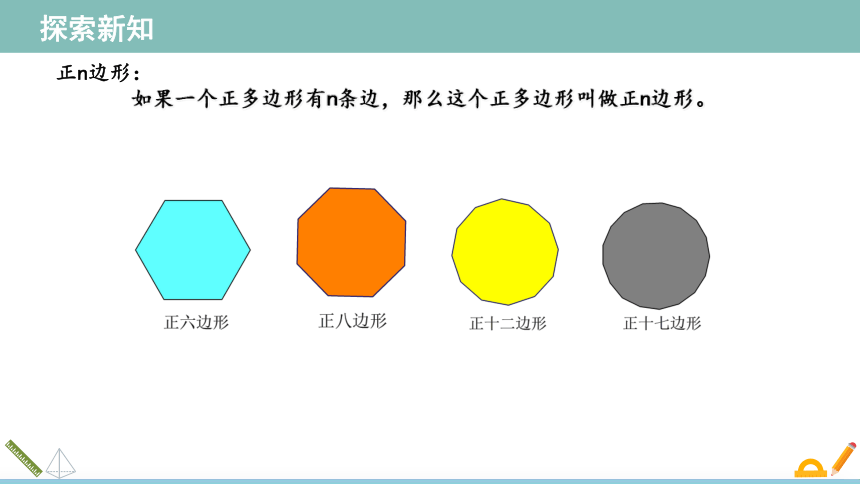
正n边形:
如果一个正多边形有n条边,那么这个正多边形叫做正n边形。
探索新知
由若干条不在同一直线上的线段首尾顺次相接组成的封闭平面图形叫做多边形。
组成多边形的各条线段叫做多边形的边。
每相邻两条边的公共端点叫做多边形的顶点。
在多边形中,连接不相邻两个顶点的线段叫做多边形的对角线。
提示:
我们平常所说的多边形都是指凸多边形,即多边形总在任何一条边所在直线的同一侧。
探索新知
想一想:菱形是正多边形吗?矩形和正方形 呢 为什么?
探索新知
你知道正多边形和圆有什么关系吗?
探索新知
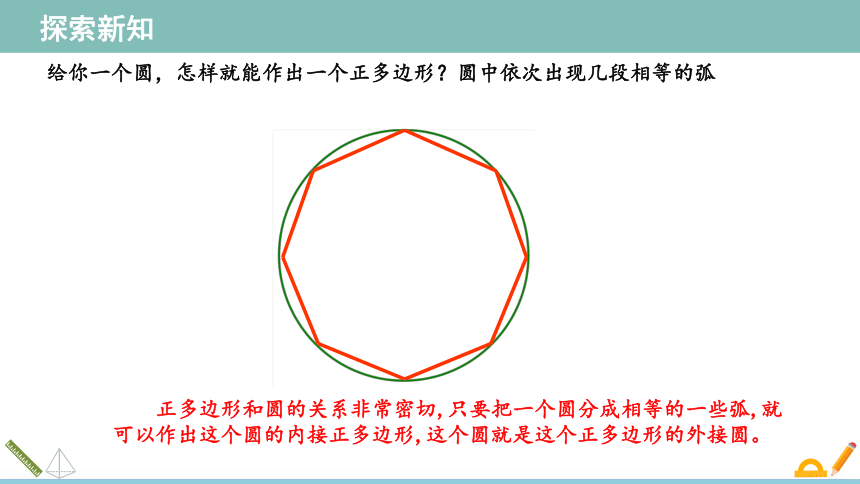
给你一个圆,怎样就能作出一个正多边形?圆中依次出现几段相等的弧
正多边形和圆的关系非常密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆。
探索新知
如图,把⊙O分成把⊙O分成相等的5段弧,依次连接各分点得到正五边形ABCDE.
∴ ∠A=∠B.
·
A
B
C
D
E
O
同理∠B=∠C=∠D=∠E.
又五边形ABCDE的顶点都在⊙O上,
∴ 五边形ABCD是⊙O的内接正五边形, ⊙O是五边形ABCD的外接圆.
我们以圆内接正五边形为例证明.
探索新知
⌒
⌒
⌒
1
2
3
A
B
C
D
E
4
⌒
⌒
5
如果将圆n等分,依次连接各分点得到一个n边形,这个n边形一定是正n边形
弦相等(多边形的边相等)
弧相等— 圆周角相等(多边形的角相等)
多边形是正多边形
探索新知
各边相等的圆内接多边形是正多边形 各角都相等的圆内接多边形呢 如果是,说明为什么;如果不是,举出反例。
解:各边相等的圆内接多边形是正多边形。
·
A1
A2
A3
A4
A5
A6
A7
An
O
先说A1
探索新知
正多边形每一边所对的圆心角叫做正多边形的中心角。
O
·
中心角
半径R
边心距r
我们把一个正多边形的外接圆的圆心叫做这个正多边形的中心。
外接圆的半径叫做正多边形的半径。
中心到正多边形的距离叫做正多边形的边心距。
探索新知
我们在以前学过了那些正多边形?
请同学们找出它们的中心,画出它们的半径,边心距和中心角!
(等边三角形,正方形等)
探索新知
E
F
C
D
.
.
O
中心角
A
B
G
边心距把△AOB分成2个全等的直角三角形
设正多边形的边长为a,半径为R,它的周长为L=na.
R
a
探索新知
有一个亭子,它的地基半径为4m的正六边形,求地基的周长和面积(精确到0.1m2).
解: 如图由于ABCDEF是正六边形,所以它的中心角等于 ,△OBC是等边三角形,从而正六边形的边长等于它的半径.
因此,亭子地基的周长
l =4×6=24(m).
在Rt△OPC中,OC=4,PC=
利用勾股定理,可得边心距
亭子地基的面积
O
A
B
C
D
E
F
R
P
r
课堂练习
请同学们完成下表中有关正多边形的计算
正多边形边数 内角 中心角 半径 边长 边心距 周长 面积
3
4
6
1
60°
90°
120°
120°
90°
60°
2
4
2
2
12
8
2
1
课堂练习
下列说法正确的是( )
A.由不在同一直线上的几条线段相连所组成的封闭图形叫做多边形
B.一条弧和经过弧的两条半径围成的图形叫做扇形
C.三角形是最简单的多边形
D.扇形是圆的一部分
C
课堂练习
刘师傅把一个四边形的木板锯掉一个角,那么剩下的木板的形状不可能是( )
A.三角形 B.四边形
C.五边形 D.六边形
D
课堂练习
将一个圆分割成四个扇形,它们圆心角的度数之比为1∶2∶3∶4,则这四个扇形的圆心角的度数依次为________,________,________,________.
36° 72° 108° 144°
课堂练习
如图,把一个圆分成四个扇形,若该圆的半径为4 cm,你能求出它们的面积吗?
解:因为圆的面积为:π×42=16π(cm2).
所以S扇形OAB=16π×45%=7.2π(cm2);
S扇形OBC=16π×10%=1.6π(cm2);
S扇形OCD=16π×25%=4π(cm2);
S扇形OAD=16π×30%=4.8π(cm2).
课堂练习
课堂小结
多边形和圆的初步认识
多边形
圆
多边形的对角线
正多边形
圆心角
扇形面积
n边形的对角线
分割三角形
1.定义判定:证明多边形的各边相等,各角相等。
2.正多边形与圆的关系判定:多边形为圆内接多边形时,判断该多边形的顶点将圆等分即可。
3.与正n边形有关的角。
(1)中心角:每一个中心角度数为:
(2)内角:每个内角度数为:
(3)外角:每个外角的度数为:
课堂小结
人教版九年级数学上册
谢 谢
第二十四章 圆
24.3.1
正多边形与圆(第1课时)
人教版九年级数学上册
导入新知
正多边形:
各边相等,各角也相等的多边形叫做正多边形。
AB=BC=CD=DE=EA
∠A=∠B=∠C=∠D=∠E
如正五边形满足的条件是
导入新知
1.了解正多边形的中心、半径、边心距、中心角等概念。
2.能运用正多边形的知识解决圆的有关计算问题。
重点难点
1.认识多边形、正多边形、圆、扇形等有关概念。(重点)
2.能根据扇形和圆的关系求扇形的圆心角的度数。(难点)
学习素养
正n边形:
如果一个正多边形有n条边,那么这个正多边形叫做正n边形。
探索新知
由若干条不在同一直线上的线段首尾顺次相接组成的封闭平面图形叫做多边形。
组成多边形的各条线段叫做多边形的边。
每相邻两条边的公共端点叫做多边形的顶点。
在多边形中,连接不相邻两个顶点的线段叫做多边形的对角线。
提示:
我们平常所说的多边形都是指凸多边形,即多边形总在任何一条边所在直线的同一侧。
探索新知
想一想:菱形是正多边形吗?矩形和正方形 呢 为什么?
探索新知
你知道正多边形和圆有什么关系吗?
探索新知
给你一个圆,怎样就能作出一个正多边形?圆中依次出现几段相等的弧
正多边形和圆的关系非常密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆。
探索新知
如图,把⊙O分成把⊙O分成相等的5段弧,依次连接各分点得到正五边形ABCDE.
∴ ∠A=∠B.
·
A
B
C
D
E
O
同理∠B=∠C=∠D=∠E.
又五边形ABCDE的顶点都在⊙O上,
∴ 五边形ABCD是⊙O的内接正五边形, ⊙O是五边形ABCD的外接圆.
我们以圆内接正五边形为例证明.
探索新知
⌒
⌒
⌒
1
2
3
A
B
C
D
E
4
⌒
⌒
5
如果将圆n等分,依次连接各分点得到一个n边形,这个n边形一定是正n边形
弦相等(多边形的边相等)
弧相等— 圆周角相等(多边形的角相等)
多边形是正多边形
探索新知
各边相等的圆内接多边形是正多边形 各角都相等的圆内接多边形呢 如果是,说明为什么;如果不是,举出反例。
解:各边相等的圆内接多边形是正多边形。
·
A1
A2
A3
A4
A5
A6
A7
An
O
先说A1
探索新知
正多边形每一边所对的圆心角叫做正多边形的中心角。
O
·
中心角
半径R
边心距r
我们把一个正多边形的外接圆的圆心叫做这个正多边形的中心。
外接圆的半径叫做正多边形的半径。
中心到正多边形的距离叫做正多边形的边心距。
探索新知
我们在以前学过了那些正多边形?
请同学们找出它们的中心,画出它们的半径,边心距和中心角!
(等边三角形,正方形等)
探索新知
E
F
C
D
.
.
O
中心角
A
B
G
边心距把△AOB分成2个全等的直角三角形
设正多边形的边长为a,半径为R,它的周长为L=na.
R
a
探索新知
有一个亭子,它的地基半径为4m的正六边形,求地基的周长和面积(精确到0.1m2).
解: 如图由于ABCDEF是正六边形,所以它的中心角等于 ,△OBC是等边三角形,从而正六边形的边长等于它的半径.
因此,亭子地基的周长
l =4×6=24(m).
在Rt△OPC中,OC=4,PC=
利用勾股定理,可得边心距
亭子地基的面积
O
A
B
C
D
E
F
R
P
r
课堂练习
请同学们完成下表中有关正多边形的计算
正多边形边数 内角 中心角 半径 边长 边心距 周长 面积
3
4
6
1
60°
90°
120°
120°
90°
60°
2
4
2
2
12
8
2
1
课堂练习
下列说法正确的是( )
A.由不在同一直线上的几条线段相连所组成的封闭图形叫做多边形
B.一条弧和经过弧的两条半径围成的图形叫做扇形
C.三角形是最简单的多边形
D.扇形是圆的一部分
C
课堂练习
刘师傅把一个四边形的木板锯掉一个角,那么剩下的木板的形状不可能是( )
A.三角形 B.四边形
C.五边形 D.六边形
D
课堂练习
将一个圆分割成四个扇形,它们圆心角的度数之比为1∶2∶3∶4,则这四个扇形的圆心角的度数依次为________,________,________,________.
36° 72° 108° 144°
课堂练习
如图,把一个圆分成四个扇形,若该圆的半径为4 cm,你能求出它们的面积吗?
解:因为圆的面积为:π×42=16π(cm2).
所以S扇形OAB=16π×45%=7.2π(cm2);
S扇形OBC=16π×10%=1.6π(cm2);
S扇形OCD=16π×25%=4π(cm2);
S扇形OAD=16π×30%=4.8π(cm2).
课堂练习
课堂小结
多边形和圆的初步认识
多边形
圆
多边形的对角线
正多边形
圆心角
扇形面积
n边形的对角线
分割三角形
1.定义判定:证明多边形的各边相等,各角相等。
2.正多边形与圆的关系判定:多边形为圆内接多边形时,判断该多边形的顶点将圆等分即可。
3.与正n边形有关的角。
(1)中心角:每一个中心角度数为:
(2)内角:每个内角度数为:
(3)外角:每个外角的度数为:
课堂小结
人教版九年级数学上册
谢 谢
同课章节目录
