24.3.2 正多边形与圆 课件(共23张PPT)
文档属性
| 名称 | 24.3.2 正多边形与圆 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 895.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-26 18:42:13 | ||
图片预览






文档简介
(共23张PPT)
第二十四章 圆
24.3.2
正多边形与圆(第2课时)
人教版九年级数学上册
1.通过正多边形的概念,能通过等分圆心角的方法等分圆周画出所需的正多边形。
2.会判定一个正多边形是中心对称图形还是轴对称图形,能够用直尺和圆规作图,作出一些特殊的正多边形。
3.会进行有关圆与正多边形的计算。
重点难点
重点:正多边形和圆中正多边形半径、中心角、弦心距、边长之间的关系。
难点:理解正多边形半径、中心角、弦心距、边长之间的关系。
学习素养
各边相等,各角也相等的多边形是正多边形.
正n 边形:如果一个正多边形有n 条边,
那么这个正多边形叫做正n 边形.
三条边相等,三个角相等(60°)
四条边相等,四个角相等(90°)
正三角形
正方形
正多边形定义
探索新知
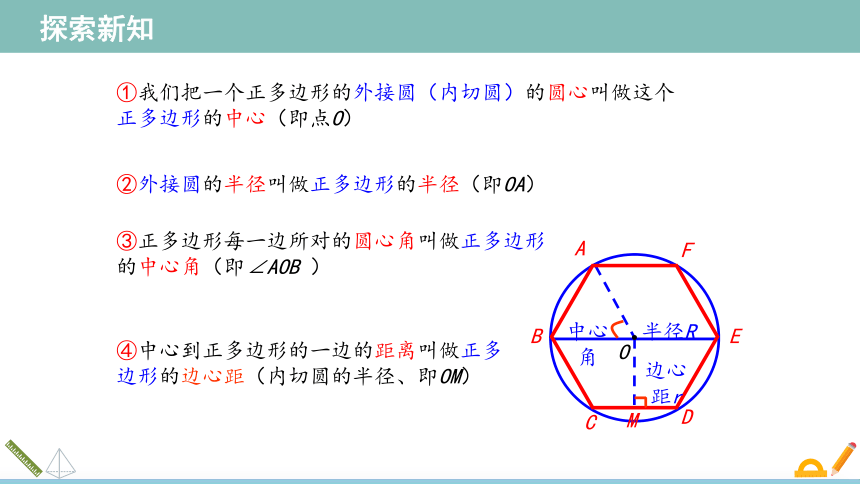
③正多边形每一边所对的圆心角叫做正多边形的中心角(即∠AOB )
①我们把一个正多边形的外接圆(内切圆)的圆心叫做这个正多边形的中心(即点O)
②外接圆的半径叫做正多边形的半径(即OA)
④中心到正多边形的一边的距离叫做正多边形的边心距(内切圆的半径、即OM)
O
·
中心角
半径R
边心距r
A
B
C
D
E
F
M
探索新知
如图,正六边形ABCDEF的半径为2,以它的中心O为坐标原点,顶点B、E在x轴上,求正六边形ABCDEF的各顶点的坐标.
A(-1, )
B(-2,0 )
C(-1, )
D(1, )
E(2,0 )
F( 1, )
探索新知
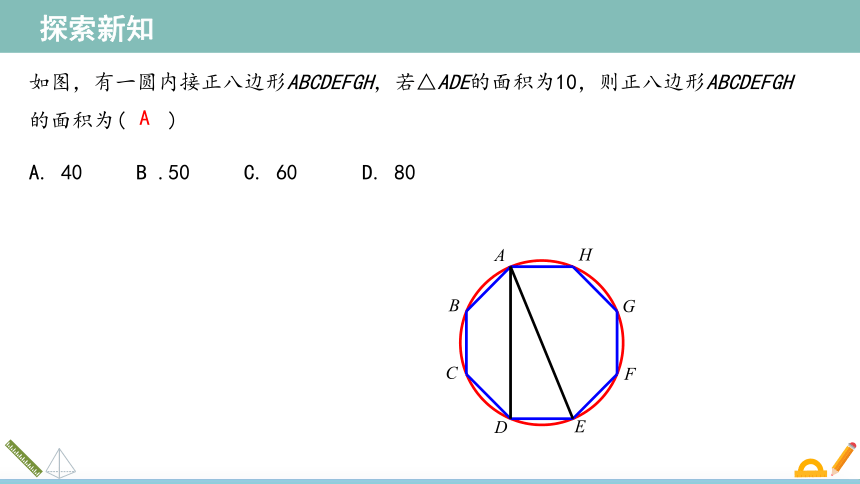
如图,有一圆内接正八边形ABCDEFGH,若△ADE的面积为10,则正八边形ABCDEFGH的面积为( )
A. 40 B .50 C. 60 D. 80
B
A
C
D
E
F
G
H
A
探索新知
正多边形的画法
用量角器等分圆,再作正多边形 在半径为R的圆中,先用量角器画一个等于
的圆心角,这个角所对的弧就是圆周的 ,然后在圆上依次截取这条弧的等弧,就得到圆的n等分点,依次连接各分点,从而作出半径为R的正n边形
用尺规等分圆,再作正多边形 在⊙O中用直尺和圆规作两条互相垂直的直径,就可以把⊙O四等分,从而作出正方形;再次平分正方形的每组对边,就可以作出正八边形……
探索新知
(1)画正多边形的原理:在同圆中,相等的圆心角所对的弧相等.
(2)用量角器等分圆是一种简单而常用的方法.但边数很多时,容易有较大的误差.
(3)尺规作图是一种比较准确的等分圆的方法,但有很大的局限性,它不能将圆任意等分,只限于一些特殊的正多边形,如正方形、正八边形、正十六边形,正三角形、正六边形、正十二边形等
探索新知
正多边形的有关计算
探索新知
正多边形和圆
只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.
注意:任何正多边形都有一个外接圆和一个内切圆,而且这两个圆是同心圆.
探索新知
探索新知
画正n边形的方法和步骤
(1)将一个圆n等分;
(2)顺次连接各等分点.
探索新知
用尺规作正多边形
对于一些特殊的多边形,还可以用圆规和直尺来作.如正三角形、正方形、正六边形、正八边形及正十二边形等.
注意:不是任意一个正多边形都可以利用尺规作图作出,利用尺规作图只能作出一些特殊的正多边形,如边数是3或4的偶数倍的正多边形,可以利用尺规作图作出.
探索新知
如图,正八边形 ABCDEFGH的半径为2,求它的面积.
课堂练习
A
课堂练习
B
课堂练习
A
课堂练习
8
课堂练习
课堂练习6°或114°
课堂练习
A
课堂练习
正多边形:各边相等、各角相等的多边形是正多边形.
正多边形与圆的关系:把圆分成n(n≥3)等份,顺次连接各分点所得的多边形是这个圆的内接正n边形。
正多边形的中心:正多边形的外接圆的圆心叫做正多边形的中心.
正多边形的半径:外接圆的半径叫做正多边形的半径.
正多边形的中心角:正多边形每一边所对的圆心角叫做正多边形的中心角.正n边形的每个中心角都等于 .
正多边形的边心距:中心到正多边形的一边的距离叫做正多边形的边心距.
课堂小结
人教版九年级数学上册
谢 谢
第二十四章 圆
24.3.2
正多边形与圆(第2课时)
人教版九年级数学上册
1.通过正多边形的概念,能通过等分圆心角的方法等分圆周画出所需的正多边形。
2.会判定一个正多边形是中心对称图形还是轴对称图形,能够用直尺和圆规作图,作出一些特殊的正多边形。
3.会进行有关圆与正多边形的计算。
重点难点
重点:正多边形和圆中正多边形半径、中心角、弦心距、边长之间的关系。
难点:理解正多边形半径、中心角、弦心距、边长之间的关系。
学习素养
各边相等,各角也相等的多边形是正多边形.
正n 边形:如果一个正多边形有n 条边,
那么这个正多边形叫做正n 边形.
三条边相等,三个角相等(60°)
四条边相等,四个角相等(90°)
正三角形
正方形
正多边形定义
探索新知
③正多边形每一边所对的圆心角叫做正多边形的中心角(即∠AOB )
①我们把一个正多边形的外接圆(内切圆)的圆心叫做这个正多边形的中心(即点O)
②外接圆的半径叫做正多边形的半径(即OA)
④中心到正多边形的一边的距离叫做正多边形的边心距(内切圆的半径、即OM)
O
·
中心角
半径R
边心距r
A
B
C
D
E
F
M
探索新知
如图,正六边形ABCDEF的半径为2,以它的中心O为坐标原点,顶点B、E在x轴上,求正六边形ABCDEF的各顶点的坐标.
A(-1, )
B(-2,0 )
C(-1, )
D(1, )
E(2,0 )
F( 1, )
探索新知
如图,有一圆内接正八边形ABCDEFGH,若△ADE的面积为10,则正八边形ABCDEFGH的面积为( )
A. 40 B .50 C. 60 D. 80
B
A
C
D
E
F
G
H
A
探索新知
正多边形的画法
用量角器等分圆,再作正多边形 在半径为R的圆中,先用量角器画一个等于
的圆心角,这个角所对的弧就是圆周的 ,然后在圆上依次截取这条弧的等弧,就得到圆的n等分点,依次连接各分点,从而作出半径为R的正n边形
用尺规等分圆,再作正多边形 在⊙O中用直尺和圆规作两条互相垂直的直径,就可以把⊙O四等分,从而作出正方形;再次平分正方形的每组对边,就可以作出正八边形……
探索新知
(1)画正多边形的原理:在同圆中,相等的圆心角所对的弧相等.
(2)用量角器等分圆是一种简单而常用的方法.但边数很多时,容易有较大的误差.
(3)尺规作图是一种比较准确的等分圆的方法,但有很大的局限性,它不能将圆任意等分,只限于一些特殊的正多边形,如正方形、正八边形、正十六边形,正三角形、正六边形、正十二边形等
探索新知
正多边形的有关计算
探索新知
正多边形和圆
只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.
注意:任何正多边形都有一个外接圆和一个内切圆,而且这两个圆是同心圆.
探索新知
探索新知
画正n边形的方法和步骤
(1)将一个圆n等分;
(2)顺次连接各等分点.
探索新知
用尺规作正多边形
对于一些特殊的多边形,还可以用圆规和直尺来作.如正三角形、正方形、正六边形、正八边形及正十二边形等.
注意:不是任意一个正多边形都可以利用尺规作图作出,利用尺规作图只能作出一些特殊的正多边形,如边数是3或4的偶数倍的正多边形,可以利用尺规作图作出.
探索新知
如图,正八边形 ABCDEFGH的半径为2,求它的面积.
课堂练习
A
课堂练习
B
课堂练习
A
课堂练习
8
课堂练习
课堂练习6°或114°
课堂练习
A
课堂练习
正多边形:各边相等、各角相等的多边形是正多边形.
正多边形与圆的关系:把圆分成n(n≥3)等份,顺次连接各分点所得的多边形是这个圆的内接正n边形。
正多边形的中心:正多边形的外接圆的圆心叫做正多边形的中心.
正多边形的半径:外接圆的半径叫做正多边形的半径.
正多边形的中心角:正多边形每一边所对的圆心角叫做正多边形的中心角.正n边形的每个中心角都等于 .
正多边形的边心距:中心到正多边形的一边的距离叫做正多边形的边心距.
课堂小结
人教版九年级数学上册
谢 谢
同课章节目录
