25.2.1 用列举法求概率 课件(共36张PPT)
文档属性
| 名称 | 25.2.1 用列举法求概率 课件(共36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-26 18:49:28 | ||
图片预览











文档简介
(共36张PPT)
人教版九年级数学上册
25.2.1 用列举法求概率(第1课时)
导入新知
篮球比赛中,裁判员一般是通过掷硬币决定哪个队先发球,这样的游戏公平吗?为什么?
小颖为一节活动课设计了一个“配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分成相等的几个扇形.游戏规则是:游戏者同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,那么他就赢了,因为红色和蓝色在一起配成了紫色。问:游戏者获胜的概率是多少?
导入新知
老师向空中抛掷两枚同样的一元硬币,如果落地后一正一反,老师赢;如果落地后两面一样,你们赢.请问,你们觉得这个游戏公平吗?
上边的问题有几种可能呢?怎样才能不重不漏地列举所有可能出现的结果呢?
导入新知
素养目标
3. 知道如何利用“列表法”求随机事件的概率.
1. 会用直接列举法和列表法列举所有可能出现的结果.
2. 会用列表法求出事件的概率.
同时掷两枚硬币,试求下列事件的概率:
(1)两枚两面一样;
(2)一枚硬币正面朝上,一枚硬币反面朝上;
①
②
用直接列举法求概率
知识点 1
探索新知
“掷两枚硬币”所有结果如下:
正正
正反
反正
反反
①
②
①
②
①
②
①
②
探索新知
解:
(1)两枚硬币两面一样包括两面都是正面、两面都是反面,共两种情形,其概率为 ;
(2)一枚硬币正面朝上,一枚硬币反面朝上,共有反正、正反两种情形,其概率为
探索新知
上述这种列举法我们称为直接列举法,即把事件可能出现的结果一一列出.
【注意】直接列举法比较适合用于最多涉及两个试验因素或分两步进行的试验,且事件总结果的种数比较少的等可能性事件.
探索新知
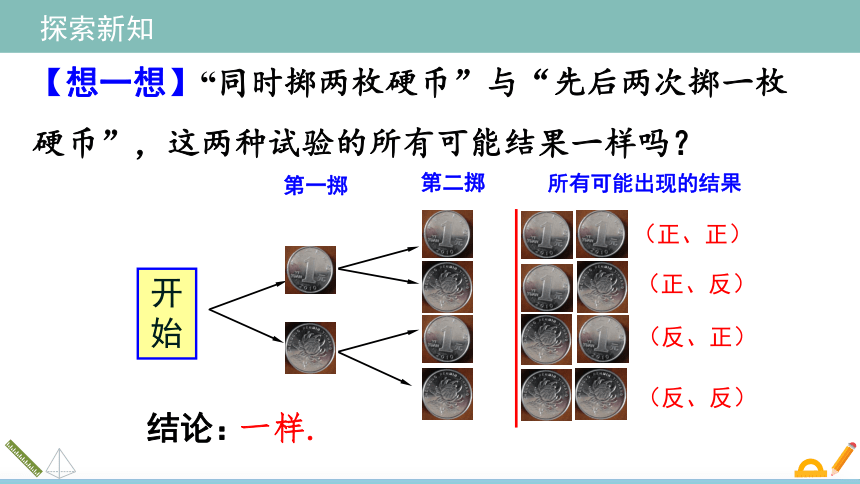
【想一想】“同时掷两枚硬币”与“先后两次掷一枚硬币”,这两种试验的所有可能结果一样吗?
开始
第一掷
第二掷
所有可能出现的结果
(正、正)
(正、反)
(反、正)
(反、反)
结论:
一样.
探索新知
随机事件“同时”与“先后”的关系:“两个相同的随机事件同时发生”与 “一个随机事件先后两次发生”的结果是一样的.
探索新知
同时掷两枚硬币,试求下列事件的概率:
(1)两枚两面一样;
(2)一枚硬币正面朝上,一枚硬币反面朝上;
用列表法求概率
知识点 2
还有别的方法求上述事件的概率吗?
探索新知
第1枚硬币
第
2
枚硬币
反
正
正
正
正
反
反
反
反
反
正
正
正
正
正
正
反
反
反
正
探索新知
【思考】怎样列表格呢?
一个因素所包含的可能情况
另一个因素所包含的可能情况
两个因素所组合的所有可能情况,即n
列表法中表格构造特点:
说明
如果第一个因素包含2种情况;第二个因素包含3种情况;那么所有情况n=2×3=6.
探索新知
例1 同时掷两个质地均匀的骰子,计算下列事件的概率:
(1)两个骰子的点数相同.
(2)两个骰子的点数之和
是9.
(3)至少有一个骰子的点数
为2.
第
一
个
第
二
个
1 2 3 4 5 6
1
2
3
4
5
6
利用列表法解答掷骰子问题
素养考点 1
探索新知
1 2 3 4 5 6
1
2
3
4
5
6
第
一
个
第
二
个
(1,1) (2,1) (3,1) (4,1) (5,1) (6,1)
(1,2) (2,2) (3,2) (4,2) (5,2) (6,2)
(1,3) (2,3) (3,3) (4,3) (5,3) (6,3)
(1,4) (2,4) (3,4) (4,4) (5,4) (6,4)
(1,5) (2,5) (3,5) (4,5) (5,5) (6,5)
(1,6) (2,6) (3,6) (4,6) (5,6) (6,6)
分析:首先要弄清楚一共有多少个可能结果.第1枚骰子可能掷出1、2、···6中的每一种情况,第2枚骰子也可能掷出1,2,···,6中的每一种情况.可以用“列表法”列出所有可能的结果如下:
探索新知
解:由列表得,同时掷两个骰子,可能出现的结果有36个,它们出现的可能性相等.
(1)满足两个骰子的点数相同(记为事件A)的结果有6个,则P(A)= .
(2)满足两个骰子的点数之和是9(记为事件B)的结果有4个,则P(B)= .
(3)满足至少有一个骰子的点数为2(记为事件C)的结果有11个,则P(C)= .
探索新知
当一次试验要涉及两个因素(例如掷两个骰子)并且可能出现的结果数目较多时,为不重不漏地列出所有可能结果,通常采用列表法.
探索新知
同时抛掷2枚均匀的骰子一次,骰子各面上的点数分别是1、2、3···6.试分别计算如下各随机事件的概率.
(1)抛出的点数之和等于8;
(2)抛出的点数之和等于12.
分析:首先要弄清楚一共有多少个可能结果.第1枚骰子可能掷出1、2、···6中的每一种情况,第2枚骰子也可能掷出1、2、···6中的每一种情况.可以用“列表法”列出所有可能的结果.
课堂练习
第2枚
骰子
第1枚
骰子
结
果
1
2
3
4
5
6
1
2
3
4
5
6
(1,1)
(1,2)
(1,3)
(1,4)
(1,5)
(1,6)
(2,1)
(3,1)
(4,1)
(5,1)
(6,1)
(2,2)
(2,3)
(2,4)
(2,5)
(2,6)
(3,2)
(3,3)
(3,4)
(3,5)
(3,6)
(4,2)
(5,2)
(6,2)
(4,3)
(5,3)
(6,3)
(4,4)
(5,4)
(6,4)
(4,5)
(5,5)
(6,5)
(4,6)
(5,6)
(6,6)
课堂练习
解:从上表可以看出,同时抛掷两枚骰子一次,所有可能出现的结果有36种.由于骰子是均匀的,所以每个结果出现的可能性相等.
(1)抛出点数之和等于8的结果(2,6),(3,5),(4,4),(5,3)和(6,2)这5种,所以抛出的点数之和等于8的这个事件发生的概率为 ;
(2)抛出点数之和等于12的结果仅有(6,6)这1种,所以抛出的点数之和等于12的这个事件发生的概率为 .
课堂练习
例2 一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出一个球,记录下颜色后放回袋中并搅匀,
再从中任意摸出一个球,两次都摸
出红球的概率是多少?
1
2
利用列表法计算摸球游戏的概率
素养考点 2
探索新知
结果
第一次
第二次
解:利用表格列出所有可能的结果:
白
红1
红2
白
红1
红2
(白,白)
(白,红1)
(白,红2)
(红1,白)
(红1,红1)
(红1,红2)
(红2,白)
(红2,红1)
(红2,红2)
课堂练习
一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出一个球,记录下颜色后不再放回袋中,再从中任意摸出一个球,两次都摸出红球的概率是多少?
解:利用表格列出所有可能的结果:
白
红1
红2
白
红1
红2
(白,红1)
(白,红2)
(红1,白)
(红1,红2)
(红2,白)
(红2,红1)
结果
第一次
第二次
探究新知
通过例2及拓展延伸的讲解,放回与不放回列举的过程是不同的,解答问题时,注意明确,若无明确,具体问题具体分析.
注 意
课堂练习
如图,袋中装有两个完全相同的球,分别标有数字“1”和“2”.小明设计了一个游戏:游戏者每次从袋中随机摸出一个球,并自由转动图中的转盘(转盘被分成相等的三个扇形).
游戏规则是:如果所摸球上的数字与转盘转出的数字之和为2,那么游戏者获胜.求游戏者获胜的概率.
1
2
3
课堂练习
解:每次游戏时,所有可能出现的结果如下:
总共有6种结果,每种结果出现的可能性相同,而所摸球上的数字与转盘转出的数字之和为2的结果只有一种:(1,1),因此游戏者获胜的概率为 .
转盘 摸球
1
1
2
(1,1)
(1,2)
2
(2,1)
(2,2)
3
(1,3)
(2,3)
1
2
3
课堂练习
例3 甲乙两人要去风景区游玩,仅知道每天开往风景区有3辆汽车,并且舒适程度分别为上等、中等、下等3种,当不知道怎样区分这些车,也不知道它们会以怎样的顺序开来.于是他们分别采用了不同的乘车办法:甲乘第1辆开来的车.乙不乘第1辆车,并且仔细观察第2辆车的情况,如果比第1辆车好就乘坐,比第1辆车差就乘第3辆车.试问甲、乙两人的乘车办法,哪一种更有利于乘上舒适程度上等的车?
利用列表法求简单生活问题的概率
素养考点 3
探究新知
解:容易知道3辆汽车开来的先后顺序有如下6种可能情况:
(上中下),
(上下中),
(中上下),
(中下上),
(下上中),
(下中上).
假定6种顺序出现的可能性相等, 在各种可能顺序之下,甲乙两人分别会乘坐的汽车列表如下:
顺序 甲 乙
上中下
上下中
中上下
中下上
下上中
下中上
上
下
上
中
中
上
中
上
下
上
下
中
甲乘到上等、中等、下等3种汽车的概率都是 ;
乙乘坐到上等汽车的概率是 ,乘坐到下等汽车的概率只有 .
答:乙的乘车办法有有利于乘上舒适度较好的车.
课堂练习
小明和小亮做扑克游戏,桌面上放有两堆牌,分别是红桃和黑桃的1、2、3、4、5、6,小明建议:“我从红桃中抽取一张牌,你从黑桃中取一张,当两张牌数字之积为奇数时,你得1分,为偶数我得1分,先得到10分的获胜.”如果你是小亮,你愿意接受这个游戏的规则吗
你能求出小亮得分的概率吗
课堂练习
这个游戏对小亮和小明公平吗?
1 2 3 4 5 6
1 (1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
2 (2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
3 (3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
4 (4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
5 (5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
6 (6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
红桃
黑桃
分析:用表格表示
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
课堂练习
解:由表中可以看出,在两堆牌中分别取一张,它可能出现的结果有36个,它们出现的可能性相等.
满足两张牌的数字之积为奇数(记为事件A)的有
(1,1)(1,3)(1,5)(3,1)(3,3)(3,5)(5,1)(5,3)(5,5)这9种情况,所以
P(A)= =
课堂练习
一个不透明的口袋中有三个小球,上面分别标有字母A,B,C,除所标字母不同外,其它完全相同,从中随机摸出一个小球,记下字母后放回并搅匀,再随机摸出一个小球,用列表的方法,求该同学两次摸出的小球所标字母相同的概率.
课堂练习
解:列表得
由列表可知可能出现的结果共9种,其中两次摸出的小球所标字母相同的情况数有3种.所以该同学两次摸出的小球所标字母相同的概率= = .
A B C
A (A,A) (B,A) (C,A)
B (A,B) (B,B) (C,B)
C (A,C) (B,C) (C,C)
课堂练习
列举法
关键
常用
方法
直接列举法
列表法
适用对象
两个试验因素或分两步进行的试验
基本步骤
列表;确定m、n值代入概率公式计算
在于正确列举出试验结果的各种可能性.
确保试验中每种结果出现的可能性大小相等
前提条件
课堂小结
谢 谢
人教版九年级数学上册
25.2.1 用列举法求概率(第1课时)
导入新知
篮球比赛中,裁判员一般是通过掷硬币决定哪个队先发球,这样的游戏公平吗?为什么?
小颖为一节活动课设计了一个“配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分成相等的几个扇形.游戏规则是:游戏者同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,那么他就赢了,因为红色和蓝色在一起配成了紫色。问:游戏者获胜的概率是多少?
导入新知
老师向空中抛掷两枚同样的一元硬币,如果落地后一正一反,老师赢;如果落地后两面一样,你们赢.请问,你们觉得这个游戏公平吗?
上边的问题有几种可能呢?怎样才能不重不漏地列举所有可能出现的结果呢?
导入新知
素养目标
3. 知道如何利用“列表法”求随机事件的概率.
1. 会用直接列举法和列表法列举所有可能出现的结果.
2. 会用列表法求出事件的概率.
同时掷两枚硬币,试求下列事件的概率:
(1)两枚两面一样;
(2)一枚硬币正面朝上,一枚硬币反面朝上;
①
②
用直接列举法求概率
知识点 1
探索新知
“掷两枚硬币”所有结果如下:
正正
正反
反正
反反
①
②
①
②
①
②
①
②
探索新知
解:
(1)两枚硬币两面一样包括两面都是正面、两面都是反面,共两种情形,其概率为 ;
(2)一枚硬币正面朝上,一枚硬币反面朝上,共有反正、正反两种情形,其概率为
探索新知
上述这种列举法我们称为直接列举法,即把事件可能出现的结果一一列出.
【注意】直接列举法比较适合用于最多涉及两个试验因素或分两步进行的试验,且事件总结果的种数比较少的等可能性事件.
探索新知
【想一想】“同时掷两枚硬币”与“先后两次掷一枚硬币”,这两种试验的所有可能结果一样吗?
开始
第一掷
第二掷
所有可能出现的结果
(正、正)
(正、反)
(反、正)
(反、反)
结论:
一样.
探索新知
随机事件“同时”与“先后”的关系:“两个相同的随机事件同时发生”与 “一个随机事件先后两次发生”的结果是一样的.
探索新知
同时掷两枚硬币,试求下列事件的概率:
(1)两枚两面一样;
(2)一枚硬币正面朝上,一枚硬币反面朝上;
用列表法求概率
知识点 2
还有别的方法求上述事件的概率吗?
探索新知
第1枚硬币
第
2
枚硬币
反
正
正
正
正
反
反
反
反
反
正
正
正
正
正
正
反
反
反
正
探索新知
【思考】怎样列表格呢?
一个因素所包含的可能情况
另一个因素所包含的可能情况
两个因素所组合的所有可能情况,即n
列表法中表格构造特点:
说明
如果第一个因素包含2种情况;第二个因素包含3种情况;那么所有情况n=2×3=6.
探索新知
例1 同时掷两个质地均匀的骰子,计算下列事件的概率:
(1)两个骰子的点数相同.
(2)两个骰子的点数之和
是9.
(3)至少有一个骰子的点数
为2.
第
一
个
第
二
个
1 2 3 4 5 6
1
2
3
4
5
6
利用列表法解答掷骰子问题
素养考点 1
探索新知
1 2 3 4 5 6
1
2
3
4
5
6
第
一
个
第
二
个
(1,1) (2,1) (3,1) (4,1) (5,1) (6,1)
(1,2) (2,2) (3,2) (4,2) (5,2) (6,2)
(1,3) (2,3) (3,3) (4,3) (5,3) (6,3)
(1,4) (2,4) (3,4) (4,4) (5,4) (6,4)
(1,5) (2,5) (3,5) (4,5) (5,5) (6,5)
(1,6) (2,6) (3,6) (4,6) (5,6) (6,6)
分析:首先要弄清楚一共有多少个可能结果.第1枚骰子可能掷出1、2、···6中的每一种情况,第2枚骰子也可能掷出1,2,···,6中的每一种情况.可以用“列表法”列出所有可能的结果如下:
探索新知
解:由列表得,同时掷两个骰子,可能出现的结果有36个,它们出现的可能性相等.
(1)满足两个骰子的点数相同(记为事件A)的结果有6个,则P(A)= .
(2)满足两个骰子的点数之和是9(记为事件B)的结果有4个,则P(B)= .
(3)满足至少有一个骰子的点数为2(记为事件C)的结果有11个,则P(C)= .
探索新知
当一次试验要涉及两个因素(例如掷两个骰子)并且可能出现的结果数目较多时,为不重不漏地列出所有可能结果,通常采用列表法.
探索新知
同时抛掷2枚均匀的骰子一次,骰子各面上的点数分别是1、2、3···6.试分别计算如下各随机事件的概率.
(1)抛出的点数之和等于8;
(2)抛出的点数之和等于12.
分析:首先要弄清楚一共有多少个可能结果.第1枚骰子可能掷出1、2、···6中的每一种情况,第2枚骰子也可能掷出1、2、···6中的每一种情况.可以用“列表法”列出所有可能的结果.
课堂练习
第2枚
骰子
第1枚
骰子
结
果
1
2
3
4
5
6
1
2
3
4
5
6
(1,1)
(1,2)
(1,3)
(1,4)
(1,5)
(1,6)
(2,1)
(3,1)
(4,1)
(5,1)
(6,1)
(2,2)
(2,3)
(2,4)
(2,5)
(2,6)
(3,2)
(3,3)
(3,4)
(3,5)
(3,6)
(4,2)
(5,2)
(6,2)
(4,3)
(5,3)
(6,3)
(4,4)
(5,4)
(6,4)
(4,5)
(5,5)
(6,5)
(4,6)
(5,6)
(6,6)
课堂练习
解:从上表可以看出,同时抛掷两枚骰子一次,所有可能出现的结果有36种.由于骰子是均匀的,所以每个结果出现的可能性相等.
(1)抛出点数之和等于8的结果(2,6),(3,5),(4,4),(5,3)和(6,2)这5种,所以抛出的点数之和等于8的这个事件发生的概率为 ;
(2)抛出点数之和等于12的结果仅有(6,6)这1种,所以抛出的点数之和等于12的这个事件发生的概率为 .
课堂练习
例2 一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出一个球,记录下颜色后放回袋中并搅匀,
再从中任意摸出一个球,两次都摸
出红球的概率是多少?
1
2
利用列表法计算摸球游戏的概率
素养考点 2
探索新知
结果
第一次
第二次
解:利用表格列出所有可能的结果:
白
红1
红2
白
红1
红2
(白,白)
(白,红1)
(白,红2)
(红1,白)
(红1,红1)
(红1,红2)
(红2,白)
(红2,红1)
(红2,红2)
课堂练习
一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出一个球,记录下颜色后不再放回袋中,再从中任意摸出一个球,两次都摸出红球的概率是多少?
解:利用表格列出所有可能的结果:
白
红1
红2
白
红1
红2
(白,红1)
(白,红2)
(红1,白)
(红1,红2)
(红2,白)
(红2,红1)
结果
第一次
第二次
探究新知
通过例2及拓展延伸的讲解,放回与不放回列举的过程是不同的,解答问题时,注意明确,若无明确,具体问题具体分析.
注 意
课堂练习
如图,袋中装有两个完全相同的球,分别标有数字“1”和“2”.小明设计了一个游戏:游戏者每次从袋中随机摸出一个球,并自由转动图中的转盘(转盘被分成相等的三个扇形).
游戏规则是:如果所摸球上的数字与转盘转出的数字之和为2,那么游戏者获胜.求游戏者获胜的概率.
1
2
3
课堂练习
解:每次游戏时,所有可能出现的结果如下:
总共有6种结果,每种结果出现的可能性相同,而所摸球上的数字与转盘转出的数字之和为2的结果只有一种:(1,1),因此游戏者获胜的概率为 .
转盘 摸球
1
1
2
(1,1)
(1,2)
2
(2,1)
(2,2)
3
(1,3)
(2,3)
1
2
3
课堂练习
例3 甲乙两人要去风景区游玩,仅知道每天开往风景区有3辆汽车,并且舒适程度分别为上等、中等、下等3种,当不知道怎样区分这些车,也不知道它们会以怎样的顺序开来.于是他们分别采用了不同的乘车办法:甲乘第1辆开来的车.乙不乘第1辆车,并且仔细观察第2辆车的情况,如果比第1辆车好就乘坐,比第1辆车差就乘第3辆车.试问甲、乙两人的乘车办法,哪一种更有利于乘上舒适程度上等的车?
利用列表法求简单生活问题的概率
素养考点 3
探究新知
解:容易知道3辆汽车开来的先后顺序有如下6种可能情况:
(上中下),
(上下中),
(中上下),
(中下上),
(下上中),
(下中上).
假定6种顺序出现的可能性相等, 在各种可能顺序之下,甲乙两人分别会乘坐的汽车列表如下:
顺序 甲 乙
上中下
上下中
中上下
中下上
下上中
下中上
上
下
上
中
中
上
中
上
下
上
下
中
甲乘到上等、中等、下等3种汽车的概率都是 ;
乙乘坐到上等汽车的概率是 ,乘坐到下等汽车的概率只有 .
答:乙的乘车办法有有利于乘上舒适度较好的车.
课堂练习
小明和小亮做扑克游戏,桌面上放有两堆牌,分别是红桃和黑桃的1、2、3、4、5、6,小明建议:“我从红桃中抽取一张牌,你从黑桃中取一张,当两张牌数字之积为奇数时,你得1分,为偶数我得1分,先得到10分的获胜.”如果你是小亮,你愿意接受这个游戏的规则吗
你能求出小亮得分的概率吗
课堂练习
这个游戏对小亮和小明公平吗?
1 2 3 4 5 6
1 (1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
2 (2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
3 (3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
4 (4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
5 (5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
6 (6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
红桃
黑桃
分析:用表格表示
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
课堂练习
解:由表中可以看出,在两堆牌中分别取一张,它可能出现的结果有36个,它们出现的可能性相等.
满足两张牌的数字之积为奇数(记为事件A)的有
(1,1)(1,3)(1,5)(3,1)(3,3)(3,5)(5,1)(5,3)(5,5)这9种情况,所以
P(A)= =
课堂练习
一个不透明的口袋中有三个小球,上面分别标有字母A,B,C,除所标字母不同外,其它完全相同,从中随机摸出一个小球,记下字母后放回并搅匀,再随机摸出一个小球,用列表的方法,求该同学两次摸出的小球所标字母相同的概率.
课堂练习
解:列表得
由列表可知可能出现的结果共9种,其中两次摸出的小球所标字母相同的情况数有3种.所以该同学两次摸出的小球所标字母相同的概率= = .
A B C
A (A,A) (B,A) (C,A)
B (A,B) (B,B) (C,B)
C (A,C) (B,C) (C,C)
课堂练习
列举法
关键
常用
方法
直接列举法
列表法
适用对象
两个试验因素或分两步进行的试验
基本步骤
列表;确定m、n值代入概率公式计算
在于正确列举出试验结果的各种可能性.
确保试验中每种结果出现的可能性大小相等
前提条件
课堂小结
谢 谢
同课章节目录
