《三角函数》专题14 诱导公式(基础)学案(Word版含答案)
文档属性
| 名称 | 《三角函数》专题14 诱导公式(基础)学案(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 419.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-26 15:41:13 | ||
图片预览


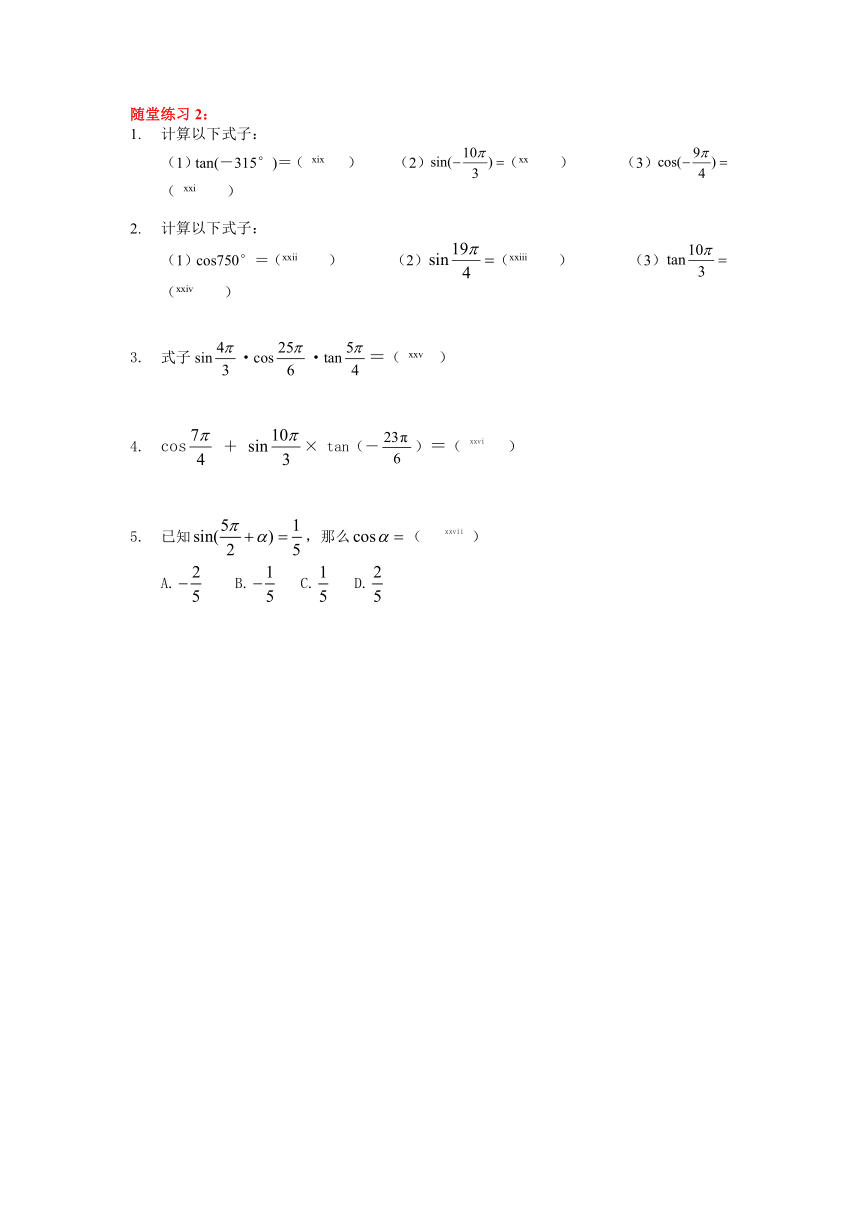


文档简介
《三角函数》专题14-1 诱导公式(基础)
(10套,8页,含答案)
知识点1:
诱导公式:记住六个公式: ,,; ,,; 其他套口诀:正负看象限,纵变横不变 (,) 要变: 等 不变: 等
典型例题1:
[endnoteRef:0]; [endnoteRef:1]; [endnoteRef:2]; [0: ] [1: ] [2: ]
[endnoteRef:3]; [endnoteRef:4]; [endnoteRef:5]; [3: ] [4: ] [5: ]
随堂练习1:
[endnoteRef:6]; [endnoteRef:7]; [endnoteRef:8]; [6: ] [7: ] [8: ]
[endnoteRef:9]; [endnoteRef:10]; [endnoteRef:11]; [9: ] [10: ] [11: ]
化简以下式子:([endnoteRef:12]) [12: 答案:
1. ; ; ;
2. ; ; ;
3.; ; ;
4.; ; ;
5.; ;
6.; ;
7.; ;
8.; ;
]
1. ; ; ;
2.sin ; cos ; tan ;
3.sin ; cos ; tan ;
4.sin ; cos ; tan ;
5.sin ; cos ;
6.sin ;cos ;
7.sin ;cos ;
8.sin ;cos ;
三角函数化简: 三角函数综合运算的题型,综合了特殊角值识记、基本公式、诱导公式等,对知识的融会贯通,运算能力的整体提升非常有帮助。希望大家将此作为重点,反复训练。 基本套路: 负角变正角: 有负号的先处理负号,运用以下三个公式:
,,;
大角变小角:
一般如果角度大于360度(),那么就把该角度减去360度,一直减至最小正角。或者把该角度除以360度,取余数;
,,;
角度大于90度,则利用诱导公式变成90度以内的正角。常用的角度转换如下:
120=180-60 例如:sin120 = sin(180-60) = sin60 ;
135=180-45 例如:cos135 = cos(180-45) = - cos45 ;
150=180-30 例如:tan150 = tan(180-30) = - tan30 ;
210=180+30 例如:cos210 = cos(180+30) = - cos30 ;
225=180+45 例如:tan225 = tan(180+45) =tan45 ;
240=180+60 例如:sin240 = sin(180+60) = - sin60 ;
300=360-60 例如:tain300 = tan(360-60) = - tan60 ;
315=360-45 例如:sin315 = sin(360-45) = - sin45 ;
330=360-30 例如:cos330 = cos(360-30) = cos30 ; 最后代入特殊角值即可;
典型例题2:
计算:(1)sin300°=( [endnoteRef:13] ) (2)tan225°=( [endnoteRef:14] ) (3)cos=( [endnoteRef:15] ) [13: 答案:;] [14: 答案:1;] [15: 答案:;]
计算:式子的值等于( [endnoteRef:16] ).
[16: 答案:;]
计算:式子的值是( [endnoteRef:17] ) [17: 答案:1;]
随堂练习2:
计算以下式子:
(1)tan(-315°)=( [endnoteRef:18] ) (2)([endnoteRef:19] ) (3) ( [endnoteRef:20] ) [18: 答案:1;] [19: 答案:;] [20: 答案:;]
计算以下式子:
(1)cos750°=([endnoteRef:21] ) (2)([endnoteRef:22] ) (3)([endnoteRef:23] ) [21: 答案:;] [22: 答案:;] [23: 答案:;]
式子sin·cos·tan=( [endnoteRef:24] ) [24: 答案:-;]
cos + × tan(-)=( [endnoteRef:25] ) [25: 答案:;]
已知,那么( [endnoteRef:26] )
A. B. C. D. [26: 答案:C;]
《三角函数》专题14-2 诱导公式(基础)
计算: [endnoteRef:27] ; sin [endnoteRef:28] ; tan [endnoteRef:29] ; [27: 答案:;] [28: 答案:;] [29: 答案:;]
sin[endnoteRef:30] ; cos[endnoteRef:31] ; cos[endnoteRef:32] ; [30: 答案:;] [31: 答案:;] [32: 答案:;]
cos[endnoteRef:33] ; sin[endnoteRef:34] ; sin[endnoteRef:35] ; [33: 答案:;] [34: 答案:;] [35: 答案:;]
计算:(1)sin225°=( [endnoteRef:36] ) (2)cos330°=( [endnoteRef:37] ) (3)tan=( [endnoteRef:38] ) [36: 答案:;] [37: 答案:;] [38: 答案:;]
(4)tan(-600°)×sin150° + cos225°=([endnoteRef:39]) (5)×cos× =([endnoteRef:40]) [39: 答案:;] [40: 答案:;]
(6)++sin= ( [endnoteRef:41] ) [41: 答案:;]
式子sin2(+)-cos(+)·cos(-)+1的值为( [endnoteRef:42]) A.1 B. C.0 D.2 [42: 答案:D;]
《三角函数》专题14-3 诱导公式(基础)
计算:sin[endnoteRef:43] ; tan[endnoteRef:44] ; cos [endnoteRef:45] ; [43: 答案:;] [44: 答案:;] [45: 答案:;]
cos[endnoteRef:46] ; sin[endnoteRef:47] ; cos [endnoteRef:48] ; [46: 答案:;] [47: 答案:;] [48: 答案:;]
sin[endnoteRef:49] ; cos[endnoteRef:50] ; tan [endnoteRef:51] ; [49: 答案:;] [50: 答案:;] [51: 答案:;]
计算:(1)tan=( [endnoteRef:52] ) (2)sin=( [endnoteRef:53] ) (3)cos210°=( [endnoteRef:54] ) [52: 答案:1;] [53: 答案:;] [54: 答案:;]
(4)tan 690° sin240°÷cos150°=([endnoteRef:55] ) (5)cos÷+=([endnoteRef:56] ) [55: 答案:-;] [56: 答案:1;]
(6)tan240°× cos(-1125°)-sin(-765°)=( [endnoteRef:57] ) [57: 答案:;]
化简所得的结果是( [endnoteRef:58] )
A.2sin2 B.-2sin2 C.0 D.-1 [58: 答案:B;]
《三角函数》专题14-4 诱导公式(基础)
计算:tan[endnoteRef:59] ; cos[endnoteRef:60] ; cos[endnoteRef:61] ; [59: 答案:;] [60: 答案:;] [61: 答案:;]
sin[endnoteRef:62] ; sin[endnoteRef:63] ; cos[endnoteRef:64] ; [62: 答案:;] [63: 答案:;] [64: 答案:;;]
cos[endnoteRef:65] ; cos[endnoteRef:66] ; sin [endnoteRef:67] ; [65: 答案:;] [66: 答案:;] [67: 答案:;]
计算:(1)cos120°=( [endnoteRef:68] ) (2)sin210°=( [endnoteRef:69] ) (3)tan=( [endnoteRef:70] ) [68: 答案:;] [69: 答案:;] [70: 答案:;]
(4)式子的值等于( [endnoteRef:71] )
[71: 答案:;]
(5)=( [endnoteRef:72] ) (6)tan-sin()×cos=([endnoteRef:73] ) [72: 答案:0;] [73: 答案:;]
已知sin(-)-cos(+)=.求sin-cos;([endnoteRef:74]) [74: 答案:;]
《三角函数》专题14-5 诱导公式(基础)
计算:cos [endnoteRef:75] ; tan[endnoteRef:76] ; sin[endnoteRef:77] ; [75: 答案:;] [76: 答案:;] [77: 答案:;]
sin[endnoteRef:78] ; sin[endnoteRef:79] ; cos[endnoteRef:80] ; [78: 答案:;] [79: 答案:;] [80: 答案:;]
tan[endnoteRef:81] ; sin [endnoteRef:82] ; sin[endnoteRef:83] ; [81: 答案:;] [82: 答案:;] [83: 答案:;]
计算:(1)tan315°=( [endnoteRef:84] ) (2)sin=( [endnoteRef:85] ) (3)cos=( [endnoteRef:86] ) [84: 答案:;] [85: 答案:;] [86: 答案:;]
计算:(1)式子([endnoteRef:87]) [87: 答案:0;]
(2)=([endnoteRef:88]) (3)sin--=([endnoteRef:89]) [88: 答案:2;] [89: 答案:;]
若 ,则 的值为( [endnoteRef:90] ). [90: 答案:;]
《三角函数》专题14-6 诱导公式(基础)
计算:tan[endnoteRef:91] ; cos[endnoteRef:92] ; sin[endnoteRef:93] ; [91: 答案:;] [92: 答案:;] [93: 答案:;]
tan[endnoteRef:94] ; sin [endnoteRef:95] ; cos [endnoteRef:96] ; [94: 答案:;] [95: 答案:;] [96: 答案:;]
cos[endnoteRef:97] ; cos [endnoteRef:98] ; sin[endnoteRef:99] ; [97: 答案:;] [98: 答案:;] [99: 答案:;]
计算:(1)cos300°=( [endnoteRef:100] ) (2)tan=( [endnoteRef:101] ) (3)sin120°=( [endnoteRef:102] ) [100: 答案:;] [101: 答案:;] [102: 答案:;]
计算:(1)sin(-1200°)cos1290°+ cos(-1020°)sin(-1050°) + tan945°=([endnoteRef:103] ) [103: 答案:2;]
(2) [endnoteRef:104] [104: 答案:0;]
(3)sin÷cos×=( [endnoteRef:105] ) [105: 答案:;]
《三角函数》专题14-7 诱导公式(基础)
计算:sin [endnoteRef:106] ; cos[endnoteRef:107] ; sin[endnoteRef:108] ; [106: 答案:;] [107: 答案:;] [108: 答案:;]
[endnoteRef:109] ; sin [endnoteRef:110] ; tan[endnoteRef:111] ; [109: 答案:;] [110: 答案:;] [111: 答案:;]
cos[endnoteRef:112] ; cos [endnoteRef:113] ; cos[endnoteRef:114] ; [112: 答案:;] [113: 答案:;] [114: 答案:;]
计算:(1)sin=( [endnoteRef:115] ) (2)tan=([endnoteRef:116] ) (3)cos240°=([endnoteRef:117] ) [115: 答案:;] [116: 答案:;] [117: 答案:;]
计算:(1)([endnoteRef:118]) [118: 答案:0;]
(2)=([endnoteRef:119] ) (3)×÷sin=([endnoteRef:120] ) [119: 答案:0;] [120: 答案:;]
下列各式不正确的是( [endnoteRef:121] )
A. sin(α+180°)=-sinα B.cos(-α+β)=-cos(α-β)
C. sin(-α-360°)=-sinα D.cos(-α-β)=cos(α+β) [121: 答案:B;]
《三角函数》专题14-8 诱导公式(基础)
计算:sin[endnoteRef:122] ; [endnoteRef:123] ; cos[endnoteRef:124] ; [122: 答案:;] [123: 答案:;] [124: 答案:;]
cos[endnoteRef:125] ; cos [endnoteRef:126] ; cos[endnoteRef:127] ; [125: 答案:;] [126: 答案:;] [127: 答案:;]
sin[endnoteRef:128] ; tan[endnoteRef:129] ; sin[endnoteRef:130] ; [128: 答案:;] [129: 答案:;] [130: 答案:; ]
计算:(1)tan330°=([endnoteRef:131] ) (2)cos135°=( [endnoteRef:132] ) (3)sin=( [endnoteRef:133] ) [131: 答案:; ] [132: 答案:; ] [133: 答案:; ]
(4)tan135°-cos 750°÷sin330°=( [endnoteRef:134]) (5)cos÷ tan- sin=([endnoteRef:135] ) [134: 答案: ;] [135: 答案: ;]
(6)tan210°×sin(-765°)+cos2040°=( [endnoteRef:136] ) [136: 答案: ;]
《三角函数》专题14-9 诱导公式(基础)
计算:sin [endnoteRef:137] ; tan [endnoteRef:138] ; sin [endnoteRef:139] ;
cos[endnoteRef:140] ; sin[endnoteRef:141] ; cos[endnoteRef:142] ; [137: 答案:; ] [138: 答案:; ] [139: 答案:;] [140: 答案:;] [141: 答案:;] [142: 答案:;]
cos[endnoteRef:143] ; sin[endnoteRef:144] ; sin[endnoteRef:145] ; [143: 答案:;] [144: 答案:;] [145: 答案:;]
计算:(1)cos=([endnoteRef:146] ) (2)tan=( [endnoteRef:147] ) (3)sin135°=( [endnoteRef:148] ) [146: 答案:;] [147: 答案:;] [148: 答案:;]
(4)tan2010°+×cos315°=([endnoteRef:149]) (5)cos×÷=([endnoteRef:150] ) [149: 答案:;] [150: 答案:;]
(6)÷×sin=( [endnoteRef:151] ) [151: 答案:;]
已知,则下列不等式关系必定成立的是( [endnoteRef:152] )
A. B.
C. D. [152: 答案:B;]
《三角函数》专题14-10 诱导公式 (基础)
化简以下式子:([endnoteRef:153]) [153: 答案:
1. ; ; ;
2. ; ; ;
3.; ; ;
4.; ; ;
5.; ;
6.; ;
7.; ;
8.; ;
]
1. ; ; ;
2.sin ; cos ; tan ;
3.sin ; cos ; tan ;
4.sin ; cos ; tan ;
5.sin ; cos ;
6.sin ;cos ;
7.sin ;cos ;
8.sin ;cos ;
计算:
(1)tan=( [endnoteRef:154] ) (2)cos=( [endnoteRef:155] ) (3)sin315°=( [endnoteRef:156] ) [154: 答案:;] [155: 答案:;] [156: 答案:;]
计算:
求cos(-2640°)+sin1665°+ tan300°+tan765°的值.([endnoteRef:157])
[157: 答案:;]
cos×+([endnoteRef:158] ) [158: 答案:;]
已知,则 [endnoteRef:159] . [159: 答案:;]
(10套,8页,含答案)
知识点1:
诱导公式:记住六个公式: ,,; ,,; 其他套口诀:正负看象限,纵变横不变 (,) 要变: 等 不变: 等
典型例题1:
[endnoteRef:0]; [endnoteRef:1]; [endnoteRef:2]; [0: ] [1: ] [2: ]
[endnoteRef:3]; [endnoteRef:4]; [endnoteRef:5]; [3: ] [4: ] [5: ]
随堂练习1:
[endnoteRef:6]; [endnoteRef:7]; [endnoteRef:8]; [6: ] [7: ] [8: ]
[endnoteRef:9]; [endnoteRef:10]; [endnoteRef:11]; [9: ] [10: ] [11: ]
化简以下式子:([endnoteRef:12]) [12: 答案:
1. ; ; ;
2. ; ; ;
3.; ; ;
4.; ; ;
5.; ;
6.; ;
7.; ;
8.; ;
]
1. ; ; ;
2.sin ; cos ; tan ;
3.sin ; cos ; tan ;
4.sin ; cos ; tan ;
5.sin ; cos ;
6.sin ;cos ;
7.sin ;cos ;
8.sin ;cos ;
三角函数化简: 三角函数综合运算的题型,综合了特殊角值识记、基本公式、诱导公式等,对知识的融会贯通,运算能力的整体提升非常有帮助。希望大家将此作为重点,反复训练。 基本套路: 负角变正角: 有负号的先处理负号,运用以下三个公式:
,,;
大角变小角:
一般如果角度大于360度(),那么就把该角度减去360度,一直减至最小正角。或者把该角度除以360度,取余数;
,,;
角度大于90度,则利用诱导公式变成90度以内的正角。常用的角度转换如下:
120=180-60 例如:sin120 = sin(180-60) = sin60 ;
135=180-45 例如:cos135 = cos(180-45) = - cos45 ;
150=180-30 例如:tan150 = tan(180-30) = - tan30 ;
210=180+30 例如:cos210 = cos(180+30) = - cos30 ;
225=180+45 例如:tan225 = tan(180+45) =tan45 ;
240=180+60 例如:sin240 = sin(180+60) = - sin60 ;
300=360-60 例如:tain300 = tan(360-60) = - tan60 ;
315=360-45 例如:sin315 = sin(360-45) = - sin45 ;
330=360-30 例如:cos330 = cos(360-30) = cos30 ; 最后代入特殊角值即可;
典型例题2:
计算:(1)sin300°=( [endnoteRef:13] ) (2)tan225°=( [endnoteRef:14] ) (3)cos=( [endnoteRef:15] ) [13: 答案:;] [14: 答案:1;] [15: 答案:;]
计算:式子的值等于( [endnoteRef:16] ).
[16: 答案:;]
计算:式子的值是( [endnoteRef:17] ) [17: 答案:1;]
随堂练习2:
计算以下式子:
(1)tan(-315°)=( [endnoteRef:18] ) (2)([endnoteRef:19] ) (3) ( [endnoteRef:20] ) [18: 答案:1;] [19: 答案:;] [20: 答案:;]
计算以下式子:
(1)cos750°=([endnoteRef:21] ) (2)([endnoteRef:22] ) (3)([endnoteRef:23] ) [21: 答案:;] [22: 答案:;] [23: 答案:;]
式子sin·cos·tan=( [endnoteRef:24] ) [24: 答案:-;]
cos + × tan(-)=( [endnoteRef:25] ) [25: 答案:;]
已知,那么( [endnoteRef:26] )
A. B. C. D. [26: 答案:C;]
《三角函数》专题14-2 诱导公式(基础)
计算: [endnoteRef:27] ; sin [endnoteRef:28] ; tan [endnoteRef:29] ; [27: 答案:;] [28: 答案:;] [29: 答案:;]
sin[endnoteRef:30] ; cos[endnoteRef:31] ; cos[endnoteRef:32] ; [30: 答案:;] [31: 答案:;] [32: 答案:;]
cos[endnoteRef:33] ; sin[endnoteRef:34] ; sin[endnoteRef:35] ; [33: 答案:;] [34: 答案:;] [35: 答案:;]
计算:(1)sin225°=( [endnoteRef:36] ) (2)cos330°=( [endnoteRef:37] ) (3)tan=( [endnoteRef:38] ) [36: 答案:;] [37: 答案:;] [38: 答案:;]
(4)tan(-600°)×sin150° + cos225°=([endnoteRef:39]) (5)×cos× =([endnoteRef:40]) [39: 答案:;] [40: 答案:;]
(6)++sin= ( [endnoteRef:41] ) [41: 答案:;]
式子sin2(+)-cos(+)·cos(-)+1的值为( [endnoteRef:42]) A.1 B. C.0 D.2 [42: 答案:D;]
《三角函数》专题14-3 诱导公式(基础)
计算:sin[endnoteRef:43] ; tan[endnoteRef:44] ; cos [endnoteRef:45] ; [43: 答案:;] [44: 答案:;] [45: 答案:;]
cos[endnoteRef:46] ; sin[endnoteRef:47] ; cos [endnoteRef:48] ; [46: 答案:;] [47: 答案:;] [48: 答案:;]
sin[endnoteRef:49] ; cos[endnoteRef:50] ; tan [endnoteRef:51] ; [49: 答案:;] [50: 答案:;] [51: 答案:;]
计算:(1)tan=( [endnoteRef:52] ) (2)sin=( [endnoteRef:53] ) (3)cos210°=( [endnoteRef:54] ) [52: 答案:1;] [53: 答案:;] [54: 答案:;]
(4)tan 690° sin240°÷cos150°=([endnoteRef:55] ) (5)cos÷+=([endnoteRef:56] ) [55: 答案:-;] [56: 答案:1;]
(6)tan240°× cos(-1125°)-sin(-765°)=( [endnoteRef:57] ) [57: 答案:;]
化简所得的结果是( [endnoteRef:58] )
A.2sin2 B.-2sin2 C.0 D.-1 [58: 答案:B;]
《三角函数》专题14-4 诱导公式(基础)
计算:tan[endnoteRef:59] ; cos[endnoteRef:60] ; cos[endnoteRef:61] ; [59: 答案:;] [60: 答案:;] [61: 答案:;]
sin[endnoteRef:62] ; sin[endnoteRef:63] ; cos[endnoteRef:64] ; [62: 答案:;] [63: 答案:;] [64: 答案:;;]
cos[endnoteRef:65] ; cos[endnoteRef:66] ; sin [endnoteRef:67] ; [65: 答案:;] [66: 答案:;] [67: 答案:;]
计算:(1)cos120°=( [endnoteRef:68] ) (2)sin210°=( [endnoteRef:69] ) (3)tan=( [endnoteRef:70] ) [68: 答案:;] [69: 答案:;] [70: 答案:;]
(4)式子的值等于( [endnoteRef:71] )
[71: 答案:;]
(5)=( [endnoteRef:72] ) (6)tan-sin()×cos=([endnoteRef:73] ) [72: 答案:0;] [73: 答案:;]
已知sin(-)-cos(+)=.求sin-cos;([endnoteRef:74]) [74: 答案:;]
《三角函数》专题14-5 诱导公式(基础)
计算:cos [endnoteRef:75] ; tan[endnoteRef:76] ; sin[endnoteRef:77] ; [75: 答案:;] [76: 答案:;] [77: 答案:;]
sin[endnoteRef:78] ; sin[endnoteRef:79] ; cos[endnoteRef:80] ; [78: 答案:;] [79: 答案:;] [80: 答案:;]
tan[endnoteRef:81] ; sin [endnoteRef:82] ; sin[endnoteRef:83] ; [81: 答案:;] [82: 答案:;] [83: 答案:;]
计算:(1)tan315°=( [endnoteRef:84] ) (2)sin=( [endnoteRef:85] ) (3)cos=( [endnoteRef:86] ) [84: 答案:;] [85: 答案:;] [86: 答案:;]
计算:(1)式子([endnoteRef:87]) [87: 答案:0;]
(2)=([endnoteRef:88]) (3)sin--=([endnoteRef:89]) [88: 答案:2;] [89: 答案:;]
若 ,则 的值为( [endnoteRef:90] ). [90: 答案:;]
《三角函数》专题14-6 诱导公式(基础)
计算:tan[endnoteRef:91] ; cos[endnoteRef:92] ; sin[endnoteRef:93] ; [91: 答案:;] [92: 答案:;] [93: 答案:;]
tan[endnoteRef:94] ; sin [endnoteRef:95] ; cos [endnoteRef:96] ; [94: 答案:;] [95: 答案:;] [96: 答案:;]
cos[endnoteRef:97] ; cos [endnoteRef:98] ; sin[endnoteRef:99] ; [97: 答案:;] [98: 答案:;] [99: 答案:;]
计算:(1)cos300°=( [endnoteRef:100] ) (2)tan=( [endnoteRef:101] ) (3)sin120°=( [endnoteRef:102] ) [100: 答案:;] [101: 答案:;] [102: 答案:;]
计算:(1)sin(-1200°)cos1290°+ cos(-1020°)sin(-1050°) + tan945°=([endnoteRef:103] ) [103: 答案:2;]
(2) [endnoteRef:104] [104: 答案:0;]
(3)sin÷cos×=( [endnoteRef:105] ) [105: 答案:;]
《三角函数》专题14-7 诱导公式(基础)
计算:sin [endnoteRef:106] ; cos[endnoteRef:107] ; sin[endnoteRef:108] ; [106: 答案:;] [107: 答案:;] [108: 答案:;]
[endnoteRef:109] ; sin [endnoteRef:110] ; tan[endnoteRef:111] ; [109: 答案:;] [110: 答案:;] [111: 答案:;]
cos[endnoteRef:112] ; cos [endnoteRef:113] ; cos[endnoteRef:114] ; [112: 答案:;] [113: 答案:;] [114: 答案:;]
计算:(1)sin=( [endnoteRef:115] ) (2)tan=([endnoteRef:116] ) (3)cos240°=([endnoteRef:117] ) [115: 答案:;] [116: 答案:;] [117: 答案:;]
计算:(1)([endnoteRef:118]) [118: 答案:0;]
(2)=([endnoteRef:119] ) (3)×÷sin=([endnoteRef:120] ) [119: 答案:0;] [120: 答案:;]
下列各式不正确的是( [endnoteRef:121] )
A. sin(α+180°)=-sinα B.cos(-α+β)=-cos(α-β)
C. sin(-α-360°)=-sinα D.cos(-α-β)=cos(α+β) [121: 答案:B;]
《三角函数》专题14-8 诱导公式(基础)
计算:sin[endnoteRef:122] ; [endnoteRef:123] ; cos[endnoteRef:124] ; [122: 答案:;] [123: 答案:;] [124: 答案:;]
cos[endnoteRef:125] ; cos [endnoteRef:126] ; cos[endnoteRef:127] ; [125: 答案:;] [126: 答案:;] [127: 答案:;]
sin[endnoteRef:128] ; tan[endnoteRef:129] ; sin[endnoteRef:130] ; [128: 答案:;] [129: 答案:;] [130: 答案:; ]
计算:(1)tan330°=([endnoteRef:131] ) (2)cos135°=( [endnoteRef:132] ) (3)sin=( [endnoteRef:133] ) [131: 答案:; ] [132: 答案:; ] [133: 答案:; ]
(4)tan135°-cos 750°÷sin330°=( [endnoteRef:134]) (5)cos÷ tan- sin=([endnoteRef:135] ) [134: 答案: ;] [135: 答案: ;]
(6)tan210°×sin(-765°)+cos2040°=( [endnoteRef:136] ) [136: 答案: ;]
《三角函数》专题14-9 诱导公式(基础)
计算:sin [endnoteRef:137] ; tan [endnoteRef:138] ; sin [endnoteRef:139] ;
cos[endnoteRef:140] ; sin[endnoteRef:141] ; cos[endnoteRef:142] ; [137: 答案:; ] [138: 答案:; ] [139: 答案:;] [140: 答案:;] [141: 答案:;] [142: 答案:;]
cos[endnoteRef:143] ; sin[endnoteRef:144] ; sin[endnoteRef:145] ; [143: 答案:;] [144: 答案:;] [145: 答案:;]
计算:(1)cos=([endnoteRef:146] ) (2)tan=( [endnoteRef:147] ) (3)sin135°=( [endnoteRef:148] ) [146: 答案:;] [147: 答案:;] [148: 答案:;]
(4)tan2010°+×cos315°=([endnoteRef:149]) (5)cos×÷=([endnoteRef:150] ) [149: 答案:;] [150: 答案:;]
(6)÷×sin=( [endnoteRef:151] ) [151: 答案:;]
已知,则下列不等式关系必定成立的是( [endnoteRef:152] )
A. B.
C. D. [152: 答案:B;]
《三角函数》专题14-10 诱导公式 (基础)
化简以下式子:([endnoteRef:153]) [153: 答案:
1. ; ; ;
2. ; ; ;
3.; ; ;
4.; ; ;
5.; ;
6.; ;
7.; ;
8.; ;
]
1. ; ; ;
2.sin ; cos ; tan ;
3.sin ; cos ; tan ;
4.sin ; cos ; tan ;
5.sin ; cos ;
6.sin ;cos ;
7.sin ;cos ;
8.sin ;cos ;
计算:
(1)tan=( [endnoteRef:154] ) (2)cos=( [endnoteRef:155] ) (3)sin315°=( [endnoteRef:156] ) [154: 答案:;] [155: 答案:;] [156: 答案:;]
计算:
求cos(-2640°)+sin1665°+ tan300°+tan765°的值.([endnoteRef:157])
[157: 答案:;]
cos×+([endnoteRef:158] ) [158: 答案:;]
已知,则 [endnoteRef:159] . [159: 答案:;]
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
