1.4.2用空间向量研究距离、夹角问题: 二面角(中档)同步练习(Word版含解析)
文档属性
| 名称 | 1.4.2用空间向量研究距离、夹角问题: 二面角(中档)同步练习(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-26 15:52:10 | ||
图片预览




文档简介
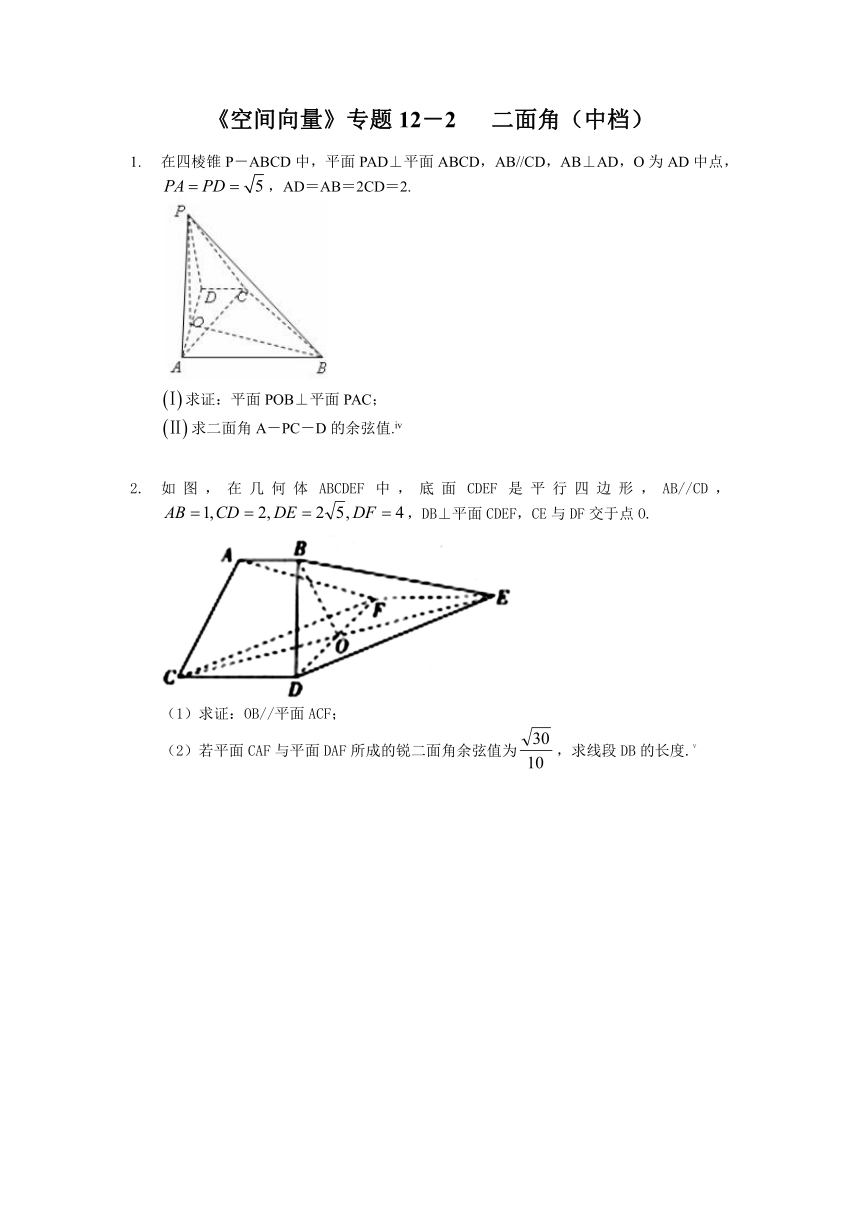
《空间向量》专题12-1 二面角(中档)
(8套,8页,含答案)
如图,在三棱台ABC-DEF中,二面角B-AD-C是直二面角,AB⊥AC,AB=3,.
(1)求证:AB⊥平面ACFD;
(2)求二面角F-BE-D的平面角的余弦值[endnoteRef:0].
[0: 答案:;
(1)连接,在等腰梯形中,过作交于点,因为,所以,,,所以,所以,即, 2分
又二面角是直二面角,平面,所以平面, 4分
又平面,所以,又因为,,、平面,所以平面. 6分
(2)如图,在平面内,过点作,由(1)可知,以为原点,,,的方向为轴,轴,轴的正方向,建立空间直角坐标系.
则,,,, 7分
所以,,设是平面的一个法向量,则,所以,
取,则,,
即, 9分
由(1)可知平面,
所以是平面的一个法向量, 10分
所以, 11分
又二面角的平面角为锐角,
所以二面角的平面角的余弦值为. 12分]
如图,在梯形ABCD中,AB//CD,AD=DC=CB=2,∠ABC=60°,平面ACEF⊥平面ABCD,四边形ACEF是菱形,∠CAF=60°.
(1)求证:BF⊥AE;
(2)求二面角B-EF-D的平面角的正切值.([endnoteRef:1])
[1: 答案:;
【解析】(1)依题意,在等腰梯形中,,,
∵,∴,即,·········1分
∵平面平面,∴平面,·········2分
而平面,∴.·········3分
连接,∵四边形是菱形,∴,·········4分
∴平面,
∵平面,∴.·········6分
(2)取的中点,连接,因为四边形是菱形,且.
所以由平面几何易知,∵平面平面,∴平面.
故此可以、、分别为、、轴建立空间直角坐标系,各点的坐标依次为:,,,,,.······7分
设平面和平面的法向量分别为,,
∵,.
∴由,令,则,··9分
同理,求得.·········10分
∴,故二面角的平面角的正切值为.·······12分
]
已知四棱锥S-ABCD,SA⊥平面ABCD,底面ABCD为直角梯形,AB//DC,∠DAB=90°,
AB=2DC,,M是SB中点.
(1)求证:CM//平面SAD;
(2)若直线DM与平面SAB所成角的正切值为,F是SC的中点,求二面角C-AF-D的余弦值.([endnoteRef:2])
[2: 答案:;
【解析】(1)证明:取中点,连接,,
在中,,,,,
四边形为平行四边形.·········2分
,·········3分
又平面,平面,
平面.·········4分
(2)由已知得:,,两两垂直,以,,所在直线分别为轴,轴,轴建立如图所示的空间直角坐标系.·········5分
,,,平面,
就是与平面所成的角.
在中,,即,·········7分
设,则,,;
中,为斜边中点,,
.
则,,,,,
所以,,.
设是平面的一个法向量,则
,
令,得.·········9分
设是平面的一个法向量,则
,
令,.·········11分
.
二面角的余弦值为.·········12分]
《空间向量》专题12-2 二面角(中档)
在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB//CD,AB⊥AD,O为AD中点,,AD=AB=2CD=2.
求证:平面POB⊥平面PAC;
求二面角A-PC-D的余弦值.[endnoteRef:3]
[3: 答案:;
证明:由条件可知,,,
,.
,且为中点,.
,平面.
又平面,.
又,平面.
平面,平面平面.
解:以为空间坐标原点,建立如图所示的空间直角坐标系,则,,,,,,,,
设为平面的一个法向量,
由得,解得.
令,则.
同理可得,平面的一个法向量,
二面角的平面角的余弦值.
]
如图,在几何体ABCDEF中,底面CDEF是平行四边形,AB//CD,,DB⊥平面CDEF,CE与DF交于点O.
(1)求证:OB//平面ACF;
(2)若平面CAF与平面DAF所成的锐二面角余弦值为,求线段DB的长度.[endnoteRef:4]
[4: 答案:或;
解:(Ⅰ)取中点,连接,
在中,是的中点,是的中点,
所以,
又,
所以
所以四边形为平行四边形,
所以,
又因为平面,平面,
故平面.
(Ⅱ)由,,
可得,所以,
又平面,故以为坐标原点,直线分别为轴建立如图所示的空间直角坐标系,则,,,设,则,,
所以,,.
设平面的一个法向量,
则即,
取得,
设平面的一个法向量,
则即,
取得,
设平面与平面所成的锐二面角为,
则,
整理得,
解得或,
所以或.
]
《空间向量》专题12-3 二面角(中档)
如图,四棱锥P-ABCD中,PA⊥底面ABCD,ABCD为直角梯形,AD//BC,AD⊥AB,,AC∩BD=O,过O点作平面α平行于平面PAB,平面α与棱BC,AD,PD,PC分别相交于点E,F,G,H.
(1)求GH的长度;
(2)求二面角B-FH-E的余弦值.[endnoteRef:5]
[5: 答案:,;
解:(Ⅰ)【法一】(Ⅰ)因为平面,平面平面,
,平面平面,所以,同理,
因为∥,所以∽,且,
所以,,
同理,连接,则有∥,
所以,,所以,同理,,
过点作∥交于,则
【法二】因为平面,平面平面,,
平面平面,
根据面面平行的性质定理,所以,同理,
因为,所以,且,
又因为∽,,所以,
同理,,
如图:作,
所以,故四边形为矩形,即,
在中,所以,所以.
(Ⅱ)建立如图所示空间直角坐标系,
, 设平面的法向量为,
,令,得,
因为平面平面,所以平面的法向量
,二面角的余弦值为.
]
如图,在四棱柱ABCD-A1B1C1D1中,AB//CD,AB=BC=CC1=2CD,E为线段AB的中点,F是线段DD1上的动点.
(Ⅰ)求证:EF∥平面BCC1B1
(Ⅱ)若∠BCD=∠C1CD=60°,且平面D1C1CD⊥平面ABCD,求平面BCC1B1与DC1B1平面所成角(锐角)的余弦值.[endnoteRef:6]
[6: 答案:;
证明:(1)连结DE,D1E,∵AB∥CD,AB=2CD,E是AB的中点,
∴BE∥CD,BE=CD, ∴四边形BCDE是平行四边形,
∴DE∥BC,又DE平面BCC1B1,
∴DE∥平面BCC1B1, 同理D1D∥平面BCC1B1,又D1D∩DE=D,
∴平面DED1∥平面BCC1B1, ∵EF平面DED1,
∴EF∥平面BCC1B1. ................6分
方法一(2)∵AB=BC=CC1=2CD,∠BCD=∠C1CD=60°,
设CD=1,则BC=2,BD2=3 ∴BD⊥CD. 同理:C1D⊥CD,
∵平面D1C1CD⊥平面ABCD,平面D1C1CD∩平面ABCD=CD,C1D平面D1C1CD,
∴C1D⊥平面ABCD, ∴C1D⊥BC.∴C1D⊥B1C1
在平面ABCD中,过D作DH⊥BC,垂足为H,连结C1H.
∴BC⊥平面C1DH,∵C1H平面C1DH,
∴BC⊥C1H, 所以,B1C1⊥C1H,
∴∠DC1H为平面BCC1B1与DC1B1平面所成的角.
在Rt△BCD中, C1D=, 在Rt△C1DH,C1H=,∴cos∠DC1H=
∴平面BCC1B1与DC1B1平面所成的角(锐角)的余弦值为 ................12分
方法二:可以建立空间坐标系解答,(略)]
如图,在三棱柱ABC-A1B1C1中,∠AA1B1=45°,AC=BC,平面BB1C1C⊥平面AA1B1B,E为CC1中点.
(1)求证:BB1⊥AC;
(2)若直线A1C1与平面ABB1A1所成角为45°,求平面A1B1E与平面ABC所成锐二面角的余弦值.[endnoteRef:7]
[7: 答案:;
【证明】(1)过点做交于,因为面 ,,
所以,故,………2分
又因为,所以,故,
因为,所以,又因为,所以面,
故.………5分
(2)以为坐标原点,所在直线为轴,建立空间直角坐标,
,
设面的法向量为, 则令,
得; ………7分
设面的法向量为,则令
得;………9分
………11分
面与面所成锐二面角的余弦值为.………12分
]
《空间向量》专题12-4 二面角(中档)
如图所示,该几何体是由一个直三棱柱ADE-BCF和一个四棱锥P-ABCD组合而成,其中.
(1)证明:AD⊥平面ABFE;
(2)若四棱锥P-ABCD的高2,求二面角C-AF-P的余弦值.[endnoteRef:8]
[8: 答案:;
(1)证明:直三棱柱中,平面,所以,
又,所以平面;
(2)解:由(1)知平面,以为原点,方向为轴建立空间直角坐标系(如图所示),,则,,,,,,,设平面的一个法向量,
则,取,则,所以.
设平面的一个法向量,则,取,则.
所以,所以,
因为二面角的平面角是锐角,所以所求二面角的余弦值为.
]
如图,三棱台ABC﹣A1B1C1中,侧面A1B1BA与侧面A1C1CA是全等的梯形,
若A1A⊥AB,A1A⊥A1C1,且AB=2A1B1=4A1A.
(Ⅰ)若,,证明:DE∥平面BCC1B1;
(Ⅱ)若二面角C1﹣AA1﹣B为,求平面A1B1BA与平面C1B1BC所成的锐二面角的余弦值.[endnoteRef:9]
[9: 答案:;
【解答】(Ⅰ)证明:连接AC1,BC1,
在梯形A1C1CA中,AC=2A1C1,
∵AC1∩A1C=D,,
∴,
又,∴DE∥BC1,
∵BC1 平面BCC1B1,DE 平面BCC1B1,
∴DE∥平面BCC1B1 ;
(Ⅱ)解:侧面A1C1CA是梯形,∵A1A⊥A1C1,∴AA1⊥AC,
又A1A⊥AB,∴∠BAC为二面角C1﹣AA1﹣B的平面角,则∠BAC=,
∴△ABC,△A1B1C1均为正三角形,
在平面ABC内,过点A作AC的垂线,如图建立空间直角坐标系,
不妨设AA1=1,则A1B1=A1C1=2,AC=AC=4,
故点A1(0,0,1),C(0,4,0),.
设平面A1B1BA的法向量为,
则有,取,得;
设平面C1B1BC的法向量为,
则有,取,得.
∴,
故平面A1B1BA与平面C1B1BC所成的锐二面角的余弦值为.
]
《空间向量》专题12-5 二面角(中档)
如图,正三棱柱ABC-A1B1C1的所有棱长均2,D为棱BB1(不包括端点)上一动点,E是AB的中点.
(Ⅰ)若AD⊥A1C,求BD的长;
(Ⅱ)当D在棱BB1(不含端点)上运动时,求平面ADC1与平面ABC的夹角的余弦值的取值范围.[endnoteRef:10] [10: 答案:(,];
证明:(Ⅰ),由AC=BC,AE=BE,知CE⊥AB,
又平面ABC⊥平面ABB1A1,所以CE⊥平面ABB1A1
而AD 平面ABB1A1,∴AD⊥CE,又AD⊥A1C所以AD⊥平面A1CE,
所以AD⊥A1E.易知此时D为BB1的中点,故BD=1.…………………5分
(Ⅱ)以E为原点,EB为x轴,EC为y轴,
过E作垂直于平面ABC的垂线为z轴,
建立空间直角坐标系,设 BD=t,
则A(-1,0,0),D(1,0,t),C1(0,,2),
=(2,0,t),=(1,,2),设平面ADC1的法向量=(x,y,z),
则,取x=1,得,
平面ABC的法向量=(0,0,1),设平面ADC1与平面ABC的夹角为θ,
∴cosθ====
由于t∈(0,2),故cosθ∈(,].
即平面ADC1与平面ABC的夹角的余弦值的取值范围为(,].………………12分]
菱形ABCD的对角线AC与BD交于点O,AB=2,AC=6,点E,F分别在AD,CD上,,EF交BD于点H,将△DEF沿EF折到△D′EF位置,.
(1)证明:D′H⊥平面ABCD;
(2)求二面角B-D′A-C的正弦值.[endnoteRef:11]
[11: 答案:;
解:(1)∵,
∴,∴,
∵四边形为菱形,
∴,
∴,∴,∴
∵,
∴;
又,,∴,∴,∴,
∴,∴,又∵,
∴平面.
(Ⅱ)建立如图所示的空间直角坐标系:
,
,
设平面的一个法向量为,
由得,取,
∴,同理可得平面的法向量为,
∴,∴.
]
如图,在三棱锥P-ABC中,平面PAB⊥平面ABC,AB=6,,,D,E分别为线段AB,BC上的点,且AD=2DB,CE=2EB,PD⊥AC.
(1)求证:PD⊥平面ABC;
(2)若PA与平面ABC所成的角为,求平面PAC与平面PDE所成的锐二面角.[endnoteRef:12]
[12: 答案:;
(1)证明:连接,由题意知
,则,...............2分
又因为,所以
因为,都在平面内,
所以平面 ;...............4分
(2)由(1)知两两互相垂直,建立如图所示的直角坐标系,
且与平面所成的角为,有,
则
∴
因为
由(1)知平面,∴ 平面...............8分
∴为平面的一个法向量.
设平面的法向量为,则
∴,令,则,...............10分
∴为平面的一个法向量.
∴
故平面与平面的锐二面角的余弦值为,
所以平面与平面的锐二面角为................12分]
《空间向量》专题12-6 二面角(中档)
如图,四棱锥的底面是平行四边形,,.
(1)求异面直线与所成的角;
(2)若,,,求二面角的余弦值.[endnoteRef:13]
[13: 答案:90°,;
解:(1)取中点,连接,可证面,
所以异面直线与所成的角为90°
(2)设,则,,又,可得.
由(1)知,从而平面,
以为坐标原点,的方向分别为轴建立坐标系.
则,,,,
,所以,
,,,
可求得平面的法向量,
平面的法向量,
所以
又二面角为锐角,故二面角的余弦值为.
]
如图,在四棱锥中,平面,底面是菱形,,为与的交点,为上任意一点.
(1)证明:平面平面;
(2)若平面,并且二面角的大小为,求的值.[endnoteRef:14]
[14: 答案:;
解:(1)因为平面,∴,
又是菱形,∴,故平面
∴平面平面.
(2)解:连结,因为平面,
所以,所以平面,
又是的中点,故此时为的中点,
以为坐标原点,射线分别为轴建立空间直角坐标系
设,则,
向量为平面的一个法向量
设平面的一个法向量为,
则且
即且,
取,则,,则
∴,解得
故.
]
《空间向量》专题12-7 二面角(中档)
如图,四边形是圆柱的轴截面,点在圆柱的底面圆周上,是的中点,圆柱的底面圆的半径,侧面积为,.
(Ⅰ)求证:;
(Ⅱ)求二面角的平面角的余弦值.([endnoteRef:15])
[15: 答案:;
解:(Ⅰ)(解法一):由题意可知 ,解得 ,……分
在中,, …………分
∴,又∵是的中点,∴. ① …………分
∵为圆的直径,∴.
由已知知 ,∴,
∴ . …………分
∴. ②
∴由①②可知:,
∴. …………6分
(Ⅱ)由(Ⅰ)知: ,∴,,
∴是二面角的平面角 . …………8分
, , .
∴ .
. ………12分
(解法二):建立如图所示的直角坐标系,
由题意可知.解得.
则,,, ,
∵是的中点,
∴ 可求得. …………3分
(Ⅰ),,
∴.
∵,
∴. …………6分
(Ⅱ)由(Ⅰ)知,, ,
, .
∵,.∴是平面的法向量. ……8分
设是平面的法向量,由,,
解得 ………10分
.
所以二面角的平面角的余弦值. …………12分]
如图所示,该几何体是由一个直三棱柱和一个四棱锥组合而成,其中,,.
(Ⅰ)证明:平面;
(Ⅱ)若四棱锥的高2,求二面角的余弦值.[endnoteRef:16]
[16: 答案:;
(Ⅰ)证明:直三棱柱中,平面,……………… 2分
所以,又,,……………… 3分
所以平面. ……………… 4分
(Ⅱ)由(Ⅰ)知平面,以为原点,,,方向为,,轴建立空间直角坐标系(如图所示),,则,,,,,,.……………… 6分
设平面的一个法向量,
则取,则,
所以.……………… 8分
设平面的一个法向量,则
取,则,,所以.……………… 10分
所以……………… 11分
因为二面角的平面角是锐角,
所以所求二面角的余弦值为.……………… 12分
]
如图,直角梯形中,,等腰梯形中,,且平面平面.
(1)求证:平面;
(2)若与平面所成角为,求二面角的余弦值.[endnoteRef:17]
[17: 答案:;
解:(1)∵平面平面,,平面平面,
∴平面,又平面,∴,
又∵,且,∴平面;
(2)设,∵四边形为等腰梯形,,
∴,
∵,∴四边形为平行四边形,∴,
又∵平面,∴平面,
∴为与平面所成的角,∴,
又∵,∴,
以为原点,为轴,为轴,为轴,建立空间直角坐标系,
则,,∵平面,∴平面的法向量为,
设平面的一个法向量为,
由得,令得,,
,∴二面角的余弦值为.]
《空间向量》专题12-8 二面角(中档)
如图,在直角梯形中,,且分别为的中点,沿把折起,使,得到如下的立体图形.
(1)证明:平面平面;
(2)若,求二面角的大小.[endnoteRef:18]
[18: 答案:;
(1)证明:有题可得,则,
又,且,所以平面,
因为平面,所以平面平面,
(2)解:过点作交于点,连接,则平面,.
又,所以平面.
易得,则,得.
以为坐标原点,为轴,为轴,为轴,建立如图所示的空间直角坐标系,则.
故.
设是平面的法向量,则
令得.
设是平面的法向量,则同理.
因为,所以二面角为.
]
如图,四棱柱的底面为菱形,且.
(1)证明:四边形为矩形;
(2)若,与平面所成的角为,求二面角的余弦值.[endnoteRef:19]
[19: 答案:;
(1)证明:连接,设,连接.
∵,∴.
又为的中点,∴..
∴平面,∴.
∵,∴.
又四边形是平行四边形,则四边形为矩形.
(2)解:过点作平面,垂足为,由已知可得点在上,∴.
设,则.
在菱形中,,∴.
∴点与点重合,则平面.
以为坐标原点,建立空间直角坐标系.
则.
∴.
设平面的法向量为,则 ,∴即
取,可得为平面的一个法向量.
同理可得平面的一个法向量为。
∵.所以二面角的余弦值为.
]
(8套,8页,含答案)
如图,在三棱台ABC-DEF中,二面角B-AD-C是直二面角,AB⊥AC,AB=3,.
(1)求证:AB⊥平面ACFD;
(2)求二面角F-BE-D的平面角的余弦值[endnoteRef:0].
[0: 答案:;
(1)连接,在等腰梯形中,过作交于点,因为,所以,,,所以,所以,即, 2分
又二面角是直二面角,平面,所以平面, 4分
又平面,所以,又因为,,、平面,所以平面. 6分
(2)如图,在平面内,过点作,由(1)可知,以为原点,,,的方向为轴,轴,轴的正方向,建立空间直角坐标系.
则,,,, 7分
所以,,设是平面的一个法向量,则,所以,
取,则,,
即, 9分
由(1)可知平面,
所以是平面的一个法向量, 10分
所以, 11分
又二面角的平面角为锐角,
所以二面角的平面角的余弦值为. 12分]
如图,在梯形ABCD中,AB//CD,AD=DC=CB=2,∠ABC=60°,平面ACEF⊥平面ABCD,四边形ACEF是菱形,∠CAF=60°.
(1)求证:BF⊥AE;
(2)求二面角B-EF-D的平面角的正切值.([endnoteRef:1])
[1: 答案:;
【解析】(1)依题意,在等腰梯形中,,,
∵,∴,即,·········1分
∵平面平面,∴平面,·········2分
而平面,∴.·········3分
连接,∵四边形是菱形,∴,·········4分
∴平面,
∵平面,∴.·········6分
(2)取的中点,连接,因为四边形是菱形,且.
所以由平面几何易知,∵平面平面,∴平面.
故此可以、、分别为、、轴建立空间直角坐标系,各点的坐标依次为:,,,,,.······7分
设平面和平面的法向量分别为,,
∵,.
∴由,令,则,··9分
同理,求得.·········10分
∴,故二面角的平面角的正切值为.·······12分
]
已知四棱锥S-ABCD,SA⊥平面ABCD,底面ABCD为直角梯形,AB//DC,∠DAB=90°,
AB=2DC,,M是SB中点.
(1)求证:CM//平面SAD;
(2)若直线DM与平面SAB所成角的正切值为,F是SC的中点,求二面角C-AF-D的余弦值.([endnoteRef:2])
[2: 答案:;
【解析】(1)证明:取中点,连接,,
在中,,,,,
四边形为平行四边形.·········2分
,·········3分
又平面,平面,
平面.·········4分
(2)由已知得:,,两两垂直,以,,所在直线分别为轴,轴,轴建立如图所示的空间直角坐标系.·········5分
,,,平面,
就是与平面所成的角.
在中,,即,·········7分
设,则,,;
中,为斜边中点,,
.
则,,,,,
所以,,.
设是平面的一个法向量,则
,
令,得.·········9分
设是平面的一个法向量,则
,
令,.·········11分
.
二面角的余弦值为.·········12分]
《空间向量》专题12-2 二面角(中档)
在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB//CD,AB⊥AD,O为AD中点,,AD=AB=2CD=2.
求证:平面POB⊥平面PAC;
求二面角A-PC-D的余弦值.[endnoteRef:3]
[3: 答案:;
证明:由条件可知,,,
,.
,且为中点,.
,平面.
又平面,.
又,平面.
平面,平面平面.
解:以为空间坐标原点,建立如图所示的空间直角坐标系,则,,,,,,,,
设为平面的一个法向量,
由得,解得.
令,则.
同理可得,平面的一个法向量,
二面角的平面角的余弦值.
]
如图,在几何体ABCDEF中,底面CDEF是平行四边形,AB//CD,,DB⊥平面CDEF,CE与DF交于点O.
(1)求证:OB//平面ACF;
(2)若平面CAF与平面DAF所成的锐二面角余弦值为,求线段DB的长度.[endnoteRef:4]
[4: 答案:或;
解:(Ⅰ)取中点,连接,
在中,是的中点,是的中点,
所以,
又,
所以
所以四边形为平行四边形,
所以,
又因为平面,平面,
故平面.
(Ⅱ)由,,
可得,所以,
又平面,故以为坐标原点,直线分别为轴建立如图所示的空间直角坐标系,则,,,设,则,,
所以,,.
设平面的一个法向量,
则即,
取得,
设平面的一个法向量,
则即,
取得,
设平面与平面所成的锐二面角为,
则,
整理得,
解得或,
所以或.
]
《空间向量》专题12-3 二面角(中档)
如图,四棱锥P-ABCD中,PA⊥底面ABCD,ABCD为直角梯形,AD//BC,AD⊥AB,,AC∩BD=O,过O点作平面α平行于平面PAB,平面α与棱BC,AD,PD,PC分别相交于点E,F,G,H.
(1)求GH的长度;
(2)求二面角B-FH-E的余弦值.[endnoteRef:5]
[5: 答案:,;
解:(Ⅰ)【法一】(Ⅰ)因为平面,平面平面,
,平面平面,所以,同理,
因为∥,所以∽,且,
所以,,
同理,连接,则有∥,
所以,,所以,同理,,
过点作∥交于,则
【法二】因为平面,平面平面,,
平面平面,
根据面面平行的性质定理,所以,同理,
因为,所以,且,
又因为∽,,所以,
同理,,
如图:作,
所以,故四边形为矩形,即,
在中,所以,所以.
(Ⅱ)建立如图所示空间直角坐标系,
, 设平面的法向量为,
,令,得,
因为平面平面,所以平面的法向量
,二面角的余弦值为.
]
如图,在四棱柱ABCD-A1B1C1D1中,AB//CD,AB=BC=CC1=2CD,E为线段AB的中点,F是线段DD1上的动点.
(Ⅰ)求证:EF∥平面BCC1B1
(Ⅱ)若∠BCD=∠C1CD=60°,且平面D1C1CD⊥平面ABCD,求平面BCC1B1与DC1B1平面所成角(锐角)的余弦值.[endnoteRef:6]
[6: 答案:;
证明:(1)连结DE,D1E,∵AB∥CD,AB=2CD,E是AB的中点,
∴BE∥CD,BE=CD, ∴四边形BCDE是平行四边形,
∴DE∥BC,又DE平面BCC1B1,
∴DE∥平面BCC1B1, 同理D1D∥平面BCC1B1,又D1D∩DE=D,
∴平面DED1∥平面BCC1B1, ∵EF平面DED1,
∴EF∥平面BCC1B1. ................6分
方法一(2)∵AB=BC=CC1=2CD,∠BCD=∠C1CD=60°,
设CD=1,则BC=2,BD2=3 ∴BD⊥CD. 同理:C1D⊥CD,
∵平面D1C1CD⊥平面ABCD,平面D1C1CD∩平面ABCD=CD,C1D平面D1C1CD,
∴C1D⊥平面ABCD, ∴C1D⊥BC.∴C1D⊥B1C1
在平面ABCD中,过D作DH⊥BC,垂足为H,连结C1H.
∴BC⊥平面C1DH,∵C1H平面C1DH,
∴BC⊥C1H, 所以,B1C1⊥C1H,
∴∠DC1H为平面BCC1B1与DC1B1平面所成的角.
在Rt△BCD中, C1D=, 在Rt△C1DH,C1H=,∴cos∠DC1H=
∴平面BCC1B1与DC1B1平面所成的角(锐角)的余弦值为 ................12分
方法二:可以建立空间坐标系解答,(略)]
如图,在三棱柱ABC-A1B1C1中,∠AA1B1=45°,AC=BC,平面BB1C1C⊥平面AA1B1B,E为CC1中点.
(1)求证:BB1⊥AC;
(2)若直线A1C1与平面ABB1A1所成角为45°,求平面A1B1E与平面ABC所成锐二面角的余弦值.[endnoteRef:7]
[7: 答案:;
【证明】(1)过点做交于,因为面 ,,
所以,故,………2分
又因为,所以,故,
因为,所以,又因为,所以面,
故.………5分
(2)以为坐标原点,所在直线为轴,建立空间直角坐标,
,
设面的法向量为, 则令,
得; ………7分
设面的法向量为,则令
得;………9分
………11分
面与面所成锐二面角的余弦值为.………12分
]
《空间向量》专题12-4 二面角(中档)
如图所示,该几何体是由一个直三棱柱ADE-BCF和一个四棱锥P-ABCD组合而成,其中.
(1)证明:AD⊥平面ABFE;
(2)若四棱锥P-ABCD的高2,求二面角C-AF-P的余弦值.[endnoteRef:8]
[8: 答案:;
(1)证明:直三棱柱中,平面,所以,
又,所以平面;
(2)解:由(1)知平面,以为原点,方向为轴建立空间直角坐标系(如图所示),,则,,,,,,,设平面的一个法向量,
则,取,则,所以.
设平面的一个法向量,则,取,则.
所以,所以,
因为二面角的平面角是锐角,所以所求二面角的余弦值为.
]
如图,三棱台ABC﹣A1B1C1中,侧面A1B1BA与侧面A1C1CA是全等的梯形,
若A1A⊥AB,A1A⊥A1C1,且AB=2A1B1=4A1A.
(Ⅰ)若,,证明:DE∥平面BCC1B1;
(Ⅱ)若二面角C1﹣AA1﹣B为,求平面A1B1BA与平面C1B1BC所成的锐二面角的余弦值.[endnoteRef:9]
[9: 答案:;
【解答】(Ⅰ)证明:连接AC1,BC1,
在梯形A1C1CA中,AC=2A1C1,
∵AC1∩A1C=D,,
∴,
又,∴DE∥BC1,
∵BC1 平面BCC1B1,DE 平面BCC1B1,
∴DE∥平面BCC1B1 ;
(Ⅱ)解:侧面A1C1CA是梯形,∵A1A⊥A1C1,∴AA1⊥AC,
又A1A⊥AB,∴∠BAC为二面角C1﹣AA1﹣B的平面角,则∠BAC=,
∴△ABC,△A1B1C1均为正三角形,
在平面ABC内,过点A作AC的垂线,如图建立空间直角坐标系,
不妨设AA1=1,则A1B1=A1C1=2,AC=AC=4,
故点A1(0,0,1),C(0,4,0),.
设平面A1B1BA的法向量为,
则有,取,得;
设平面C1B1BC的法向量为,
则有,取,得.
∴,
故平面A1B1BA与平面C1B1BC所成的锐二面角的余弦值为.
]
《空间向量》专题12-5 二面角(中档)
如图,正三棱柱ABC-A1B1C1的所有棱长均2,D为棱BB1(不包括端点)上一动点,E是AB的中点.
(Ⅰ)若AD⊥A1C,求BD的长;
(Ⅱ)当D在棱BB1(不含端点)上运动时,求平面ADC1与平面ABC的夹角的余弦值的取值范围.[endnoteRef:10] [10: 答案:(,];
证明:(Ⅰ),由AC=BC,AE=BE,知CE⊥AB,
又平面ABC⊥平面ABB1A1,所以CE⊥平面ABB1A1
而AD 平面ABB1A1,∴AD⊥CE,又AD⊥A1C所以AD⊥平面A1CE,
所以AD⊥A1E.易知此时D为BB1的中点,故BD=1.…………………5分
(Ⅱ)以E为原点,EB为x轴,EC为y轴,
过E作垂直于平面ABC的垂线为z轴,
建立空间直角坐标系,设 BD=t,
则A(-1,0,0),D(1,0,t),C1(0,,2),
=(2,0,t),=(1,,2),设平面ADC1的法向量=(x,y,z),
则,取x=1,得,
平面ABC的法向量=(0,0,1),设平面ADC1与平面ABC的夹角为θ,
∴cosθ====
由于t∈(0,2),故cosθ∈(,].
即平面ADC1与平面ABC的夹角的余弦值的取值范围为(,].………………12分]
菱形ABCD的对角线AC与BD交于点O,AB=2,AC=6,点E,F分别在AD,CD上,,EF交BD于点H,将△DEF沿EF折到△D′EF位置,.
(1)证明:D′H⊥平面ABCD;
(2)求二面角B-D′A-C的正弦值.[endnoteRef:11]
[11: 答案:;
解:(1)∵,
∴,∴,
∵四边形为菱形,
∴,
∴,∴,∴
∵,
∴;
又,,∴,∴,∴,
∴,∴,又∵,
∴平面.
(Ⅱ)建立如图所示的空间直角坐标系:
,
,
设平面的一个法向量为,
由得,取,
∴,同理可得平面的法向量为,
∴,∴.
]
如图,在三棱锥P-ABC中,平面PAB⊥平面ABC,AB=6,,,D,E分别为线段AB,BC上的点,且AD=2DB,CE=2EB,PD⊥AC.
(1)求证:PD⊥平面ABC;
(2)若PA与平面ABC所成的角为,求平面PAC与平面PDE所成的锐二面角.[endnoteRef:12]
[12: 答案:;
(1)证明:连接,由题意知
,则,...............2分
又因为,所以
因为,都在平面内,
所以平面 ;...............4分
(2)由(1)知两两互相垂直,建立如图所示的直角坐标系,
且与平面所成的角为,有,
则
∴
因为
由(1)知平面,∴ 平面...............8分
∴为平面的一个法向量.
设平面的法向量为,则
∴,令,则,...............10分
∴为平面的一个法向量.
∴
故平面与平面的锐二面角的余弦值为,
所以平面与平面的锐二面角为................12分]
《空间向量》专题12-6 二面角(中档)
如图,四棱锥的底面是平行四边形,,.
(1)求异面直线与所成的角;
(2)若,,,求二面角的余弦值.[endnoteRef:13]
[13: 答案:90°,;
解:(1)取中点,连接,可证面,
所以异面直线与所成的角为90°
(2)设,则,,又,可得.
由(1)知,从而平面,
以为坐标原点,的方向分别为轴建立坐标系.
则,,,,
,所以,
,,,
可求得平面的法向量,
平面的法向量,
所以
又二面角为锐角,故二面角的余弦值为.
]
如图,在四棱锥中,平面,底面是菱形,,为与的交点,为上任意一点.
(1)证明:平面平面;
(2)若平面,并且二面角的大小为,求的值.[endnoteRef:14]
[14: 答案:;
解:(1)因为平面,∴,
又是菱形,∴,故平面
∴平面平面.
(2)解:连结,因为平面,
所以,所以平面,
又是的中点,故此时为的中点,
以为坐标原点,射线分别为轴建立空间直角坐标系
设,则,
向量为平面的一个法向量
设平面的一个法向量为,
则且
即且,
取,则,,则
∴,解得
故.
]
《空间向量》专题12-7 二面角(中档)
如图,四边形是圆柱的轴截面,点在圆柱的底面圆周上,是的中点,圆柱的底面圆的半径,侧面积为,.
(Ⅰ)求证:;
(Ⅱ)求二面角的平面角的余弦值.([endnoteRef:15])
[15: 答案:;
解:(Ⅰ)(解法一):由题意可知 ,解得 ,……分
在中,, …………分
∴,又∵是的中点,∴. ① …………分
∵为圆的直径,∴.
由已知知 ,∴,
∴ . …………分
∴. ②
∴由①②可知:,
∴. …………6分
(Ⅱ)由(Ⅰ)知: ,∴,,
∴是二面角的平面角 . …………8分
, , .
∴ .
. ………12分
(解法二):建立如图所示的直角坐标系,
由题意可知.解得.
则,,, ,
∵是的中点,
∴ 可求得. …………3分
(Ⅰ),,
∴.
∵,
∴. …………6分
(Ⅱ)由(Ⅰ)知,, ,
, .
∵,.∴是平面的法向量. ……8分
设是平面的法向量,由,,
解得 ………10分
.
所以二面角的平面角的余弦值. …………12分]
如图所示,该几何体是由一个直三棱柱和一个四棱锥组合而成,其中,,.
(Ⅰ)证明:平面;
(Ⅱ)若四棱锥的高2,求二面角的余弦值.[endnoteRef:16]
[16: 答案:;
(Ⅰ)证明:直三棱柱中,平面,……………… 2分
所以,又,,……………… 3分
所以平面. ……………… 4分
(Ⅱ)由(Ⅰ)知平面,以为原点,,,方向为,,轴建立空间直角坐标系(如图所示),,则,,,,,,.……………… 6分
设平面的一个法向量,
则取,则,
所以.……………… 8分
设平面的一个法向量,则
取,则,,所以.……………… 10分
所以……………… 11分
因为二面角的平面角是锐角,
所以所求二面角的余弦值为.……………… 12分
]
如图,直角梯形中,,等腰梯形中,,且平面平面.
(1)求证:平面;
(2)若与平面所成角为,求二面角的余弦值.[endnoteRef:17]
[17: 答案:;
解:(1)∵平面平面,,平面平面,
∴平面,又平面,∴,
又∵,且,∴平面;
(2)设,∵四边形为等腰梯形,,
∴,
∵,∴四边形为平行四边形,∴,
又∵平面,∴平面,
∴为与平面所成的角,∴,
又∵,∴,
以为原点,为轴,为轴,为轴,建立空间直角坐标系,
则,,∵平面,∴平面的法向量为,
设平面的一个法向量为,
由得,令得,,
,∴二面角的余弦值为.]
《空间向量》专题12-8 二面角(中档)
如图,在直角梯形中,,且分别为的中点,沿把折起,使,得到如下的立体图形.
(1)证明:平面平面;
(2)若,求二面角的大小.[endnoteRef:18]
[18: 答案:;
(1)证明:有题可得,则,
又,且,所以平面,
因为平面,所以平面平面,
(2)解:过点作交于点,连接,则平面,.
又,所以平面.
易得,则,得.
以为坐标原点,为轴,为轴,为轴,建立如图所示的空间直角坐标系,则.
故.
设是平面的法向量,则
令得.
设是平面的法向量,则同理.
因为,所以二面角为.
]
如图,四棱柱的底面为菱形,且.
(1)证明:四边形为矩形;
(2)若,与平面所成的角为,求二面角的余弦值.[endnoteRef:19]
[19: 答案:;
(1)证明:连接,设,连接.
∵,∴.
又为的中点,∴..
∴平面,∴.
∵,∴.
又四边形是平行四边形,则四边形为矩形.
(2)解:过点作平面,垂足为,由已知可得点在上,∴.
设,则.
在菱形中,,∴.
∴点与点重合,则平面.
以为坐标原点,建立空间直角坐标系.
则.
∴.
设平面的法向量为,则 ,∴即
取,可得为平面的一个法向量.
同理可得平面的一个法向量为。
∵.所以二面角的余弦值为.
]
