第8单元总复习简易方程课件 五年级上册数学 人教版(共17张PPT)
文档属性
| 名称 | 第8单元总复习简易方程课件 五年级上册数学 人教版(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 424.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-26 16:10:05 | ||
图片预览





文档简介
(共17张PPT)
《简易方程复习课》
环节一 梳理回顾
新授主题图位置
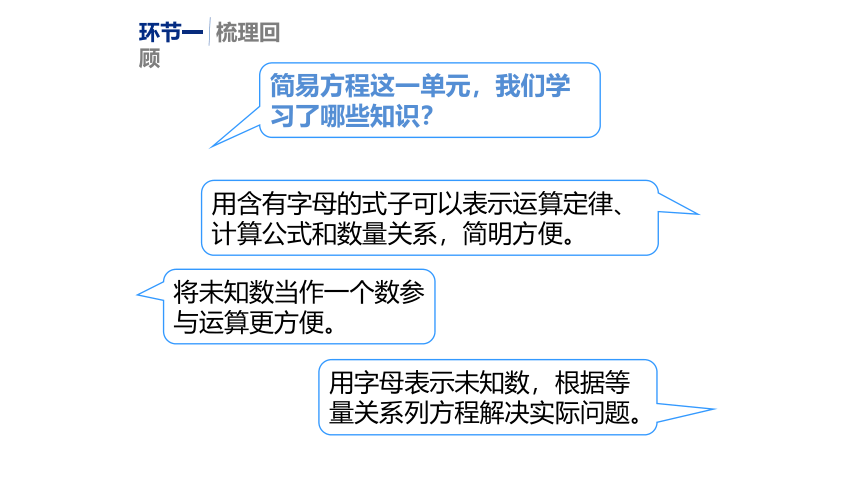
简易方程这一单元,我们学习了哪些知识?
将未知数当作一个数参与运算更方便。
用字母表示未知数,根据等量关系列方程解决实际问题。
用含有字母的式子可以表示运算定律、计算公式和数量关系,简明方便。
环节一 梳理回顾
新授主题图位置
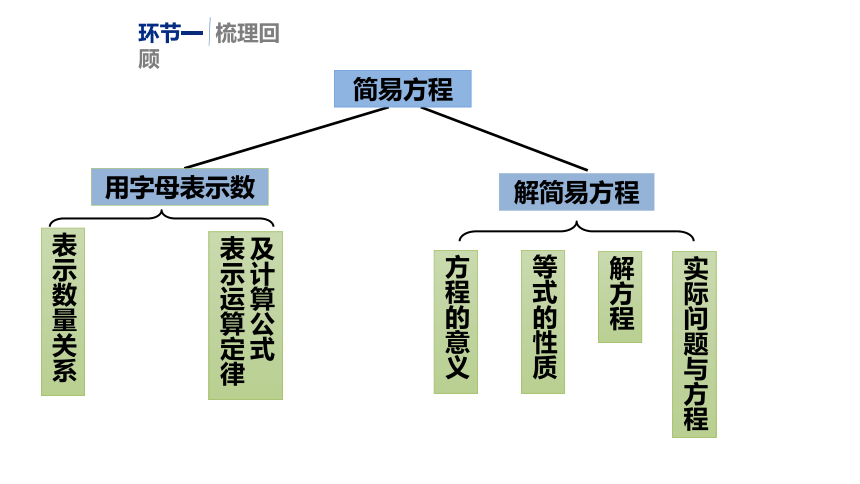
方程的意义
等式的性质
解方程
及计算公式
表示运算定律
表示数量关系
实际问题与方程
用字母表示数
解简易方程
简易方程
光每秒能传播30万千米,这个路程大约比地球赤道长度的7倍还多2万千米。地球赤道大约长多少万千米?
解:设地球赤道大约长x万千米
7x+2=30
7x+2-2=30-2
7x=28
环节一 梳理回顾
列方程解决问题第一步都是要干什么?
7x÷7=28÷7
x=4
答:地球赤道大约长4万千米。
环节二 复习巩固
1.用字母表示数
2.用字母表示数量关系。
一个数“比x 的4倍多13”,这个数怎样表示呢?
一、复习用字母表示数。
用字母可以表示一个具体的量,也可以表示一个数,那这个字母“x ”可以表示哪些数?
4x+13
这个含有字母的式子除了表示数,还可以表示什么?
环节二 复习巩固
3.练习。
2ɑ与2ɑ相加 ɑ+2b
2ɑ与2ɑ相乘 4ɑ
ɑ与b的和的2倍 4ɑ
ɑ与b的2倍的和 2(ɑ+b)
这些含有字母的式子分别表示什么?连一连。
环节二 复习巩固
二、复习方程与解方程
1.复习方程
(1)当x =5时,比x 的4倍多13这个数是多少呢?
(2)如果“比x 的4倍多13的数是45。”又该怎样表示?
(3)小组交流:
①什么叫方程?方程与等式有什么关系?举例说明。
②什么是解方程?什么是方程的解?
环节二 复习巩固
2.复习解方程。
解方程。
x÷1.44=0.4
解 :x÷1.44×1.44=0.4×1.44
x=0.576
3.85+1.5x=6.1
解:3.85+1.5x-3.85=6.1-3.85
1.5x=2.25
1.5x÷1.5=2.25÷1.5
6x-0.9=4.5
解:6x-0.9+0.9=4.5+0.9
6x=5.4
6x÷6=5.4÷6
我们解方程的依据是什么?
x=1.5
x=0.9
环节二 复习巩固
2.复习解方程。
如何判断未知数的值就是方程的解呢?
=6×0.9-0.9
=5.4-0.9
=4.5
=方程右边
所以,x=0.9是方程的解。
方程左边=6x-0.9
环节二 复习巩固
三、复习用方程解决问题
1.复习用方程解决问题的一般步骤
在这几步中你们认为哪一步是最关键的?
A.弄清题意,找出未知数用X表示。
B.分析、找出等量关系,列方程。
C.解方程。
D.检验写答语。
环节二 复习巩固
2.复习数量关系
(1)请你们找出它们的等量关系,并说出方程。
②小明买了8个作业本,每本x 元,付给营业员5元,
找回2.6元。
① 一个梯形的面积是265平方米,上底是20米,下底是33米,高x 米。
计算公式也是一种数量关系。
环节二 复习巩固
(2)下面请根据方程选择合适的条件,并和同桌说一说你的你的想法。
2.复习数量关系
甲筐有桔子60千克,( ),乙筐有桔子多少千克?
设:乙筐有桔子X 千克。
2X +4=60
①甲筐比乙筐的2倍还多4千克 ②乙筐比甲筐的一半少4千克
③乙筐比甲筐的2倍还多4千克 ④甲筐比乙筐的一半少4千克
环节二 复习巩固
一条公路长360m,甲、乙两支施工队同时从公路的两端往中间铺柏油。甲队的施工速度是乙队的1.25倍,4天后这条公路全部铺完。甲、乙两队每天分别铺泊油路多少米
解:设乙队每天铺柏油路x m,则甲队每天铺柏油路1.25x m。
4×(1.25x+x)=360
x=40
1.25×40=50(m)
答:甲、乙两队每天分别铺泊油路50 m,40 m。
1.请用字母表示下面的数量关系。
王叔叔每小时加工a个零件,t小时共加工c个零件。
①如果每小时加工30个零件,5小时可以加工( )个零件。
②如果每小时加工25个零件,( )小时可以加工100个零件。
at=c
150
4
2.一个玩具厂做一个毛绒兔原来需要3.8元的材料。后来改进了制作方法,每个只需要3.6元的材料。原来准备做180个毛绒兔的材料,现在可以做多少个?
答:现在可以做190个。
解:设现在可以做x个。
3.6x=3.8×180
x=190
3.6x=144
3.6x÷3.6=144÷3.6
3.某地举行长跑比赛,运动员跑到离起点3km处要返回起跑点。领先的运动员每分钟跑310m,最后的运动员每分钟跑290m。起跑后多少分钟这两个运动员相遇?相遇时离返回点有多少米?
3000×2÷(310+290)
=6000÷600
=10(分钟)
3km=3000m
3000-290×10
=3000-2900
=100(米)
答:起跑后10分钟这两个运动员相遇,相遇时离返回点有100米。
4.一座大桥长2400M,一列火车以每分钟900M的速度通过大桥,从车头开上桥到车尾离开桥共需3分钟。这列火车长多少米?
5.甲种茶叶每千克240元,乙种茶叶每千克180元,丙种茶叶每千克150元,如果用5千克甲种茶叶,3千克乙种茶叶和若干丙种茶叶混成每千克190元的混合茶叶,需要多少千克丙种茶叶?
拓展练习:
《简易方程复习课》
环节一 梳理回顾
新授主题图位置
简易方程这一单元,我们学习了哪些知识?
将未知数当作一个数参与运算更方便。
用字母表示未知数,根据等量关系列方程解决实际问题。
用含有字母的式子可以表示运算定律、计算公式和数量关系,简明方便。
环节一 梳理回顾
新授主题图位置
方程的意义
等式的性质
解方程
及计算公式
表示运算定律
表示数量关系
实际问题与方程
用字母表示数
解简易方程
简易方程
光每秒能传播30万千米,这个路程大约比地球赤道长度的7倍还多2万千米。地球赤道大约长多少万千米?
解:设地球赤道大约长x万千米
7x+2=30
7x+2-2=30-2
7x=28
环节一 梳理回顾
列方程解决问题第一步都是要干什么?
7x÷7=28÷7
x=4
答:地球赤道大约长4万千米。
环节二 复习巩固
1.用字母表示数
2.用字母表示数量关系。
一个数“比x 的4倍多13”,这个数怎样表示呢?
一、复习用字母表示数。
用字母可以表示一个具体的量,也可以表示一个数,那这个字母“x ”可以表示哪些数?
4x+13
这个含有字母的式子除了表示数,还可以表示什么?
环节二 复习巩固
3.练习。
2ɑ与2ɑ相加 ɑ+2b
2ɑ与2ɑ相乘 4ɑ
ɑ与b的和的2倍 4ɑ
ɑ与b的2倍的和 2(ɑ+b)
这些含有字母的式子分别表示什么?连一连。
环节二 复习巩固
二、复习方程与解方程
1.复习方程
(1)当x =5时,比x 的4倍多13这个数是多少呢?
(2)如果“比x 的4倍多13的数是45。”又该怎样表示?
(3)小组交流:
①什么叫方程?方程与等式有什么关系?举例说明。
②什么是解方程?什么是方程的解?
环节二 复习巩固
2.复习解方程。
解方程。
x÷1.44=0.4
解 :x÷1.44×1.44=0.4×1.44
x=0.576
3.85+1.5x=6.1
解:3.85+1.5x-3.85=6.1-3.85
1.5x=2.25
1.5x÷1.5=2.25÷1.5
6x-0.9=4.5
解:6x-0.9+0.9=4.5+0.9
6x=5.4
6x÷6=5.4÷6
我们解方程的依据是什么?
x=1.5
x=0.9
环节二 复习巩固
2.复习解方程。
如何判断未知数的值就是方程的解呢?
=6×0.9-0.9
=5.4-0.9
=4.5
=方程右边
所以,x=0.9是方程的解。
方程左边=6x-0.9
环节二 复习巩固
三、复习用方程解决问题
1.复习用方程解决问题的一般步骤
在这几步中你们认为哪一步是最关键的?
A.弄清题意,找出未知数用X表示。
B.分析、找出等量关系,列方程。
C.解方程。
D.检验写答语。
环节二 复习巩固
2.复习数量关系
(1)请你们找出它们的等量关系,并说出方程。
②小明买了8个作业本,每本x 元,付给营业员5元,
找回2.6元。
① 一个梯形的面积是265平方米,上底是20米,下底是33米,高x 米。
计算公式也是一种数量关系。
环节二 复习巩固
(2)下面请根据方程选择合适的条件,并和同桌说一说你的你的想法。
2.复习数量关系
甲筐有桔子60千克,( ),乙筐有桔子多少千克?
设:乙筐有桔子X 千克。
2X +4=60
①甲筐比乙筐的2倍还多4千克 ②乙筐比甲筐的一半少4千克
③乙筐比甲筐的2倍还多4千克 ④甲筐比乙筐的一半少4千克
环节二 复习巩固
一条公路长360m,甲、乙两支施工队同时从公路的两端往中间铺柏油。甲队的施工速度是乙队的1.25倍,4天后这条公路全部铺完。甲、乙两队每天分别铺泊油路多少米
解:设乙队每天铺柏油路x m,则甲队每天铺柏油路1.25x m。
4×(1.25x+x)=360
x=40
1.25×40=50(m)
答:甲、乙两队每天分别铺泊油路50 m,40 m。
1.请用字母表示下面的数量关系。
王叔叔每小时加工a个零件,t小时共加工c个零件。
①如果每小时加工30个零件,5小时可以加工( )个零件。
②如果每小时加工25个零件,( )小时可以加工100个零件。
at=c
150
4
2.一个玩具厂做一个毛绒兔原来需要3.8元的材料。后来改进了制作方法,每个只需要3.6元的材料。原来准备做180个毛绒兔的材料,现在可以做多少个?
答:现在可以做190个。
解:设现在可以做x个。
3.6x=3.8×180
x=190
3.6x=144
3.6x÷3.6=144÷3.6
3.某地举行长跑比赛,运动员跑到离起点3km处要返回起跑点。领先的运动员每分钟跑310m,最后的运动员每分钟跑290m。起跑后多少分钟这两个运动员相遇?相遇时离返回点有多少米?
3000×2÷(310+290)
=6000÷600
=10(分钟)
3km=3000m
3000-290×10
=3000-2900
=100(米)
答:起跑后10分钟这两个运动员相遇,相遇时离返回点有100米。
4.一座大桥长2400M,一列火车以每分钟900M的速度通过大桥,从车头开上桥到车尾离开桥共需3分钟。这列火车长多少米?
5.甲种茶叶每千克240元,乙种茶叶每千克180元,丙种茶叶每千克150元,如果用5千克甲种茶叶,3千克乙种茶叶和若干丙种茶叶混成每千克190元的混合茶叶,需要多少千克丙种茶叶?
拓展练习:
