沪科版物理九年级全册课课练:专题训练 欧姆定律的综合计算(含答案)
文档属性
| 名称 | 沪科版物理九年级全册课课练:专题训练 欧姆定律的综合计算(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 185.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-07-26 00:00:00 | ||
图片预览


文档简介
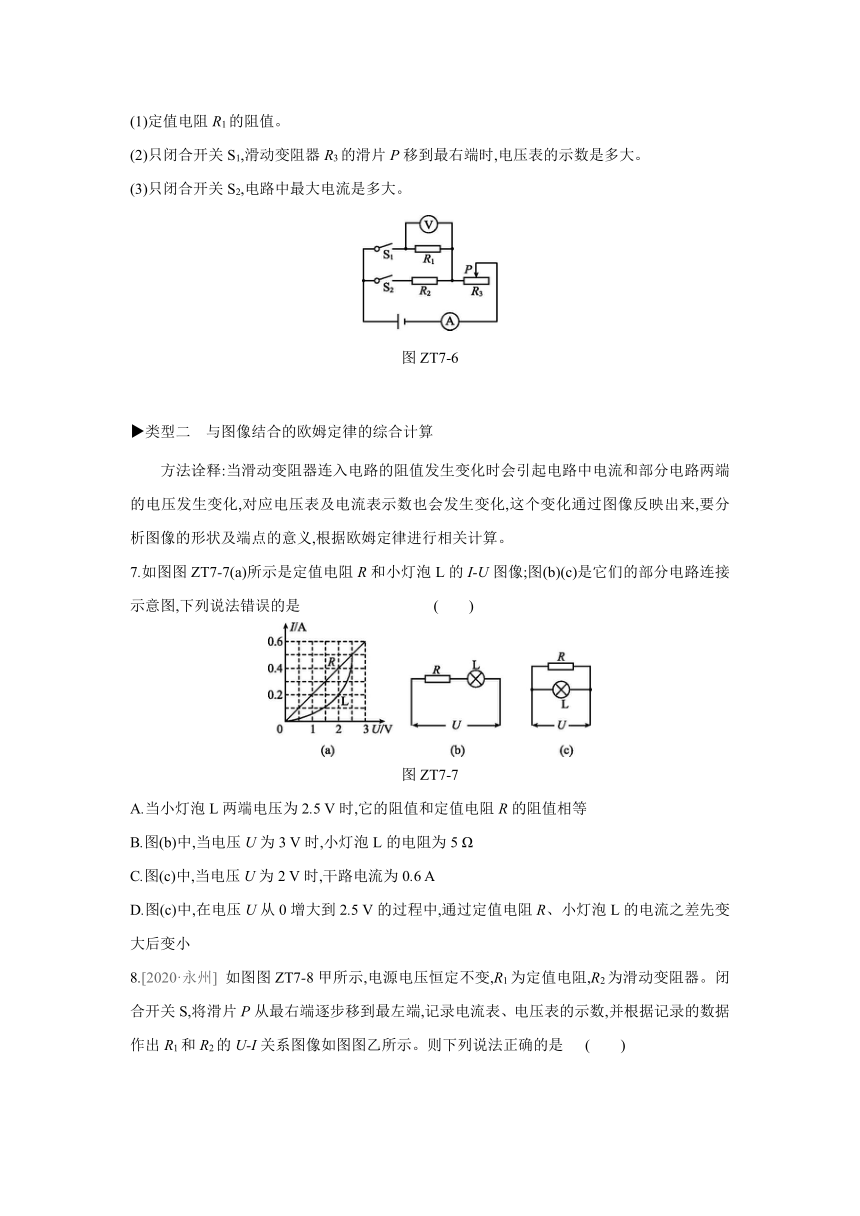
专题训练
[欧姆定律的综合计算]
类型一 动态电路中欧姆定律的综合计算
(一)开关引起的动态电路的计算
方法诠释:首先根据开关的闭合与断开判断电路的连接情况,画出等效电路图,然后确定各电表的测量对象,根据串、并联电路中电压、电流和电阻之间的关系结合欧姆定律进行计算。
1.如图图ZT7-1所示,R2=20 Ω,电源电压为15 V且不变。当S1、S2都断开时,电流表的示数为0.6 A,当S1、S2都闭合时,电流表的示数为4 A,则R1、R3的阻值分别为 ( )
图ZT7-1
A.5 Ω,15 Ω B.5 Ω,10 Ω C.25 Ω,10 Ω D.0.2 Ω,15 Ω
2.[2020·龙东] 如图图ZT7-2所示,电源电压保持不变,电阻R1=R2=R3=10 Ω,要使R2、R3并联,且两端电压等于电源电压,应闭合开关 ,此时电流表的示数为I1;要使R1、R2串联,应断开开关S1、S2,此时电流表的示数为I2;则I1∶I2= 。
图ZT7-2
3.如图图ZT7-3所示的电路中,电源电压是12 V且保持不变,R1=R3=4 Ω,R2=6 Ω。求:
(1)当开关S1、S2断开时,电流表和电压表示数各是多少。
(2)当开关S1、S2均闭合时,电流表和电压表示数各是多少。
图ZT7-3
(二)滑动变阻器引起的动态电路的计算
方法诠释:首先要理解滑动变阻器的铭牌标示的电阻为最大阻值,标示的电流为允许通过的最大电流;然后分析电路中电流、电压、电阻之间的变化情况,当滑动变阻器连入电路的电阻最小时,电路中所对应的电流为最大值;当滑动变阻器连入电路的电阻最大时,电路中所对应的电流为最小值。
4.[2020·云南] 如图图ZT7-4所示的电路,电源电压为6 V恒定不变,R1阻值为15 Ω,电流表的量程为0~0.6 A。
(1)开关S、S1都闭合,滑片P不能移到a端的原因是会造成电路 (选填“通路”“短路”或“开路”)。
(2)开关S闭合、S1断开时,求电流表的示数。
(3)开关S、S1都闭合时,为了电流表不超量程,求变阻器R2连入电路的最小阻值。
图ZT7-4
5.[2020·眉山] 如图图ZT7-5甲所示,R1为定值电阻,R2为滑动变阻器,电源电压保持不变,闭合开关S后,滑片P从a端滑到b端,电流表示数I与电压表示数U的变化关系如图图乙所示。求电源电压。
图ZT7-5
6.如图图ZT7-6所示电路,电源电压保持不变,已知定值电阻R2的阻值为10 Ω,滑动变阻器R3上标有“30 Ω 1 A”字样。当滑动变阻器R3的滑片P移到最左端,闭合开关S1、S2时,电压表的示数为3 V,电流表的示数为0.5 A。求:
(1)定值电阻R1的阻值。
(2)只闭合开关S1,滑动变阻器R3的滑片P移到最右端时,电压表的示数是多大。
(3)只闭合开关S2,电路中最大电流是多大。
图ZT7-6
类型二 与图像结合的欧姆定律的综合计算
方法诠释:当滑动变阻器连入电路的阻值发生变化时会引起电路中电流和部分电路两端的电压发生变化,对应电压表及电流表示数也会发生变化,这个变化通过图像反映出来,要分析图像的形状及端点的意义,根据欧姆定律进行相关计算。
7.如图图ZT7-7(a)所示是定值电阻R和小灯泡L的I-U图像;图(b)(c)是它们的部分电路连接示意图,下列说法错误的是 ( )
图ZT7-7
A.当小灯泡L两端电压为2.5 V时,它的阻值和定值电阻R的阻值相等
B.图(b)中,当电压U为3 V时,小灯泡L的电阻为5 Ω
C.图(c)中,当电压U为2 V时,干路电流为0.6 A
D.图(c)中,在电压U从0增大到2.5 V的过程中,通过定值电阻R、小灯泡L的电流之差先变大后变小
8.[2020·永州] 如图图ZT7-8甲所示,电源电压恒定不变,R1为定值电阻,R2为滑动变阻器。闭合开关S,将滑片P从最右端逐步移到最左端,记录电流表、电压表的示数,并根据记录的数据作出R1和R2的U-I关系图像如图图乙所示。则下列说法正确的是 ( )
图ZT7-8
A.图Ⅱ为R2的U-I关系图像
B.当R2=R1时,电流的大小为0.2 A
C.电源电压为8 V
D.R1的阻值为30 Ω
9.有一种由酒精气体传感器制成的呼气酒精测试仪被广泛用来检测酒驾,传感器R1的阻值随酒精气体浓度的变化如图图ZT7-9甲所示,工作电路如图图乙所示,电源电压恒为12 V,定值电阻R2=30 Ω。求:
(1)被检测者未喝酒时,R1的阻值。
(2)被检测者酒精气体浓度为0.8 mg/mL时,电流表的示数。
(3)现在公认的酒驾标准为0.2 mg/mL≤酒精气体浓度≤0.8 mg/mL,当电压表示数为4.8 V时,通过计算说明被检测司机是否属于酒驾。
图ZT7-9
答案
1.A
2.S1、S2 4∶1 要使电阻R2、R3并联,则电阻R2、R3中必须有电流通过,所以应闭合开关S1、S2,此时电流表测干路电流,因并联电路中总电阻的倒数等于各分电阻倒数之和,所以,电路中的总电阻:
R===5 Ω,
此时电流表的示数:I1== Ω;
断开开关S1、S2时,R1、R2串联,电流表测电路中的电流,因串联电路中总电阻等于各分电阻之和,所以,此时电流表的示数:I2===,
所以,I1∶I2=∶=4∶1。
3.(1)当开关S1、S2断开时,电阻R2与R3串联,电流表的示数:I1===1.2 A;电压表的示数:U1=I1R2=1.2 A×6 Ω=7.2 V。
(2)当开关S1、S2均闭合时,电阻R1与R2并联,电压表的示数为电源电压,为12 V;
电路总电阻:R===2.4 Ω,
电流表的示数:I===5 A。
4.(1)短路
(2)开关S闭合、S1断开时,电路为R1的简单电路,由欧姆定律知,电流表示数:I===0.4 A。
(3)开关S、S1都闭合时,电流表测干路电流,通过R1的电流为0.4 A不变,故通过变阻器的最大电流为I2=I最大-I=0.6 A-0.4 A=0.2 A,由欧姆定律可得,变阻器R2连入电路的最小阻值:R2===30 Ω。
5.由图甲知,R1与R2串联,电压表测R2两端的电压,电流表测电路中的电流。当滑片P在a端时,只有R1连入电路中,此时电路中电流最大,由图乙知,I1=0.6 A,由欧姆定律可得,电源电压:U=I1R1=0.6 A×R1①;当滑片P在b端时,R2(接入电路的电阻最大)与R1串联,电路中电流最小,由图乙知,I2=0.2 A,电压表示数为:UV=2 V,根据串联电路的规律及欧姆定律可得,电源电压:U=I2R1+UV=0.2 A×R1+2 V②,由①②得:R1=5 Ω,代入①得:电源电压:U=3 V。
6.(1)当滑动变阻器R3的滑片P移到最左端,闭合开关S1、S2时,电阻R1、R2并联,电压表测量电源电压,即电源电压为3 V,电流表测量干路电流;因为并联电路各支路两端电压相等且等于电源电压,所以U1=U2=U=3 V,通过R2的电流为I2===0.3 A,根据并联电路干路电流等于各支路电流之和知,通过R1的电流为I1=I-I2=0.5 A-0.3 A=0.2 A,R1的阻值为R1===15 Ω。
(2)只闭合开关S1,滑动变阻器R3的滑片P移到最右端时,R1与R3(接入电路的电阻最大)串联,电压表测R1两端的电压,此时电路中的电流为I'=== A,R1两端的电压为U1'=I'R1= A×15 Ω=1 V,即电压表的示数为1 V。
(3)只闭合开关S2时,R2与R3串联,当滑动变阻器接入电路的电阻为0时,电路中电流最大,最大电流为I最大===0.3 A。
7.B 由图(a)可知,当R、L两端电压均为2.5 V时,通过两者的电流均为0.5 A,则由I=的变形式R=可知,R、L的阻值相等,故A正确;图(b)中,R与L串联,由图(a)可知,当电路中的电流I=0.2 A、UR=1 V、UL=2 V时,电压U为3 V,此时L的电阻RL===10 Ω,故B错误;图(c)中,R与L并联,由图(a)可知,当电压U=2 V、IR=0.4 A、IL=0.2 A时,干路电流为0.6 A,故C正确;图(c)中,R与L并联,由图(a)可知,在电压U从0增大到2.5 V的过程中,通过R、L的电流之差先变大后变小,故D正确。
8.C 由图甲知,R1与R2串联,电压表V1测R1两端的电压,电压表V2测R2两端的电压,滑片在最左端时,R2接入电路的阻值为零,此时电压表V2示数为零,由图像可得,图线I反映电压表V2示数(即R2两端的电压)随电流的变化,则图线Ⅱ为R1的U-I关系图像,故A错误;串联电路中各处的电流相等,当R2=R1时,由U=IR可知,两电阻两端的电压相同,由图乙知,即为两图线的交点,可知电流为0.4 A,B错误;由图乙知,当电流为0.4 A时,两电压表示数均为4 V,则电源电压U=4 V+4 V=8 V,C正确;当滑片移动到最左端时,电路中只有R1,电压表V2示数为0,电路中电流为0.8 A,由欧姆定律可得,R1===10 Ω,D错误。
9.(1)由图甲可知,当被检测者未喝酒时,即酒精气体浓度为0时,R1的电阻为60 Ω。
(2)由图甲可知,当酒精气体浓度为0.8 mg/mL时,R1的电阻为10 Ω,
则R总=R1'+R2=10 Ω+30 Ω=40 Ω,
此时电路中电流:I===0.3 A,
即电流表的示数为0.3 A。
(3)当电压表的示数U1=4.8 V时,
则U2=U-U1=12 V-4.8 V=7.2 V,
电路中的电流:I1=I2===0.24 A,
此时传感器R1的阻值:R1″===20 Ω。
由图甲可知,被检测者的酒精气体浓度为0.3 mg/mL,因0.2 mg/mL<0.3 mg/mL<0.8 mg/mL,所以被检测者属于酒驾。
[欧姆定律的综合计算]
类型一 动态电路中欧姆定律的综合计算
(一)开关引起的动态电路的计算
方法诠释:首先根据开关的闭合与断开判断电路的连接情况,画出等效电路图,然后确定各电表的测量对象,根据串、并联电路中电压、电流和电阻之间的关系结合欧姆定律进行计算。
1.如图图ZT7-1所示,R2=20 Ω,电源电压为15 V且不变。当S1、S2都断开时,电流表的示数为0.6 A,当S1、S2都闭合时,电流表的示数为4 A,则R1、R3的阻值分别为 ( )
图ZT7-1
A.5 Ω,15 Ω B.5 Ω,10 Ω C.25 Ω,10 Ω D.0.2 Ω,15 Ω
2.[2020·龙东] 如图图ZT7-2所示,电源电压保持不变,电阻R1=R2=R3=10 Ω,要使R2、R3并联,且两端电压等于电源电压,应闭合开关 ,此时电流表的示数为I1;要使R1、R2串联,应断开开关S1、S2,此时电流表的示数为I2;则I1∶I2= 。
图ZT7-2
3.如图图ZT7-3所示的电路中,电源电压是12 V且保持不变,R1=R3=4 Ω,R2=6 Ω。求:
(1)当开关S1、S2断开时,电流表和电压表示数各是多少。
(2)当开关S1、S2均闭合时,电流表和电压表示数各是多少。
图ZT7-3
(二)滑动变阻器引起的动态电路的计算
方法诠释:首先要理解滑动变阻器的铭牌标示的电阻为最大阻值,标示的电流为允许通过的最大电流;然后分析电路中电流、电压、电阻之间的变化情况,当滑动变阻器连入电路的电阻最小时,电路中所对应的电流为最大值;当滑动变阻器连入电路的电阻最大时,电路中所对应的电流为最小值。
4.[2020·云南] 如图图ZT7-4所示的电路,电源电压为6 V恒定不变,R1阻值为15 Ω,电流表的量程为0~0.6 A。
(1)开关S、S1都闭合,滑片P不能移到a端的原因是会造成电路 (选填“通路”“短路”或“开路”)。
(2)开关S闭合、S1断开时,求电流表的示数。
(3)开关S、S1都闭合时,为了电流表不超量程,求变阻器R2连入电路的最小阻值。
图ZT7-4
5.[2020·眉山] 如图图ZT7-5甲所示,R1为定值电阻,R2为滑动变阻器,电源电压保持不变,闭合开关S后,滑片P从a端滑到b端,电流表示数I与电压表示数U的变化关系如图图乙所示。求电源电压。
图ZT7-5
6.如图图ZT7-6所示电路,电源电压保持不变,已知定值电阻R2的阻值为10 Ω,滑动变阻器R3上标有“30 Ω 1 A”字样。当滑动变阻器R3的滑片P移到最左端,闭合开关S1、S2时,电压表的示数为3 V,电流表的示数为0.5 A。求:
(1)定值电阻R1的阻值。
(2)只闭合开关S1,滑动变阻器R3的滑片P移到最右端时,电压表的示数是多大。
(3)只闭合开关S2,电路中最大电流是多大。
图ZT7-6
类型二 与图像结合的欧姆定律的综合计算
方法诠释:当滑动变阻器连入电路的阻值发生变化时会引起电路中电流和部分电路两端的电压发生变化,对应电压表及电流表示数也会发生变化,这个变化通过图像反映出来,要分析图像的形状及端点的意义,根据欧姆定律进行相关计算。
7.如图图ZT7-7(a)所示是定值电阻R和小灯泡L的I-U图像;图(b)(c)是它们的部分电路连接示意图,下列说法错误的是 ( )
图ZT7-7
A.当小灯泡L两端电压为2.5 V时,它的阻值和定值电阻R的阻值相等
B.图(b)中,当电压U为3 V时,小灯泡L的电阻为5 Ω
C.图(c)中,当电压U为2 V时,干路电流为0.6 A
D.图(c)中,在电压U从0增大到2.5 V的过程中,通过定值电阻R、小灯泡L的电流之差先变大后变小
8.[2020·永州] 如图图ZT7-8甲所示,电源电压恒定不变,R1为定值电阻,R2为滑动变阻器。闭合开关S,将滑片P从最右端逐步移到最左端,记录电流表、电压表的示数,并根据记录的数据作出R1和R2的U-I关系图像如图图乙所示。则下列说法正确的是 ( )
图ZT7-8
A.图Ⅱ为R2的U-I关系图像
B.当R2=R1时,电流的大小为0.2 A
C.电源电压为8 V
D.R1的阻值为30 Ω
9.有一种由酒精气体传感器制成的呼气酒精测试仪被广泛用来检测酒驾,传感器R1的阻值随酒精气体浓度的变化如图图ZT7-9甲所示,工作电路如图图乙所示,电源电压恒为12 V,定值电阻R2=30 Ω。求:
(1)被检测者未喝酒时,R1的阻值。
(2)被检测者酒精气体浓度为0.8 mg/mL时,电流表的示数。
(3)现在公认的酒驾标准为0.2 mg/mL≤酒精气体浓度≤0.8 mg/mL,当电压表示数为4.8 V时,通过计算说明被检测司机是否属于酒驾。
图ZT7-9
答案
1.A
2.S1、S2 4∶1 要使电阻R2、R3并联,则电阻R2、R3中必须有电流通过,所以应闭合开关S1、S2,此时电流表测干路电流,因并联电路中总电阻的倒数等于各分电阻倒数之和,所以,电路中的总电阻:
R===5 Ω,
此时电流表的示数:I1== Ω;
断开开关S1、S2时,R1、R2串联,电流表测电路中的电流,因串联电路中总电阻等于各分电阻之和,所以,此时电流表的示数:I2===,
所以,I1∶I2=∶=4∶1。
3.(1)当开关S1、S2断开时,电阻R2与R3串联,电流表的示数:I1===1.2 A;电压表的示数:U1=I1R2=1.2 A×6 Ω=7.2 V。
(2)当开关S1、S2均闭合时,电阻R1与R2并联,电压表的示数为电源电压,为12 V;
电路总电阻:R===2.4 Ω,
电流表的示数:I===5 A。
4.(1)短路
(2)开关S闭合、S1断开时,电路为R1的简单电路,由欧姆定律知,电流表示数:I===0.4 A。
(3)开关S、S1都闭合时,电流表测干路电流,通过R1的电流为0.4 A不变,故通过变阻器的最大电流为I2=I最大-I=0.6 A-0.4 A=0.2 A,由欧姆定律可得,变阻器R2连入电路的最小阻值:R2===30 Ω。
5.由图甲知,R1与R2串联,电压表测R2两端的电压,电流表测电路中的电流。当滑片P在a端时,只有R1连入电路中,此时电路中电流最大,由图乙知,I1=0.6 A,由欧姆定律可得,电源电压:U=I1R1=0.6 A×R1①;当滑片P在b端时,R2(接入电路的电阻最大)与R1串联,电路中电流最小,由图乙知,I2=0.2 A,电压表示数为:UV=2 V,根据串联电路的规律及欧姆定律可得,电源电压:U=I2R1+UV=0.2 A×R1+2 V②,由①②得:R1=5 Ω,代入①得:电源电压:U=3 V。
6.(1)当滑动变阻器R3的滑片P移到最左端,闭合开关S1、S2时,电阻R1、R2并联,电压表测量电源电压,即电源电压为3 V,电流表测量干路电流;因为并联电路各支路两端电压相等且等于电源电压,所以U1=U2=U=3 V,通过R2的电流为I2===0.3 A,根据并联电路干路电流等于各支路电流之和知,通过R1的电流为I1=I-I2=0.5 A-0.3 A=0.2 A,R1的阻值为R1===15 Ω。
(2)只闭合开关S1,滑动变阻器R3的滑片P移到最右端时,R1与R3(接入电路的电阻最大)串联,电压表测R1两端的电压,此时电路中的电流为I'=== A,R1两端的电压为U1'=I'R1= A×15 Ω=1 V,即电压表的示数为1 V。
(3)只闭合开关S2时,R2与R3串联,当滑动变阻器接入电路的电阻为0时,电路中电流最大,最大电流为I最大===0.3 A。
7.B 由图(a)可知,当R、L两端电压均为2.5 V时,通过两者的电流均为0.5 A,则由I=的变形式R=可知,R、L的阻值相等,故A正确;图(b)中,R与L串联,由图(a)可知,当电路中的电流I=0.2 A、UR=1 V、UL=2 V时,电压U为3 V,此时L的电阻RL===10 Ω,故B错误;图(c)中,R与L并联,由图(a)可知,当电压U=2 V、IR=0.4 A、IL=0.2 A时,干路电流为0.6 A,故C正确;图(c)中,R与L并联,由图(a)可知,在电压U从0增大到2.5 V的过程中,通过R、L的电流之差先变大后变小,故D正确。
8.C 由图甲知,R1与R2串联,电压表V1测R1两端的电压,电压表V2测R2两端的电压,滑片在最左端时,R2接入电路的阻值为零,此时电压表V2示数为零,由图像可得,图线I反映电压表V2示数(即R2两端的电压)随电流的变化,则图线Ⅱ为R1的U-I关系图像,故A错误;串联电路中各处的电流相等,当R2=R1时,由U=IR可知,两电阻两端的电压相同,由图乙知,即为两图线的交点,可知电流为0.4 A,B错误;由图乙知,当电流为0.4 A时,两电压表示数均为4 V,则电源电压U=4 V+4 V=8 V,C正确;当滑片移动到最左端时,电路中只有R1,电压表V2示数为0,电路中电流为0.8 A,由欧姆定律可得,R1===10 Ω,D错误。
9.(1)由图甲可知,当被检测者未喝酒时,即酒精气体浓度为0时,R1的电阻为60 Ω。
(2)由图甲可知,当酒精气体浓度为0.8 mg/mL时,R1的电阻为10 Ω,
则R总=R1'+R2=10 Ω+30 Ω=40 Ω,
此时电路中电流:I===0.3 A,
即电流表的示数为0.3 A。
(3)当电压表的示数U1=4.8 V时,
则U2=U-U1=12 V-4.8 V=7.2 V,
电路中的电流:I1=I2===0.24 A,
此时传感器R1的阻值:R1″===20 Ω。
由图甲可知,被检测者的酒精气体浓度为0.3 mg/mL,因0.2 mg/mL<0.3 mg/mL<0.8 mg/mL,所以被检测者属于酒驾。
同课章节目录
- 第十二章 温度与物态变化
- 第一节 温度与温度计
- 第二节 熔化与凝固
- 第三节 汽化与液化
- 第四节 升华与凝华
- 第五节 全球变暖与水资源危机
- 第十三章 内能与热机
- 第一节 物体的内能
- 第二节 科学探究:物质的比热容
- 第三节 内燃机
- 第四节 热机效率和环境保护
- 第十四章 了解电路
- 第一节 电是什么
- 第二节 让电灯发光
- 第三节 连接串联电路和并联电路
- 第四节 科学探究:串联和并联电路的电流
- 第五节 测量电压
- 第十五章 探究电路
- 第一节 电阻和变阻器
- 第二节 科学探究:欧姆定律
- 第三节 “伏安法”测电阻
- 第四节 电阻的串联和并联
- 第五节 家庭用电
- 第十六章 电流做功与电功率
- 第一节 电流做功
- 第二节 电流做功的快慢
- 第三节 测量电功率
- 第四节 科学探究:电流的热效应
- 第十七章 从指南针到磁浮列车
- 第一节 磁是什么
- 第二节 电流的磁场
- 第三节 科学探究:电动机为什么会转动
- 第十八章 电能从哪里来
- 第一节 电能的产生
- 第二节 科学探究:怎样产生感应电流
- 第三节 电能的输送
- 第十九章 走进信息时代
- 第一节 感受信息
- 第二节 让信息“飞”起来
- 第三节 踏上信息高速公路
- 第二十章 能源、材料与社会
- 第一节 能量的转化与守恒
- 第二节 能源的开发和利用
- 第三节 材料的开发和利用
