人教版八年级上册11.1.1三角形的边课件(共20张PPT)
文档属性
| 名称 | 人教版八年级上册11.1.1三角形的边课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-26 21:17:05 | ||
图片预览





文档简介
(共20张PPT)
11.1.1 三角形的边
第十一章 三角形
2022-2023学年初中数学人教版八年级上册
学习目标
1.理解三角形的定义,认识三角形的边、角、顶点;
能用符号语言表示三角形,能识别不同形状的三角形;
掌握三角形的三边关系,并能用它解决相关问题。
2.在将三角形分类的过程中,进一步体会分类的原则;
在解决问题的过程中,理解分类讨论的数学思想。
3.学会用数学的眼光观察生活,感受生活中蕴含的数学之美。
学习目标
重点:能用符号语言表示三角形,能从图中识别三角形;
教学重难点
难点:理解三角形三边间的不等关系。
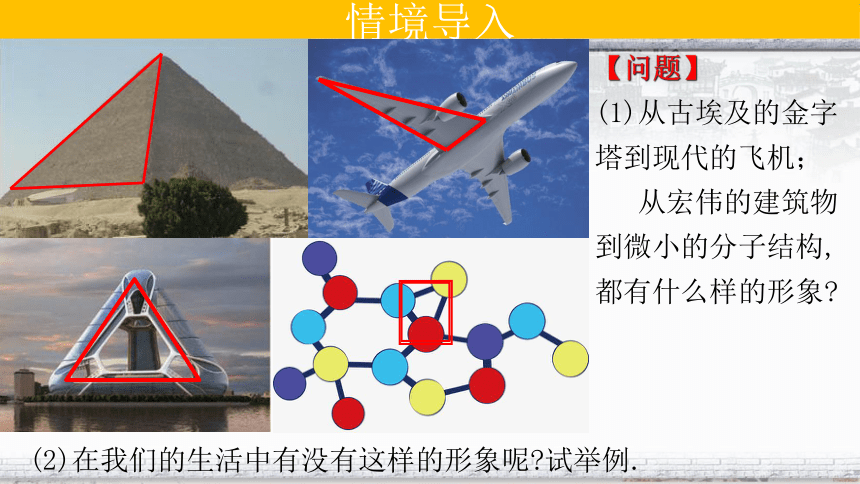
情境导入
【问题】
(1)从古埃及的金字塔到现代的飞机;
从宏伟的建筑物到微小的分子结构,都有什么样的形象
(2)在我们的生活中有没有这样的形象呢 试举例.
探究1:
下列哪些是三角形?
( 1 )
( 2 )
( 3 )
( 4 )
( 5 )
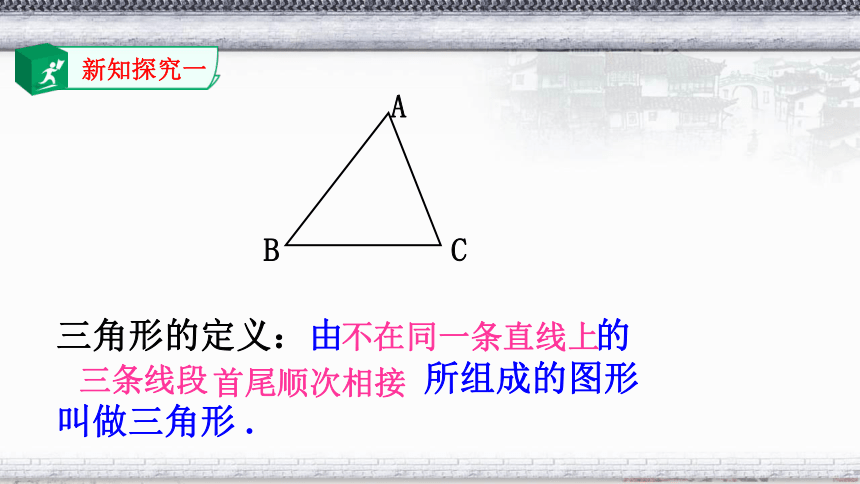
新知探究一
观察三角形,他是如何构成的?你能描述一下三角形吗?
三角形的定义:由 的
所组成的图形
叫做三角形 .
不在同一条直线上
三条线段
首尾顺次相接
A
B
C
新知探究一
认识三角形
1. 三角形的顶点:
分别是点A、点B、点C.
2. 三角形的边:
分别是线段AB、
3. 三角形的内角(简称角):
分别是∠A、∠B、∠C.
A
B
C
线段BC、
线段CA.
新知探究一
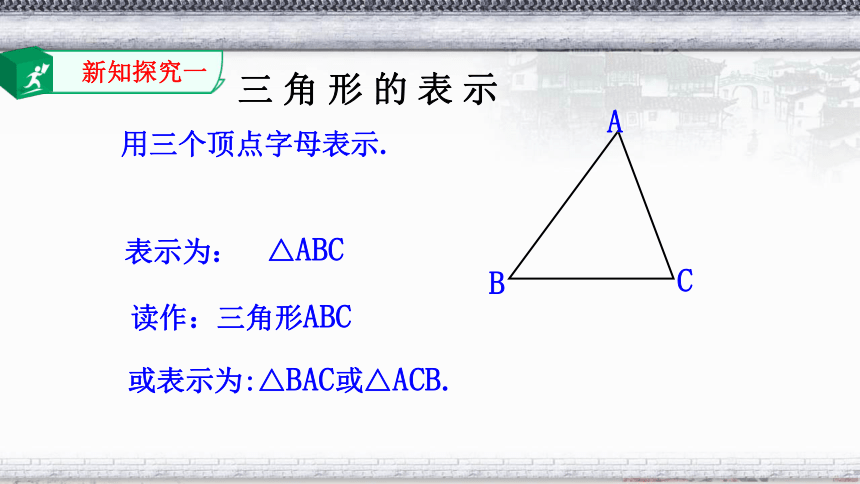
新知探究一
三 角 形 的 表 示
A
B
C
表示为:
用三个顶点字母表示.
或表示为:△BAC或△ACB.
△ABC
读作:三角形ABC
新知探究一
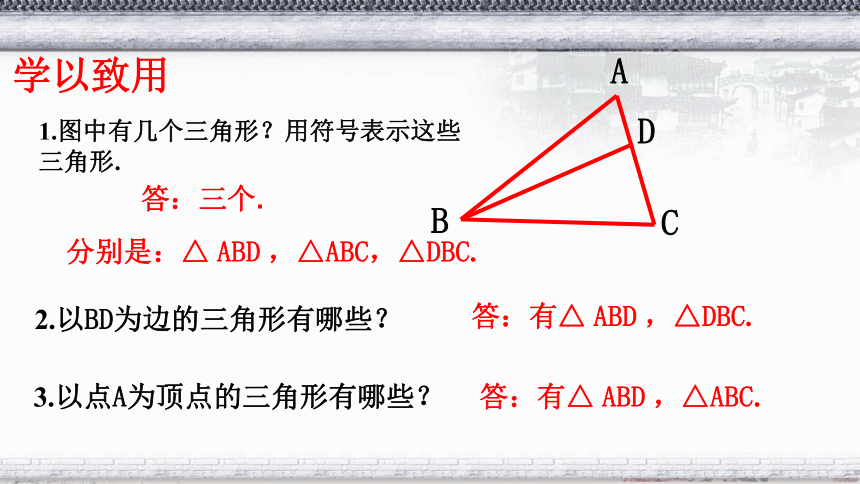
新知探究一
D
B
A
C
1.图中有几个三角形?用符号表示这些三角形.
2.以BD为边的三角形有哪些?
3.以点A为顶点的三角形有哪些?
答:有△ ABD ,△DBC.
分别是:△ ABD ,△ABC,△DBC.
答:有△ ABD ,△ABC.
学以致用
答:三个.
新知探究二
这是同学们画的三角形,你能将这些三角形分类吗?
三角形
直角三角形
锐角三角形
钝角三角形
三角形按角分类
新知探究二
三角形
三边都不相等的三角形
等腰三角形
底边和腰不相等的等腰三角形
等边三角形
三角形按边分类
新知探究二
学以致用
判断下列说法是否正确:
(2)三角形按边分为三类:分别是等腰三角形、等边三角形和不等边三角形.
(1)三角形按边分为两类:分别是等腰三角形和等边三角形.
( )
( )
探究3:小黄人要从B点去C点觅食,请你帮忙选择最佳的路径.
新知探究三
小黄人从点B到点C有两条路,哪条路近?
为什么?你能得到一个怎样的不等式?
小黄人从点A到点C呢?
从点B到点A呢?
b+c>a
c+a>b
a+b>c
a-c<b
a-b<c
b-c<a
两边之和大于第三边
两边之差小于第三边。
做一做!
有三根木棒长分别为3 cm,6 cm,2 cm,它们能否围成三角形?为什么?
你有什么更好的办法吗?
用两条小边之和与大边比较.
用最大边减中边的差与最小边比较.
2.下列长度的三条线段能否组成三角形?为什么?
(1) 3,8,4 ( )
(2) 6,5 ,2 ( )
(3) 5,6,10 ( )
(4) 2,8 ,5 ( )
不能
能
能
不能
课堂练习
【例】用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,那么各边的长是多少?
(2)能围成有一边的长是4cm的等腰三角形吗?为什么 ?
解:(1)设底边长为xcm,则腰长为2xcm,x+2x+2x=18.
综上所述,可以围成底边长是4cm的等腰三角形.
(2)①若底边长为4cm,设腰长为xcm,则有4+2x=18.解得:x=7.
②若腰长为4cm,设底边长为xcm,则有2×4+x=18.解得:x=10.
∵4+4<10,不符合三角形两边的和大于第三边,
∴不能围成腰长是4cm的等腰三角形.
解得:x=3.6.所以三边长分别为3.6cm,7.2cm,7.2cm.
能力提升:
在△ABC中,若 a =3,b =7,则第三边 c 的取值范围是 .
既要考虑“两边的和大于第三边”,又要考虑“两边的差小于第三边”.
a - b < c < a + b
在△ABC中,若a =3,b=7,则其周长 l 的取值范围是 .
4 < c < 10
14 < l < 20
三角形
定义
表示方
分类法
三边关
系定理
按边分类
按角分类
a - b < c < a + b
小 结
课堂小结
谢谢聆听
11.1.1 三角形的边
第十一章 三角形
2022-2023学年初中数学人教版八年级上册
学习目标
1.理解三角形的定义,认识三角形的边、角、顶点;
能用符号语言表示三角形,能识别不同形状的三角形;
掌握三角形的三边关系,并能用它解决相关问题。
2.在将三角形分类的过程中,进一步体会分类的原则;
在解决问题的过程中,理解分类讨论的数学思想。
3.学会用数学的眼光观察生活,感受生活中蕴含的数学之美。
学习目标
重点:能用符号语言表示三角形,能从图中识别三角形;
教学重难点
难点:理解三角形三边间的不等关系。
情境导入
【问题】
(1)从古埃及的金字塔到现代的飞机;
从宏伟的建筑物到微小的分子结构,都有什么样的形象
(2)在我们的生活中有没有这样的形象呢 试举例.
探究1:
下列哪些是三角形?
( 1 )
( 2 )
( 3 )
( 4 )
( 5 )
新知探究一
观察三角形,他是如何构成的?你能描述一下三角形吗?
三角形的定义:由 的
所组成的图形
叫做三角形 .
不在同一条直线上
三条线段
首尾顺次相接
A
B
C
新知探究一
认识三角形
1. 三角形的顶点:
分别是点A、点B、点C.
2. 三角形的边:
分别是线段AB、
3. 三角形的内角(简称角):
分别是∠A、∠B、∠C.
A
B
C
线段BC、
线段CA.
新知探究一
新知探究一
三 角 形 的 表 示
A
B
C
表示为:
用三个顶点字母表示.
或表示为:△BAC或△ACB.
△ABC
读作:三角形ABC
新知探究一
新知探究一
D
B
A
C
1.图中有几个三角形?用符号表示这些三角形.
2.以BD为边的三角形有哪些?
3.以点A为顶点的三角形有哪些?
答:有△ ABD ,△DBC.
分别是:△ ABD ,△ABC,△DBC.
答:有△ ABD ,△ABC.
学以致用
答:三个.
新知探究二
这是同学们画的三角形,你能将这些三角形分类吗?
三角形
直角三角形
锐角三角形
钝角三角形
三角形按角分类
新知探究二
三角形
三边都不相等的三角形
等腰三角形
底边和腰不相等的等腰三角形
等边三角形
三角形按边分类
新知探究二
学以致用
判断下列说法是否正确:
(2)三角形按边分为三类:分别是等腰三角形、等边三角形和不等边三角形.
(1)三角形按边分为两类:分别是等腰三角形和等边三角形.
( )
( )
探究3:小黄人要从B点去C点觅食,请你帮忙选择最佳的路径.
新知探究三
小黄人从点B到点C有两条路,哪条路近?
为什么?你能得到一个怎样的不等式?
小黄人从点A到点C呢?
从点B到点A呢?
b+c>a
c+a>b
a+b>c
a-c<b
a-b<c
b-c<a
两边之和大于第三边
两边之差小于第三边。
做一做!
有三根木棒长分别为3 cm,6 cm,2 cm,它们能否围成三角形?为什么?
你有什么更好的办法吗?
用两条小边之和与大边比较.
用最大边减中边的差与最小边比较.
2.下列长度的三条线段能否组成三角形?为什么?
(1) 3,8,4 ( )
(2) 6,5 ,2 ( )
(3) 5,6,10 ( )
(4) 2,8 ,5 ( )
不能
能
能
不能
课堂练习
【例】用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,那么各边的长是多少?
(2)能围成有一边的长是4cm的等腰三角形吗?为什么 ?
解:(1)设底边长为xcm,则腰长为2xcm,x+2x+2x=18.
综上所述,可以围成底边长是4cm的等腰三角形.
(2)①若底边长为4cm,设腰长为xcm,则有4+2x=18.解得:x=7.
②若腰长为4cm,设底边长为xcm,则有2×4+x=18.解得:x=10.
∵4+4<10,不符合三角形两边的和大于第三边,
∴不能围成腰长是4cm的等腰三角形.
解得:x=3.6.所以三边长分别为3.6cm,7.2cm,7.2cm.
能力提升:
在△ABC中,若 a =3,b =7,则第三边 c 的取值范围是 .
既要考虑“两边的和大于第三边”,又要考虑“两边的差小于第三边”.
a - b < c < a + b
在△ABC中,若a =3,b=7,则其周长 l 的取值范围是 .
4 < c < 10
14 < l < 20
三角形
定义
表示方
分类法
三边关
系定理
按边分类
按角分类
a - b < c < a + b
小 结
课堂小结
谢谢聆听
