人教版八年级上册 11.1.2三角形的高、中线与角平分线课件(共34张PPT)
文档属性
| 名称 | 人教版八年级上册 11.1.2三角形的高、中线与角平分线课件(共34张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-26 21:30:51 | ||
图片预览




文档简介
(共34张PPT)
11.1.2三角形的高、中线与角平分线
怎样等分三角糕?
学习目标
1.理解三角形的高、中线与角平分线等概念;
2.会用工具画三角形的高、中线与角平分线;
3.会用几何语言表达三角形的高、中线与角平分线的定义;
4.运用概念及性质解决简单问题.
11.1.2 三角形的高、中线与角平分线
1.三角形的高、中线、角平分线及重心是怎样定义的?
注意:①把定义中的关键词画出来;
②试用几何语言表述前三个定义.
2.怎样画三角形的高、中线、角平分线?
自学课本第4-5页的内容,完成下列问题:
自学指导
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
A
D
C
B
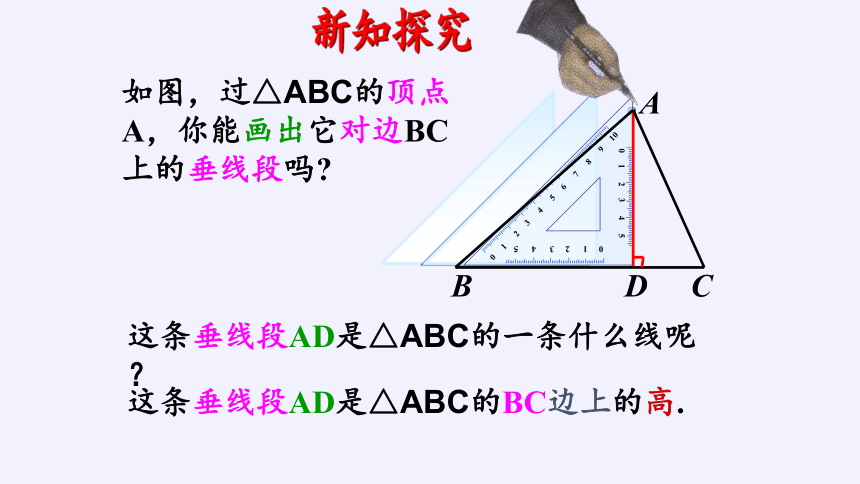
如图,过△ABC的顶点A,你能画出它对边BC上的垂线段吗
这条垂线段AD是△ABC的一条什么线呢?
这条垂线段AD是△ABC的BC边上的高.
新知探究
A
D
C
B
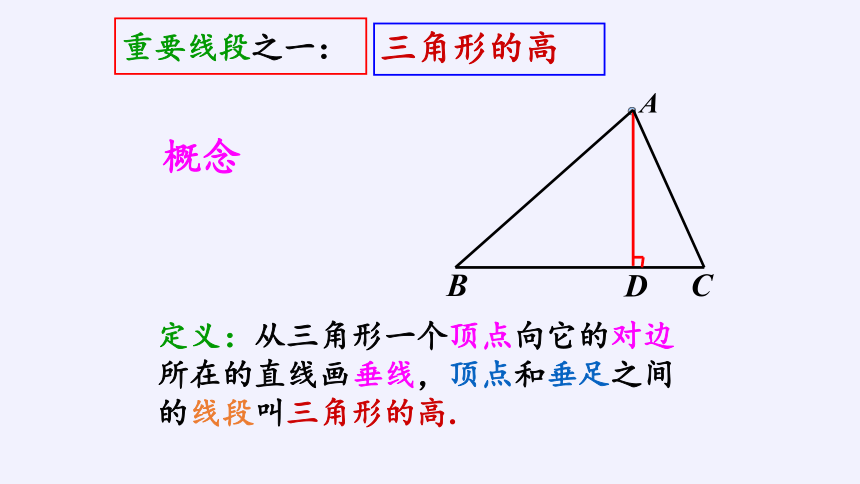
定义:从三角形一个顶点向它的对边
所在的直线画垂线,顶点和垂足之间的线段叫三角形的高.
重要线段之一:
三角形的高
概念
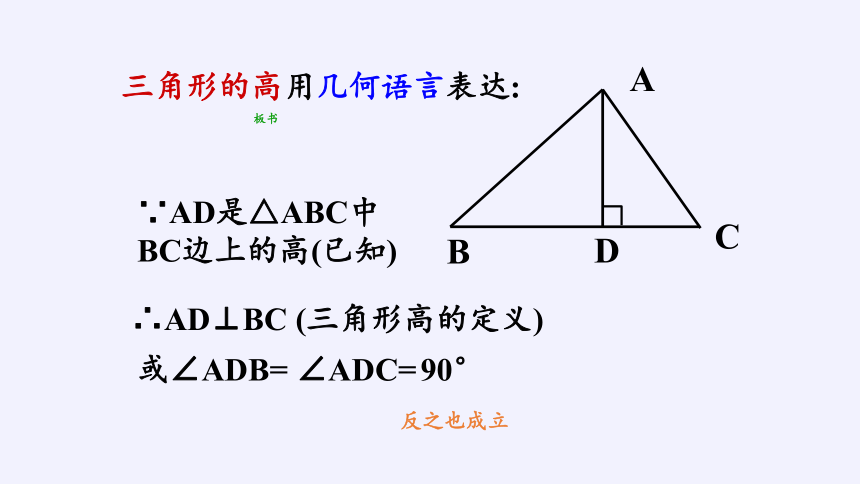
三角形的高用几何语言表达:
B
C
A
D
∵AD是△ABC中
BC边上的高(已知)
∴AD⊥BC (三角形高的定义)
或∠ADB= ∠ADC= 90°
反之也成立
板书
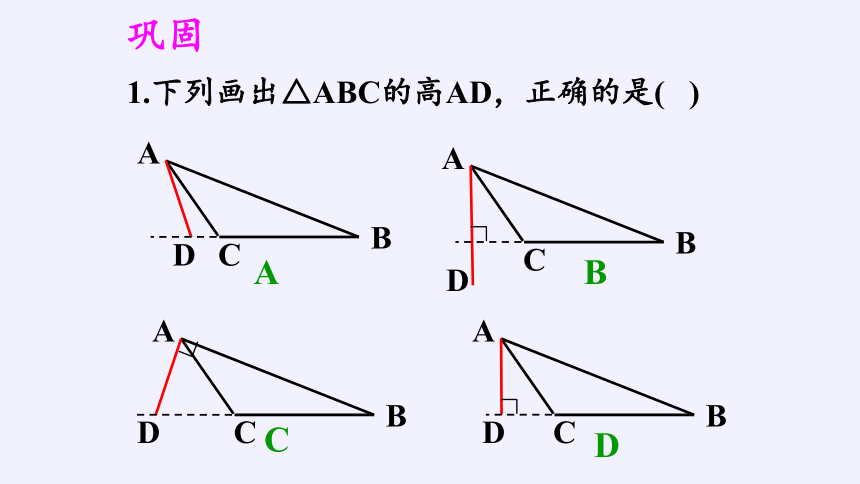
1.下列画出△ABC的高AD,正确的是( )
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
A
B
C
D
巩固
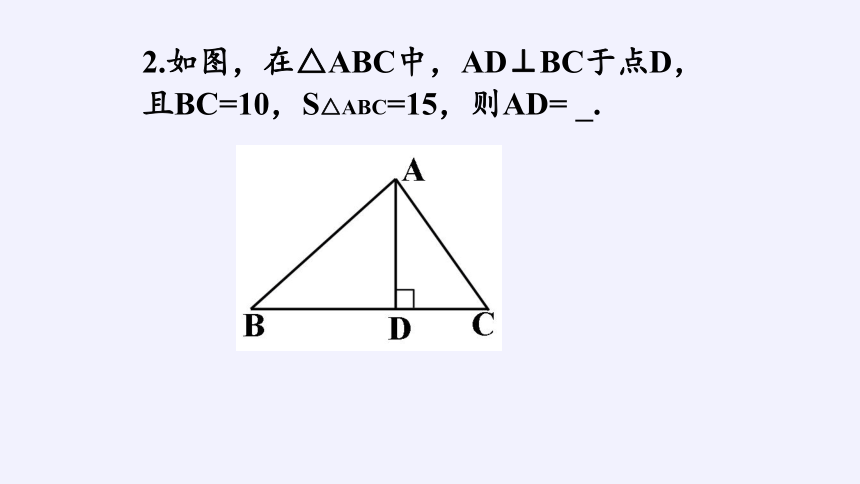
2.如图,在△ABC中,AD⊥BC于点D,且BC=10,S△ABC=15,则AD= .
A
C
B
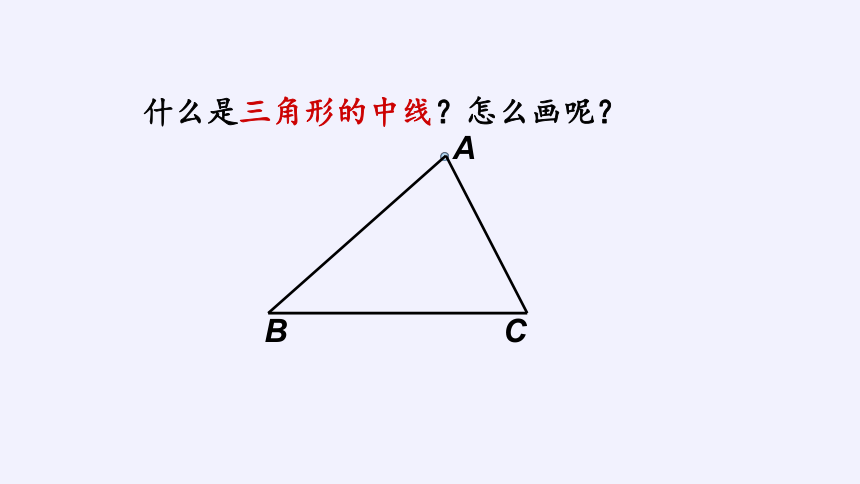
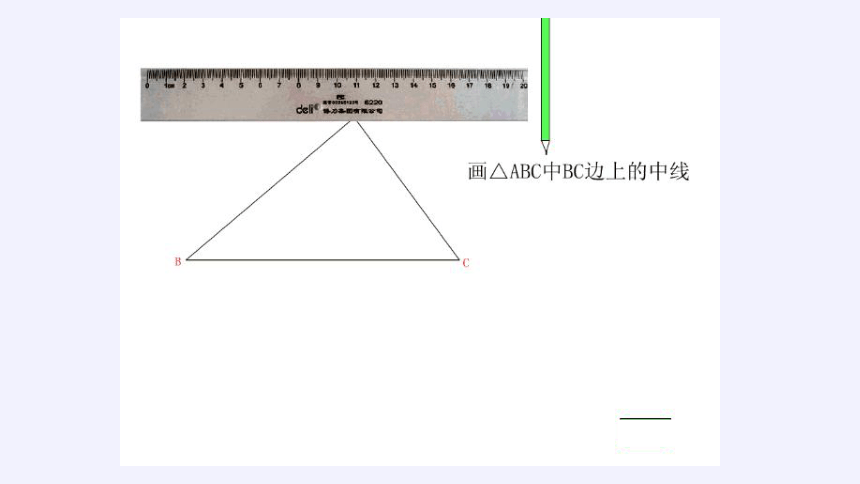
什么是三角形的中线?怎么画呢?
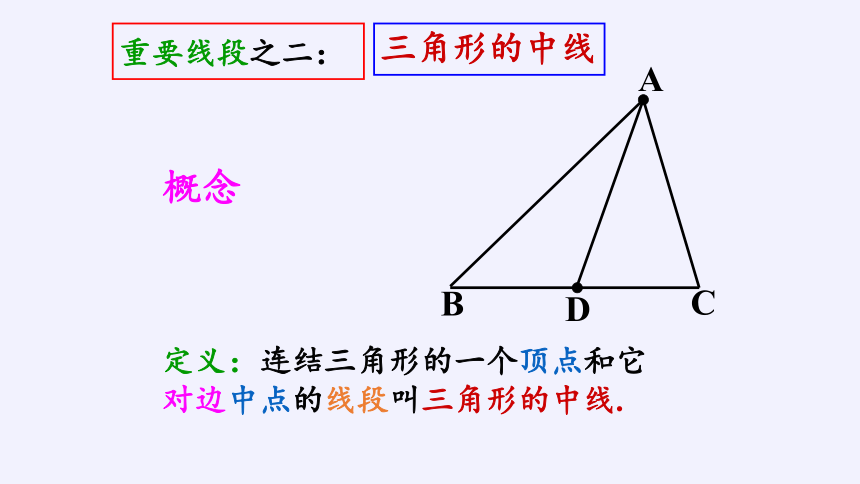
三角形的中线
B
C
D
A
定义:连结三角形的一个顶点和它
对边中点的线段叫三角形的中线.
重要线段之二:
概念
三角形的中线用几何语言表达:
B
C
D
A
∵AD是△ABC中
BC边上的中线(已知)
∴BD=CD= BC (三角形中线的定义)
或BC=2BD=2CD
反之也成立
请类比高的表达方法进行
类比思想
板书
B
C
D
A
讨论:AD是△ABC中BC边上的中线,则S△ADB=S△ADC成立吗?它们与S△ABC的大小关系呢 为什么?
E
结论:三角形的一条中线,把原三角形分成了面积相等的两个三角形.
等分三角糕的“这一刀”你会用数学语言描述了吗?
数学源于生活又服务于生活
等积思想
1. 如图,在△ABC中,点D是AB边上的中点,且AD=7,则,AB= .
巩固
2.如图,在△ABC中,点D、E分别是AB、AC边上的中点,且S△ABC=20,则S△AED= .
A
C
B
什么是三角形的角平分线?怎么画呢?
三角形的角平分线
B
C
D
A
定义:三角形一个内角的平分线与它
的对边相交,这个角的顶点与交点之间的线段叫三角形的角平分线.
︶
︶
1
2
重要线段之三:
概念
三角形的角平分线
用几何语言表示
B
C
D
A
∵AD是△ABC中
∠BAC的平分线(已知)
∴∠BAD=∠CAD = ∠BAC
(三角形角平分线的定义)
或∠BAC=2∠BAD=2∠CAD
反之也成立
板书
︶
︶
1
2
如图,在△ABC中,∠1= ∠2 =300,则∠ACB= .
巩固
折叠
一个三角形有几条高?几条中线?几条角平分线?
三角板
量角器
刻度尺
高
中线
角平分线
你会折叠出三角形的高、中线和角平分线吗?
直角三角形
钝角三角形
锐角三角形
画出不同类型的三角形的
三条高、三条中线、三条角平分线.
探究
观察所画线段有什么位置关系?
A
B
C
D
E
F
B
D
E
F
A
C
探究
画出三角形三边上的高
A
B
C
D
●
你有什么发现?
三角形的三条高所在直线交于一点
●
探究
画出三角形三边上的中线
你有什么发现?
什么是三角形的重心?
三角形的三条中线在三角形的内部交于一点.
探究
画出三角形三个内角角的平分线
你有什么发现?
三角形的三条角平分线在三角形的内部交于一点.
三角形的角平分线与角的平分线有什么区别?
小结
三角形的重要线段
三角形的高
三角形的中线
三角形的角平分线
垂直
90°的角
线段有关
面积有关
角有关
当堂检测
1.如图,在△ABC中,AD是角平分线,DE//AC,DF//AB.试判断∠3和∠4的关系,并说明理由.
2.线段BM是△ABC的中线,若AB=5cm,BC=13cm,那么△BCM的周长与△ABM的周长之差是多少cm?
3. 在△ABC中,∠ACB=90°,CB=6, CA=8, AB=10,则AB边上的高CD是多少?
某种植户有一块三角形的地,如图△ABC,他想分成面积相等的四个三角形,来种植四种不同的农作物,请你帮他设计出分割方案(至少四种).
拓展延伸
课堂反思
谈谈你的收获……
明白四个概念:
会画三种线段:
体会两种思想:
掌握一种语言:
三角形的高、中线、角平分线、重心
三角形的高、中线、角平分线
几何语言
一个三角形的“三线”交于一点
说说你的困惑?
了解一个事实:
类比思想、等积思想
课后作业
1. 课本第8-9页习题,3、4、8、9;
2. 预习课本第6-7页的内容.
谢 谢
11.1.2三角形的高、中线与角平分线
怎样等分三角糕?
学习目标
1.理解三角形的高、中线与角平分线等概念;
2.会用工具画三角形的高、中线与角平分线;
3.会用几何语言表达三角形的高、中线与角平分线的定义;
4.运用概念及性质解决简单问题.
11.1.2 三角形的高、中线与角平分线
1.三角形的高、中线、角平分线及重心是怎样定义的?
注意:①把定义中的关键词画出来;
②试用几何语言表述前三个定义.
2.怎样画三角形的高、中线、角平分线?
自学课本第4-5页的内容,完成下列问题:
自学指导
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
A
D
C
B
如图,过△ABC的顶点A,你能画出它对边BC上的垂线段吗
这条垂线段AD是△ABC的一条什么线呢?
这条垂线段AD是△ABC的BC边上的高.
新知探究
A
D
C
B
定义:从三角形一个顶点向它的对边
所在的直线画垂线,顶点和垂足之间的线段叫三角形的高.
重要线段之一:
三角形的高
概念
三角形的高用几何语言表达:
B
C
A
D
∵AD是△ABC中
BC边上的高(已知)
∴AD⊥BC (三角形高的定义)
或∠ADB= ∠ADC= 90°
反之也成立
板书
1.下列画出△ABC的高AD,正确的是( )
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
A
B
C
D
巩固
2.如图,在△ABC中,AD⊥BC于点D,且BC=10,S△ABC=15,则AD= .
A
C
B
什么是三角形的中线?怎么画呢?
三角形的中线
B
C
D
A
定义:连结三角形的一个顶点和它
对边中点的线段叫三角形的中线.
重要线段之二:
概念
三角形的中线用几何语言表达:
B
C
D
A
∵AD是△ABC中
BC边上的中线(已知)
∴BD=CD= BC (三角形中线的定义)
或BC=2BD=2CD
反之也成立
请类比高的表达方法进行
类比思想
板书
B
C
D
A
讨论:AD是△ABC中BC边上的中线,则S△ADB=S△ADC成立吗?它们与S△ABC的大小关系呢 为什么?
E
结论:三角形的一条中线,把原三角形分成了面积相等的两个三角形.
等分三角糕的“这一刀”你会用数学语言描述了吗?
数学源于生活又服务于生活
等积思想
1. 如图,在△ABC中,点D是AB边上的中点,且AD=7,则,AB= .
巩固
2.如图,在△ABC中,点D、E分别是AB、AC边上的中点,且S△ABC=20,则S△AED= .
A
C
B
什么是三角形的角平分线?怎么画呢?
三角形的角平分线
B
C
D
A
定义:三角形一个内角的平分线与它
的对边相交,这个角的顶点与交点之间的线段叫三角形的角平分线.
︶
︶
1
2
重要线段之三:
概念
三角形的角平分线
用几何语言表示
B
C
D
A
∵AD是△ABC中
∠BAC的平分线(已知)
∴∠BAD=∠CAD = ∠BAC
(三角形角平分线的定义)
或∠BAC=2∠BAD=2∠CAD
反之也成立
板书
︶
︶
1
2
如图,在△ABC中,∠1= ∠2 =300,则∠ACB= .
巩固
折叠
一个三角形有几条高?几条中线?几条角平分线?
三角板
量角器
刻度尺
高
中线
角平分线
你会折叠出三角形的高、中线和角平分线吗?
直角三角形
钝角三角形
锐角三角形
画出不同类型的三角形的
三条高、三条中线、三条角平分线.
探究
观察所画线段有什么位置关系?
A
B
C
D
E
F
B
D
E
F
A
C
探究
画出三角形三边上的高
A
B
C
D
●
你有什么发现?
三角形的三条高所在直线交于一点
●
探究
画出三角形三边上的中线
你有什么发现?
什么是三角形的重心?
三角形的三条中线在三角形的内部交于一点.
探究
画出三角形三个内角角的平分线
你有什么发现?
三角形的三条角平分线在三角形的内部交于一点.
三角形的角平分线与角的平分线有什么区别?
小结
三角形的重要线段
三角形的高
三角形的中线
三角形的角平分线
垂直
90°的角
线段有关
面积有关
角有关
当堂检测
1.如图,在△ABC中,AD是角平分线,DE//AC,DF//AB.试判断∠3和∠4的关系,并说明理由.
2.线段BM是△ABC的中线,若AB=5cm,BC=13cm,那么△BCM的周长与△ABM的周长之差是多少cm?
3. 在△ABC中,∠ACB=90°,CB=6, CA=8, AB=10,则AB边上的高CD是多少?
某种植户有一块三角形的地,如图△ABC,他想分成面积相等的四个三角形,来种植四种不同的农作物,请你帮他设计出分割方案(至少四种).
拓展延伸
课堂反思
谈谈你的收获……
明白四个概念:
会画三种线段:
体会两种思想:
掌握一种语言:
三角形的高、中线、角平分线、重心
三角形的高、中线、角平分线
几何语言
一个三角形的“三线”交于一点
说说你的困惑?
了解一个事实:
类比思想、等积思想
课后作业
1. 课本第8-9页习题,3、4、8、9;
2. 预习课本第6-7页的内容.
谢 谢
