人教版八年级上册11.2.1 三角形内角课件(共20张PPT)
文档属性
| 名称 | 人教版八年级上册11.2.1 三角形内角课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-26 21:36:29 | ||
图片预览






文档简介
(共20张PPT)
三角形内角和
(1)知识与技能:
探索三角形的内角和,并初步体会辅助线在解决几何演绎证明中的作用。
(2)过程与方法:
通过“动手—归纳—猜想—证明—解决—收获” 感受数学思考过程的条理性,培养学生的动手实践、大胆猜想、逻辑推理等能力。
(3)情感、态度与价值观:
通过动手、归纳、推断得到数学猜想,体验数学充满探索性、创造性,使学生乐于学数学,在数学活动中获得成功的体验,增强自信心。
教学目标
重、难点
重点:探索和证明三角形内角和定理;
难点:三角形内角和定理的证明
想一想:
假如你正站在金字塔下,现有用于测量角的量角器,但为了保护文化遗产,在不允许人攀爬的情况下,你能否想办法知道塔尖处一个侧面角的度数吗?说一说你的做法。
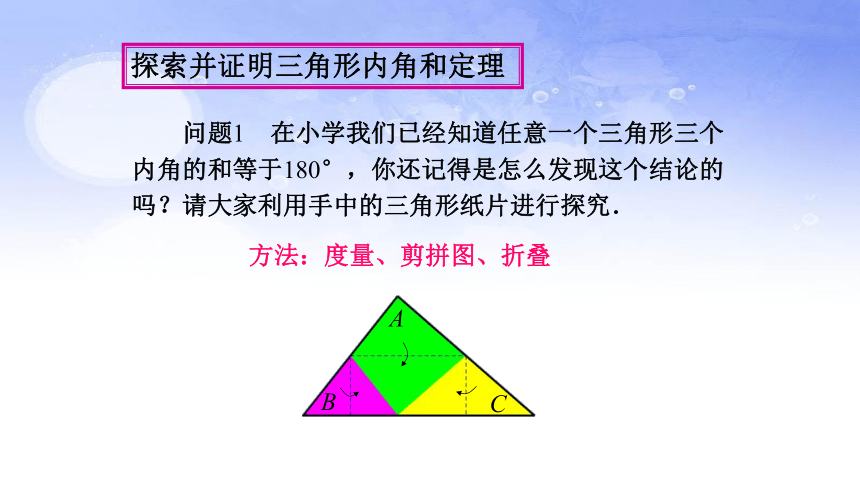
问题1 在小学我们已经知道任意一个三角形三个
内角的和等于180°,你还记得是怎么发现这个结论的
吗?请大家利用手中的三角形纸片进行探究.
探索并证明三角形内角和定理
A
B
C
方法:度量、剪拼图、折叠
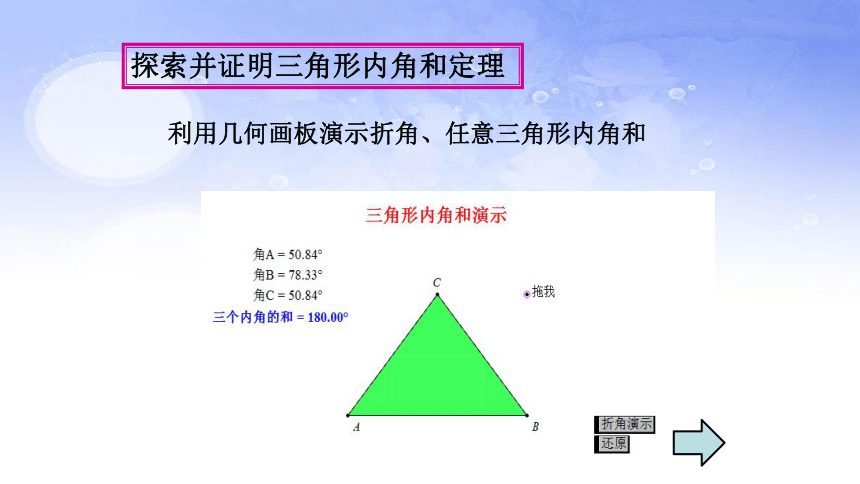
探索并证明三角形内角和定理
利用几何画板演示折角、任意三角形内角和
探索并证明三角形内角和定理
追问1 运用度量的方法,得出的三个内角的和都
是180°吗?为什么会不一样呢?
测量可能会有误差.
追问2 通过剪拼图或折叠的方法验证了手中的三角形纸片的三个内角和等于180°,但我们手中的三角形只是所有三角形中有限的几个,而形状不同的三角形有无数多个,我们如何能得出“所有的三角形的三个内角的和都等于180°”这个结论呢?
需要通过推理的方法去证明.
猜想:
三角形内角和为180°
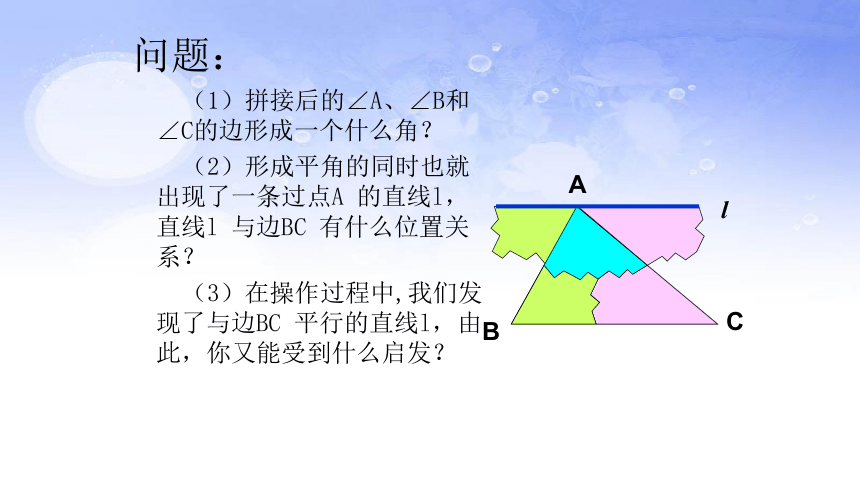
问题:
(1)拼接后的∠A、∠B和∠C的边形成一个什么角?
(2)形成平角的同时也就出现了一条过点A 的直线l,直线l 与边BC 有什么位置关系?
(3)在操作过程中,我们发现了与边BC 平行的直线l,由此,你又能受到什么启发?
A
l
B
C
已知:如图,△ABC
求证:∠A+∠B+∠C=1800
F
E
C
B
A
证明:过点A作EF∥BC,
∵ EF∥BC(已知)
∴∠B=∠BAE
(两直线平行,内错角相等)
∠C=∠CAF
(两直线平行,内错角相等)
又∵∠BAE+∠CAF+∠BAC=180°
∴∠B+∠C+∠BAC=180°
在这里,为了证明的需要,在原来的图形上添加的线叫做辅助线。在平面几何里,辅助线通常画成虚线。
这种方法你会证明吗?小组合作试一试
证明三角形内角和证明
2
1
E
D
C
B
A
开启 智慧
选择其中一种方法证明三角形内角和定理吗?
添加辅助线思路:1、构造平角2、构造同旁内角
A
B
C
E
图1
E
A
B
C
D
F
图2
A
N
B
C
T
S
图3
P
Q
R
M
A
N
B
C
T
S
图4
P
Q
R
M
(
A
B
C
E
D
F
(
(
1
2
3
4
(
图5
猜想:
三角形内角和为180°
定理:
为了证明三个角的和为1800,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.
运用三角形内角和定理
例1:如图,在△ABC 中, ∠BAC =40°, ∠B =
75°,AD 是△ABC 的角平分线.求∠ADB 的度数.
C
B
D
A
解:由∠BAC=40°,AD是△ABC的角平分线
在△ABD中,
∠ADB=1800 - ∠B - ∠BAD
= 1800 -75° -20°
= 85°
得∠BAD= ∠BAC=20°
例2:已知三角形三个内角的度数之比为1:3:5,求这三个内角的度数.
解:设三个内角度数分别为:x、3x、5x,
由三角形内角和为180°得
x+3x+5x=180°
解得 x=20°
所以三个内角度数分别为20°,60°,100°.
1、如图,说出各图中∠1 的度数.
80°
50°
1
30°
105°
1
22°
1
(1)
(2)
(3)
跟踪练习 第一关
(1)在△ABC中,∠A=55°,∠ B=43°
则∠ACB= ,∠ACD=_______.
(2)在△ABC中,∠A=80°,∠B=∠C , 则∠C=____度.
82°
C
B
A
D
98°
50
跟踪练习 第二关
在△ABC中,∠A=80°,∠B=∠C , 求∠C的度数。
A
B
C
跟踪练习 第三关
解:在△ABC中,
∠A+∠B+∠C=180°,
∠A=80°
∴∠B+∠C=100°
∵∠B=∠C
∴∠B=∠C=500
如图,在△ABC中,∠ABC=70°,∠C=65°,BD⊥AC于D,求∠ABD,∠CBD的度数。
A
B
C
D
跟踪练习 第四关
作业:
必做题:教材16页习题11.2第1、2题
选做题:
在△ABC中,AB=AC,∠A=40°,∠ABC的角平分线BD交AC于D,求∠ADB 、∠ DBC的度数。
三角形内角和
(1)知识与技能:
探索三角形的内角和,并初步体会辅助线在解决几何演绎证明中的作用。
(2)过程与方法:
通过“动手—归纳—猜想—证明—解决—收获” 感受数学思考过程的条理性,培养学生的动手实践、大胆猜想、逻辑推理等能力。
(3)情感、态度与价值观:
通过动手、归纳、推断得到数学猜想,体验数学充满探索性、创造性,使学生乐于学数学,在数学活动中获得成功的体验,增强自信心。
教学目标
重、难点
重点:探索和证明三角形内角和定理;
难点:三角形内角和定理的证明
想一想:
假如你正站在金字塔下,现有用于测量角的量角器,但为了保护文化遗产,在不允许人攀爬的情况下,你能否想办法知道塔尖处一个侧面角的度数吗?说一说你的做法。
问题1 在小学我们已经知道任意一个三角形三个
内角的和等于180°,你还记得是怎么发现这个结论的
吗?请大家利用手中的三角形纸片进行探究.
探索并证明三角形内角和定理
A
B
C
方法:度量、剪拼图、折叠
探索并证明三角形内角和定理
利用几何画板演示折角、任意三角形内角和
探索并证明三角形内角和定理
追问1 运用度量的方法,得出的三个内角的和都
是180°吗?为什么会不一样呢?
测量可能会有误差.
追问2 通过剪拼图或折叠的方法验证了手中的三角形纸片的三个内角和等于180°,但我们手中的三角形只是所有三角形中有限的几个,而形状不同的三角形有无数多个,我们如何能得出“所有的三角形的三个内角的和都等于180°”这个结论呢?
需要通过推理的方法去证明.
猜想:
三角形内角和为180°
问题:
(1)拼接后的∠A、∠B和∠C的边形成一个什么角?
(2)形成平角的同时也就出现了一条过点A 的直线l,直线l 与边BC 有什么位置关系?
(3)在操作过程中,我们发现了与边BC 平行的直线l,由此,你又能受到什么启发?
A
l
B
C
已知:如图,△ABC
求证:∠A+∠B+∠C=1800
F
E
C
B
A
证明:过点A作EF∥BC,
∵ EF∥BC(已知)
∴∠B=∠BAE
(两直线平行,内错角相等)
∠C=∠CAF
(两直线平行,内错角相等)
又∵∠BAE+∠CAF+∠BAC=180°
∴∠B+∠C+∠BAC=180°
在这里,为了证明的需要,在原来的图形上添加的线叫做辅助线。在平面几何里,辅助线通常画成虚线。
这种方法你会证明吗?小组合作试一试
证明三角形内角和证明
2
1
E
D
C
B
A
开启 智慧
选择其中一种方法证明三角形内角和定理吗?
添加辅助线思路:1、构造平角2、构造同旁内角
A
B
C
E
图1
E
A
B
C
D
F
图2
A
N
B
C
T
S
图3
P
Q
R
M
A
N
B
C
T
S
图4
P
Q
R
M
(
A
B
C
E
D
F
(
(
1
2
3
4
(
图5
猜想:
三角形内角和为180°
定理:
为了证明三个角的和为1800,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.
运用三角形内角和定理
例1:如图,在△ABC 中, ∠BAC =40°, ∠B =
75°,AD 是△ABC 的角平分线.求∠ADB 的度数.
C
B
D
A
解:由∠BAC=40°,AD是△ABC的角平分线
在△ABD中,
∠ADB=1800 - ∠B - ∠BAD
= 1800 -75° -20°
= 85°
得∠BAD= ∠BAC=20°
例2:已知三角形三个内角的度数之比为1:3:5,求这三个内角的度数.
解:设三个内角度数分别为:x、3x、5x,
由三角形内角和为180°得
x+3x+5x=180°
解得 x=20°
所以三个内角度数分别为20°,60°,100°.
1、如图,说出各图中∠1 的度数.
80°
50°
1
30°
105°
1
22°
1
(1)
(2)
(3)
跟踪练习 第一关
(1)在△ABC中,∠A=55°,∠ B=43°
则∠ACB= ,∠ACD=_______.
(2)在△ABC中,∠A=80°,∠B=∠C , 则∠C=____度.
82°
C
B
A
D
98°
50
跟踪练习 第二关
在△ABC中,∠A=80°,∠B=∠C , 求∠C的度数。
A
B
C
跟踪练习 第三关
解:在△ABC中,
∠A+∠B+∠C=180°,
∠A=80°
∴∠B+∠C=100°
∵∠B=∠C
∴∠B=∠C=500
如图,在△ABC中,∠ABC=70°,∠C=65°,BD⊥AC于D,求∠ABD,∠CBD的度数。
A
B
C
D
跟踪练习 第四关
作业:
必做题:教材16页习题11.2第1、2题
选做题:
在△ABC中,AB=AC,∠A=40°,∠ABC的角平分线BD交AC于D,求∠ADB 、∠ DBC的度数。
