人教版八年级上册三角形复习课 课件(共20张PPT)
文档属性
| 名称 | 人教版八年级上册三角形复习课 课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 576.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-26 21:47:53 | ||
图片预览



文档简介
(共20张PPT)
三角形复习课
第十一章
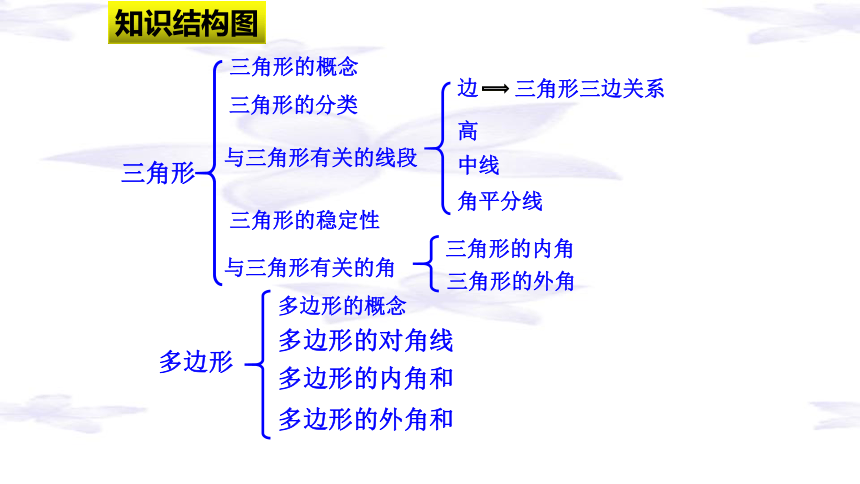
三角形
与三角形有关的角
三角形的分类
三角形的概念
边
三角形的内角
三角形的外角
与三角形有关的线段
中线
高
角平分线
多边形的概念
多边形的对角线
知识结构图
三角形的稳定性
多边形
多边形的内角和
多边形的外角和
三角形三边关系
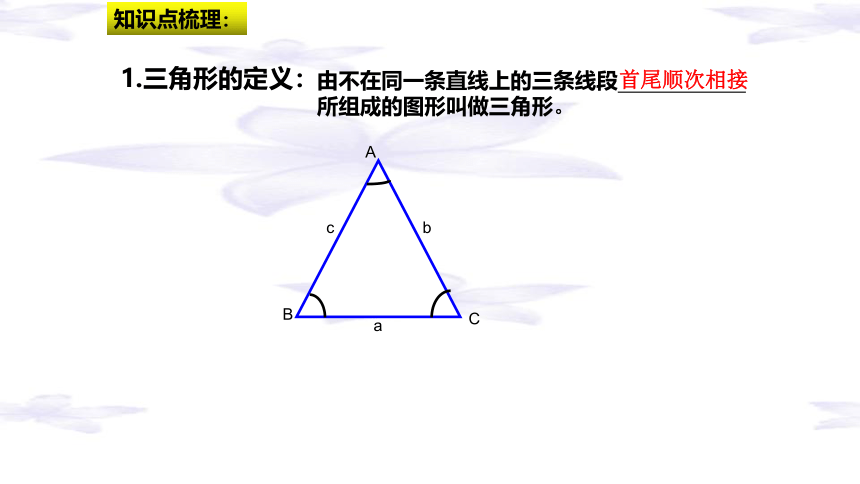
1.三角形的定义:
由不在同一条直线上的三条线段 .所组成的图形叫做三角形。
首尾顺次相接
A
C
B
c
b
a
知识点梳理:
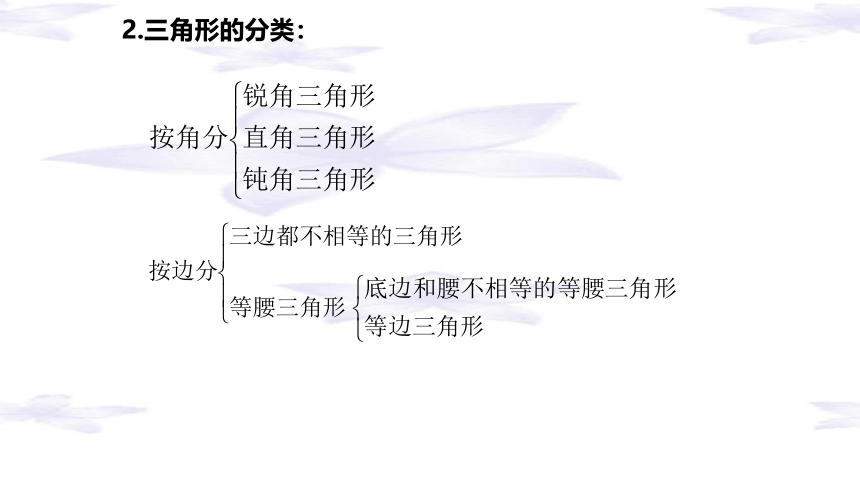
2.三角形的分类:
3.三角形三边的关系
(1)三角形两边的和 第三边,
(2)三角形两边的差 第三边
大于
小于
两边的差<第三边<两边的和
考点一:三角形三边关系
1. (2015 宜昌)已知一个三角形的三边长为3、8、x,则x的取值范围是 。
5例1:(2014 西宁)以下列各组线段长为边,能组成三角形的是( )
A. 2, 2, 4 B. 2, 6, 3 C. 12, 5, 6 D. 7, 3, 6
类比精炼一:
D
2.(2016 长沙)等腰三角形一边的长是 4 另一边的长是7,则它的周长是 。
15或18
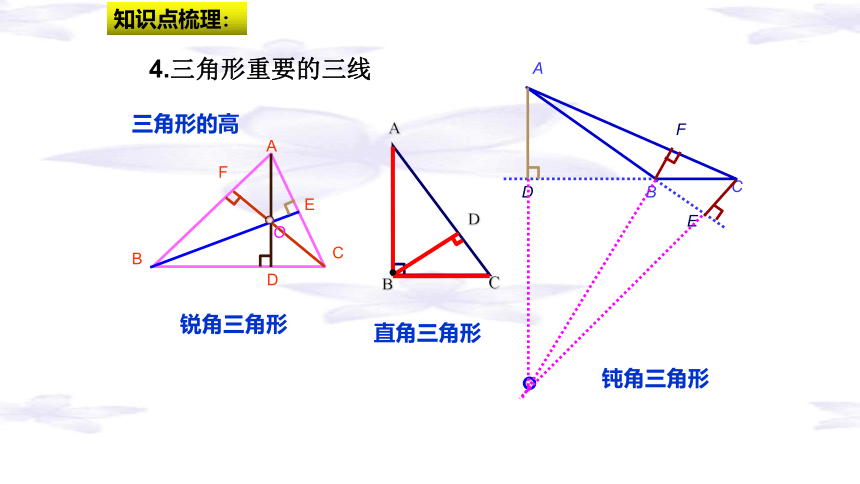
4.三角形重要的三线
三角形的高
知识点梳理:
C
D
O
B
E
F
A
锐角三角形
A
B
C
D
●
直角三角形
A
B
C
D
E
F
钝角三角形
A
B
C
●
●
D
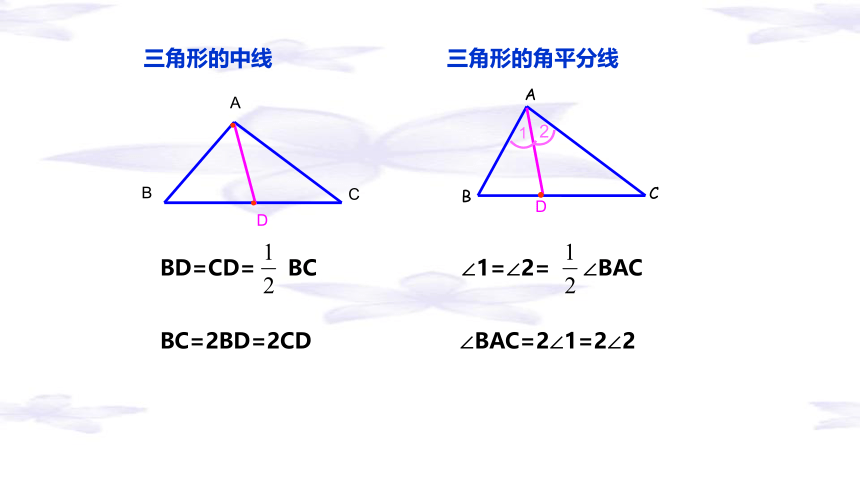
三角形的中线
A
B
D
●
︶
︶
1
2
C
三角形的角平分线
BD=CD= BC
BC=2BD=2CD
∠BAC=2∠1=2∠2
∠1=∠2= ∠BAC
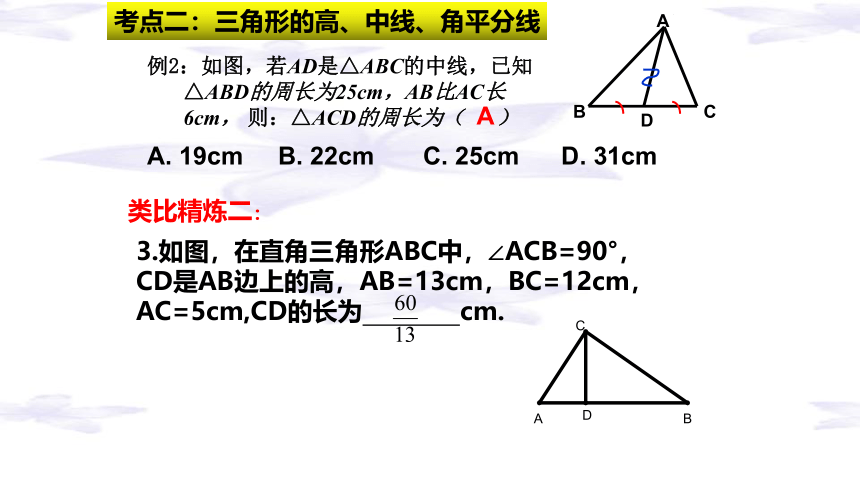
例2:如图,若AD是△ABC的中线,已知△ABD的周长为25cm,AB比AC长6cm, 则:△ACD的周长为( )
A
B
C
D
A. 19cm B. 22cm C. 25cm D. 31cm
类比精炼二:
A
A
B
C
D
考点二:三角形的高、中线、角平分线
3.如图,在直角三角形ABC中,∠ACB=90°,
CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm,CD的长为 cm.
5.三角形的稳定性
三角形 稳定性,
四边形 稳定性.
具有
没有
6.三角形的内角和定理
(1)三角形的三个内角的和等于 ;
(2)直角三角形的两个锐角 。
180°
互余
知识点梳理:
C
B
A
∠A+∠B+∠C=180°
A
B
C
┐
∠A+∠C=90°
例3:如图,在 ABC中,∠C是直角,D是BC上的一点,∠1=40°,∠B=32°,则∠BAD的度数是( )
考点三:三角形的内角和
D
A
B
C
D
A. 40° B. 36° C. 30° D. 18°
类比精炼三:
4.如图,在 ABC中,DE∥BC, ∠A=35°,∠ABC=65°,则∠AED= .
┌
A
B
C
D
E
80°
A
A
C
B
D
1
┌
例4:如图,在△ABC 中,∠ ABC ,∠ ACB 的平
分线BD,CE 交于点O.
若∠ABC =40°,∠ACB =60°,则:
∠BOC = .
A
B
C
O
E
D
130°
变式:若∠A =80°,则∠BOC = .
思考:你能猜想出∠BOC与∠A 之间的数量关系吗?
130°
∠BOC = 90°+ ∠A
7.三角形外角
(2)三角形的一个外角等于 的两个 内角的和;
(3)三角形的一个外角与它相邻的内角 .
与它不相邻
互补
(1)外角的定义:
知识点梳理:
C
A
B
1
∠1=∠A+∠B
∠1+∠ACB=180°
考点四:三角形外角的性质
类比精炼四:
E
A
B
D
F
C
例5:(2013 襄阳)如图,已知直线AB∥CD,
∠C=100°, ∠A=30°,则∠E的度数为( )
A.30° B. 60° C. 70° D. 100°
5.(2014 资阳)如图,若∠A=27°,∠B=45°,∠C=38°,则∠DFE等于( )
A. 120° B.115° C.110° D.105°
C
C
(1)多边形:在平面内,由一些线段首尾顺次相接组成的封闭图形叫做 .
(2)从n边形的一个顶点出发,可以作 条对角线,它们将n边形分为 个三角形,n边形有 条对角线,n边形的内角和等于 .
(3)多边形的外角和等于 .
多边形
(n-3 )
(n-2)
180°x(n-2)
360°
7.多边形的内角和与外角和
知识点梳理:
考点五:多边形的内角和与外角和
例6:(2014 衡阳)若一个多边形的内角和是900°,则这个多边形的边数是( )
A. 5 B. 6 C. 7 D. 8
C
类比精炼五:
6.(2014 巴中)若一个正多边形的一个内角等于135°,那么这个正多边形的边数是 .
8
课堂检测
完成导学案上练习题
课堂小结:
(1)三角形的三边关系
(3)三角形的内角和定理
(2)三角形重要的三线
(5)多边形的内角和与外角和
(4)三角形的外角的性质
1.本节课复习了哪些重要知识点?
2.运用了哪些数学思想方法?
方程思想,化归思想,数形结合思想
五、作业布置
本章复习小测练习
三角形复习课
第十一章
三角形
与三角形有关的角
三角形的分类
三角形的概念
边
三角形的内角
三角形的外角
与三角形有关的线段
中线
高
角平分线
多边形的概念
多边形的对角线
知识结构图
三角形的稳定性
多边形
多边形的内角和
多边形的外角和
三角形三边关系
1.三角形的定义:
由不在同一条直线上的三条线段 .所组成的图形叫做三角形。
首尾顺次相接
A
C
B
c
b
a
知识点梳理:
2.三角形的分类:
3.三角形三边的关系
(1)三角形两边的和 第三边,
(2)三角形两边的差 第三边
大于
小于
两边的差<第三边<两边的和
考点一:三角形三边关系
1. (2015 宜昌)已知一个三角形的三边长为3、8、x,则x的取值范围是 。
5
A. 2, 2, 4 B. 2, 6, 3 C. 12, 5, 6 D. 7, 3, 6
类比精炼一:
D
2.(2016 长沙)等腰三角形一边的长是 4 另一边的长是7,则它的周长是 。
15或18
4.三角形重要的三线
三角形的高
知识点梳理:
C
D
O
B
E
F
A
锐角三角形
A
B
C
D
●
直角三角形
A
B
C
D
E
F
钝角三角形
A
B
C
●
●
D
三角形的中线
A
B
D
●
︶
︶
1
2
C
三角形的角平分线
BD=CD= BC
BC=2BD=2CD
∠BAC=2∠1=2∠2
∠1=∠2= ∠BAC
例2:如图,若AD是△ABC的中线,已知△ABD的周长为25cm,AB比AC长6cm, 则:△ACD的周长为( )
A
B
C
D
A. 19cm B. 22cm C. 25cm D. 31cm
类比精炼二:
A
A
B
C
D
考点二:三角形的高、中线、角平分线
3.如图,在直角三角形ABC中,∠ACB=90°,
CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm,CD的长为 cm.
5.三角形的稳定性
三角形 稳定性,
四边形 稳定性.
具有
没有
6.三角形的内角和定理
(1)三角形的三个内角的和等于 ;
(2)直角三角形的两个锐角 。
180°
互余
知识点梳理:
C
B
A
∠A+∠B+∠C=180°
A
B
C
┐
∠A+∠C=90°
例3:如图,在 ABC中,∠C是直角,D是BC上的一点,∠1=40°,∠B=32°,则∠BAD的度数是( )
考点三:三角形的内角和
D
A
B
C
D
A. 40° B. 36° C. 30° D. 18°
类比精炼三:
4.如图,在 ABC中,DE∥BC, ∠A=35°,∠ABC=65°,则∠AED= .
┌
A
B
C
D
E
80°
A
A
C
B
D
1
┌
例4:如图,在△ABC 中,∠ ABC ,∠ ACB 的平
分线BD,CE 交于点O.
若∠ABC =40°,∠ACB =60°,则:
∠BOC = .
A
B
C
O
E
D
130°
变式:若∠A =80°,则∠BOC = .
思考:你能猜想出∠BOC与∠A 之间的数量关系吗?
130°
∠BOC = 90°+ ∠A
7.三角形外角
(2)三角形的一个外角等于 的两个 内角的和;
(3)三角形的一个外角与它相邻的内角 .
与它不相邻
互补
(1)外角的定义:
知识点梳理:
C
A
B
1
∠1=∠A+∠B
∠1+∠ACB=180°
考点四:三角形外角的性质
类比精炼四:
E
A
B
D
F
C
例5:(2013 襄阳)如图,已知直线AB∥CD,
∠C=100°, ∠A=30°,则∠E的度数为( )
A.30° B. 60° C. 70° D. 100°
5.(2014 资阳)如图,若∠A=27°,∠B=45°,∠C=38°,则∠DFE等于( )
A. 120° B.115° C.110° D.105°
C
C
(1)多边形:在平面内,由一些线段首尾顺次相接组成的封闭图形叫做 .
(2)从n边形的一个顶点出发,可以作 条对角线,它们将n边形分为 个三角形,n边形有 条对角线,n边形的内角和等于 .
(3)多边形的外角和等于 .
多边形
(n-3 )
(n-2)
180°x(n-2)
360°
7.多边形的内角和与外角和
知识点梳理:
考点五:多边形的内角和与外角和
例6:(2014 衡阳)若一个多边形的内角和是900°,则这个多边形的边数是( )
A. 5 B. 6 C. 7 D. 8
C
类比精炼五:
6.(2014 巴中)若一个正多边形的一个内角等于135°,那么这个正多边形的边数是 .
8
课堂检测
完成导学案上练习题
课堂小结:
(1)三角形的三边关系
(3)三角形的内角和定理
(2)三角形重要的三线
(5)多边形的内角和与外角和
(4)三角形的外角的性质
1.本节课复习了哪些重要知识点?
2.运用了哪些数学思想方法?
方程思想,化归思想,数形结合思想
五、作业布置
本章复习小测练习
