华东师大版八年级上册 11.1平方根(第1课时) 课件(共17张PPT)
文档属性
| 名称 | 华东师大版八年级上册 11.1平方根(第1课时) 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 721.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-26 22:08:18 | ||
图片预览






文档简介
(共17张PPT)
第11 章 数的开方
11.1 平方根与立方根
第1课时 平方根
第11章 数的开方
学习目标
1
2
理解数的平方根的概念,知道一个数的平方根的性质. (重点、难点)
会求一个非负数的平方根和算术平方根. (重点)
乘方
求几个相同因式的积的运算叫做乘方。
底数
指数
幂
试比较
知识回顾
问题:如图, 设面积为25cm2的正方形, 其边长为多少呢?
25cm2
5cm
又:面积为16,则边长为:
16
面积为9, 则边长为:
9
面积为5, 则边长为:
5
面积为, 则边长为:
平方根
新课导入
1. 144的平方根是什么?
2. 0的平方根是什么?
3.
的平方根是什么?
4. 有没有平方根?为什么?
0
没有,因为一个数的平方不可能是负数
试一试
例1 求100的平方根.
解:因为=100,,
除了10和-10的平方等于100,
没有其他数的平方是100,
所以100的平方根是10和-10.
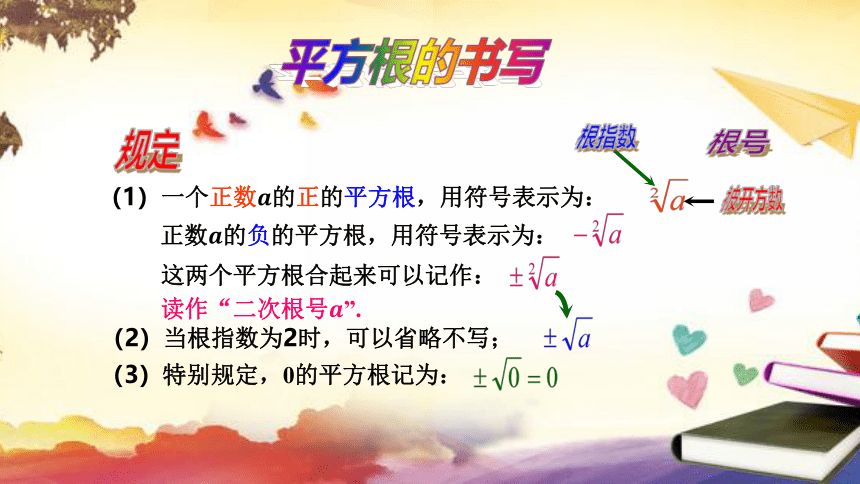
平方根的书写
规定
(1)一个正数的正的平方根,用符号表示为:
根指数
根号
被开方数
正数的负的平方根,用符号表示为:
这两个平方根合起来可以记作:
读作“二次根号”.
(2)当根指数为2时,可以省略不写;
(3)特别规定,0的平方根记为:
平方根的性质
通过刚才的探究活动,大家清楚地感到:
因此,5是25的一个平方根;
因此,4是16的一个平方根;
思考
(1)是否存在其他的数,使它的平方也等于25、16呢?
(2)0的平方根是多少?负数的平方根呢?
(3)通过刚才的研讨,你有何收获?
通过上面的思考,你能发现什么
问题:(1)正数有几个平方根?
(2)0有几个平方根?
(3)负数呢?
有没有一个数的平方是负数?
因为任何实数的平方都为非负数,所以负数没有平方根,也没有算术平方根.
想一想
平方根的性质
(1)一个正数有两个平方根,它们互为相反数;
(2)0有一个平方根,它是0本身;
(3)负数没有平方根.
判断下列各数有没有平方根:
64; ② ; ③ 0.0001;
④; ⑤; ⑥ ;
⑦ 0 ; ⑧ .
要 点 精 析
(1)一个正数的正的平方根就是它的算术平方根.
(2)平方与开平方是互逆运算.开平方与加、减、乘、除、乘方一样是一种运算,即:
运算名称:加、减、乘、除、乘方、开平方(非负数).
运算结果:和、差、积、商、幂、平方根.
(1)81; (2)0.64;
(3) ; (4) ;
1.求下列各数的平方根:
(3) ; (4) .
(1) ; (2) ;
2.解下列方程:
;(4)
;(4)
随堂练习
1.(2019 广西桂林中考)9的平方根是( )
A.3 B.±3 C.-3 D.9
B
2.(2019山东滨州中考)若8与6的和是单项式,则()3的平方根为( )
A.4 B.8 C.±4 D.±8
D
3.一个正数的平方根分别是和,则=________
2
4.是9的平方根,则的值为_______.
3或-3
5.求下列的值:
(1)2=16;(2)92=25.
(2)
求一个数的平方根的运算叫做开平方.
4.开平方的定义:
3.平方根的性质:
(1)一个正数有两个平方根,它们互为相反数.
(2)0有一个平方根,它是0本身.
(3)负数没有平方根.
课后作业
习题1.1 第2题
第11 章 数的开方
11.1 平方根与立方根
第1课时 平方根
第11章 数的开方
学习目标
1
2
理解数的平方根的概念,知道一个数的平方根的性质. (重点、难点)
会求一个非负数的平方根和算术平方根. (重点)
乘方
求几个相同因式的积的运算叫做乘方。
底数
指数
幂
试比较
知识回顾
问题:如图, 设面积为25cm2的正方形, 其边长为多少呢?
25cm2
5cm
又:面积为16,则边长为:
16
面积为9, 则边长为:
9
面积为5, 则边长为:
5
面积为, 则边长为:
平方根
新课导入
1. 144的平方根是什么?
2. 0的平方根是什么?
3.
的平方根是什么?
4. 有没有平方根?为什么?
0
没有,因为一个数的平方不可能是负数
试一试
例1 求100的平方根.
解:因为=100,,
除了10和-10的平方等于100,
没有其他数的平方是100,
所以100的平方根是10和-10.
平方根的书写
规定
(1)一个正数的正的平方根,用符号表示为:
根指数
根号
被开方数
正数的负的平方根,用符号表示为:
这两个平方根合起来可以记作:
读作“二次根号”.
(2)当根指数为2时,可以省略不写;
(3)特别规定,0的平方根记为:
平方根的性质
通过刚才的探究活动,大家清楚地感到:
因此,5是25的一个平方根;
因此,4是16的一个平方根;
思考
(1)是否存在其他的数,使它的平方也等于25、16呢?
(2)0的平方根是多少?负数的平方根呢?
(3)通过刚才的研讨,你有何收获?
通过上面的思考,你能发现什么
问题:(1)正数有几个平方根?
(2)0有几个平方根?
(3)负数呢?
有没有一个数的平方是负数?
因为任何实数的平方都为非负数,所以负数没有平方根,也没有算术平方根.
想一想
平方根的性质
(1)一个正数有两个平方根,它们互为相反数;
(2)0有一个平方根,它是0本身;
(3)负数没有平方根.
判断下列各数有没有平方根:
64; ② ; ③ 0.0001;
④; ⑤; ⑥ ;
⑦ 0 ; ⑧ .
要 点 精 析
(1)一个正数的正的平方根就是它的算术平方根.
(2)平方与开平方是互逆运算.开平方与加、减、乘、除、乘方一样是一种运算,即:
运算名称:加、减、乘、除、乘方、开平方(非负数).
运算结果:和、差、积、商、幂、平方根.
(1)81; (2)0.64;
(3) ; (4) ;
1.求下列各数的平方根:
(3) ; (4) .
(1) ; (2) ;
2.解下列方程:
;(4)
;(4)
随堂练习
1.(2019 广西桂林中考)9的平方根是( )
A.3 B.±3 C.-3 D.9
B
2.(2019山东滨州中考)若8与6的和是单项式,则()3的平方根为( )
A.4 B.8 C.±4 D.±8
D
3.一个正数的平方根分别是和,则=________
2
4.是9的平方根,则的值为_______.
3或-3
5.求下列的值:
(1)2=16;(2)92=25.
(2)
求一个数的平方根的运算叫做开平方.
4.开平方的定义:
3.平方根的性质:
(1)一个正数有两个平方根,它们互为相反数.
(2)0有一个平方根,它是0本身.
(3)负数没有平方根.
课后作业
习题1.1 第2题
