北师大版 八年级下册 第四章 因式分解 学案(无答案)
文档属性
| 名称 | 北师大版 八年级下册 第四章 因式分解 学案(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 188.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-27 10:34:06 | ||
图片预览




文档简介
第四讲 因式分解
第1课时 提公因式法
知识点 1 公因式的定义
1.多项式3x2-6x中各项的公因式是( )
A.3 B.x C.3x D.3x2
2.(1)单项式12x12y3与8x10y6的公因式是 ;
(2)多项式-xy2z3+xz2中各项的公因式是 ;
(3)多项式2x2+12xy2+8xy3中各项的公因式是 .
知识点 2 提公因式(单项式)因式分解
3.下列能用提公因式法因式分解的是( )
A.x2-y B.x2+2x C.x2+y2 D.x2-xy+y2
4.把多项式a2-2a因式分解,正确的是( )
A.a(a-2) B.a(a+2) C.a(a2-2) D.a(2-a)
5.把下列各式因式分解:
(1)2a2-12a= ;
(2)a2+ab-a= ;
(3)-a2b+5ab-9b= .
6.把下列各式因式分解:
(1)-5x+5xy; (2)2a2b+4ab2-6ab; (3)-6x3y2+12x2y3-6x2y2.
7.多项式x2m-xm提取公因式xm后,另一个因式是( )
A.x2-1 B.xm-1 C.xm D.x2m-1
8.如相邻两边长分别为a,b的长方形的周长为10,面积为6.
(1)a+b= ,ab= ;
(2)求a3b2+a2b3的值.
9.因式分解:
(1)6x4y3-3x2y2z-2x3y2; (2)-10a2bc+15bc2-20ab2c.
10.已知2x-y=,xy=2,求2x4y3-x3y4的值.
知识点 3 提公因式(多项式)因式分解
1.把5(a-b)+m(a-b)提公因式后一个因式是(a-b),则另一个因式是( )
A.5+m B.5-m C.-5+m D.-5-m
2.在下列各式中,从左到右的变形错误的是( )
A.y-x=-(x-y) B.(y-x)2=(x-y)2
C.(y-x)3=-(x-y)3 D.(y-x)3=(x-y)3
3.把下列各式因式分解:
(1)3a(x+4)-2(x+4); (2)a(a-b)+(a-b); (3)m(n-m)-n(m-n); (4)a(a-b)-(b-a)2.
知识点 4 提公因式法因式分解的应用
4.若a,b互为相反数,则a(x-2y)-b(2y-x)的值为 .
5.先因式分解,再求值.
(1)4x(m-2)-3x(m-2),其中x=15,m=6; (2)(a-2)2-5(2-a),其中a=-2.
6.若m-n=-1,则(m-n)2-2m+2n的值是( )
A.3 B.2 C.1 D.-1
7.因式分解:x(x-2)-x+2= .
8.因式分解:m(n-2)-m2(2-n)= .
课堂小测
1.把代数式,分解因式,结果正确的是( )
A. B. C. D.
2.下列各式从左到右的变形(1);(2);
(3);(4),其中是因式分解的个数是( )
A.1个 B.2个 C.3个 D.4个
3.如果多项式的一个因式是,那么另一个因式是( )
A. B. C. D.
4.用提取公因式法分解因式正确的是( )
A. B.
C. D.
的公因式是( )
A. B. C. D.
6.把多项式分解因式的结果是( )
A. B. C. D.
第2课时 公式法
公式1 利用平方差公式因式分解
知识点 1 利用平方差公式因式分解
1.下列多项式中,能运用平方差公式因式分解的是( )
A.a2+b2 B.2a-b2 C.a2-b2 D.-a2-b2
变式:下列各式中能用平方差公式分解因式的是( )
A. B. C. D.
2.下列因式分解中,结果正确的是( )
A.x2-25=(x+5)(x-5) B.1-(x+2)2=(x+1)(x+3)
C.4m2-n2=(2m+n)(m-n) D.x2-4=(x-2)2
若x2-9=(x+a)(x+3),则a= .
4.因式分解:-0.81+121a2= .
5.把下列各式因式分解:
(1)x2-16; (2)49m2-n2; (3)(2x+3y)2-1; (4)49m2-(2m+n)2.
知识点 2 先提取公因式,再利用平方差公式因式分解
(2020宁波)因式分解:2a2-18= .
7.把下列各式因式分解:
(1)x3y-xy3; (2)2a2(n-m)+8(m-n).
知识点 3 用平方差公式因式分解的应用
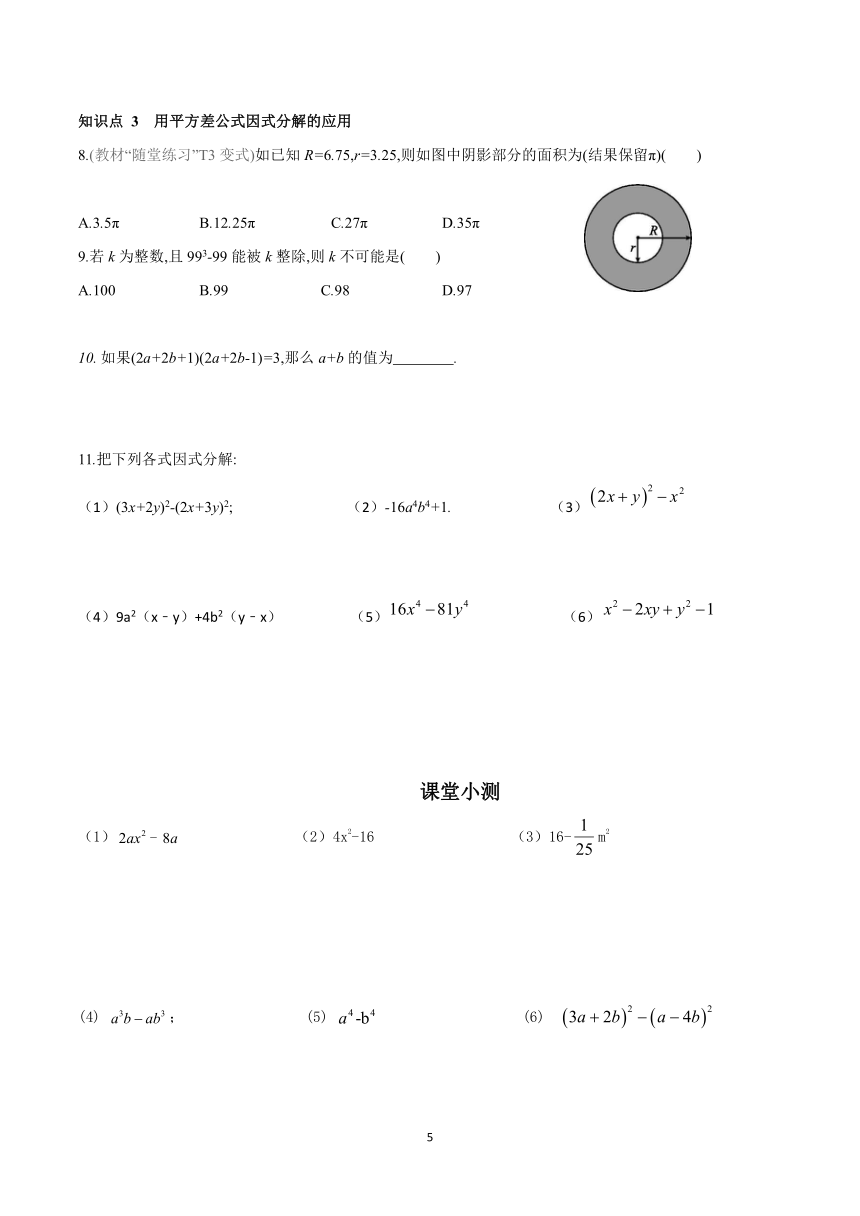
8.(教材“随堂练习”T3变式)如已知R=6.75,r=3.25,则如图中阴影部分的面积为(结果保留π)( )
A.3.5π B.12.25π C.27π D.35π
9.若k为整数,且993-99能被k整除,则k不可能是( )
A.100 B.99 C.98 D.97
如果(2a+2b+1)(2a+2b-1)=3,那么a+b的值为 .
11.把下列各式因式分解:
(1)(3x+2y)2-(2x+3y)2; (2)-16a4b4+1. (3)
(4)9a2(x﹣y)+4b2(y﹣x) (5) (6)
课堂小测
(1) (2)4x2-16 (3)16-m2
(4) ; (5) (6)
公式2 利用完全平方公式因式分解
知识点 1 利用完全平方公式因式分解
1.因式分解x2-2x+1的最终结果是( )
A.x(x-2)+1 B.(x+1)(x-2) C.(x-1)2 D.(x+1)2
2.下列各式中能用完全平方公式进行因式分解的是( )
A.x2+x+1 B.x2+2x-1 C.x2-1 D.x2-6x+9
3.小华同学利用完全平方公式对下列式子进行因式分解,你认为正确的是( )
A.x2+4x+4=(x+4)2 B.4x2-2x+1=(2x-1)2
C.-a2-b2+2ab=-(a-b)2 D.9-6(m-n)+(m-n)2=(3-m-n)2
4.计算1002-2×100×99+992的值为( )
A.0 B.1 C.-1 D.39601
5.把下列各式因式分解:
(1)x2+6x+9; (2)-x2+2x-1; (3)m2-mn+n2; (4)9(a-b)2+42(a-b)+49.
知识点 2 先提取公因式,再利用完全平方公式因式分解
6.多项式2m2-12m+18因式分解,正确的结果是( )
A.2m2(m+3) B.2(m-3)2 C.2m(m+3) D.2(m2-6m+9)
已知a+b=3,ab=2,则a3b+2a2b2+ab3的值为 .
8.把下列各式因式分解:
(1)x3-2x2y+xy2; (2)2a2b-a3-ab2; (3)-3x2+2x-.
9.如果多项式9x2-mxy+16y2能因式分解为(a+b)2的形式,则m的值为( )
A.12 B.±12 C.24 D.±24
10.a2+25b2=6a-10b-10,则a+5b的值为 .
11.把下列各式因式分解:
(1)x2(y2-1)+2x(y2-1)+(y2-1); (2)(x2-1)2-6(x2-1)+9. (3)
(4) (5) (6)
课堂小测
若是完全平方式,那么等于( ).
A. B. C. D.
2.下列多项式中,不能用完全平方公式分解因式的是( ).
A. B. C. D.
3.若是完全平方式,那么.
4.分解因式:
(1) (2); (3)
世纪*教育网
第3课时 十字相乘法
【学习目标】:
1.能熟练地把形如的二次三项式因式分解;
2.通过对规律的探索,提升自己从特殊到一般,从具体到抽象的思维品质。
【学习重点】: 熟练地把形如的二次三项式因式分解
【学习难点】:在分解形如的二次三项式时能准确找到各个因式。
1、提出问题,创设情境:
问题(1):计算
(1) (2) (3) (4)
2、问题:怎样将这类题目又快又准地解答出来的呢?
=
【二、研学】
探究一:把下列完全平方式因式分解
(1) (2) (3) (4)
探究二:把下列各式因式分解:
(1)
探究三:把下列各式因式分解
(2)
探究x:把下列各式因式分解
(1) (2)
讨论:(1)当二次项系数为1时如何利用十字相乘法分解因式?
(2)当二次项系数不为1时如何利用十字相乘法分解因式?
【三、评学】:
1、将下列各式进行因式分解( )
(1) (2) (3) (4)
拓展延伸:
(1) (2) (3)
基础巩固
1. 如果,那么p等于 ( )
A.ab B.a+b C.-ab D.-(a+b)
2. 如果,则b为 ( )
A.5 B.-6 C.-5 D.6
多项式可分解为(x-5)(x-b),则a,b的值分别为( )
A.10和-2 B.-10和2 C.10和2 D.-10和-2
不能用十字相乘法分解的是 ( )
A. B. C. D.
分解结果等于(x+y-4)(2x+2y-5)的多项式是 ( )
A. B.
C. D.
6. 将下述多项式分解后,有相同因式x-1的多项式有 ( )
①; ②; ③;
④; ⑤; ⑥
A.2个 B.3个 C.4个 D.5个
能力提升
1. 把下列各式分解因式:
(1); (2); (3);
(4); (5); (6).
课堂小测
1. 把下列各式分解因式:
(1) (2)
(3 ) ; (4) ;
(5); (6);
把下列各式分解因式(可另外附纸)
(1); (2); (3);
(4) ; (5); (6);
(7); (81); (9);
(10); (11); (12);
(13); (14); (15);
(16) ;
第1课时 提公因式法
知识点 1 公因式的定义
1.多项式3x2-6x中各项的公因式是( )
A.3 B.x C.3x D.3x2
2.(1)单项式12x12y3与8x10y6的公因式是 ;
(2)多项式-xy2z3+xz2中各项的公因式是 ;
(3)多项式2x2+12xy2+8xy3中各项的公因式是 .
知识点 2 提公因式(单项式)因式分解
3.下列能用提公因式法因式分解的是( )
A.x2-y B.x2+2x C.x2+y2 D.x2-xy+y2
4.把多项式a2-2a因式分解,正确的是( )
A.a(a-2) B.a(a+2) C.a(a2-2) D.a(2-a)
5.把下列各式因式分解:
(1)2a2-12a= ;
(2)a2+ab-a= ;
(3)-a2b+5ab-9b= .
6.把下列各式因式分解:
(1)-5x+5xy; (2)2a2b+4ab2-6ab; (3)-6x3y2+12x2y3-6x2y2.
7.多项式x2m-xm提取公因式xm后,另一个因式是( )
A.x2-1 B.xm-1 C.xm D.x2m-1
8.如相邻两边长分别为a,b的长方形的周长为10,面积为6.
(1)a+b= ,ab= ;
(2)求a3b2+a2b3的值.
9.因式分解:
(1)6x4y3-3x2y2z-2x3y2; (2)-10a2bc+15bc2-20ab2c.
10.已知2x-y=,xy=2,求2x4y3-x3y4的值.
知识点 3 提公因式(多项式)因式分解
1.把5(a-b)+m(a-b)提公因式后一个因式是(a-b),则另一个因式是( )
A.5+m B.5-m C.-5+m D.-5-m
2.在下列各式中,从左到右的变形错误的是( )
A.y-x=-(x-y) B.(y-x)2=(x-y)2
C.(y-x)3=-(x-y)3 D.(y-x)3=(x-y)3
3.把下列各式因式分解:
(1)3a(x+4)-2(x+4); (2)a(a-b)+(a-b); (3)m(n-m)-n(m-n); (4)a(a-b)-(b-a)2.
知识点 4 提公因式法因式分解的应用
4.若a,b互为相反数,则a(x-2y)-b(2y-x)的值为 .
5.先因式分解,再求值.
(1)4x(m-2)-3x(m-2),其中x=15,m=6; (2)(a-2)2-5(2-a),其中a=-2.
6.若m-n=-1,则(m-n)2-2m+2n的值是( )
A.3 B.2 C.1 D.-1
7.因式分解:x(x-2)-x+2= .
8.因式分解:m(n-2)-m2(2-n)= .
课堂小测
1.把代数式,分解因式,结果正确的是( )
A. B. C. D.
2.下列各式从左到右的变形(1);(2);
(3);(4),其中是因式分解的个数是( )
A.1个 B.2个 C.3个 D.4个
3.如果多项式的一个因式是,那么另一个因式是( )
A. B. C. D.
4.用提取公因式法分解因式正确的是( )
A. B.
C. D.
的公因式是( )
A. B. C. D.
6.把多项式分解因式的结果是( )
A. B. C. D.
第2课时 公式法
公式1 利用平方差公式因式分解
知识点 1 利用平方差公式因式分解
1.下列多项式中,能运用平方差公式因式分解的是( )
A.a2+b2 B.2a-b2 C.a2-b2 D.-a2-b2
变式:下列各式中能用平方差公式分解因式的是( )
A. B. C. D.
2.下列因式分解中,结果正确的是( )
A.x2-25=(x+5)(x-5) B.1-(x+2)2=(x+1)(x+3)
C.4m2-n2=(2m+n)(m-n) D.x2-4=(x-2)2
若x2-9=(x+a)(x+3),则a= .
4.因式分解:-0.81+121a2= .
5.把下列各式因式分解:
(1)x2-16; (2)49m2-n2; (3)(2x+3y)2-1; (4)49m2-(2m+n)2.
知识点 2 先提取公因式,再利用平方差公式因式分解
(2020宁波)因式分解:2a2-18= .
7.把下列各式因式分解:
(1)x3y-xy3; (2)2a2(n-m)+8(m-n).
知识点 3 用平方差公式因式分解的应用
8.(教材“随堂练习”T3变式)如已知R=6.75,r=3.25,则如图中阴影部分的面积为(结果保留π)( )
A.3.5π B.12.25π C.27π D.35π
9.若k为整数,且993-99能被k整除,则k不可能是( )
A.100 B.99 C.98 D.97
如果(2a+2b+1)(2a+2b-1)=3,那么a+b的值为 .
11.把下列各式因式分解:
(1)(3x+2y)2-(2x+3y)2; (2)-16a4b4+1. (3)
(4)9a2(x﹣y)+4b2(y﹣x) (5) (6)
课堂小测
(1) (2)4x2-16 (3)16-m2
(4) ; (5) (6)
公式2 利用完全平方公式因式分解
知识点 1 利用完全平方公式因式分解
1.因式分解x2-2x+1的最终结果是( )
A.x(x-2)+1 B.(x+1)(x-2) C.(x-1)2 D.(x+1)2
2.下列各式中能用完全平方公式进行因式分解的是( )
A.x2+x+1 B.x2+2x-1 C.x2-1 D.x2-6x+9
3.小华同学利用完全平方公式对下列式子进行因式分解,你认为正确的是( )
A.x2+4x+4=(x+4)2 B.4x2-2x+1=(2x-1)2
C.-a2-b2+2ab=-(a-b)2 D.9-6(m-n)+(m-n)2=(3-m-n)2
4.计算1002-2×100×99+992的值为( )
A.0 B.1 C.-1 D.39601
5.把下列各式因式分解:
(1)x2+6x+9; (2)-x2+2x-1; (3)m2-mn+n2; (4)9(a-b)2+42(a-b)+49.
知识点 2 先提取公因式,再利用完全平方公式因式分解
6.多项式2m2-12m+18因式分解,正确的结果是( )
A.2m2(m+3) B.2(m-3)2 C.2m(m+3) D.2(m2-6m+9)
已知a+b=3,ab=2,则a3b+2a2b2+ab3的值为 .
8.把下列各式因式分解:
(1)x3-2x2y+xy2; (2)2a2b-a3-ab2; (3)-3x2+2x-.
9.如果多项式9x2-mxy+16y2能因式分解为(a+b)2的形式,则m的值为( )
A.12 B.±12 C.24 D.±24
10.a2+25b2=6a-10b-10,则a+5b的值为 .
11.把下列各式因式分解:
(1)x2(y2-1)+2x(y2-1)+(y2-1); (2)(x2-1)2-6(x2-1)+9. (3)
(4) (5) (6)
课堂小测
若是完全平方式,那么等于( ).
A. B. C. D.
2.下列多项式中,不能用完全平方公式分解因式的是( ).
A. B. C. D.
3.若是完全平方式,那么.
4.分解因式:
(1) (2); (3)
世纪*教育网
第3课时 十字相乘法
【学习目标】:
1.能熟练地把形如的二次三项式因式分解;
2.通过对规律的探索,提升自己从特殊到一般,从具体到抽象的思维品质。
【学习重点】: 熟练地把形如的二次三项式因式分解
【学习难点】:在分解形如的二次三项式时能准确找到各个因式。
1、提出问题,创设情境:
问题(1):计算
(1) (2) (3) (4)
2、问题:怎样将这类题目又快又准地解答出来的呢?
=
【二、研学】
探究一:把下列完全平方式因式分解
(1) (2) (3) (4)
探究二:把下列各式因式分解:
(1)
探究三:把下列各式因式分解
(2)
探究x:把下列各式因式分解
(1) (2)
讨论:(1)当二次项系数为1时如何利用十字相乘法分解因式?
(2)当二次项系数不为1时如何利用十字相乘法分解因式?
【三、评学】:
1、将下列各式进行因式分解( )
(1) (2) (3) (4)
拓展延伸:
(1) (2) (3)
基础巩固
1. 如果,那么p等于 ( )
A.ab B.a+b C.-ab D.-(a+b)
2. 如果,则b为 ( )
A.5 B.-6 C.-5 D.6
多项式可分解为(x-5)(x-b),则a,b的值分别为( )
A.10和-2 B.-10和2 C.10和2 D.-10和-2
不能用十字相乘法分解的是 ( )
A. B. C. D.
分解结果等于(x+y-4)(2x+2y-5)的多项式是 ( )
A. B.
C. D.
6. 将下述多项式分解后,有相同因式x-1的多项式有 ( )
①; ②; ③;
④; ⑤; ⑥
A.2个 B.3个 C.4个 D.5个
能力提升
1. 把下列各式分解因式:
(1); (2); (3);
(4); (5); (6).
课堂小测
1. 把下列各式分解因式:
(1) (2)
(3 ) ; (4) ;
(5); (6);
把下列各式分解因式(可另外附纸)
(1); (2); (3);
(4) ; (5); (6);
(7); (81); (9);
(10); (11); (12);
(13); (14); (15);
(16) ;
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
