2022-2023学年人教A版2019高中数学必修1 第三章 函数的概念与性质 习题课 反比例函数、对勾函数 课件 (75张PPT)
文档属性
| 名称 | 2022-2023学年人教A版2019高中数学必修1 第三章 函数的概念与性质 习题课 反比例函数、对勾函数 课件 (75张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-27 11:10:01 | ||
图片预览











文档简介
(共75张PPT)
习题课 反比例函数、对勾函数
第三章 函数的概念与性质
学习目标
1.掌握反比例函数和对勾函数的图象和性质.
2.能通过构造函数解决实际问题.
课时对点练
一、反比例函数的图象和性质
二、对勾函数的图象和性质
三、对勾函数的综合运用
随堂演练
内容索引
反比例函数的图象和性质
一
问题1 反比例函数的一般形式是什么?
问题2 反比例函数的图象会过坐标原点吗?
提示 不会,因为x≠0.
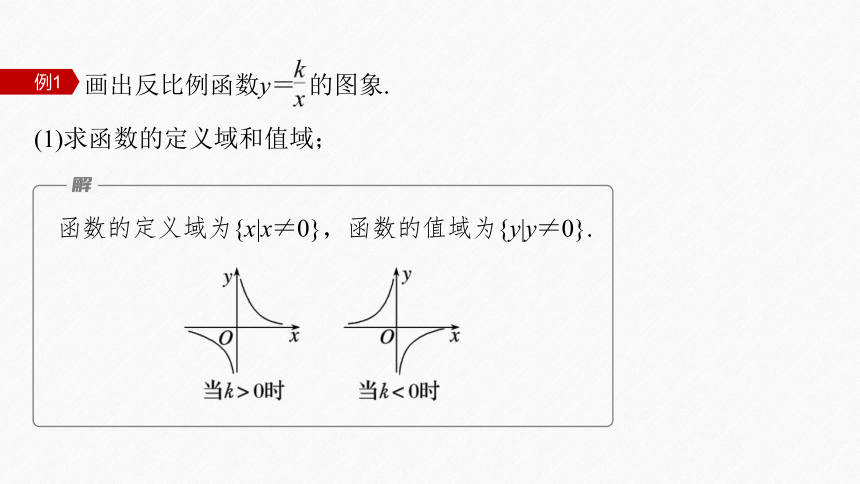
画出反比例函数y= 的图象.
(1)求函数的定义域和值域;
例1
函数的定义域为{x|x≠0},函数的值域为{y|y≠0}.
(2)判断函数的单调性和奇偶性.
令y=f(x),当k>0时,f(x)的单调递减区间为(-∞,0)和(0,+∞),没有单调递增区间,证明如下:
当x>0时, x1,x2∈(0,+∞)且x1∵k>0,x1>0,x2>0,x1∴f(x1)-f(x2)>0,即f(x1)>f(x2),∴f(x)在(0,+∞)上单调递减,
同理当x<0时,f(x)在(-∞,0)上单调递减.
当k<0时,f(x)的单调递增区间为(-∞,0)和(0,+∞),没有单调递减区间(证明略).
f(x)为奇函数.
研究反比例函数的几个方面
(1)函数的定义域和值域可以由图象直接得到.
(2)由图象或者单调性的定义可以判断函数的单调性,但一定要注意两个单调递增(减)区间的连接方法.
(3)由图象或者奇偶性的定义可以判断函数的奇偶性.
(4)函数图象关于(0,0)中心对称.
反思感悟
作出y= (-2≤x<1且x≠0)的图象,并指出其值域和单调区间.
跟踪训练1
由题意知函数y= (-2≤x<1且x≠0)的图象为反比例函数图象的一部分,
所以该函数图象如图:
由图象可知,函数y= (-2≤x<1且x≠0)的值域为(-∞,-1]∪(2,+∞).
单调递减区间为[-2,0)和(0,1),没有单调递增区间.
对勾函数的图象和性质
二
问题3 观察函数y=x+ 解析式的特点,你想到了什么?
提示 学习了幂函数,类比实数的加、减、乘、除运算,我们对幂函数也进行相关的运算,得到了新的函数y=x+ .
问题4 大家讨论一下,如何作出该函数的图象?
提示 借助计算机软件,我们绘制出它的图象.
问题5 观察函数图象,你能发现函数图象有什么特点吗?
提示 发现该函数图象介于y=x和y轴之间,且图象无限接近y=x和y轴,函数图象像两个勾子一样,故称此类函数为“对勾函数”.
问题6 结合函数的解析式和函数图象,你能得出f(x)=x+ 的哪些性质?
提示 (1)定义域:∵x≠0,
(5)最大值、最小值:由函数的值域可知,函数无最大、最小值,但是当x>0时,函数有最小值为2,当x<0时,函数有最大值为-2.
(6)对称性:由函数的奇偶性可知,函数图象关于(0,0)成中心对称.
探究函数f(x)=x+ (a>0)的性质,并画出它的简图(单调性需证明,
其余性质列出即可).
例2
(1)定义域:{x|x≠0};
(3)奇偶性:奇函数;
所以x1-x2<0,0所以f(x1)-f(x2)>0,
即f(x1)>f(x2).
因为x1-x2<0,x1x2>a,
所以f(x1)-f(x2)<0,所以f(x1)其图象如图所示.
延伸探究 当a<0时,探究该函数的性质,并画出函数的简图(单调性需证明,其余性质列出即可).
(1)定义域:{x|x≠0};
(2)值域:R;
(3)奇偶性:奇函数;
(4)函数f(x)在区间(-∞,0),(0,+∞)上单调递增,证明如下:
任取x1,x2∈(0,+∞),且x1因为0所以f(x1)-f(x2)<0,
即f(x1)所以函数f(x)在区间(0,+∞)上单调递增;
同理可知,函数f(x)在区间(-∞,0)上单调递增.
其简图如图所示.
(1)x∈[1,3],f(x)的最小值是____;
跟踪训练2
2
∵f(x)在[1,3]上单调递增,∴f(x)的最小值为f(1)=2.
∴最小值为f(1)=2,
对勾函数的综合运用
三
问题7 应用基本不等式求最值应注意哪些?
提示 一正,二定,三相等.
(1)当a=4时,求函数f(x)在x∈(0,+∞)上的最小值;
例3
∴f(x)的最小值为2.
(2)当a>0时,求函数f(x)在[2,+∞)上的最小值.
∴f(x1)-f(x2)>0,即f(x1)>f(x2),
设f(x)的最小值为g(a),
求对勾函数的最值问题,可以利用函数的单调性研究,也可以利用基本不等式.
反思感悟
(1)已知x>0,求y= 的最大值,并求此时x的值.
跟踪训练3
(2)已知x≥2,求y=x+ 的最小值(提示:利用图象助解).
课堂
小结
1.知识清单:
(1)反比例函数的图象和性质.
(2)对勾函数的图象和性质.
2.方法归纳:分类讨论、数形结合.
3.常见误区:研究函数的性质一定先确定函数的定义域.
随堂演练
1.函数y= ,当x>0时,y随x的增大而增大,那么m的取值范围是
A.m<3 B.m>3
C.m<-3 D.m>-3
√
1
2
3
4
在反比例函数y= 中,若k>0,在x>0时,y随x的增大而减小,若k<0,
在x>0时,y随x的增大而增大,所以由题意得m-3<0,m<3.
1
2
3
4
2.(多选)已知函数y= ,下列结论中正确的是
A.其图象经过点(3,1)
B.其图象分别位于第一、三象限
C.当x>0时,y随x的增大而减小
D.当x>1时,y>3
√
√
√
1
2
3
4
反比例函数y= ,当x=3时,y=1,故A正确;
因为y= 分子大于0,所以图象在第一、三象限,故B正确;
反比例函数在第一、三象限上都单调递减,所以C正确;
因为在(0,+∞) 上,y= 单调递减,所以当x>1时,01
2
3
4
3.已知点P(a,m),Q(b,n)都在函数 的图象上,且a<0<b,则下列结论一定正确的是
A.m+n<0 B.m+n>0
C.m>n D.m<n
√
1
2
3
4
∵a<0,
∴P(a,m)在第二象限,
∴m>0.
∵b>0,
∴Q(b,n)在第四象限,
∴n<0.
∴n<0<m,即m>n.
1
2
3
4
(0,2)
1
2
3
4
∴实数t的取值范围为(0,2).
课时对点练
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
A.A=B B.A=C
C.B=C D.A=B=C
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2. 某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(千帕)是气球体积V(立方米)的反比例函数,其图象如图所示,则这个函数的解析式为
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.函数f(x)=x+ 在区间[1,3]上的最大值是
A.3 B.5 C.4 D.
√
由对勾函数的图象的特点可知,x=2时函数有最小值,x=1时,函数有最大值为5.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.函数f(x)=x+ (a>0,x∈R,x≠0)的奇偶性为
A.奇函数 B.偶函数
C.非奇非偶函数 D.无法判断
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.函数g(x)=x+ 的单调递减区间为
A.(-2,0)∪(0,2) B.(-2,2)
C.(-2,0)和(0,2) D.(-∞,-2)和(2,+∞)
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
则函数在区间(1,+∞)上单调递减.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
再向上平移1个单位长度得到的,
∴对称中心为(-1,1).
(-1,1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.在平面直角坐标系中,函数y=-x+a与函数y= 的图象有两个公共点,
则实数a的取值范围是 ____________.
a<-2或a>2
函数y=-x+a与反比例函数y= 的图象有两个公共点,
则方程组有两个解,即方程①有两个不同的解,
Δ=a2-4>0,a<-2或a>2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.作出函数y= 的图象,并写出函数的单调区间和值域.
函数在(-∞,2)和(2,+∞)上单调递减.
故单调递减区间为(-∞,2)和(2,+∞),无单调递增区间.值域为(-∞,1)∪(1,+∞).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.一家货物公司计划租地建造仓库储存货物,经过市场调查了解到下列信息:每月土地占地费y1(单位:万元)与仓库到车站的距离x(单位:km)成反比,每月库存货物费y2(单位:万元)与(4x+1)成正比;若在距离车站10 km处建仓库,则y1与y2分别为2万元和8.2万元.记两项费用之和为w.
(1)求w关于x的解析式;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∵每月土地占地费y1(单位:万元)与仓库到车站的距离x(单位:km)成反比,
∵每月库存货物费y2(单位:万元)与(4x+1)成正比,
∴可设y2=(4x+1)k2,
又∵在距离车站10 km处建仓库,则y1与y2分别为2万元和8.2万元,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)这家公司应该把仓库建在距离车站多少千米处,才能使两项费用之和最小?求出最小值.
∴这家公司应该把仓库建在距离车站5千米处,才能使两项费用之和最小,最小值为8.2万元.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
11.函数f(x)= (x∈R)的值域是
A.(0,1) B.(0,1]
C.[0,1) D.[0,1]
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∵x<0,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.一批救灾物资随26辆汽车从某市以v km/h的速度送达灾区,已知运送的路线长400 km,为了安全起见,两辆汽车的间距不得小于 ,那么这批物资全部到达灾区最少需要
A.5 h B.10 h C.15 h D.20 h
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
设这批物资全部到达灾区的时间为t h,
故这批物资全部到达灾区最少需要10 h.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.函数f(x)=x- 的单调递增区间为_____________________.
画出函数图象如图,可知函数f(x)的单调递增区间为(-∞,0)和(0,+∞).
(-∞,0)和(0,+∞)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
15.已知函数f(x)= 若存在0=f(x2)=f(x3)=f(x4),则x1x2x3x4的取值范围是__________.
(96,100)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
可得函数图象如图所示.
由图可知,当y∈(4,5)时,存在0不妨令此时y=a,则对于x1,x2满足方程x+ =a,即x2-ax+4=0,所以x1x2=4;对于x3,x4满足方程-x2+10x-20=a,即-x2+10x-20-a=0,所以x3+x4=10,则有x4=10-x3,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴x1x2x3x4=4x3x4=4x3(10-x3)=-4(x3-5)2+100,
其中x3∈(4,5),则-4(x3-5)2+100∈(96,100),
即x1x2x3x4∈(96,100).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为x∈[0,1],则t=2x+1∈[1,3].
由已知性质可知u(t)在[1,2]上单调递减,在[2,3]上单调递增.
所以f(x)max=-3,所以值域为[-4,-3].
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)对于(1)中的函数f(x)和函数g(x)=-x-2a,若对任意x1∈[0,1],总存在x2∈[0,1],使得g(x2)=f(x1)成立,求实数a的值.
因为g(x)=-x-2a为减函数,所以当x∈[0,1]时,g(x)∈[-1-2a,-2a].
因为对任意x1∈[0,1],总存在x2∈[0,1],使得g(x2)=f(x1)成立,
所以f(x)的值域是g(x)值域的子集,
本课结束
习题课 反比例函数、对勾函数
第三章 函数的概念与性质
学习目标
1.掌握反比例函数和对勾函数的图象和性质.
2.能通过构造函数解决实际问题.
课时对点练
一、反比例函数的图象和性质
二、对勾函数的图象和性质
三、对勾函数的综合运用
随堂演练
内容索引
反比例函数的图象和性质
一
问题1 反比例函数的一般形式是什么?
问题2 反比例函数的图象会过坐标原点吗?
提示 不会,因为x≠0.
画出反比例函数y= 的图象.
(1)求函数的定义域和值域;
例1
函数的定义域为{x|x≠0},函数的值域为{y|y≠0}.
(2)判断函数的单调性和奇偶性.
令y=f(x),当k>0时,f(x)的单调递减区间为(-∞,0)和(0,+∞),没有单调递增区间,证明如下:
当x>0时, x1,x2∈(0,+∞)且x1
同理当x<0时,f(x)在(-∞,0)上单调递减.
当k<0时,f(x)的单调递增区间为(-∞,0)和(0,+∞),没有单调递减区间(证明略).
f(x)为奇函数.
研究反比例函数的几个方面
(1)函数的定义域和值域可以由图象直接得到.
(2)由图象或者单调性的定义可以判断函数的单调性,但一定要注意两个单调递增(减)区间的连接方法.
(3)由图象或者奇偶性的定义可以判断函数的奇偶性.
(4)函数图象关于(0,0)中心对称.
反思感悟
作出y= (-2≤x<1且x≠0)的图象,并指出其值域和单调区间.
跟踪训练1
由题意知函数y= (-2≤x<1且x≠0)的图象为反比例函数图象的一部分,
所以该函数图象如图:
由图象可知,函数y= (-2≤x<1且x≠0)的值域为(-∞,-1]∪(2,+∞).
单调递减区间为[-2,0)和(0,1),没有单调递增区间.
对勾函数的图象和性质
二
问题3 观察函数y=x+ 解析式的特点,你想到了什么?
提示 学习了幂函数,类比实数的加、减、乘、除运算,我们对幂函数也进行相关的运算,得到了新的函数y=x+ .
问题4 大家讨论一下,如何作出该函数的图象?
提示 借助计算机软件,我们绘制出它的图象.
问题5 观察函数图象,你能发现函数图象有什么特点吗?
提示 发现该函数图象介于y=x和y轴之间,且图象无限接近y=x和y轴,函数图象像两个勾子一样,故称此类函数为“对勾函数”.
问题6 结合函数的解析式和函数图象,你能得出f(x)=x+ 的哪些性质?
提示 (1)定义域:∵x≠0,
(5)最大值、最小值:由函数的值域可知,函数无最大、最小值,但是当x>0时,函数有最小值为2,当x<0时,函数有最大值为-2.
(6)对称性:由函数的奇偶性可知,函数图象关于(0,0)成中心对称.
探究函数f(x)=x+ (a>0)的性质,并画出它的简图(单调性需证明,
其余性质列出即可).
例2
(1)定义域:{x|x≠0};
(3)奇偶性:奇函数;
所以x1-x2<0,0
即f(x1)>f(x2).
因为x1-x2<0,x1x2>a,
所以f(x1)-f(x2)<0,所以f(x1)
延伸探究 当a<0时,探究该函数的性质,并画出函数的简图(单调性需证明,其余性质列出即可).
(1)定义域:{x|x≠0};
(2)值域:R;
(3)奇偶性:奇函数;
(4)函数f(x)在区间(-∞,0),(0,+∞)上单调递增,证明如下:
任取x1,x2∈(0,+∞),且x1
即f(x1)
同理可知,函数f(x)在区间(-∞,0)上单调递增.
其简图如图所示.
(1)x∈[1,3],f(x)的最小值是____;
跟踪训练2
2
∵f(x)在[1,3]上单调递增,∴f(x)的最小值为f(1)=2.
∴最小值为f(1)=2,
对勾函数的综合运用
三
问题7 应用基本不等式求最值应注意哪些?
提示 一正,二定,三相等.
(1)当a=4时,求函数f(x)在x∈(0,+∞)上的最小值;
例3
∴f(x)的最小值为2.
(2)当a>0时,求函数f(x)在[2,+∞)上的最小值.
∴f(x1)-f(x2)>0,即f(x1)>f(x2),
设f(x)的最小值为g(a),
求对勾函数的最值问题,可以利用函数的单调性研究,也可以利用基本不等式.
反思感悟
(1)已知x>0,求y= 的最大值,并求此时x的值.
跟踪训练3
(2)已知x≥2,求y=x+ 的最小值(提示:利用图象助解).
课堂
小结
1.知识清单:
(1)反比例函数的图象和性质.
(2)对勾函数的图象和性质.
2.方法归纳:分类讨论、数形结合.
3.常见误区:研究函数的性质一定先确定函数的定义域.
随堂演练
1.函数y= ,当x>0时,y随x的增大而增大,那么m的取值范围是
A.m<3 B.m>3
C.m<-3 D.m>-3
√
1
2
3
4
在反比例函数y= 中,若k>0,在x>0时,y随x的增大而减小,若k<0,
在x>0时,y随x的增大而增大,所以由题意得m-3<0,m<3.
1
2
3
4
2.(多选)已知函数y= ,下列结论中正确的是
A.其图象经过点(3,1)
B.其图象分别位于第一、三象限
C.当x>0时,y随x的增大而减小
D.当x>1时,y>3
√
√
√
1
2
3
4
反比例函数y= ,当x=3时,y=1,故A正确;
因为y= 分子大于0,所以图象在第一、三象限,故B正确;
反比例函数在第一、三象限上都单调递减,所以C正确;
因为在(0,+∞) 上,y= 单调递减,所以当x>1时,0
2
3
4
3.已知点P(a,m),Q(b,n)都在函数 的图象上,且a<0<b,则下列结论一定正确的是
A.m+n<0 B.m+n>0
C.m>n D.m<n
√
1
2
3
4
∵a<0,
∴P(a,m)在第二象限,
∴m>0.
∵b>0,
∴Q(b,n)在第四象限,
∴n<0.
∴n<0<m,即m>n.
1
2
3
4
(0,2)
1
2
3
4
∴实数t的取值范围为(0,2).
课时对点练
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
A.A=B B.A=C
C.B=C D.A=B=C
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2. 某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(千帕)是气球体积V(立方米)的反比例函数,其图象如图所示,则这个函数的解析式为
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.函数f(x)=x+ 在区间[1,3]上的最大值是
A.3 B.5 C.4 D.
√
由对勾函数的图象的特点可知,x=2时函数有最小值,x=1时,函数有最大值为5.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.函数f(x)=x+ (a>0,x∈R,x≠0)的奇偶性为
A.奇函数 B.偶函数
C.非奇非偶函数 D.无法判断
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.函数g(x)=x+ 的单调递减区间为
A.(-2,0)∪(0,2) B.(-2,2)
C.(-2,0)和(0,2) D.(-∞,-2)和(2,+∞)
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
则函数在区间(1,+∞)上单调递减.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
再向上平移1个单位长度得到的,
∴对称中心为(-1,1).
(-1,1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.在平面直角坐标系中,函数y=-x+a与函数y= 的图象有两个公共点,
则实数a的取值范围是 ____________.
a<-2或a>2
函数y=-x+a与反比例函数y= 的图象有两个公共点,
则方程组有两个解,即方程①有两个不同的解,
Δ=a2-4>0,a<-2或a>2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.作出函数y= 的图象,并写出函数的单调区间和值域.
函数在(-∞,2)和(2,+∞)上单调递减.
故单调递减区间为(-∞,2)和(2,+∞),无单调递增区间.值域为(-∞,1)∪(1,+∞).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.一家货物公司计划租地建造仓库储存货物,经过市场调查了解到下列信息:每月土地占地费y1(单位:万元)与仓库到车站的距离x(单位:km)成反比,每月库存货物费y2(单位:万元)与(4x+1)成正比;若在距离车站10 km处建仓库,则y1与y2分别为2万元和8.2万元.记两项费用之和为w.
(1)求w关于x的解析式;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∵每月土地占地费y1(单位:万元)与仓库到车站的距离x(单位:km)成反比,
∵每月库存货物费y2(单位:万元)与(4x+1)成正比,
∴可设y2=(4x+1)k2,
又∵在距离车站10 km处建仓库,则y1与y2分别为2万元和8.2万元,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)这家公司应该把仓库建在距离车站多少千米处,才能使两项费用之和最小?求出最小值.
∴这家公司应该把仓库建在距离车站5千米处,才能使两项费用之和最小,最小值为8.2万元.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
11.函数f(x)= (x∈R)的值域是
A.(0,1) B.(0,1]
C.[0,1) D.[0,1]
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∵x<0,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.一批救灾物资随26辆汽车从某市以v km/h的速度送达灾区,已知运送的路线长400 km,为了安全起见,两辆汽车的间距不得小于 ,那么这批物资全部到达灾区最少需要
A.5 h B.10 h C.15 h D.20 h
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
设这批物资全部到达灾区的时间为t h,
故这批物资全部到达灾区最少需要10 h.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.函数f(x)=x- 的单调递增区间为_____________________.
画出函数图象如图,可知函数f(x)的单调递增区间为(-∞,0)和(0,+∞).
(-∞,0)和(0,+∞)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
15.已知函数f(x)= 若存在0
(96,100)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
可得函数图象如图所示.
由图可知,当y∈(4,5)时,存在0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴x1x2x3x4=4x3x4=4x3(10-x3)=-4(x3-5)2+100,
其中x3∈(4,5),则-4(x3-5)2+100∈(96,100),
即x1x2x3x4∈(96,100).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为x∈[0,1],则t=2x+1∈[1,3].
由已知性质可知u(t)在[1,2]上单调递减,在[2,3]上单调递增.
所以f(x)max=-3,所以值域为[-4,-3].
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)对于(1)中的函数f(x)和函数g(x)=-x-2a,若对任意x1∈[0,1],总存在x2∈[0,1],使得g(x2)=f(x1)成立,求实数a的值.
因为g(x)=-x-2a为减函数,所以当x∈[0,1]时,g(x)∈[-1-2a,-2a].
因为对任意x1∈[0,1],总存在x2∈[0,1],使得g(x2)=f(x1)成立,
所以f(x)的值域是g(x)值域的子集,
本课结束
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
