西师大版数学六年级上册4.2 比的基本性质 课件(24张ppt)
文档属性
| 名称 | 西师大版数学六年级上册4.2 比的基本性质 课件(24张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-27 13:04:27 | ||
图片预览






文档简介
(共24张PPT)
第2课时 比的基本性质
比和按比例分配
义务教育西师大版六年级上册
四
复习导入
什么叫比?
两个数相除又叫做两个数的比。
16÷25
商不变的性质∶在除法里,被除数和除数同时乘(或除以)一个相同的数(0除外),商不变。
=(16×4)÷(25 × 4)
=64 ÷ 100
=0.64
30÷10
=(30÷10)÷(10÷10)
=3÷1
=3
计算∶
分数的基本性质∶分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。
通分∶
和
把下列分数约成最简分数∶
探究新知
2
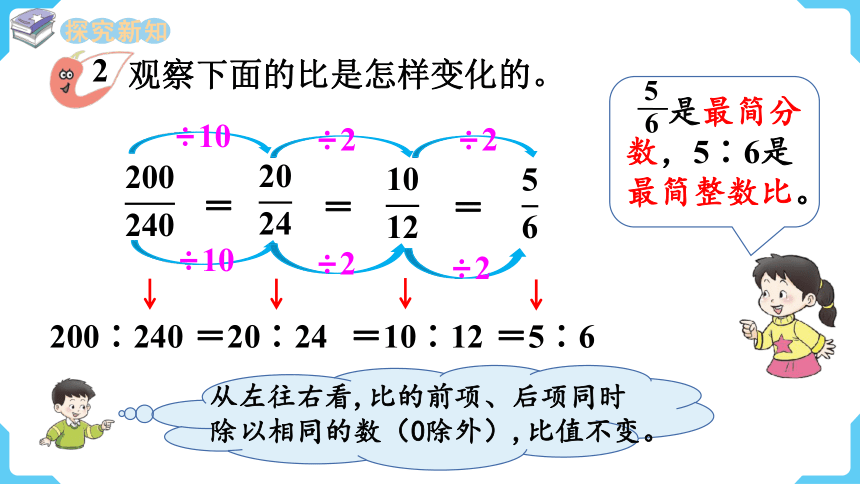
观察下面的比是怎样变化的。
200∶240
=
=
=
=20∶24
=10∶12
=5∶6
÷10
÷10
÷2
÷2
÷2
÷2
从左往右看,比的前项、后项同时除以相同的数(0除外),比值不变。
是最简分数,5∶6是最简整数比。
5
6
2
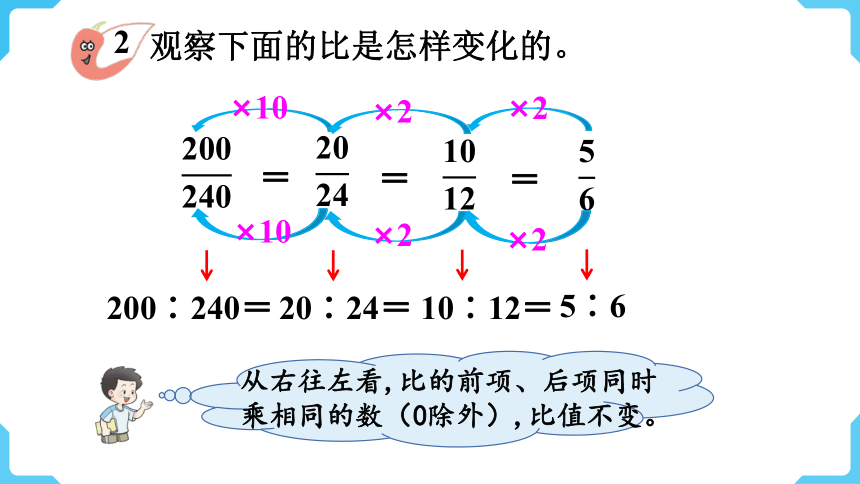
观察下面的比是怎样变化的。
200∶240=
=
=
=
20∶24=
10∶12=
5∶6
×10
×10
×2
×2
×2
×2
从右往左看,比的前项、后项同时乘相同的数(0除外),比值不变。
比的前项和后项同时乘或除以相同的数
(0除外),比值不变。这叫做比的基本性质。
比的基本性质
3
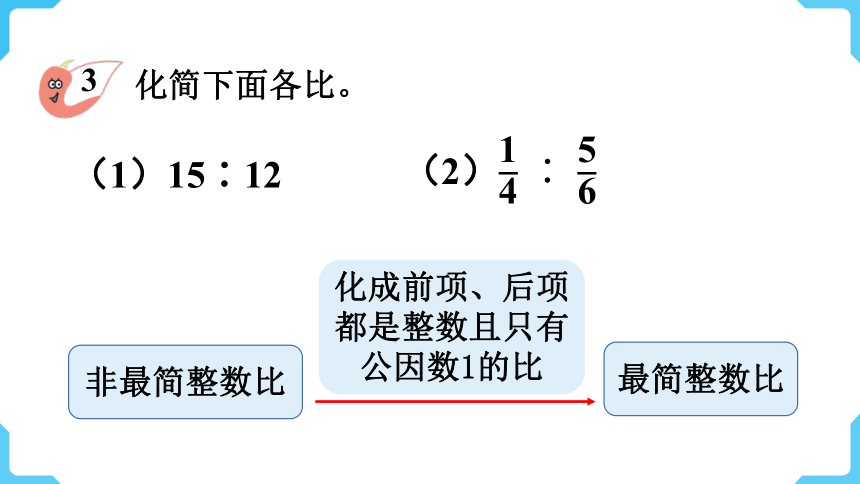
化简下面各比。
(1)15∶12
(2)
非最简整数比
最简整数比
化成前项、后项都是整数且只有公因数1的比
3
化简下面各比。
(1)15∶12
方法一∶
15∶12
=
=
=
5∶4
方法二∶15∶12 = ( 15÷3 )∶( 12÷3 ) = 5∶4
为什么要同时除以 3?
比较简便!
化简整数比的方法∶用比的前项、后项分别除以它们的最大公约数。
(2)
方法一∶
方法二∶
∶
=
=
=
=3∶10
= (
=3∶10
比较简便!
比的前、后项都乘它们的分母的最小公倍数,就可以把分数比转化为整数比,进而化简成为最简整数比。
把下面的比化成最简整数比。
200∶4
200∶4=(200÷4)∶(4÷4)=50 ∶1
试一试
1.8∶2.7
1.8∶2.7
= (1.8×10)∶(2.7×10)= 18∶27
把下面的比化成最简整数比。
200∶4
1.8∶2.7
1.议一议。
比的基本性质和商不变的性质,分数的基本性质
有什么联系?
比的基本性质、分数的基本性质和除法商不变的性质在本质上是同一个规律。
课桌椅型号 标准身高 学生身高范围 桌面高 座面高
5号 150.0 143-157 64 36
6号 142.5 135-149 61 34
7号 135.0 128-142 58 32
《学校课桌椅功能尺寸》(部分)
国家标准(GB/T3976-2002)单位∶cm
中小学校课桌椅的型号
2.阅读下面的资料,说出两个量的比,并把能化简的比化简。
课桌椅型号 标准身高 学生身高范围 桌面高 座面高
5号 150.0 143-157 64 36
6号 142.5 135-149 61 34
7号 135.0 128-142 58 32
中小学校课桌椅的型号
5号课桌椅的座面高与6号课桌椅的座面高的比是36∶34
36∶34 = 18∶17
(答案不唯一)
应届高中毕业生人数与高校计划招生人数∶
800∶680=(800÷40)∶(680÷40)= 20∶17
1. 2011年全国高考人数情况如下表∶
写出某两个量的比,并化简。
课堂练习
教材第52页“练习十四”第3题
(答案不唯一)
6∶10
12∶21
2.化简下面各比。
教材第53页“练习十四”第4题
6∶10
12∶21
48
32
2
5
∶
1
4
48
32
=48∶32
2
5
∶
1
4
=( ×20)∶( ×20)
2
5
1
4
= 8∶5
= 3∶5
=(6÷2)∶(10÷2)
=4∶7
=(12÷3)∶(21÷3)
=3∶2
=(48÷16)∶(32÷16)
0.4∶0.6
0.4∶0.6
1
20
∶
1
4
1
20
∶
1
4
=( ×20)∶( ×20)
1
20
1
4
= 1∶5
= 4∶6
=(0.4×10)∶(0.6×10)
0.25∶1
3
4
∶
2
= 2∶3
0.25∶1
= 25 ∶100
=(0.25×100)∶(1×100)
= 1∶4
3
4
∶
2
=( ×4)∶( ×4)
3
4
2
= 3∶8
甲∶乙∶丙=2∶3∶4
甲∶丙
3.甲数和乙数的比是2∶3,乙数和丙数的比是
3∶4,甲、丙两个数的比是多少?
教材第53页“练习十四”第6题
=1∶2
=2∶4
答:甲、丙两个数的比是1∶2。
3600÷5=720(双)
720×(9-5)= 2880(双)
答∶下半年皮鞋的产量是2880双。
4.皮鞋厂上半年皮鞋的产量与全年皮鞋的总产量比是 ,上半年皮鞋的产量是3600双。下半年皮鞋的产量是多少双?
教材第53页“练习十四”第9题
5
9
把重叠部分的面积看作单位“1”,则大长方形的面积为1÷ =6,小长方形的面积为1÷ =4,所以这两个长方形的面积的比是6∶4=3∶2。
两个长方形重叠部分的面积,相当于大长方形面积的 ,相当于小长方形面积的 。这两个长方形的面积的比是多少?
思考题
教材第53页“练习十四”思考题
1
6
1
4
通过这节课的学习活动,你有什么收获?
课堂小结
比的前项和后项同时乘或除以相同的数(0除外),比值不变。这就是比的基本性质。
把比化成最简整数比的过程,叫做化简比。
化简比的结果应是最简整数比。
1.完成课本练习十四2.5题。
课后作业
谢谢!
第2课时 比的基本性质
比和按比例分配
义务教育西师大版六年级上册
四
复习导入
什么叫比?
两个数相除又叫做两个数的比。
16÷25
商不变的性质∶在除法里,被除数和除数同时乘(或除以)一个相同的数(0除外),商不变。
=(16×4)÷(25 × 4)
=64 ÷ 100
=0.64
30÷10
=(30÷10)÷(10÷10)
=3÷1
=3
计算∶
分数的基本性质∶分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。
通分∶
和
把下列分数约成最简分数∶
探究新知
2
观察下面的比是怎样变化的。
200∶240
=
=
=
=20∶24
=10∶12
=5∶6
÷10
÷10
÷2
÷2
÷2
÷2
从左往右看,比的前项、后项同时除以相同的数(0除外),比值不变。
是最简分数,5∶6是最简整数比。
5
6
2
观察下面的比是怎样变化的。
200∶240=
=
=
=
20∶24=
10∶12=
5∶6
×10
×10
×2
×2
×2
×2
从右往左看,比的前项、后项同时乘相同的数(0除外),比值不变。
比的前项和后项同时乘或除以相同的数
(0除外),比值不变。这叫做比的基本性质。
比的基本性质
3
化简下面各比。
(1)15∶12
(2)
非最简整数比
最简整数比
化成前项、后项都是整数且只有公因数1的比
3
化简下面各比。
(1)15∶12
方法一∶
15∶12
=
=
=
5∶4
方法二∶15∶12 = ( 15÷3 )∶( 12÷3 ) = 5∶4
为什么要同时除以 3?
比较简便!
化简整数比的方法∶用比的前项、后项分别除以它们的最大公约数。
(2)
方法一∶
方法二∶
∶
=
=
=
=3∶10
= (
=3∶10
比较简便!
比的前、后项都乘它们的分母的最小公倍数,就可以把分数比转化为整数比,进而化简成为最简整数比。
把下面的比化成最简整数比。
200∶4
200∶4=(200÷4)∶(4÷4)=50 ∶1
试一试
1.8∶2.7
1.8∶2.7
= (1.8×10)∶(2.7×10)= 18∶27
把下面的比化成最简整数比。
200∶4
1.8∶2.7
1.议一议。
比的基本性质和商不变的性质,分数的基本性质
有什么联系?
比的基本性质、分数的基本性质和除法商不变的性质在本质上是同一个规律。
课桌椅型号 标准身高 学生身高范围 桌面高 座面高
5号 150.0 143-157 64 36
6号 142.5 135-149 61 34
7号 135.0 128-142 58 32
《学校课桌椅功能尺寸》(部分)
国家标准(GB/T3976-2002)单位∶cm
中小学校课桌椅的型号
2.阅读下面的资料,说出两个量的比,并把能化简的比化简。
课桌椅型号 标准身高 学生身高范围 桌面高 座面高
5号 150.0 143-157 64 36
6号 142.5 135-149 61 34
7号 135.0 128-142 58 32
中小学校课桌椅的型号
5号课桌椅的座面高与6号课桌椅的座面高的比是36∶34
36∶34 = 18∶17
(答案不唯一)
应届高中毕业生人数与高校计划招生人数∶
800∶680=(800÷40)∶(680÷40)= 20∶17
1. 2011年全国高考人数情况如下表∶
写出某两个量的比,并化简。
课堂练习
教材第52页“练习十四”第3题
(答案不唯一)
6∶10
12∶21
2.化简下面各比。
教材第53页“练习十四”第4题
6∶10
12∶21
48
32
2
5
∶
1
4
48
32
=48∶32
2
5
∶
1
4
=( ×20)∶( ×20)
2
5
1
4
= 8∶5
= 3∶5
=(6÷2)∶(10÷2)
=4∶7
=(12÷3)∶(21÷3)
=3∶2
=(48÷16)∶(32÷16)
0.4∶0.6
0.4∶0.6
1
20
∶
1
4
1
20
∶
1
4
=( ×20)∶( ×20)
1
20
1
4
= 1∶5
= 4∶6
=(0.4×10)∶(0.6×10)
0.25∶1
3
4
∶
2
= 2∶3
0.25∶1
= 25 ∶100
=(0.25×100)∶(1×100)
= 1∶4
3
4
∶
2
=( ×4)∶( ×4)
3
4
2
= 3∶8
甲∶乙∶丙=2∶3∶4
甲∶丙
3.甲数和乙数的比是2∶3,乙数和丙数的比是
3∶4,甲、丙两个数的比是多少?
教材第53页“练习十四”第6题
=1∶2
=2∶4
答:甲、丙两个数的比是1∶2。
3600÷5=720(双)
720×(9-5)= 2880(双)
答∶下半年皮鞋的产量是2880双。
4.皮鞋厂上半年皮鞋的产量与全年皮鞋的总产量比是 ,上半年皮鞋的产量是3600双。下半年皮鞋的产量是多少双?
教材第53页“练习十四”第9题
5
9
把重叠部分的面积看作单位“1”,则大长方形的面积为1÷ =6,小长方形的面积为1÷ =4,所以这两个长方形的面积的比是6∶4=3∶2。
两个长方形重叠部分的面积,相当于大长方形面积的 ,相当于小长方形面积的 。这两个长方形的面积的比是多少?
思考题
教材第53页“练习十四”思考题
1
6
1
4
通过这节课的学习活动,你有什么收获?
课堂小结
比的前项和后项同时乘或除以相同的数(0除外),比值不变。这就是比的基本性质。
把比化成最简整数比的过程,叫做化简比。
化简比的结果应是最简整数比。
1.完成课本练习十四2.5题。
课后作业
谢谢!
