华东师大版八年级数学上册 12.1幂的运算(第3课时积的乘方)教学课件(共19张PPT)
文档属性
| 名称 | 华东师大版八年级数学上册 12.1幂的运算(第3课时积的乘方)教学课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-27 15:16:09 | ||
图片预览





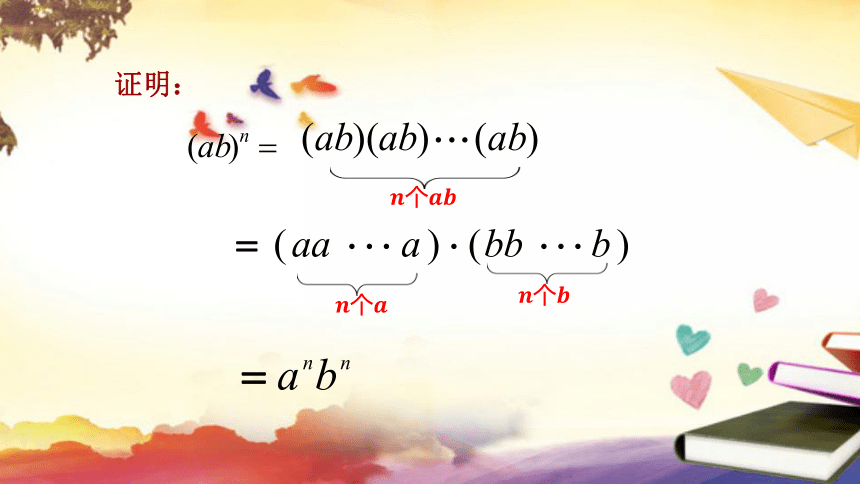

文档简介
(共19张PPT)
第 12 章 整式的乘除
12.1 幂的运算
第3课时 积的乘方
学习目标
1
2
经历探索积的乘方运算性质的过程,理解并掌握积的乘方法则.(重点)
会运用积的乘方法则进行运算.(难点)
复习回顾
填空:
1. =_____,依据________________.
2. =____,依据_________________ _.
3.(4)3=_____,依据___________________.
合并同类项法则
同底数幂乘法的运算性质
12
幂的乘方的运算性质
计算
22×32
=4×9
=36
(2×3)2
=(2×3)(2×3)
=6×6=36
你能发现什么
22×32
= (2×3)2
()2与2是否相等
新课导入
知识讲解
问题:填空,看看运算过程用到哪些运算律,从运算结果看能发现什么规律?
猜想:积的乘方(ab)n = anbn (n为正整数)
(1)()2=()·()=(·)·(·)
=( )( )
(2)()3=_______________
=___________
=( )( )
2
2
()·( )·( )
()·()
3
3
(乘方的意义)
(乘法交换律、结合律)
(同底数幂相乘的法则)
证明:
个
个
个
语言表述:
积的乘方法则
积的乘方,等于把积的每一个因式分别_____,再把所得的幂________.
(ab)n = anbn (n为正整数)
乘方
相乘
计算:
(1)(2b)3 ; (2)(2a3)2 ; (3)(-a)3; (4)(-3x)4 .
=23b3
= 8b3
(1) (2b)3
解:
(2) (2a3)2
= 22×(a3)2
= 4a6
(3) (-a)3
= (-1)3 ·a3
= -a3
(4) (-3x)4
= (-3)4 · x4
= 81x4
例1
注意:运用积的乘方法则进行计算时,注意每个因式都要乘方,尤其是字母的系数不要漏乘方.
计算:
(1) (2a)3 ; (2) b)3 ;
(3) (xy2)2 ; (4) x3)4.
解:(1)原式=
(2)原式=
(3)原式=
(4)原式=
.
=.
=x2y4.
=16x12.
)3·b3
x2·(y2)2
)4·(x3)4
巩固练习
想一想:1.三个或三个以上因式的积的乘方等于什么?
(abc)n = anbncn (n为正整数)
积的乘方公式的推广
2.积的乘方法则的逆用:
anbn = (ab)n (n为正整数)
课题提升
1.计算:
(1) 3 · 4· +(2)4+(4)2;
(2) 2(3)2 · 3(33)3+(5)2 · 7 .
解: (1)原式= 3+4+1+ 2×4+(2)2 · (4)2
(2)原式=26 · 3279+252 · 7
注意:运算顺序是先乘方,再乘除,最后算加减.
= 8+ 8+4 8
=6 8 ;
=29279+259
=0.
2.
计算:(0.04)100×[(-5)100]2
=(0.22)100 × 5200
=(0.2)200 × 5200
=(0.2×5)200
=1200
(0.04)100×[(-5)100]2
=1.
解法一:
=(0.04)100× [(-5)2]100
=(0.04×25)100
=1100
=1.
= (0.04)100 ×(25)100
(0.04)100×[(-5)100]2
解法二:
随堂训练
1.
下列各式中正确的有几个?( )
A.1个 B.2个 C.3个 D.4个
C
(1)(2)3=6 ( )
×
×
×
(2) (3)3=93 ( )
×
(3) 2)2( )
(4) 2)2= ( )
2.判断:
√
( )
)
)
7
(
)
5
(
-
-
1
7
3
3
7
(
)
7
3
(
3
5
5
5
=
-
=
(
-
×
计算:
(1)(223)3 ;
(2) (332)4 .
3.
解:(1)原式=(·(2)3 ·(3)3
(2)原式=(3)4 ·(3)4 ·(2)4 · 4
=69 ;
= 81 1284 .
4.地球可以近似地看做是球体,如果用分别代表球的体积和半径,那么 。 地球的半径约为6×103 km,它的体积大约是多少
解:
=
×(6×103)3
=
×
63×109
≈
9.05×1011
(km3)
5.如果(an·bm)3=a9b15,求m,n的值.
(an)3·(bm)3=a9b15,
a3n ·b3m=a9b15 ,
3n=9 ,3m=15,
n=3,m=5.
解:∵(an·bm)3=a9b15,
课堂小结
1、积的乘方法则
语言表述:
积的乘方,等于把积的每一个因式分别_____,再把所得的幂________.
(ab)n = anbn (n为正整数)
乘方
相乘
(abc)n = anbncn (n为正整数)
2.积的乘方公式的推广
3.积的乘方法则的逆用
anbn = (ab)n (n为正整数)
第 12 章 整式的乘除
12.1 幂的运算
第3课时 积的乘方
学习目标
1
2
经历探索积的乘方运算性质的过程,理解并掌握积的乘方法则.(重点)
会运用积的乘方法则进行运算.(难点)
复习回顾
填空:
1. =_____,依据________________.
2. =____,依据_________________ _.
3.(4)3=_____,依据___________________.
合并同类项法则
同底数幂乘法的运算性质
12
幂的乘方的运算性质
计算
22×32
=4×9
=36
(2×3)2
=(2×3)(2×3)
=6×6=36
你能发现什么
22×32
= (2×3)2
()2与2是否相等
新课导入
知识讲解
问题:填空,看看运算过程用到哪些运算律,从运算结果看能发现什么规律?
猜想:积的乘方(ab)n = anbn (n为正整数)
(1)()2=()·()=(·)·(·)
=( )( )
(2)()3=_______________
=___________
=( )( )
2
2
()·( )·( )
()·()
3
3
(乘方的意义)
(乘法交换律、结合律)
(同底数幂相乘的法则)
证明:
个
个
个
语言表述:
积的乘方法则
积的乘方,等于把积的每一个因式分别_____,再把所得的幂________.
(ab)n = anbn (n为正整数)
乘方
相乘
计算:
(1)(2b)3 ; (2)(2a3)2 ; (3)(-a)3; (4)(-3x)4 .
=23b3
= 8b3
(1) (2b)3
解:
(2) (2a3)2
= 22×(a3)2
= 4a6
(3) (-a)3
= (-1)3 ·a3
= -a3
(4) (-3x)4
= (-3)4 · x4
= 81x4
例1
注意:运用积的乘方法则进行计算时,注意每个因式都要乘方,尤其是字母的系数不要漏乘方.
计算:
(1) (2a)3 ; (2) b)3 ;
(3) (xy2)2 ; (4) x3)4.
解:(1)原式=
(2)原式=
(3)原式=
(4)原式=
.
=.
=x2y4.
=16x12.
)3·b3
x2·(y2)2
)4·(x3)4
巩固练习
想一想:1.三个或三个以上因式的积的乘方等于什么?
(abc)n = anbncn (n为正整数)
积的乘方公式的推广
2.积的乘方法则的逆用:
anbn = (ab)n (n为正整数)
课题提升
1.计算:
(1) 3 · 4· +(2)4+(4)2;
(2) 2(3)2 · 3(33)3+(5)2 · 7 .
解: (1)原式= 3+4+1+ 2×4+(2)2 · (4)2
(2)原式=26 · 3279+252 · 7
注意:运算顺序是先乘方,再乘除,最后算加减.
= 8+ 8+4 8
=6 8 ;
=29279+259
=0.
2.
计算:(0.04)100×[(-5)100]2
=(0.22)100 × 5200
=(0.2)200 × 5200
=(0.2×5)200
=1200
(0.04)100×[(-5)100]2
=1.
解法一:
=(0.04)100× [(-5)2]100
=(0.04×25)100
=1100
=1.
= (0.04)100 ×(25)100
(0.04)100×[(-5)100]2
解法二:
随堂训练
1.
下列各式中正确的有几个?( )
A.1个 B.2个 C.3个 D.4个
C
(1)(2)3=6 ( )
×
×
×
(2) (3)3=93 ( )
×
(3) 2)2( )
(4) 2)2= ( )
2.判断:
√
( )
)
)
7
(
)
5
(
-
-
1
7
3
3
7
(
)
7
3
(
3
5
5
5
=
-
=
(
-
×
计算:
(1)(223)3 ;
(2) (332)4 .
3.
解:(1)原式=(·(2)3 ·(3)3
(2)原式=(3)4 ·(3)4 ·(2)4 · 4
=69 ;
= 81 1284 .
4.地球可以近似地看做是球体,如果用分别代表球的体积和半径,那么 。 地球的半径约为6×103 km,它的体积大约是多少
解:
=
×(6×103)3
=
×
63×109
≈
9.05×1011
(km3)
5.如果(an·bm)3=a9b15,求m,n的值.
(an)3·(bm)3=a9b15,
a3n ·b3m=a9b15 ,
3n=9 ,3m=15,
n=3,m=5.
解:∵(an·bm)3=a9b15,
课堂小结
1、积的乘方法则
语言表述:
积的乘方,等于把积的每一个因式分别_____,再把所得的幂________.
(ab)n = anbn (n为正整数)
乘方
相乘
(abc)n = anbncn (n为正整数)
2.积的乘方公式的推广
3.积的乘方法则的逆用
anbn = (ab)n (n为正整数)
