2022-2023学年人教A版2019高中数学 必修1 §1.4.1 充分条件与必要条件 课件(48张PPT)
文档属性
| 名称 | 2022-2023学年人教A版2019高中数学 必修1 §1.4.1 充分条件与必要条件 课件(48张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-27 14:39:32 | ||
图片预览











文档简介
(共48张PPT)
1.4.1 充分条件与必要条件
第一章 §1.4 充分条件与必要条件
学习目标
1.理解充分条件、必要条件的概念.
2.了解充分条件与判定定理,必要条件与性质定理的关系.
3.能通过充分性、必要性解决简单的问题.
导语
不知道大家有没有这样的经历,在初中的某次考试没有考好,父母就着急了,说:“初中不好好学习就考不上高中,考不上高中就考不上大学,考不上大学就找不到工作,找不到工作就实现不了自己的人生价值……那么,你这一辈子就完了!”大家同意这么糟糕的说法吗?静下心来想想,一次没有考好,跟后面这些事情有关系吗?把几乎没有关系的两件事情理解成了充分条件,让你们的父母徒增烦恼,当然你们也有了不小的压力,所以,大家要好好学习这节课,这样你就能解决你父母的烦恼了!
一、充分条件与必要条件
二、充分条件与必要条件的应用
课时对点练
随堂演练
内容索引
充分条件与必要条件
一
问题 观察下面几个命题,你能把它们变成“若p,则q”的形式吗?你能得到什么?
(1)两组对边分别相等的四边形是平行四边形;
提示 若四边形的两组对边分别相等,则这个四边形是平行四边形.
(2)一组对边平行且相等的四边形是平行四边形;
提示 若四边形的一组对边平行且相等,则这个四边形是平行四边形.
(3)两条对角线互相平分的四边形是平行四边形;
提示 若四边形的两条对角线互相平分,则这个四边形是平行四边形.
(4)平行四边形的两组对边分别相等;
提示 若四边形是平行四边形,则四边形的两组对边分别相等.
(5)平行四边形的一组对边平行且相等;
提示 若四边形是平行四边形,则四边形的一组对边平行且相等.
(6)平行四边形的两条对角线互相平分.
提示 若四边形是平行四边形,则四边形的两条对角线互相平分.
由此可见,数学中的每一条判定定理都给出了相应数学结论成立的一个充分条件,即使结论成立的条件并不唯一.数学中的每一条性质定理都给出了相应数学结论成立的一个必要条件,即所获得的结论也不唯一.
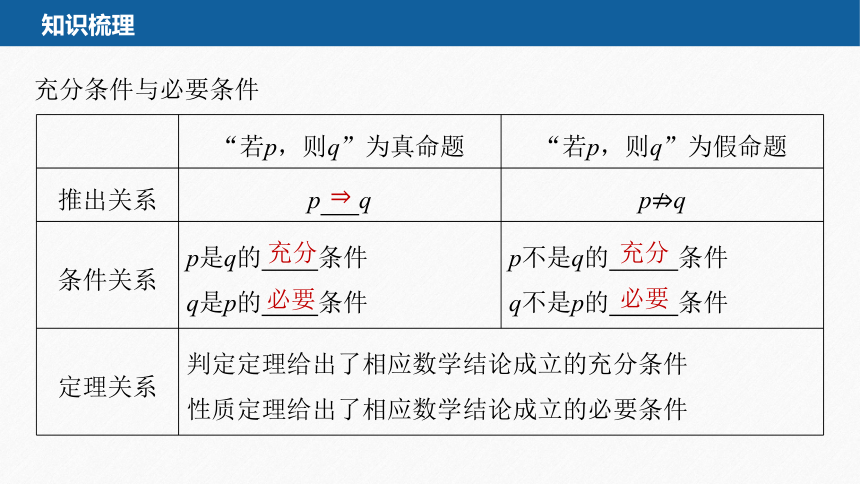
知识梳理
充分条件与必要条件
“若p,则q”为真命题 “若p,则q”为假命题
推出关系 p q p q
条件关系 p是q的 条件 q是p的 条件 p不是q的 条件
q不是p的 条件
定理关系 判定定理给出了相应数学结论成立的充分条件 性质定理给出了相应数学结论成立的必要条件
充分
必要
充分
必要
(1)前提p q,有方向,条件在前,结论在后.
(2)若p q,则p是q的充分条件或q是p的必要条件.
(3)“p是q的充分条件”,“q是p的必要条件”,“q的一个充分条件是p”,“p的一个必要条件是q”,说的是同一个意思.
注意点:
(1)指出下列哪些命题中p是q的充分条件?
①在△ABC中,p:∠B>∠C,q:AC>AB;
例1
在△ABC中,由大角对大边知,∠B>∠C AC>AB,所以p是q的充分条件.
②已知x,y∈R,p:x=1,q:(x-1)(x-2)=0;
由x=1 (x-1)(x-2)=0,故p是q的充分条件.
③已知x∈R,p:x>1,q:x>2.
方法一 由x>1 x>2,所以p不是q的充分条件.
方法二 设集合A={x|x>1},B={x|x>2},
所以B A,所以p不是q的充分条件.
(2)指出下列哪些命题中q是p的必要条件?
①p:一个四边形是矩形,q:四边形的对角线相等;
因为矩形的对角线相等,所以q是p的必要条件.
②p:A B,q:A∩B=A;
因为p q,
所以q是p的必要条件.
③p:a>b,q:ac>bc.
因为p q,
所以q不是p的必要条件.
充分、必要条件的判断方法
(1)判断p是q的什么条件,主要判断若p成立时,能否推出q成立,反过来,若q成立时,能否推出p成立;若p q为真,则p是q的充分条件,若q p为真,则p是q的必要条件.
(2)也可利用集合的关系判断,如果条件甲“x∈A”,条件乙“x∈B”.若A B,则甲是乙的必要条件.
反思感悟
跟踪训练1
分析下列各项中p与q的关系.
(1)p:α为锐角,q:α=45°.
由于q p,p q,故p是q的必要条件,q是p的充分条件.
(2)p:(x+1)(x-2)=0,q:x+1=0.
由于q p,p q,故p是q的必要条件,q是p的充分条件.
充分条件与必要条件的应用
二
已知集合P={x|-2<x<4},Q={x|3m-2≤x≤5m+2,m∈R}.若P的充分条件为Q,求实数m的取值范围.
例2
由已知,P的充分条件为Q,则Q是P的子集.
当3m-2>5m+2,即m<-2时,Q= ,满足题意,
当3m-2≤5m+2,即m≥-2时,
延伸探究 已知集合P={x|-2<x<1},Q={x|3m-2≤x≤5m+2,m∈R}.若P的必要条件为Q,求实数m的取值范围.
由题意得,P是Q的子集,
充分条件与必要条件的应用技巧
(1)应用:可利用充分性与必要性进行相关问题的求解,特别是求参数的值或取值范围问题.
(2)求解步骤:先把p,q等价转化,利用充分条件、必要条件与集合间的包含关系,建立关于参数的不等式(组)进行求解.
反思感悟
已知P={x|a-4跟踪训练2
因为“x∈P”是“x∈Q”的必要条件,
所以Q P,
-1≤a≤5
课堂
小结
1.知识清单:
(1)充分条件、必要条件的概念.
(2)充分条件与判定定理,必要条件与性质定理的关系.
(3)充分条件、必要条件的判断.
(4)充分条件与必要条件的应用.
2.方法归纳:等价转化.
3.常见误区:充分条件、必要条件不唯一;求参数范围时能否取到端点值.
随堂演练
1.若p是q的充分条件,则q是p的
A.充分条件
B.必要条件
C.既不是充分条件也不是必要条件
D.既是充分条件又是必要条件
√
1
2
3
4
因为p是q的充分条件,所以p q,
所以q是p的必要条件.
2.“四边形的四条边相等”是“四边形是正方形”的
A.充分条件
B.必要条件
C.既是充分条件又是必要条件
D.既不是充分条件也不是必要条件
√
1
2
3
4
因为正方形的四条边相等,但四条边相等的四边形不一定是正方形,所以“四边形的四条边相等”是“四边形是正方形”的必要条件.
3.使x>3成立的一个充分条件是
A.x>4 B.x>0
C.x>2 D.x<2
√
1
2
3
4
只有x>4 x>3,其他选项均不可推出x>3.
4.若“x>1”是“x>a”的充分条件,则a的取值范围是______.
1
2
3
4
a≤1
因为x>1 x>a,所以a≤1.
课时对点练
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
1.下列命题中,p是q的充分条件的是
A.p:ab≠0,q:a≠0
B.p:a2+b2≥0,q:a≥0且b≥0
C.p:x2>1,q:x>1
根据充分条件的概念逐一判断,
只有ab≠0 a≠0.
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2.使x>1成立的一个必要条件是
A.x>0 B.x>3 C.x>2 D.x<2
√
只有x>1 x>0,其他选项均不可由x>1推出.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.已知集合A={3,m},B={1,3,5},则m=1是A B的
A.充分条件 B.必要条件
C.既不是充分条件也不是必要条件 D.既是充分条件又是必要条件
√
若A B,则有m∈B且m≠3,所以m=1或m=5,故当m=1时,有A B,而A B时,m不一定是1,故m=1是A B的充分条件,不是必要条件.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.下列“若p,则q”形式的命题中,满足p是q的充分条件的是
A.若平面内点P在线段AB的垂直平分线上,则PA=PB
B.若x是无理数,则x2也是无理数
C.若x>y,则x2>y2
D.若x2>y2,则x>y
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
线段垂直平分线上的点到两个端点的距离相等,故A正确;
若x= ,则x2=2,故B不成立;
若x=-1,y=-2,故C结论不成立;
若x=-2,y=1,故D结论不成立.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.(多选)下列说法不正确的是
A.“x>5”是“x>4”的充分条件
B.“xy=0”是“x=0且y=0”的充分条件
C.“-2D.x2-3x+2=0是x=1的必要条件
√
B中由xy=0不能推出x=0且y=0,故B不正确;
C中“-2√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.(多选)使ab>0成立的充分条件是
A.a>0,b>0 B.a+b>0
C.a<0,b<0 D.a>1,b>1
√
因为a>0,b>0 ab>0;a<0,b<0 ab>0;a>1,b>1 ab>0,所以选项A,C,D都是使ab>0成立的充分条件.
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.设集合A={1,2},
(1)请写出一个集合B_______________________,使“x∈A”是“x∈B”的充分条件,但“x∈A”不是“x∈B”的必要条件;
(2)请写出一个集合B_____________________,使“x∈A”是“x∈B”的必要条件,但“x∈A”不是“x∈B”的充分条件.
B={1,2,3}(答案不唯一)
B={1}(答案不唯一)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.条件p:2-x>0,条件q:xp:x<2,若p是q的充分条件,则p q,即p对应集合是q对应集合的子集,故a≥2.
{a|a≥2}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.指出下列命题中,p是q的什么条件?
(2)p:a2+b2=0,q:a+b=0;
∵a2+b2=0 a=b=0 a+b=0,a+b=0 a2+b2=0,∴p是q的充分条件.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(3)p:(x-1)2+(y-2)2=0,q:(x-1)(y-2)=0.
∵(x-1)2+(y-2)2=0 x=1且y=2 (x-1)(y-2)=0,
而(x-1)(y-2)=0 (x-1)2+(y-2)2=0,∴p是q的充分条件.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.已知p:-1b恒成立的实数b的取值范围.
由于p:-1又由-a依题意,得{x|-1则使a>b恒成立的实数b的取值范围是{b|b<2}.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
11.设x,y是两个实数,命题:“x,y中至少有一个数大于1”的充分条件是
A.x+y=2 B.x+y>2
C.x2+y2>2 D.xy>1
√
对于选项A,当x=1,y=1时,满足x+y=2,但命题不成立;
对于选项C,D,当x=-2,y=-3时,满足x2+y2>2,xy>1,但命题不成立,也不符合题意.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.集合A={x|-1A.{b|-2≤b<0} B.{b|0C.{b|-2√
A={x|-1因为“a=1”是“A∩B≠ ”的充分条件,
所以-1≤b-1<1或-11
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.设甲、乙、丙是三个命题,如果甲是乙的必要条件,丙是乙的充分条件,但不是乙的必要条件,那么
A.丙是甲的充分条件,但不是甲的必要条件
B.丙是甲的必要条件,但不是甲的充分条件
C.丙既是甲的充分条件,又是甲的必要条件
D.丙既不是甲的充分条件,也不是甲的必要条件
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为甲是乙的必要条件,所以乙 甲.
又因为丙是乙的充分条件,但不是乙的必要条件,所
以丙 乙,但乙 丙,如图.
综上,有丙 甲,但甲 丙,
即丙是甲的充分条件,但不是甲的必要条件.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.已知p:x<-2或x>10,q:x<1+a或x>1-a(a<0).若p是q的必要条件,则实数a的取值范围为___________.
∵p是q的必要条件,∴q p,
{a|a≤-9}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
15.“一元二次方程x2-ax+1=0有两个正实数根”的一个充分条件可以为_________________;一个必要条件可以为____________________.
因为一元二次方程x2-ax+1=0有两个正实数根,
a>3(答案不唯一)
a>-1(答案不唯一)
故一元二次方程x2-ax+1=0有两个正实数根的一个充分条件可以为a>3;
一元二次方程x2-ax+1=0有两个正实数根的一个必要条件可以为a>-1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.(1)是否存在实数m,使2x+m<0是x<-1或x>3的充分条件?
欲使2x+m<0是x<-1或x>3的充分条件,
所以m≥2.
故存在实数m≥2,使2x+m<0是x<-1或x>3的充分条件.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)是否存在实数m,使2x+m<0是x<-1或x>3的必要条件?
欲使2x+m<0是x<-1或x>3的必要条件,
则只要{x|x<-1或x>3} ,这是不可能的.
故不存在实数m,使2x+m<0是x<-1或x>3的必要条件.
本课结束
1.4.1 充分条件与必要条件
第一章 §1.4 充分条件与必要条件
学习目标
1.理解充分条件、必要条件的概念.
2.了解充分条件与判定定理,必要条件与性质定理的关系.
3.能通过充分性、必要性解决简单的问题.
导语
不知道大家有没有这样的经历,在初中的某次考试没有考好,父母就着急了,说:“初中不好好学习就考不上高中,考不上高中就考不上大学,考不上大学就找不到工作,找不到工作就实现不了自己的人生价值……那么,你这一辈子就完了!”大家同意这么糟糕的说法吗?静下心来想想,一次没有考好,跟后面这些事情有关系吗?把几乎没有关系的两件事情理解成了充分条件,让你们的父母徒增烦恼,当然你们也有了不小的压力,所以,大家要好好学习这节课,这样你就能解决你父母的烦恼了!
一、充分条件与必要条件
二、充分条件与必要条件的应用
课时对点练
随堂演练
内容索引
充分条件与必要条件
一
问题 观察下面几个命题,你能把它们变成“若p,则q”的形式吗?你能得到什么?
(1)两组对边分别相等的四边形是平行四边形;
提示 若四边形的两组对边分别相等,则这个四边形是平行四边形.
(2)一组对边平行且相等的四边形是平行四边形;
提示 若四边形的一组对边平行且相等,则这个四边形是平行四边形.
(3)两条对角线互相平分的四边形是平行四边形;
提示 若四边形的两条对角线互相平分,则这个四边形是平行四边形.
(4)平行四边形的两组对边分别相等;
提示 若四边形是平行四边形,则四边形的两组对边分别相等.
(5)平行四边形的一组对边平行且相等;
提示 若四边形是平行四边形,则四边形的一组对边平行且相等.
(6)平行四边形的两条对角线互相平分.
提示 若四边形是平行四边形,则四边形的两条对角线互相平分.
由此可见,数学中的每一条判定定理都给出了相应数学结论成立的一个充分条件,即使结论成立的条件并不唯一.数学中的每一条性质定理都给出了相应数学结论成立的一个必要条件,即所获得的结论也不唯一.
知识梳理
充分条件与必要条件
“若p,则q”为真命题 “若p,则q”为假命题
推出关系 p q p q
条件关系 p是q的 条件 q是p的 条件 p不是q的 条件
q不是p的 条件
定理关系 判定定理给出了相应数学结论成立的充分条件 性质定理给出了相应数学结论成立的必要条件
充分
必要
充分
必要
(1)前提p q,有方向,条件在前,结论在后.
(2)若p q,则p是q的充分条件或q是p的必要条件.
(3)“p是q的充分条件”,“q是p的必要条件”,“q的一个充分条件是p”,“p的一个必要条件是q”,说的是同一个意思.
注意点:
(1)指出下列哪些命题中p是q的充分条件?
①在△ABC中,p:∠B>∠C,q:AC>AB;
例1
在△ABC中,由大角对大边知,∠B>∠C AC>AB,所以p是q的充分条件.
②已知x,y∈R,p:x=1,q:(x-1)(x-2)=0;
由x=1 (x-1)(x-2)=0,故p是q的充分条件.
③已知x∈R,p:x>1,q:x>2.
方法一 由x>1 x>2,所以p不是q的充分条件.
方法二 设集合A={x|x>1},B={x|x>2},
所以B A,所以p不是q的充分条件.
(2)指出下列哪些命题中q是p的必要条件?
①p:一个四边形是矩形,q:四边形的对角线相等;
因为矩形的对角线相等,所以q是p的必要条件.
②p:A B,q:A∩B=A;
因为p q,
所以q是p的必要条件.
③p:a>b,q:ac>bc.
因为p q,
所以q不是p的必要条件.
充分、必要条件的判断方法
(1)判断p是q的什么条件,主要判断若p成立时,能否推出q成立,反过来,若q成立时,能否推出p成立;若p q为真,则p是q的充分条件,若q p为真,则p是q的必要条件.
(2)也可利用集合的关系判断,如果条件甲“x∈A”,条件乙“x∈B”.若A B,则甲是乙的必要条件.
反思感悟
跟踪训练1
分析下列各项中p与q的关系.
(1)p:α为锐角,q:α=45°.
由于q p,p q,故p是q的必要条件,q是p的充分条件.
(2)p:(x+1)(x-2)=0,q:x+1=0.
由于q p,p q,故p是q的必要条件,q是p的充分条件.
充分条件与必要条件的应用
二
已知集合P={x|-2<x<4},Q={x|3m-2≤x≤5m+2,m∈R}.若P的充分条件为Q,求实数m的取值范围.
例2
由已知,P的充分条件为Q,则Q是P的子集.
当3m-2>5m+2,即m<-2时,Q= ,满足题意,
当3m-2≤5m+2,即m≥-2时,
延伸探究 已知集合P={x|-2<x<1},Q={x|3m-2≤x≤5m+2,m∈R}.若P的必要条件为Q,求实数m的取值范围.
由题意得,P是Q的子集,
充分条件与必要条件的应用技巧
(1)应用:可利用充分性与必要性进行相关问题的求解,特别是求参数的值或取值范围问题.
(2)求解步骤:先把p,q等价转化,利用充分条件、必要条件与集合间的包含关系,建立关于参数的不等式(组)进行求解.
反思感悟
已知P={x|a-4
因为“x∈P”是“x∈Q”的必要条件,
所以Q P,
-1≤a≤5
课堂
小结
1.知识清单:
(1)充分条件、必要条件的概念.
(2)充分条件与判定定理,必要条件与性质定理的关系.
(3)充分条件、必要条件的判断.
(4)充分条件与必要条件的应用.
2.方法归纳:等价转化.
3.常见误区:充分条件、必要条件不唯一;求参数范围时能否取到端点值.
随堂演练
1.若p是q的充分条件,则q是p的
A.充分条件
B.必要条件
C.既不是充分条件也不是必要条件
D.既是充分条件又是必要条件
√
1
2
3
4
因为p是q的充分条件,所以p q,
所以q是p的必要条件.
2.“四边形的四条边相等”是“四边形是正方形”的
A.充分条件
B.必要条件
C.既是充分条件又是必要条件
D.既不是充分条件也不是必要条件
√
1
2
3
4
因为正方形的四条边相等,但四条边相等的四边形不一定是正方形,所以“四边形的四条边相等”是“四边形是正方形”的必要条件.
3.使x>3成立的一个充分条件是
A.x>4 B.x>0
C.x>2 D.x<2
√
1
2
3
4
只有x>4 x>3,其他选项均不可推出x>3.
4.若“x>1”是“x>a”的充分条件,则a的取值范围是______.
1
2
3
4
a≤1
因为x>1 x>a,所以a≤1.
课时对点练
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
1.下列命题中,p是q的充分条件的是
A.p:ab≠0,q:a≠0
B.p:a2+b2≥0,q:a≥0且b≥0
C.p:x2>1,q:x>1
根据充分条件的概念逐一判断,
只有ab≠0 a≠0.
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2.使x>1成立的一个必要条件是
A.x>0 B.x>3 C.x>2 D.x<2
√
只有x>1 x>0,其他选项均不可由x>1推出.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.已知集合A={3,m},B={1,3,5},则m=1是A B的
A.充分条件 B.必要条件
C.既不是充分条件也不是必要条件 D.既是充分条件又是必要条件
√
若A B,则有m∈B且m≠3,所以m=1或m=5,故当m=1时,有A B,而A B时,m不一定是1,故m=1是A B的充分条件,不是必要条件.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.下列“若p,则q”形式的命题中,满足p是q的充分条件的是
A.若平面内点P在线段AB的垂直平分线上,则PA=PB
B.若x是无理数,则x2也是无理数
C.若x>y,则x2>y2
D.若x2>y2,则x>y
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
线段垂直平分线上的点到两个端点的距离相等,故A正确;
若x= ,则x2=2,故B不成立;
若x=-1,y=-2,故C结论不成立;
若x=-2,y=1,故D结论不成立.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.(多选)下列说法不正确的是
A.“x>5”是“x>4”的充分条件
B.“xy=0”是“x=0且y=0”的充分条件
C.“-2
√
B中由xy=0不能推出x=0且y=0,故B不正确;
C中“-2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.(多选)使ab>0成立的充分条件是
A.a>0,b>0 B.a+b>0
C.a<0,b<0 D.a>1,b>1
√
因为a>0,b>0 ab>0;a<0,b<0 ab>0;a>1,b>1 ab>0,所以选项A,C,D都是使ab>0成立的充分条件.
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.设集合A={1,2},
(1)请写出一个集合B_______________________,使“x∈A”是“x∈B”的充分条件,但“x∈A”不是“x∈B”的必要条件;
(2)请写出一个集合B_____________________,使“x∈A”是“x∈B”的必要条件,但“x∈A”不是“x∈B”的充分条件.
B={1,2,3}(答案不唯一)
B={1}(答案不唯一)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.条件p:2-x>0,条件q:x
{a|a≥2}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.指出下列命题中,p是q的什么条件?
(2)p:a2+b2=0,q:a+b=0;
∵a2+b2=0 a=b=0 a+b=0,a+b=0 a2+b2=0,∴p是q的充分条件.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(3)p:(x-1)2+(y-2)2=0,q:(x-1)(y-2)=0.
∵(x-1)2+(y-2)2=0 x=1且y=2 (x-1)(y-2)=0,
而(x-1)(y-2)=0 (x-1)2+(y-2)2=0,∴p是q的充分条件.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.已知p:-1
由于p:-1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
11.设x,y是两个实数,命题:“x,y中至少有一个数大于1”的充分条件是
A.x+y=2 B.x+y>2
C.x2+y2>2 D.xy>1
√
对于选项A,当x=1,y=1时,满足x+y=2,但命题不成立;
对于选项C,D,当x=-2,y=-3时,满足x2+y2>2,xy>1,但命题不成立,也不符合题意.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.集合A={x|-1
A={x|-1
所以-1≤b-1<1或-1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.设甲、乙、丙是三个命题,如果甲是乙的必要条件,丙是乙的充分条件,但不是乙的必要条件,那么
A.丙是甲的充分条件,但不是甲的必要条件
B.丙是甲的必要条件,但不是甲的充分条件
C.丙既是甲的充分条件,又是甲的必要条件
D.丙既不是甲的充分条件,也不是甲的必要条件
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为甲是乙的必要条件,所以乙 甲.
又因为丙是乙的充分条件,但不是乙的必要条件,所
以丙 乙,但乙 丙,如图.
综上,有丙 甲,但甲 丙,
即丙是甲的充分条件,但不是甲的必要条件.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.已知p:x<-2或x>10,q:x<1+a或x>1-a(a<0).若p是q的必要条件,则实数a的取值范围为___________.
∵p是q的必要条件,∴q p,
{a|a≤-9}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
15.“一元二次方程x2-ax+1=0有两个正实数根”的一个充分条件可以为_________________;一个必要条件可以为____________________.
因为一元二次方程x2-ax+1=0有两个正实数根,
a>3(答案不唯一)
a>-1(答案不唯一)
故一元二次方程x2-ax+1=0有两个正实数根的一个充分条件可以为a>3;
一元二次方程x2-ax+1=0有两个正实数根的一个必要条件可以为a>-1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.(1)是否存在实数m,使2x+m<0是x<-1或x>3的充分条件?
欲使2x+m<0是x<-1或x>3的充分条件,
所以m≥2.
故存在实数m≥2,使2x+m<0是x<-1或x>3的充分条件.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)是否存在实数m,使2x+m<0是x<-1或x>3的必要条件?
欲使2x+m<0是x<-1或x>3的必要条件,
则只要{x|x<-1或x>3} ,这是不可能的.
故不存在实数m,使2x+m<0是x<-1或x>3的必要条件.
本课结束
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
