2022-2023学年人教A版2019高中数学 必修1 4.2.1 指数函数的概念 课件(56张PPT)
文档属性
| 名称 | 2022-2023学年人教A版2019高中数学 必修1 4.2.1 指数函数的概念 课件(56张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-27 00:00:00 | ||
图片预览










文档简介
(共56张PPT)
4.2.1 指数函数的概念
第四章 §4.2 指数函数
学习目标
1.理解指数函数的概念,了解对底数的限制条件的合理性.
2.了解指数增长型和指数衰减型在实际问题中的应用.
导语
话说一个毕业生去求职,当和老板讨论薪资的时候,他说:“老板,不如这样吧,我第一个月只要1元,第二个月要2元,第三个月要4元,这样以后每个月的薪资都是前一个月薪资的2倍,老板你看怎么样?”老板一听,这不多呀,当即拍板说:“好,就按你说的办,我们先签个3年的合同吧”,大家猜一下,第12个月,他能获得多少工资?(211=2 048)第24个月,他能获得多少工资?(223=8 388 608)估计这个老板肠子都悔青了,这就是我们今天要学习的指数函数.大家可以用这种方式向家长要个零花钱噢,但是周期千万不要太长,有个10天就可以了.
课时对点练
一、指数函数的概念
二、求指数函数的解析式或求值
三、指数增长型和指数衰减型函数的实际应用
随堂演练
内容索引
指数函数的概念
一
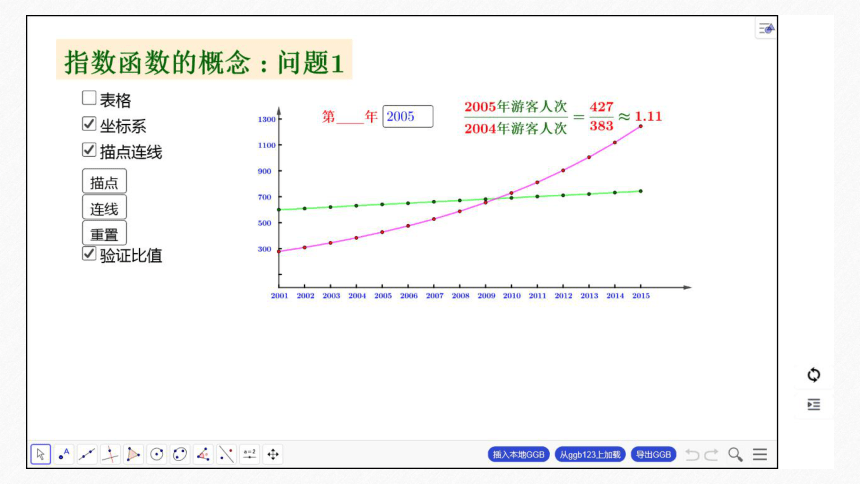
问题1 阅读课本111页~113页,你有什么样的收获?
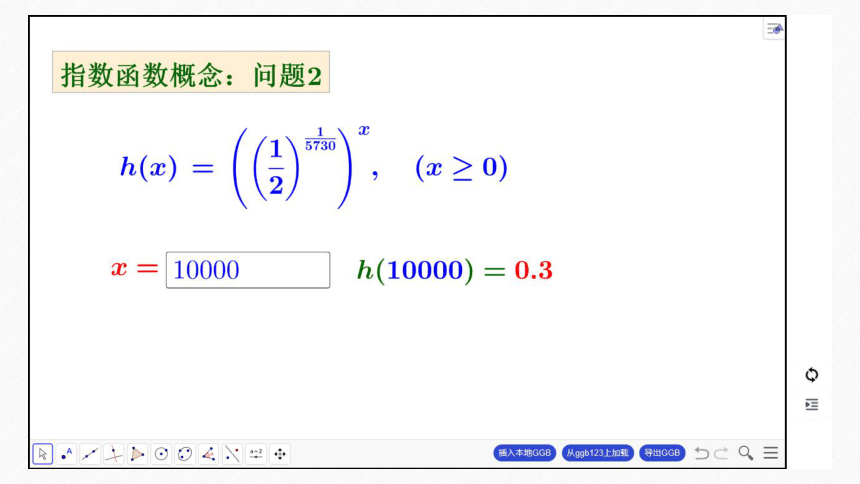
提示 由课本问题1中可知,B地景区的游客人次的年增长率是一个常数,问题2中的衰减率也是一个常数.函数y=1.11x(x∈[0,+∞))与函数y=
(x∈[0,+∞))的函数解析式都是指数形式,底数为定值,自变
量在指数位置.
具体过程详见下页GeoGebra动画演示.
知识梳理
指数函数的概念:一般地,函数 (a>0,且a≠1)叫做指数函数,其中指数x是自变量,函数的定义域是R.
y=ax
(1)函数的特征:底数a>0,且a≠1.
(2)指数幂的系数为1.
注意点:
(1)给出下列函数:①y=2·3x;②y=3x+1;③y=3x;④y=x3;
⑤y=(-2)x.其中,指数函数的个数是
A.0 B.1 C.2 D.4
例1
①中,3x的系数是2,故①不是指数函数;
②中,y=3x+1的指数是x+1,不是自变量x,故②不是指数函数;
③中,3x的系数是1,幂的指数是自变量x,且只有3x一项,故③是指数函数;
④中,y=x3的底数为自变量,指数为常数,故④不是指数函数;
⑤中,底数-2<0,不是指数函数.
√
(2)若函数y=(2a-1)x(x是自变量)是指数函数,则a的取值范围是
A.(0,1)∪(1,+∞) B.[0,1)∪(1,+∞)
依题意得2a-1>0,且2a-1≠1,
√
判断一个函数是否为指数函数的方法
(1)底数的值是否符合要求.
(2)ax前的系数是否为1.
(3)指数是否符合要求.
反思感悟
(1)下列是指数函数的是
A.y=-3x B.y=
C.y=ax D.y=πx
跟踪训练1
√
根据指数函数的特征知,A,B,C不是指数函数.
(2)若函数y=(a2-3a+3)·ax是指数函数,则a的值为_____.
由指数函数的定义知
2
①
②
由①得a=1或2,结合②得a=2.
求指数函数的解析式或求值
二
例2
因为函数f(x)是指数函数,
√
所以a=8,
(1)求指数函数的解析式时,一般采用待定系数法,即先设出函数的解析式,然后利用已知条件,求出解析式中的参数,从而得到函数的解析式,其中掌握指数函数的概念是解决这类问题的关键.
(2)求指数函数的函数值的关键是求出指数函数的解析式.
反思感悟
指数函数y=f(x)的图象经过点 ,那么f(2)·f(1)等于
A.-3 B.9
C.27 D.81
跟踪训练2
√
指数增长型和指数衰减型函数的实际应用
三
问题2 将一张报纸连续对折,折叠次数x与对应的层数y之间存在什么关系?对折后的面积S(设原面积为1)与折叠的次数有怎样的关系?
提示
折叠次数 对应层数 对折后的面积S
x=1 y=2=21
x=2 y=4=22
x=3 y=8=23
… … …
由上面的对应关系,我们可以归纳出第x次折叠后对应的层数为y=2x
(x∈N*),对折后的面积 (x∈N*).
知识梳理
1.y=kax(k>0,a>0且a≠1),当 时为指数增长型函数模型.
2.y=kax(k>0,a>0且a≠1),当 时为指数衰减型函数模型.
a>1
0 (1)某种细菌经60分钟培养,可繁殖为原来的2倍,且知该细菌的繁殖规律为y=10ekt,其中k为常数,t表示时间(单位:小时),y表示细菌个数,10个细菌经过7小时培养,细菌能达到的个数为
A.640 B.1 280
C.2 560 D.5 120
例3
√
延伸探究 将本例的条件变为“细菌经60分钟培养,可繁殖为原来的3倍”,其他的条件不变,试求经过7小时培养,细菌能达到的个数.
设原来的细菌数为a,由题意可得,
当a=10时,ek=3,所以y=10ekt=10·3t,
若t=7,则可得此时的细菌数为y=10×37=21 870.
(2)有容积相等的桶A和桶B,开始时桶A中有a升水,桶B中无水.现把桶A的水注入桶B,t分钟后,桶A的水剩余y1=amt(升),其中m为正常数.假设5分钟后,桶A和桶B的水相等,要使桶A的水只有 升,必须再经过
A.12分钟
B.15分钟
C.20分钟
D.25分钟
√
关于函数y=kax在实际问题中的应用
(1)函数y=kax是用来刻画指数增长或指数衰减变化规律的非常有用的函数模型,一般当k>0时,若a>1,则刻画指数增长变化规律;若0(2)解决此类问题可利用待定系数法,根据条件确定出解析式中的系数后,利用指数运算解题.
反思感悟
随着我国经济的不断发展,2018年年底某偏远地区农民人均年收入为3 000元,预计该地区今后农民的人均年收入将以每年6%的年平均增长率增长,那么2025年年底该地区的农民人均年收入为
A.3 000×1.06×7元 B.3 000×1.067元
C.3 000×1.06×8元 D.3 000×1.068元
跟踪训练3
√
设经过x年,该地区的农民人均年收入为y元,
根据题意可得y=3 000×1.06x,从2018到2025年共经过了7年,
所以2025年年底该地区的农民人均年收入为3 000×1.067元.
课堂
小结
1.知识清单:
(1)指数函数的定义.
(2)指数增长型和指数衰减型函数模型.
2.方法归纳:待定系数法.
3.常见误区:易忽视指数函数的底数a的限制条件:a>0且a≠1.
随堂演练
1.下列各函数中,是指数函数的是
A.y=(-4)x B.y=-4x
C.y=3x-1 D.y=
√
1
2
3
4
A中函数的底数不满足大于零,故不是指数函数;
B中函数式中幂值的系数不是1,故不是指数函数;
C中的指数是x-1,不是指数函数.
1
2
3
4
2.若函数y=(m2-m-1)·mx是指数函数,则m等于
A.-1或2 B.-1
C.2 D.
√
解得m=2(m=-1舍去).
1
2
3
4
3.为响应国家退耕还林的号召,某地的耕地面积在最近50年内减少了10%,如果按此规律,设2017年的耕地面积为m,则2022年的耕地面积为
A.(1-0.1250)m B.
C.0.9250m D.
√
设每年减少的百分率为a,
由题意得,(1-a)50=1-10%=0.9,
∴1-a= ,
由2017年的耕地面积为m,得2022年的耕地面积为(1-a)5m= .
1
2
3
4
4.若函数f(x)是指数函数,且f(2)=2,则f(x)= ________.
由题意,设f(x)=ax(a>0且a≠1),
课时对点练
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
1.下列函数是指数函数的是
A.y= B.y=(-8)x
C.y=2x-1 D.y=x2
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
对于D,函数y=x2,是幂函数,不是指数函数.
对于B,函数y=(-8)x中,a=-8<0,不是指数函数;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2.若指数函数f(x)的图象过点(4,81),则f(x)的解析式为
A.f(x)=x3 B.f(x)=3x
C.f(x)= D.f(x)=
√
设f(x)=ax(a>0,且a≠1),
由题意得a4=81,解得a=3,∴f(x)=3x.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.函数f(x)=(2a-3)ax是指数函数,则f(1)等于
A.8 B.
C.4 D.2
√
∵函数f(x)=(2a-3)ax是指数函数,
∴2a-3=1,解得a=2.
∴f(x)=2x,∴f(1)=2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.一种产品的成品是a元,今后m年内,计划使成本平均每年比上一年降低p%,成本y是经过年数x(0A.y=a(1+p%)x(0C.y=a(p%)x(0√
∵产品的成品是a元,1年后,成本为a-p%·a=a(1-p%);2年后,成本为a(1-p%)-a(1-p%)·p%=a(1-p%)2;…,
∴x年后,成本y=a(1-p%)x(01
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.函数f(x)=ax(a>0且a≠1),对于任意实数x,y都有
A.f(xy)=f(x)f(y)
B.f(xy)=f(x)+f(y)
C.f(x+y)=f(x)f(y)
D.f(x+y)=f(x)+f(y)
√
f(x+y)=ax+y=axay=f(x)f(y).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.(多选)若函数f(x)=(m2-2m-2)ax是指数函数,则实数m的值为
A.2 B.3 C.-1 D.1
√
∵函数f(x)=(m2-2m-2)ax是指数函数,
∴m2-2m-2=1,
解得m=3或-1.
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.若函数f(x)=(a-1)x是指数函数,则实数a的取值范围是_______________.
(1,2)∪(2,+∞)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.f(x)为指数函数,若f(x)过点(-2,4),则f(f(-1))=____.
设f(x)=ax(a>0且a≠1),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.某林区某年木材蓄积量为200万立方米,由于采取了封山育林、严禁采伐等措施,预计使木材蓄积量的年平均增长率能达到5%.若经过x年后,该林区的木材蓄积量为y万立方米,求y=f(x)的解析式,并写出此函数的定义域.
由题意得,
经过1年后,木材蓄积量y1=200(1+5%)=200×1.05,
经过2年后,木材蓄积量y2=200×1.05×(1+5%)=200×1.052,
经过x年后,木材蓄积量y=200×1.05x.
定义域为N*.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.已知函数f(x)=(a2+a-5)ax是指数函数.
(1)求f(x)的表达式;
∴f(x)=2x.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
F(x)=f(x)-f(-x)是奇函数,证明如下:
F(x)=2x-2-x,定义域为R,
∴F(-x)=2-x-2x=-F(x),
∴F(x)是奇函数.
(2)判断F(x)=f(x)-f(-x)的奇偶性,并加以证明.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
11.已知集合A={-1,0,1},B={y|y=ex,x∈A},则A∩B等于
A.{0} B.{1} C.{-1} D.{0,1}
√
因此A∩B={1}.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.函数y=f(x)是R上的奇函数,当x<0时,f(x)=2x,则当x>0时,f(x)等于
A.-2x B.2-x C.-2-x D.2x
√
当x<0时,f(x)=2x,
当x>0时,-x<0,则f(-x)=2-x.
又f(x)是R上的奇函数,
所以当x>0时,f(x)=-f(-x)=-2-x.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴f(x)=2×4x.
f(x)=2×4x
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.某工厂2018年的产值为a万元,预计产值每年以7%的速度增加,则该厂到2022年的产值为__________万元.
2018年产值为a,增长率为7%;
2019年产值为a+a×7%=a(1+7%)(万元);
2020年产值为a(1+7%)+a(1+7%)×7%=a(1+7%)2(万元);
……;
2022年的产值为a(1+7%)4万元.
a(1+7%)4
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
15.某校甲、乙两食堂某年1月份的营业额相等,甲食堂的营业额逐月增加,并且每月的增加值相同;乙食堂的营业额也逐月增加,且每月增加的百分率相同.已知该年9月份两食堂的营业额又相等,则该年5月份
A.甲食堂的营业额较高
B.乙食堂的营业额较高
C.甲、乙两食堂的营业额相等
D.不能确定甲、乙哪个食堂的营业额较高
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.牛奶保鲜时间因储藏温度的不同而不同,假定保鲜时间y与储藏温度x的关系式为y=kerx(k,r为常数).若牛奶在0 ℃的冰箱中,保鲜时间约是100 h,在5 ℃的冰箱中,保鲜时间约是80 h,那么在10 ℃的冰箱中的保鲜时间是多少?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为保鲜时间y与储藏温度x的关系式为y=kerx(k,r为常数),
所以在10 ℃的冰箱中的保鲜时间为64 h.
本课结束
4.2.1 指数函数的概念
第四章 §4.2 指数函数
学习目标
1.理解指数函数的概念,了解对底数的限制条件的合理性.
2.了解指数增长型和指数衰减型在实际问题中的应用.
导语
话说一个毕业生去求职,当和老板讨论薪资的时候,他说:“老板,不如这样吧,我第一个月只要1元,第二个月要2元,第三个月要4元,这样以后每个月的薪资都是前一个月薪资的2倍,老板你看怎么样?”老板一听,这不多呀,当即拍板说:“好,就按你说的办,我们先签个3年的合同吧”,大家猜一下,第12个月,他能获得多少工资?(211=2 048)第24个月,他能获得多少工资?(223=8 388 608)估计这个老板肠子都悔青了,这就是我们今天要学习的指数函数.大家可以用这种方式向家长要个零花钱噢,但是周期千万不要太长,有个10天就可以了.
课时对点练
一、指数函数的概念
二、求指数函数的解析式或求值
三、指数增长型和指数衰减型函数的实际应用
随堂演练
内容索引
指数函数的概念
一
问题1 阅读课本111页~113页,你有什么样的收获?
提示 由课本问题1中可知,B地景区的游客人次的年增长率是一个常数,问题2中的衰减率也是一个常数.函数y=1.11x(x∈[0,+∞))与函数y=
(x∈[0,+∞))的函数解析式都是指数形式,底数为定值,自变
量在指数位置.
具体过程详见下页GeoGebra动画演示.
知识梳理
指数函数的概念:一般地,函数 (a>0,且a≠1)叫做指数函数,其中指数x是自变量,函数的定义域是R.
y=ax
(1)函数的特征:底数a>0,且a≠1.
(2)指数幂的系数为1.
注意点:
(1)给出下列函数:①y=2·3x;②y=3x+1;③y=3x;④y=x3;
⑤y=(-2)x.其中,指数函数的个数是
A.0 B.1 C.2 D.4
例1
①中,3x的系数是2,故①不是指数函数;
②中,y=3x+1的指数是x+1,不是自变量x,故②不是指数函数;
③中,3x的系数是1,幂的指数是自变量x,且只有3x一项,故③是指数函数;
④中,y=x3的底数为自变量,指数为常数,故④不是指数函数;
⑤中,底数-2<0,不是指数函数.
√
(2)若函数y=(2a-1)x(x是自变量)是指数函数,则a的取值范围是
A.(0,1)∪(1,+∞) B.[0,1)∪(1,+∞)
依题意得2a-1>0,且2a-1≠1,
√
判断一个函数是否为指数函数的方法
(1)底数的值是否符合要求.
(2)ax前的系数是否为1.
(3)指数是否符合要求.
反思感悟
(1)下列是指数函数的是
A.y=-3x B.y=
C.y=ax D.y=πx
跟踪训练1
√
根据指数函数的特征知,A,B,C不是指数函数.
(2)若函数y=(a2-3a+3)·ax是指数函数,则a的值为_____.
由指数函数的定义知
2
①
②
由①得a=1或2,结合②得a=2.
求指数函数的解析式或求值
二
例2
因为函数f(x)是指数函数,
√
所以a=8,
(1)求指数函数的解析式时,一般采用待定系数法,即先设出函数的解析式,然后利用已知条件,求出解析式中的参数,从而得到函数的解析式,其中掌握指数函数的概念是解决这类问题的关键.
(2)求指数函数的函数值的关键是求出指数函数的解析式.
反思感悟
指数函数y=f(x)的图象经过点 ,那么f(2)·f(1)等于
A.-3 B.9
C.27 D.81
跟踪训练2
√
指数增长型和指数衰减型函数的实际应用
三
问题2 将一张报纸连续对折,折叠次数x与对应的层数y之间存在什么关系?对折后的面积S(设原面积为1)与折叠的次数有怎样的关系?
提示
折叠次数 对应层数 对折后的面积S
x=1 y=2=21
x=2 y=4=22
x=3 y=8=23
… … …
由上面的对应关系,我们可以归纳出第x次折叠后对应的层数为y=2x
(x∈N*),对折后的面积 (x∈N*).
知识梳理
1.y=kax(k>0,a>0且a≠1),当 时为指数增长型函数模型.
2.y=kax(k>0,a>0且a≠1),当 时为指数衰减型函数模型.
a>1
0
A.640 B.1 280
C.2 560 D.5 120
例3
√
延伸探究 将本例的条件变为“细菌经60分钟培养,可繁殖为原来的3倍”,其他的条件不变,试求经过7小时培养,细菌能达到的个数.
设原来的细菌数为a,由题意可得,
当a=10时,ek=3,所以y=10ekt=10·3t,
若t=7,则可得此时的细菌数为y=10×37=21 870.
(2)有容积相等的桶A和桶B,开始时桶A中有a升水,桶B中无水.现把桶A的水注入桶B,t分钟后,桶A的水剩余y1=amt(升),其中m为正常数.假设5分钟后,桶A和桶B的水相等,要使桶A的水只有 升,必须再经过
A.12分钟
B.15分钟
C.20分钟
D.25分钟
√
关于函数y=kax在实际问题中的应用
(1)函数y=kax是用来刻画指数增长或指数衰减变化规律的非常有用的函数模型,一般当k>0时,若a>1,则刻画指数增长变化规律;若0
反思感悟
随着我国经济的不断发展,2018年年底某偏远地区农民人均年收入为3 000元,预计该地区今后农民的人均年收入将以每年6%的年平均增长率增长,那么2025年年底该地区的农民人均年收入为
A.3 000×1.06×7元 B.3 000×1.067元
C.3 000×1.06×8元 D.3 000×1.068元
跟踪训练3
√
设经过x年,该地区的农民人均年收入为y元,
根据题意可得y=3 000×1.06x,从2018到2025年共经过了7年,
所以2025年年底该地区的农民人均年收入为3 000×1.067元.
课堂
小结
1.知识清单:
(1)指数函数的定义.
(2)指数增长型和指数衰减型函数模型.
2.方法归纳:待定系数法.
3.常见误区:易忽视指数函数的底数a的限制条件:a>0且a≠1.
随堂演练
1.下列各函数中,是指数函数的是
A.y=(-4)x B.y=-4x
C.y=3x-1 D.y=
√
1
2
3
4
A中函数的底数不满足大于零,故不是指数函数;
B中函数式中幂值的系数不是1,故不是指数函数;
C中的指数是x-1,不是指数函数.
1
2
3
4
2.若函数y=(m2-m-1)·mx是指数函数,则m等于
A.-1或2 B.-1
C.2 D.
√
解得m=2(m=-1舍去).
1
2
3
4
3.为响应国家退耕还林的号召,某地的耕地面积在最近50年内减少了10%,如果按此规律,设2017年的耕地面积为m,则2022年的耕地面积为
A.(1-0.1250)m B.
C.0.9250m D.
√
设每年减少的百分率为a,
由题意得,(1-a)50=1-10%=0.9,
∴1-a= ,
由2017年的耕地面积为m,得2022年的耕地面积为(1-a)5m= .
1
2
3
4
4.若函数f(x)是指数函数,且f(2)=2,则f(x)= ________.
由题意,设f(x)=ax(a>0且a≠1),
课时对点练
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
1.下列函数是指数函数的是
A.y= B.y=(-8)x
C.y=2x-1 D.y=x2
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
对于D,函数y=x2,是幂函数,不是指数函数.
对于B,函数y=(-8)x中,a=-8<0,不是指数函数;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2.若指数函数f(x)的图象过点(4,81),则f(x)的解析式为
A.f(x)=x3 B.f(x)=3x
C.f(x)= D.f(x)=
√
设f(x)=ax(a>0,且a≠1),
由题意得a4=81,解得a=3,∴f(x)=3x.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.函数f(x)=(2a-3)ax是指数函数,则f(1)等于
A.8 B.
C.4 D.2
√
∵函数f(x)=(2a-3)ax是指数函数,
∴2a-3=1,解得a=2.
∴f(x)=2x,∴f(1)=2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.一种产品的成品是a元,今后m年内,计划使成本平均每年比上一年降低p%,成本y是经过年数x(0
∵产品的成品是a元,1年后,成本为a-p%·a=a(1-p%);2年后,成本为a(1-p%)-a(1-p%)·p%=a(1-p%)2;…,
∴x年后,成本y=a(1-p%)x(0
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.函数f(x)=ax(a>0且a≠1),对于任意实数x,y都有
A.f(xy)=f(x)f(y)
B.f(xy)=f(x)+f(y)
C.f(x+y)=f(x)f(y)
D.f(x+y)=f(x)+f(y)
√
f(x+y)=ax+y=axay=f(x)f(y).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.(多选)若函数f(x)=(m2-2m-2)ax是指数函数,则实数m的值为
A.2 B.3 C.-1 D.1
√
∵函数f(x)=(m2-2m-2)ax是指数函数,
∴m2-2m-2=1,
解得m=3或-1.
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.若函数f(x)=(a-1)x是指数函数,则实数a的取值范围是_______________.
(1,2)∪(2,+∞)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.f(x)为指数函数,若f(x)过点(-2,4),则f(f(-1))=____.
设f(x)=ax(a>0且a≠1),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.某林区某年木材蓄积量为200万立方米,由于采取了封山育林、严禁采伐等措施,预计使木材蓄积量的年平均增长率能达到5%.若经过x年后,该林区的木材蓄积量为y万立方米,求y=f(x)的解析式,并写出此函数的定义域.
由题意得,
经过1年后,木材蓄积量y1=200(1+5%)=200×1.05,
经过2年后,木材蓄积量y2=200×1.05×(1+5%)=200×1.052,
经过x年后,木材蓄积量y=200×1.05x.
定义域为N*.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.已知函数f(x)=(a2+a-5)ax是指数函数.
(1)求f(x)的表达式;
∴f(x)=2x.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
F(x)=f(x)-f(-x)是奇函数,证明如下:
F(x)=2x-2-x,定义域为R,
∴F(-x)=2-x-2x=-F(x),
∴F(x)是奇函数.
(2)判断F(x)=f(x)-f(-x)的奇偶性,并加以证明.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
11.已知集合A={-1,0,1},B={y|y=ex,x∈A},则A∩B等于
A.{0} B.{1} C.{-1} D.{0,1}
√
因此A∩B={1}.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.函数y=f(x)是R上的奇函数,当x<0时,f(x)=2x,则当x>0时,f(x)等于
A.-2x B.2-x C.-2-x D.2x
√
当x<0时,f(x)=2x,
当x>0时,-x<0,则f(-x)=2-x.
又f(x)是R上的奇函数,
所以当x>0时,f(x)=-f(-x)=-2-x.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴f(x)=2×4x.
f(x)=2×4x
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.某工厂2018年的产值为a万元,预计产值每年以7%的速度增加,则该厂到2022年的产值为__________万元.
2018年产值为a,增长率为7%;
2019年产值为a+a×7%=a(1+7%)(万元);
2020年产值为a(1+7%)+a(1+7%)×7%=a(1+7%)2(万元);
……;
2022年的产值为a(1+7%)4万元.
a(1+7%)4
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
15.某校甲、乙两食堂某年1月份的营业额相等,甲食堂的营业额逐月增加,并且每月的增加值相同;乙食堂的营业额也逐月增加,且每月增加的百分率相同.已知该年9月份两食堂的营业额又相等,则该年5月份
A.甲食堂的营业额较高
B.乙食堂的营业额较高
C.甲、乙两食堂的营业额相等
D.不能确定甲、乙哪个食堂的营业额较高
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.牛奶保鲜时间因储藏温度的不同而不同,假定保鲜时间y与储藏温度x的关系式为y=kerx(k,r为常数).若牛奶在0 ℃的冰箱中,保鲜时间约是100 h,在5 ℃的冰箱中,保鲜时间约是80 h,那么在10 ℃的冰箱中的保鲜时间是多少?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为保鲜时间y与储藏温度x的关系式为y=kerx(k,r为常数),
所以在10 ℃的冰箱中的保鲜时间为64 h.
本课结束
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
