2022-2023学年人教A版2019高中数学必修1 5.2.2 同角三角函数的基本关系 课件(66张PPT)
文档属性
| 名称 | 2022-2023学年人教A版2019高中数学必修1 5.2.2 同角三角函数的基本关系 课件(66张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-27 14:58:58 | ||
图片预览








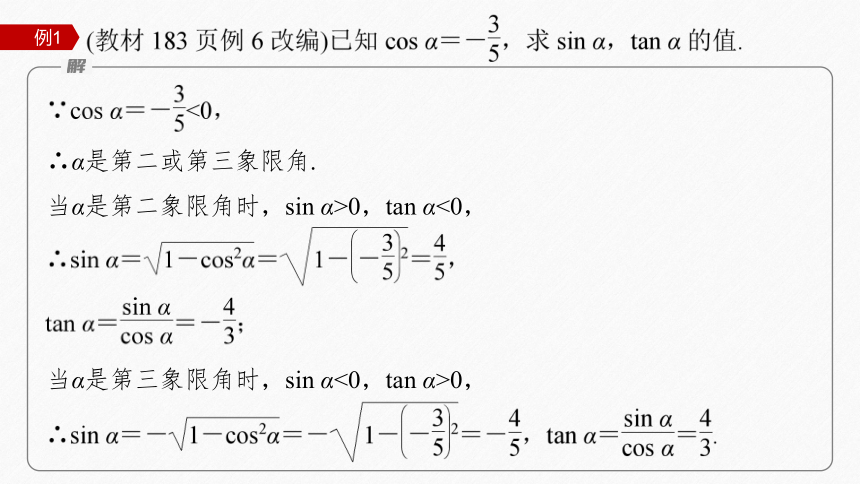


文档简介
(共66张PPT)
5.2.2 同角三角函数的基本关系
第五章 §5.2 三角函数的概念
学习目标
1.理解并掌握同角三角函数的基本关系.
2.会用同角三角函数的基本关系进行三角函数式的求值、化简和证明.
导语
“一支竹篙啊,难渡汪洋海,众人划桨哟,开动大帆船,一棵小树呀,弱不禁风雨,百里森林哟,并肩耐岁寒,耐岁寒,一加十,十加百,百加千千万,你加我,我加你,大家心相连,同舟共济海让路,号子嘛一喊浪靠边,百舸嘛争流千帆进,波涛在后岸在前……”伴随着一首经典老歌,让我们感触很深,歌词中每一句都流露出了“团结就是力量,团结就是胜利”,就像是我们数学中的每一个知识点一样,彼此紧密联系,比如我们刚学过的正弦、余弦和正切函数,它们之间到底有什么样的联系呢,让我们一起去发现.
课时对点练
一、利用同角三角函数的关系求值
二、利用同角三角函数的关系化简
三、一般恒等式的证明
随堂演练
内容索引
利用同角三角函数的关系求值
一
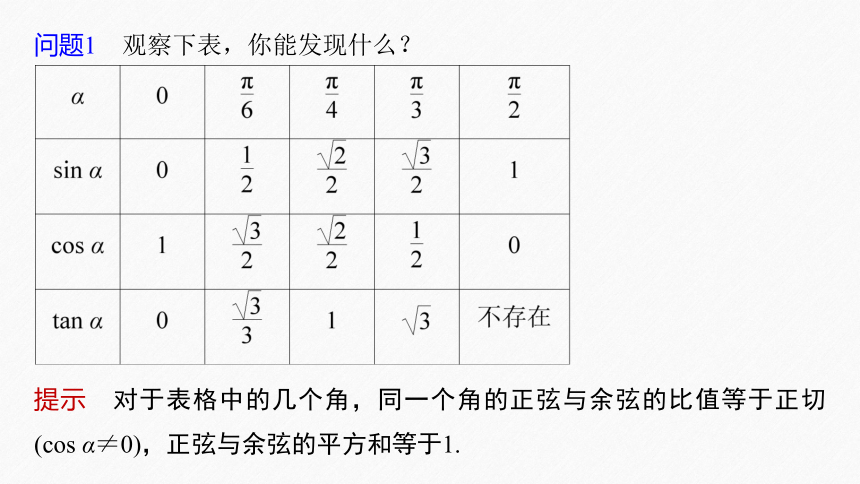
问题1 观察下表,你能发现什么?
提示 对于表格中的几个角,同一个角的正弦与余弦的比值等于正切(cos α≠0),正弦与余弦的平方和等于1.
问题2 若P(x,y)是角α的终边与单位圆的交点,则角α的三个三角函数值之间有什么联系?
提示 若余弦不为0,则正切等于正弦比余弦;因为点P在单位圆上,则由勾股定理得x2+y2=1.
知识梳理
tan α
1
注意点:
例1
∴α是第二或第三象限角.
当α是第二象限角时,sin α>0,tan α<0,
当α是第三象限角时,sin α<0,tan α>0,
反思感悟
反思感悟
跟踪训练1
已知sin α+3cos α=0,求sin α,cos α的值.
∵sin α+3cos α=0,
∴sin α=-3cos α.
又sin2α+cos2α=1,
∴(-3cos α)2+cos2α=1,
即10cos2α=1,
又由sin α=-3cos α,可知sin α与cos α异号,
∴角α的终边在第二或第四象限.
当角α的终边在第二象限时,
当角α的终边在第四象限时,
利用同角三角函数的关系化简
二
问题3 你能发现同角三角函数的哪些变形形式?
利用上述变换我们可以对三角函数式进行化简,也就是代数式的恒等变换,要使结果尽可能的简单,也就是项数尽可能的少,次数尽可能的低,函数种类尽可能的少,式子中尽量不含根号,能求值的尽量求值.
提示 sin2α+cos2α=1
例2
化简:
三角函数式的化简技巧
(1)化切为弦,即把正切都化为正弦、余弦,从而减少函数名称,达到化繁为简的目的.
(2)对于含有根号的,常把根号里面的部分化成完全平方式,然后去根号达到化简的目的.
(3)对于化简含高次的三角函数式,往往借助于因式分解,或构造sin2α+cos2α=1,以降低函数次数,达到化简的目的.
反思感悟
跟踪训练2
=1+1=2.
一般恒等式的证明
三
例3
所以原等式成立.
所以原等式成立.
反思感悟
证明三角恒等式常用的方法
(1)从左向右推导或从右向左推导,一般由繁到简.
(2)左右归一法,即证明左右两边都等于同一个式子.
(3)化异为同法,即针对题设与结论间的差异,有针对地变形,以消除差异.
注意点:
(1)证明三角恒等式的实质:清楚等式两端的差异,有目的地化简.
(2)基本原则:由繁到简.
(3)常用方法:从左向右证,从右向左证,左右同时证.
跟踪训练3
所以原等式成立.
课堂
小结
1.知识清单:
(1)同角三角函数的基本关系.
(2)利用同角三角函数的基本关系求值、化简与证明.
2.方法归纳:由部分到整体、整体代换法.
3.常见误区:求值时注意α的范围,如果无法确定,一定要对α所在的象限进行分类讨论.
随堂演练
1
2
3
4
√
√
1
2
3
4
1
2
3
4
√
1
2
3
4
1
2
3
4
1
2
3
4
1
2
3
4
课时对点练
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
由条件知α是第四象限角,所以sin α<0,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
原式=sin2α+cos2α(cos2α+sin2α)
=sin2α+cos2α=1.
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为α为第二象限角,所以sin α>0,cos α<0,
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
由sin2α+cos2α=1,得1-cos2α=sin2α,
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
当x为第一象限角时,sin x>0,cos x>0,则f(x)=2+1=3,
当x为第二象限角时,sin x>0,cos x<0,则f(x)=2-1=1,
当x为第三象限角时,sin x<0,cos x<0,则f(x)=-2-1=-3,
当x为第四象限角时,sin x<0,cos x>0,则f(x)=-2+1=-1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.化简(1+tan215°)·cos215°= .
1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.设a>0且a≠1,若loga(sin x-cos x)=0,则sin8x+cos8x= .
1
因为a>0且a≠1,若loga(sin x-cos x)=0,
则sin x-cos x=a0=1,
所以(sin x-cos x)2=sin2x+cos2x-2sin xcos x=1,
又sin2x+cos2x=1,所以sin xcos x=0,
又由(sin2x+cos2x)2=sin4x+cos4x+2sin2x·cos2x=1,
得sin4x+cos4x=1,
所以sin8x+cos8x=(sin4x+cos4x)2-2sin4x·cos4x=(sin4x+cos4x)2=1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴α是第二或第三象限角.
当α是第二象限角时,则
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为α是第二象限角,
所以sin α>0,cos α<0.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∵α是第二象限角,且tan α=m,
∴m<0,sin α>0,cos α<0,mcos α=sin α,
代入平方关系得到m2cos2α+cos2α=1,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
8
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解得m=8.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)任取一个α的值,分别计算sin4α-cos4α,sin2α-cos2α,你又有什么发现?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(3)证明: x∈R,sin2x-cos2x=sin4x-cos4x.
对于任意实数x,都有sin2x-cos2x=(sin2x-cos2x)·(sin2x+cos2x)=sin4x-cos4x.
本课结束
5.2.2 同角三角函数的基本关系
第五章 §5.2 三角函数的概念
学习目标
1.理解并掌握同角三角函数的基本关系.
2.会用同角三角函数的基本关系进行三角函数式的求值、化简和证明.
导语
“一支竹篙啊,难渡汪洋海,众人划桨哟,开动大帆船,一棵小树呀,弱不禁风雨,百里森林哟,并肩耐岁寒,耐岁寒,一加十,十加百,百加千千万,你加我,我加你,大家心相连,同舟共济海让路,号子嘛一喊浪靠边,百舸嘛争流千帆进,波涛在后岸在前……”伴随着一首经典老歌,让我们感触很深,歌词中每一句都流露出了“团结就是力量,团结就是胜利”,就像是我们数学中的每一个知识点一样,彼此紧密联系,比如我们刚学过的正弦、余弦和正切函数,它们之间到底有什么样的联系呢,让我们一起去发现.
课时对点练
一、利用同角三角函数的关系求值
二、利用同角三角函数的关系化简
三、一般恒等式的证明
随堂演练
内容索引
利用同角三角函数的关系求值
一
问题1 观察下表,你能发现什么?
提示 对于表格中的几个角,同一个角的正弦与余弦的比值等于正切(cos α≠0),正弦与余弦的平方和等于1.
问题2 若P(x,y)是角α的终边与单位圆的交点,则角α的三个三角函数值之间有什么联系?
提示 若余弦不为0,则正切等于正弦比余弦;因为点P在单位圆上,则由勾股定理得x2+y2=1.
知识梳理
tan α
1
注意点:
例1
∴α是第二或第三象限角.
当α是第二象限角时,sin α>0,tan α<0,
当α是第三象限角时,sin α<0,tan α>0,
反思感悟
反思感悟
跟踪训练1
已知sin α+3cos α=0,求sin α,cos α的值.
∵sin α+3cos α=0,
∴sin α=-3cos α.
又sin2α+cos2α=1,
∴(-3cos α)2+cos2α=1,
即10cos2α=1,
又由sin α=-3cos α,可知sin α与cos α异号,
∴角α的终边在第二或第四象限.
当角α的终边在第二象限时,
当角α的终边在第四象限时,
利用同角三角函数的关系化简
二
问题3 你能发现同角三角函数的哪些变形形式?
利用上述变换我们可以对三角函数式进行化简,也就是代数式的恒等变换,要使结果尽可能的简单,也就是项数尽可能的少,次数尽可能的低,函数种类尽可能的少,式子中尽量不含根号,能求值的尽量求值.
提示 sin2α+cos2α=1
例2
化简:
三角函数式的化简技巧
(1)化切为弦,即把正切都化为正弦、余弦,从而减少函数名称,达到化繁为简的目的.
(2)对于含有根号的,常把根号里面的部分化成完全平方式,然后去根号达到化简的目的.
(3)对于化简含高次的三角函数式,往往借助于因式分解,或构造sin2α+cos2α=1,以降低函数次数,达到化简的目的.
反思感悟
跟踪训练2
=1+1=2.
一般恒等式的证明
三
例3
所以原等式成立.
所以原等式成立.
反思感悟
证明三角恒等式常用的方法
(1)从左向右推导或从右向左推导,一般由繁到简.
(2)左右归一法,即证明左右两边都等于同一个式子.
(3)化异为同法,即针对题设与结论间的差异,有针对地变形,以消除差异.
注意点:
(1)证明三角恒等式的实质:清楚等式两端的差异,有目的地化简.
(2)基本原则:由繁到简.
(3)常用方法:从左向右证,从右向左证,左右同时证.
跟踪训练3
所以原等式成立.
课堂
小结
1.知识清单:
(1)同角三角函数的基本关系.
(2)利用同角三角函数的基本关系求值、化简与证明.
2.方法归纳:由部分到整体、整体代换法.
3.常见误区:求值时注意α的范围,如果无法确定,一定要对α所在的象限进行分类讨论.
随堂演练
1
2
3
4
√
√
1
2
3
4
1
2
3
4
√
1
2
3
4
1
2
3
4
1
2
3
4
1
2
3
4
课时对点练
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
由条件知α是第四象限角,所以sin α<0,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
原式=sin2α+cos2α(cos2α+sin2α)
=sin2α+cos2α=1.
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为α为第二象限角,所以sin α>0,cos α<0,
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
由sin2α+cos2α=1,得1-cos2α=sin2α,
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
当x为第一象限角时,sin x>0,cos x>0,则f(x)=2+1=3,
当x为第二象限角时,sin x>0,cos x<0,则f(x)=2-1=1,
当x为第三象限角时,sin x<0,cos x<0,则f(x)=-2-1=-3,
当x为第四象限角时,sin x<0,cos x>0,则f(x)=-2+1=-1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.化简(1+tan215°)·cos215°= .
1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.设a>0且a≠1,若loga(sin x-cos x)=0,则sin8x+cos8x= .
1
因为a>0且a≠1,若loga(sin x-cos x)=0,
则sin x-cos x=a0=1,
所以(sin x-cos x)2=sin2x+cos2x-2sin xcos x=1,
又sin2x+cos2x=1,所以sin xcos x=0,
又由(sin2x+cos2x)2=sin4x+cos4x+2sin2x·cos2x=1,
得sin4x+cos4x=1,
所以sin8x+cos8x=(sin4x+cos4x)2-2sin4x·cos4x=(sin4x+cos4x)2=1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴α是第二或第三象限角.
当α是第二象限角时,则
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为α是第二象限角,
所以sin α>0,cos α<0.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∵α是第二象限角,且tan α=m,
∴m<0,sin α>0,cos α<0,mcos α=sin α,
代入平方关系得到m2cos2α+cos2α=1,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
8
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解得m=8.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)任取一个α的值,分别计算sin4α-cos4α,sin2α-cos2α,你又有什么发现?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(3)证明: x∈R,sin2x-cos2x=sin4x-cos4x.
对于任意实数x,都有sin2x-cos2x=(sin2x-cos2x)·(sin2x+cos2x)=sin4x-cos4x.
本课结束
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
