13.3.1等腰三角形(第2课时) 课件(共24张PPT)
文档属性
| 名称 | 13.3.1等腰三角形(第2课时) 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 664.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-27 21:08:34 | ||
图片预览



文档简介
(共24张PPT)
人教版七年级数学上册
13.4 等腰三角形
(第2课时)
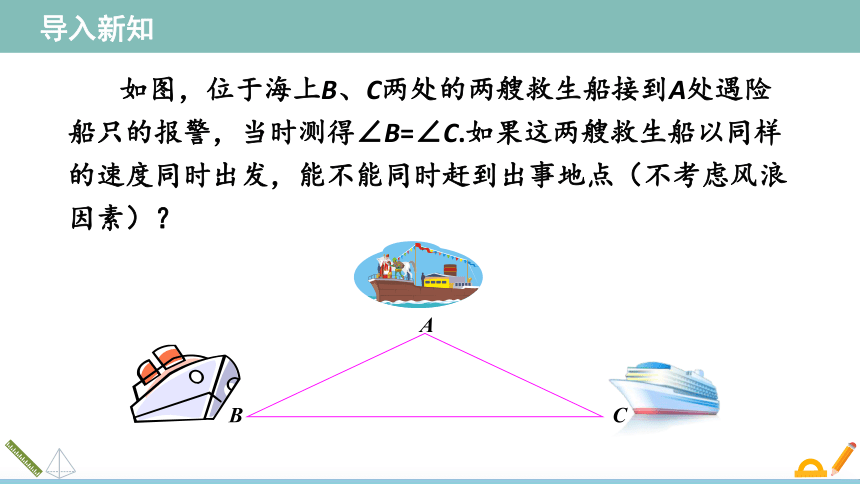
A
B
C
如图,位于海上B、C两处的两艘救生船接到A处遇险船只的报警,当时测得∠B=∠C.如果这两艘救生船以同样的速度同时出发,能不能同时赶到出事地点(不考虑风浪因素)?
导入新知
1.掌握等腰三角形的判定方法,并运用其进行证明和计算.
2.通过学习等腰三角形的判定方法,使学生能从正反两个方面认识等腰三角形,养成科学的思维习惯.
学习素养
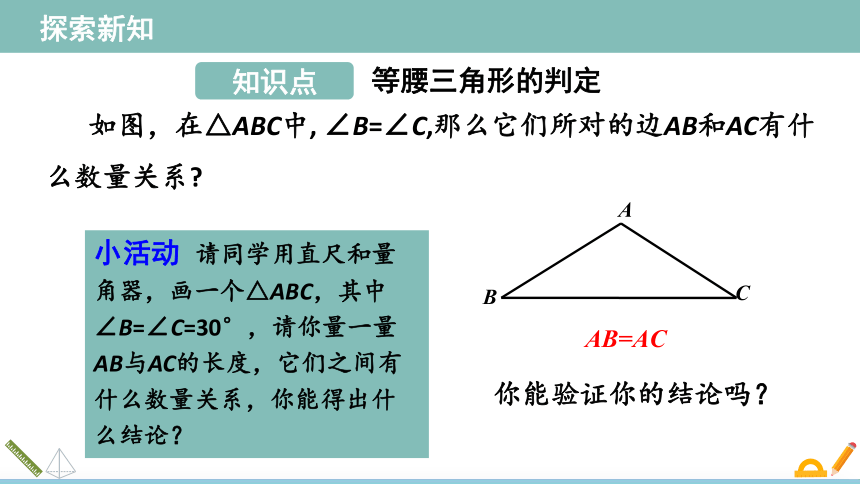
如图,在△ABC中, ∠B=∠C,那么它们所对的边AB和AC有什么数量关系
C
A
B
请同学用直尺和量角器,画一个△ABC,其中∠B=∠C=30°,请你量一量AB与AC的长度,它们之间有什么数量关系,你能得出什么结论?
AB=AC
你能验证你的结论吗?
小活动
等腰三角形的判定
知识点
探索新知
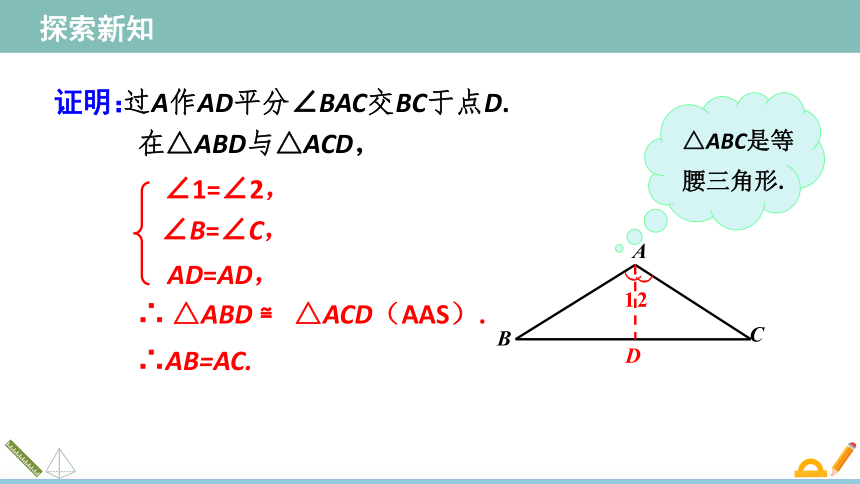
在△ABD与△ACD,
∠1=∠2,
∴ △ABD ≌ △ACD(AAS).
∠B=∠C,
AD=AD,
∴AB=AC.
过A作AD平分∠BAC交BC于点D.
证明:
C
A
B
2
1
D
(
(
△ABC是等腰三角形.
探索新知
∴ AC=AB. ( )
即△ABC为等腰三角形.
∵∠B=∠C, ( )
等腰三角形的判定方法:
如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”,这又是一个判定两条线段相等的根据之一).
已知
等角对等边
在△ABC中,
B
C
A
(
(
归纳总结
应用格式:
探索新知
A
B
C
D
2
1
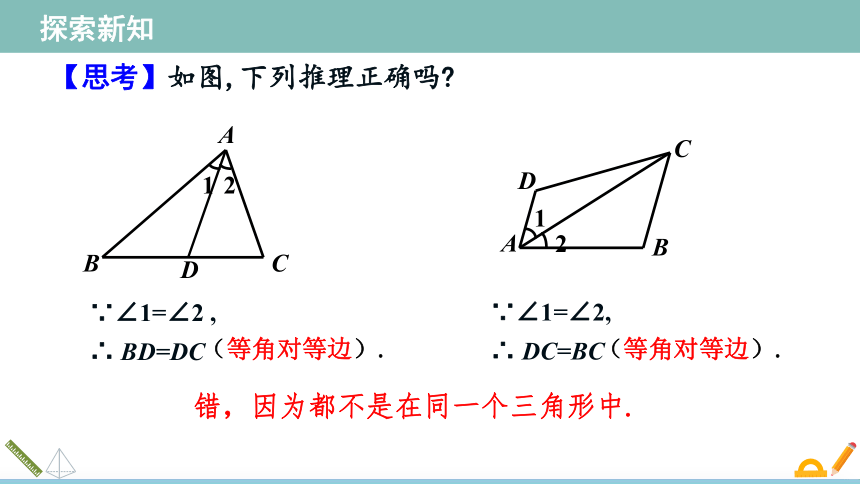
∵∠1=∠2 , ∴ BD=DC
(等角对等边).
∵∠1=∠2, ∴ DC=BC
A
B
C
D
2
1
(等角对等边).
错,因为都不是在同一个三角形中.
【思考】如图,下列推理正确吗
探索新知
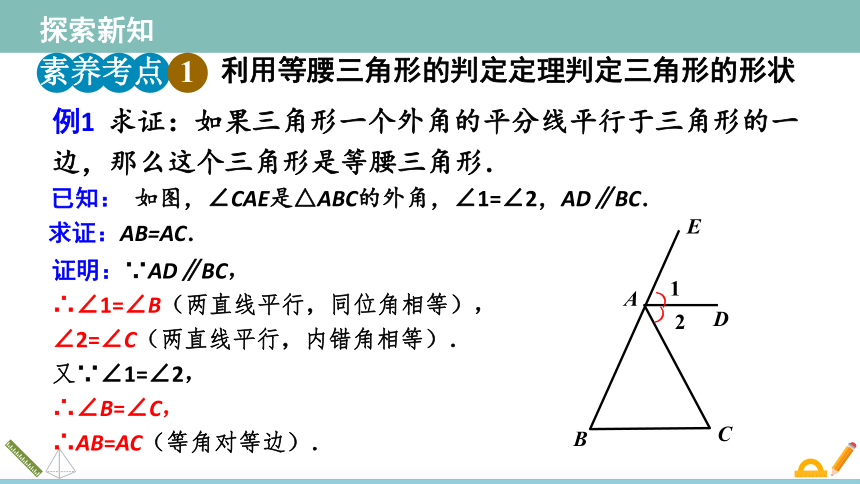
例1 求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
已知: 如图,∠CAE是△ABC的外角,∠1=∠2,AD∥BC.
求证:AB=AC.
证明:∵AD∥BC,
∴∠1=∠B(两直线平行,同位角相等),
∠2=∠C(两直线平行,内错角相等).
又∵∠1=∠2,
∴∠B=∠C,
∴AB=AC(等角对等边).
A
B
C
E
(
(
1
2
D
利用等腰三角形的判定定理判定三角形的形状
素养考点 1
探索新知
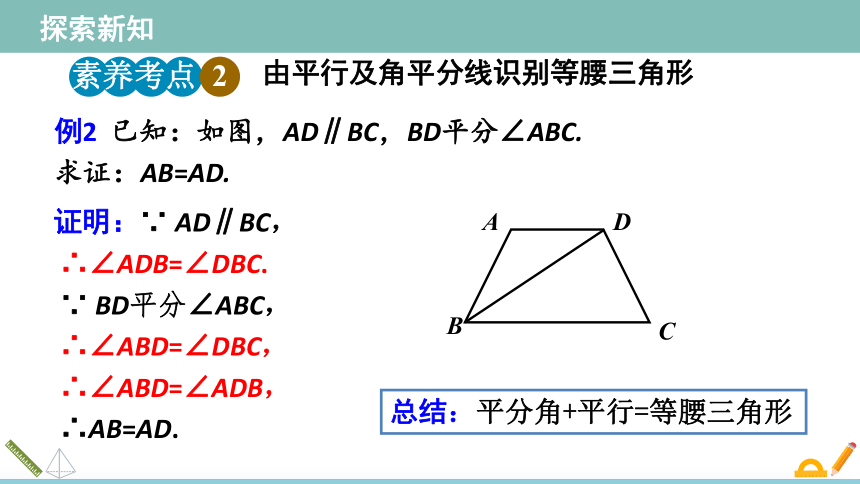
例2 已知:如图,AD∥BC,BD平分∠ABC.
求证:AB=AD.
B
A
D
C
证明:∵ AD∥BC,
∴∠ADB=∠DBC.
∵ BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABD=∠ADB,
∴AB=AD.
总结:平分角+平行=等腰三角形
由平行及角平分线识别等腰三角形
素养考点 2
探索新知
如图,已知OC平分∠AOB,CD∥OB,若OD=3cm,则CD等于_______.
3cm
如图,把一张长方形的纸沿着对角线折叠,重合部分是一个等腰三角形吗?为什么?
B
C
A
D
E
答:是.
由折叠可知,∠EBD=∠CBD.
∵AD∥BC,
∴∠EDB=∠EBD,
∴BE=DE,△EBD是等腰三角形.
∴∠EDB=∠CBD,
探索新知
例3 如图,在△ABC中,∠ACB=90°,CD是AB边上的高,AE是∠BAC的平分线,AE与CD交于点F,求证:△CEF是等腰三角形.
证明:∵在△ABC中,∠ACB=90°,
∴∠B+∠BAC=90°.
∵CD是AB边上的高,∴∠ACD+∠BAC=90°,
∴∠B=∠ACD.
∵AE是∠BAC的平分线,∴∠BAE=∠EAC,
∴∠B+∠BAE=∠ACD+∠EAC,即∠CEF=∠CFE,
∴CE=CF,∴△CEF是等腰三角形.
通过计算角相等来证明等腰三角形
素养考点 3
探索新知
“等角对等边”是判定等腰三角形的重要依据,它的前提条件是“在同一个三角形中”.
探索新知
如图所示,在△ABC中,AB=AC,点D,E在BC边上,∠ABD=
∠DAE=∠EAC=36°,则图中共有等腰三角形的个数是 ( )
A.4 B.5 C.6 D.7
C
解析: ∵AB=AC,∠ABC=36°,
∴∠BAC=108°,∴∠BAD=∠DAE=∠EAC=36°,
∴等腰三角形有△ABC,△ABD,△ADE,△ACE,△ACD,△ABE,共有6个.
探索新知
例4 已知等腰三角形底边长为a,底边上的高的长为h,求作等腰△ABC.使底边BC=a,底边上的高为h.
a
h
作法:
1.作线段AB=a.
2.作线段AB的垂直平分线MN,交AB 于点D.
3.在MN上取一点C,使DC=h.
4.连接AC,BC,则△ABC即为所求.
A
B
C
M
N
D
利用尺规作图作等腰三角形
素养考点 4
探索新知
例5 如图,在△ABC中,AB=AC,∠ABC和∠ACB的平分线交于点O.过O作EF∥BC交AB于E,交AC于F.
探究EF,BE,FC之间的关系.
O
A
B
C
E
F
解:EF=BE+CF.
理由如下:∵ EF∥BC,
∴∠EOB=∠CBO,∠FOC=∠BCO.
∵ BO,CO分别平分∠ABC,∠ACB,
∴∠CBO=∠ABO,∠BCO=∠ACO,
∴∠EOB=∠ABO ,∠FOC=∠ACO,
∴BE=OE,CF=OF,
∴ EF=EO+FO=BE+CF.
A
B
C
O
E
F
若AB≠AC,其他条件不变,图中还有等腰三角形吗?结论还成立吗?
利用等腰三角形的判定证明线段之间的关系
素养考点 5
探索新知
判定线段之间的数量关系,一般做法是通过证明线段所在的两个三角形全等或利用同一个三角形中“等角对等边”,运用转化思想,解决问题.
探索新知
∴MN=
O
A
B
C
M
N
1
2
3
4
5
6
在ΔABC中,OB平分∠ABC, OC平分∠ACB,过O点作MN ∥BC.
ΔAMN的周长=AB+AC吗?为什么?
∴ ΔAMN的周长=
AM+MN+AN
BM+CN.
= AM+BM+CN
+AN
=AB
+AC.
解:∵ OB平分∠ABC,∴∠1=∠2,
又 ∵MN∥BC,∴∠2=∠3,∴∠1=∠3.
∴OM=BM.同理得:ON=CN.
∵ MN=
OM+ON,
探索新知
在Rt△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACD交AB于E,则下列结论一定成立的是( )
A.BC=EC B.EC=BE C.BC=BE D.AE=EC
解析:∵∠ACB=90°,CD⊥AB,
∴∠ACD+∠BCD=90°,∠ACD+∠A=90°,
∴∠BCD=∠A.
∵CE平分∠ACD,
∴∠ACE=∠DCE.
又∵∠BEC=∠A+∠ACE,∠BCE=∠BCD+∠DCE,
∴∠BEC=∠BCE,
∴BC=BE.
C
探索新知
1.如图,在△ABC中,AB=AC,∠A=36°,BD,CE分别是∠ABC,∠BCD的角平分线,则图中的等腰三角形有( )
A.5个 B.4个 C.3个 D.2个
2.一个三角形的一个外角为130°,且它恰好等于一个不相邻的内角的2倍.这个三角形是( )
A.钝角三角形 B.直角三角形
C.等腰三角形 D.等边三角形
C
A
巩固练习
3.如图,直线a、b相交于点O,∠1=50°,点A在直线a上,直线b上存在点B,使以点O、A、B为顶点的三角形是等腰三角形,这样的B点有( )
A.1个 B.2个
C.3个 D.4个
D
1
O
a
b
A
巩固练习
4.如图,已知∠A=36°,∠DBC=36°,∠C=72°,则∠DBC=_____,∠BDC=_____,图中的等腰三角形有_______________________.
36°
72°
△ABC、
△DBA、
△BCD
5.如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为_____.
9
第5题图
A
B
C
D
第4题图
巩固练习
6.如图,上午10 时,一条船从A处出发以20海里每小时的速度向正北航行,中午12时到达B处,从A、B望灯塔C,测得∠NAC=40°,∠NBC=80°.求从B处到灯塔C的距离.
解:∵∠NBC=∠A+∠C,
∴∠C=80°– 40°= 40°,
∴ ∠C = ∠A,∴ BA=BC(等角对等边).
∵AB=20×(12–10)=40(海里),
∴BC=40海里.
答:B处距离灯塔C为40海里.
80°
40°
N
B
A
C
北
巩固练习
等腰三角形的判定
等角对等边
定义
注意是指同一个三角形中
有两边相等的三角形是等腰三角形
课堂小结
谢 谢
人教版七年级数学上册
13.4 等腰三角形
(第2课时)
A
B
C
如图,位于海上B、C两处的两艘救生船接到A处遇险船只的报警,当时测得∠B=∠C.如果这两艘救生船以同样的速度同时出发,能不能同时赶到出事地点(不考虑风浪因素)?
导入新知
1.掌握等腰三角形的判定方法,并运用其进行证明和计算.
2.通过学习等腰三角形的判定方法,使学生能从正反两个方面认识等腰三角形,养成科学的思维习惯.
学习素养
如图,在△ABC中, ∠B=∠C,那么它们所对的边AB和AC有什么数量关系
C
A
B
请同学用直尺和量角器,画一个△ABC,其中∠B=∠C=30°,请你量一量AB与AC的长度,它们之间有什么数量关系,你能得出什么结论?
AB=AC
你能验证你的结论吗?
小活动
等腰三角形的判定
知识点
探索新知
在△ABD与△ACD,
∠1=∠2,
∴ △ABD ≌ △ACD(AAS).
∠B=∠C,
AD=AD,
∴AB=AC.
过A作AD平分∠BAC交BC于点D.
证明:
C
A
B
2
1
D
(
(
△ABC是等腰三角形.
探索新知
∴ AC=AB. ( )
即△ABC为等腰三角形.
∵∠B=∠C, ( )
等腰三角形的判定方法:
如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”,这又是一个判定两条线段相等的根据之一).
已知
等角对等边
在△ABC中,
B
C
A
(
(
归纳总结
应用格式:
探索新知
A
B
C
D
2
1
∵∠1=∠2 , ∴ BD=DC
(等角对等边).
∵∠1=∠2, ∴ DC=BC
A
B
C
D
2
1
(等角对等边).
错,因为都不是在同一个三角形中.
【思考】如图,下列推理正确吗
探索新知
例1 求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
已知: 如图,∠CAE是△ABC的外角,∠1=∠2,AD∥BC.
求证:AB=AC.
证明:∵AD∥BC,
∴∠1=∠B(两直线平行,同位角相等),
∠2=∠C(两直线平行,内错角相等).
又∵∠1=∠2,
∴∠B=∠C,
∴AB=AC(等角对等边).
A
B
C
E
(
(
1
2
D
利用等腰三角形的判定定理判定三角形的形状
素养考点 1
探索新知
例2 已知:如图,AD∥BC,BD平分∠ABC.
求证:AB=AD.
B
A
D
C
证明:∵ AD∥BC,
∴∠ADB=∠DBC.
∵ BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABD=∠ADB,
∴AB=AD.
总结:平分角+平行=等腰三角形
由平行及角平分线识别等腰三角形
素养考点 2
探索新知
如图,已知OC平分∠AOB,CD∥OB,若OD=3cm,则CD等于_______.
3cm
如图,把一张长方形的纸沿着对角线折叠,重合部分是一个等腰三角形吗?为什么?
B
C
A
D
E
答:是.
由折叠可知,∠EBD=∠CBD.
∵AD∥BC,
∴∠EDB=∠EBD,
∴BE=DE,△EBD是等腰三角形.
∴∠EDB=∠CBD,
探索新知
例3 如图,在△ABC中,∠ACB=90°,CD是AB边上的高,AE是∠BAC的平分线,AE与CD交于点F,求证:△CEF是等腰三角形.
证明:∵在△ABC中,∠ACB=90°,
∴∠B+∠BAC=90°.
∵CD是AB边上的高,∴∠ACD+∠BAC=90°,
∴∠B=∠ACD.
∵AE是∠BAC的平分线,∴∠BAE=∠EAC,
∴∠B+∠BAE=∠ACD+∠EAC,即∠CEF=∠CFE,
∴CE=CF,∴△CEF是等腰三角形.
通过计算角相等来证明等腰三角形
素养考点 3
探索新知
“等角对等边”是判定等腰三角形的重要依据,它的前提条件是“在同一个三角形中”.
探索新知
如图所示,在△ABC中,AB=AC,点D,E在BC边上,∠ABD=
∠DAE=∠EAC=36°,则图中共有等腰三角形的个数是 ( )
A.4 B.5 C.6 D.7
C
解析: ∵AB=AC,∠ABC=36°,
∴∠BAC=108°,∴∠BAD=∠DAE=∠EAC=36°,
∴等腰三角形有△ABC,△ABD,△ADE,△ACE,△ACD,△ABE,共有6个.
探索新知
例4 已知等腰三角形底边长为a,底边上的高的长为h,求作等腰△ABC.使底边BC=a,底边上的高为h.
a
h
作法:
1.作线段AB=a.
2.作线段AB的垂直平分线MN,交AB 于点D.
3.在MN上取一点C,使DC=h.
4.连接AC,BC,则△ABC即为所求.
A
B
C
M
N
D
利用尺规作图作等腰三角形
素养考点 4
探索新知
例5 如图,在△ABC中,AB=AC,∠ABC和∠ACB的平分线交于点O.过O作EF∥BC交AB于E,交AC于F.
探究EF,BE,FC之间的关系.
O
A
B
C
E
F
解:EF=BE+CF.
理由如下:∵ EF∥BC,
∴∠EOB=∠CBO,∠FOC=∠BCO.
∵ BO,CO分别平分∠ABC,∠ACB,
∴∠CBO=∠ABO,∠BCO=∠ACO,
∴∠EOB=∠ABO ,∠FOC=∠ACO,
∴BE=OE,CF=OF,
∴ EF=EO+FO=BE+CF.
A
B
C
O
E
F
若AB≠AC,其他条件不变,图中还有等腰三角形吗?结论还成立吗?
利用等腰三角形的判定证明线段之间的关系
素养考点 5
探索新知
判定线段之间的数量关系,一般做法是通过证明线段所在的两个三角形全等或利用同一个三角形中“等角对等边”,运用转化思想,解决问题.
探索新知
∴MN=
O
A
B
C
M
N
1
2
3
4
5
6
在ΔABC中,OB平分∠ABC, OC平分∠ACB,过O点作MN ∥BC.
ΔAMN的周长=AB+AC吗?为什么?
∴ ΔAMN的周长=
AM+MN+AN
BM+CN.
= AM+BM+CN
+AN
=AB
+AC.
解:∵ OB平分∠ABC,∴∠1=∠2,
又 ∵MN∥BC,∴∠2=∠3,∴∠1=∠3.
∴OM=BM.同理得:ON=CN.
∵ MN=
OM+ON,
探索新知
在Rt△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACD交AB于E,则下列结论一定成立的是( )
A.BC=EC B.EC=BE C.BC=BE D.AE=EC
解析:∵∠ACB=90°,CD⊥AB,
∴∠ACD+∠BCD=90°,∠ACD+∠A=90°,
∴∠BCD=∠A.
∵CE平分∠ACD,
∴∠ACE=∠DCE.
又∵∠BEC=∠A+∠ACE,∠BCE=∠BCD+∠DCE,
∴∠BEC=∠BCE,
∴BC=BE.
C
探索新知
1.如图,在△ABC中,AB=AC,∠A=36°,BD,CE分别是∠ABC,∠BCD的角平分线,则图中的等腰三角形有( )
A.5个 B.4个 C.3个 D.2个
2.一个三角形的一个外角为130°,且它恰好等于一个不相邻的内角的2倍.这个三角形是( )
A.钝角三角形 B.直角三角形
C.等腰三角形 D.等边三角形
C
A
巩固练习
3.如图,直线a、b相交于点O,∠1=50°,点A在直线a上,直线b上存在点B,使以点O、A、B为顶点的三角形是等腰三角形,这样的B点有( )
A.1个 B.2个
C.3个 D.4个
D
1
O
a
b
A
巩固练习
4.如图,已知∠A=36°,∠DBC=36°,∠C=72°,则∠DBC=_____,∠BDC=_____,图中的等腰三角形有_______________________.
36°
72°
△ABC、
△DBA、
△BCD
5.如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为_____.
9
第5题图
A
B
C
D
第4题图
巩固练习
6.如图,上午10 时,一条船从A处出发以20海里每小时的速度向正北航行,中午12时到达B处,从A、B望灯塔C,测得∠NAC=40°,∠NBC=80°.求从B处到灯塔C的距离.
解:∵∠NBC=∠A+∠C,
∴∠C=80°– 40°= 40°,
∴ ∠C = ∠A,∴ BA=BC(等角对等边).
∵AB=20×(12–10)=40(海里),
∴BC=40海里.
答:B处距离灯塔C为40海里.
80°
40°
N
B
A
C
北
巩固练习
等腰三角形的判定
等角对等边
定义
注意是指同一个三角形中
有两边相等的三角形是等腰三角形
课堂小结
谢 谢
