1.5.1三角形的中位线

课件23张PPT。三角形的中位线前测已知：如图， ABCD中，E、F分别是AD、BC上的两点，且AE=FC
求证：四边形EBFD是平行四边形证明：
∵四边形ABCD为平行四边形
∴AD//BC 即 ED//BF
AD=BC
又∵AE=FC
∴AD-AE=BC-FC 即ED=BF
∵ ED//BF
∴四边形EBFD是平行四边形示标1、理解三角形中位线的概念，掌握它的性质
2、能较熟练地应用三角形中位线性质进行有关的证明和计算．
3、经历探索、猜想、证明的过程，进一步发展推理论证的能力．
学习重点：掌握和运用三角形中位线的性质．
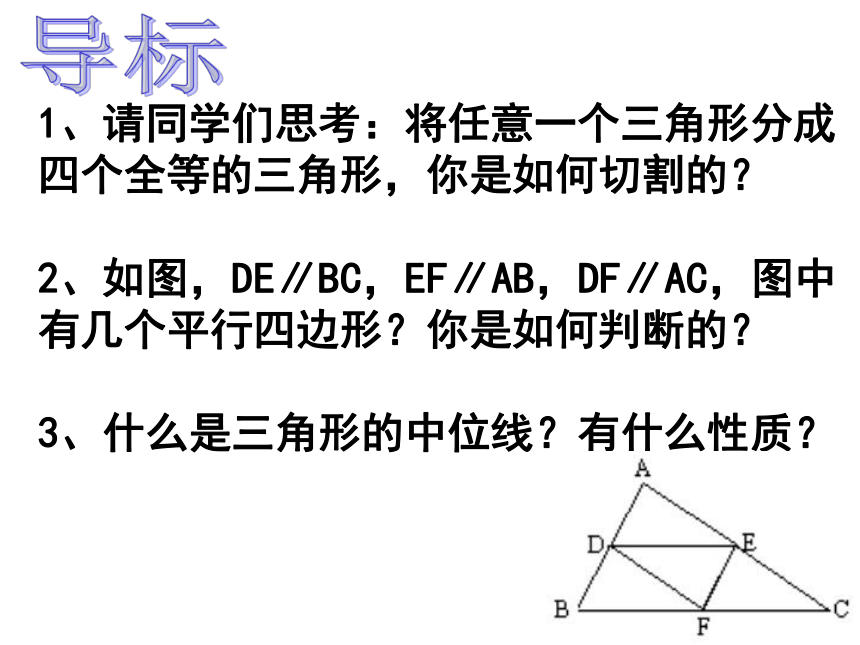
学习难点：三角形中位线性质的证明（辅助线的添加方法）．导标1、请同学们思考：将任意一个三角形分成四个全等的三角形，你是如何切割的？
2、如图，DE∥BC，EF∥AB，DF∥AC，图中有几个平行四边形？你是如何判断的？
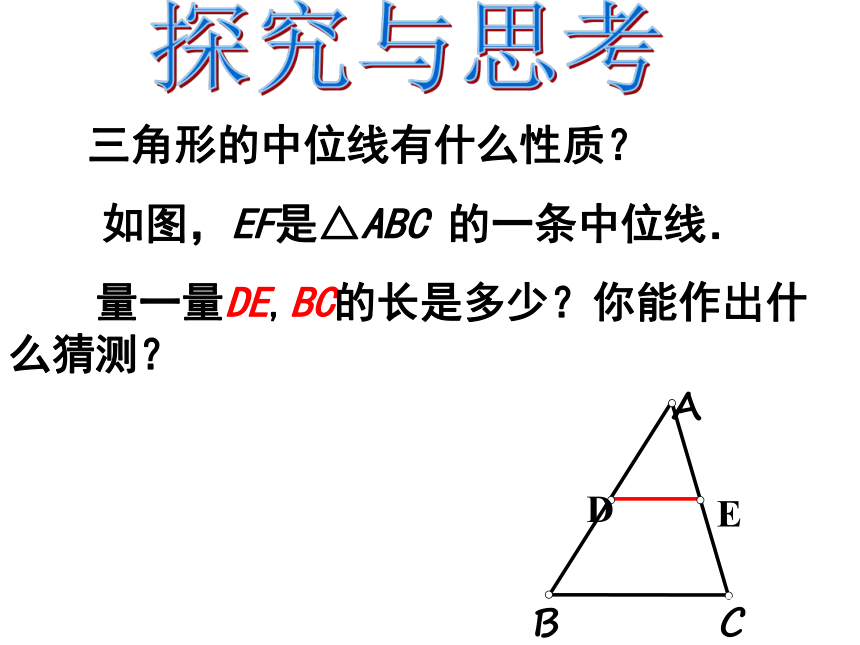
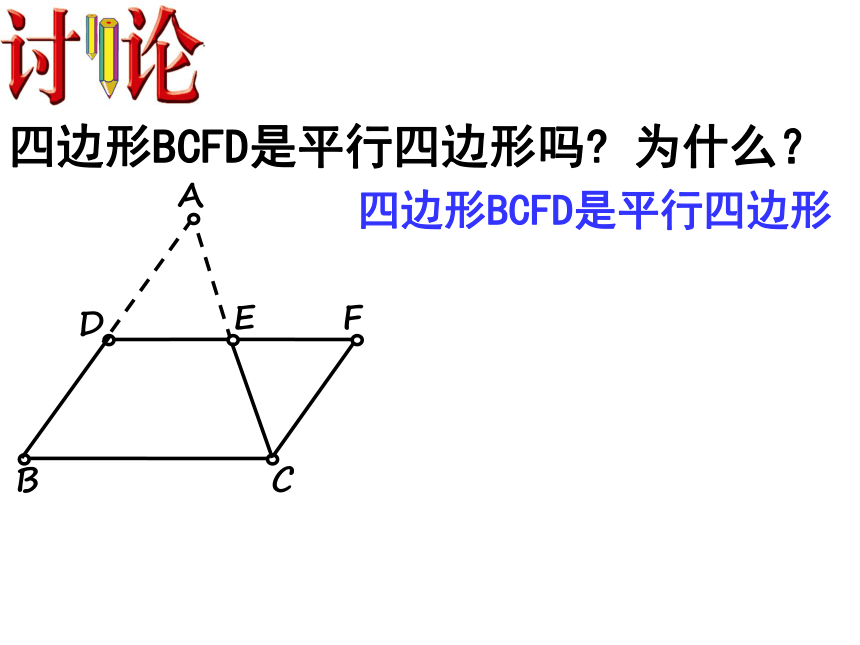
3、什么是三角形的中位线？有什么性质？三角形的中位线有什么性质？如图，EF是△ABC 的一条中位线． 量一量DE,BC的长是多少？你能作出什么猜测？探究与思考怎样将一个三角形纸片剪成两部分，使分成的两部分能拼成一个平行四边形？(1)剪一个三角形,记为△ABC;(2)沿中位线DE将△ABC剪成两部分,并将△ADE绕点E顺时针旋转180°得四边形BCFD. ABCDEF四边形BCFD是平行四边形吗? 为什么？四边形BCFD是平行四边形ABCEDF三角形中位线定义：
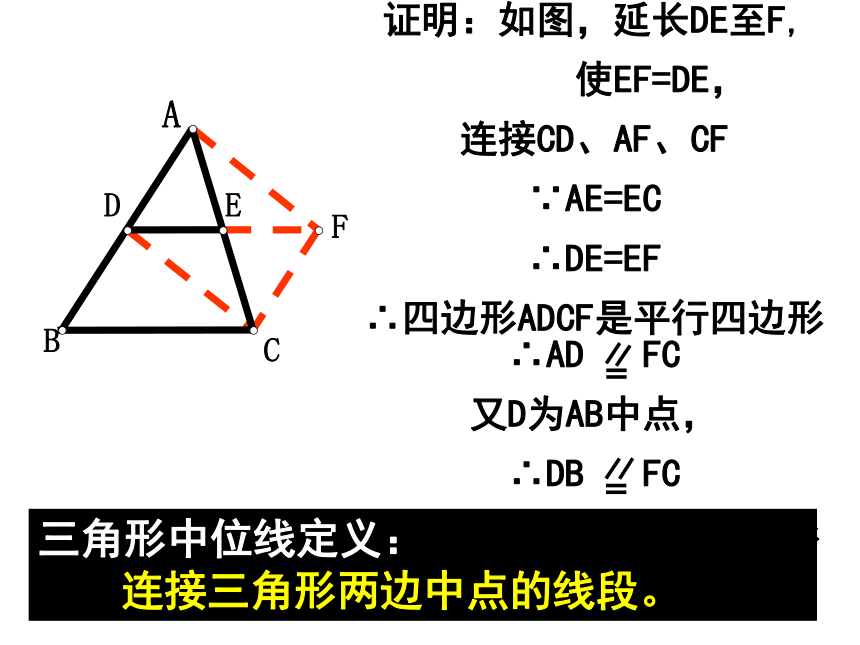
连接三角形两边中点的线段。
3． 想一想：
（1）①一个三角形的中位线共有几条？
②三角形的中位线与中线有什么区别？

（2）三角形的中位线与第三边有怎样的关系？
想一想！3条中位线是任意两边中点的连线
中线是顶点与对边中点的连线
三角形中位线定理
三角形的中位线平行于第三边，且等于第三边的一半。 用符号语言表示∵DE是△ABC的中位线
∴ DE∥BC，
DE= BC.数量关系位置关系(1)证明平行
(2)证明一条线段是另一条线
段的2倍或ABCDE 三角形的中位线定理:三角形的中位线平行于第三边，并且等于第三边的一半.三角形的中位线定理的主要用途：已知：如图，在四边形ABCD中，E、F、G、H分别是AB、BC、CD、DA的中点。
求证：四边形EFGH是平行四边形。挑战自我合作探究测标1．如图，A、B两点被池塘隔开，在AB外选一点C，连结AC和BC，并分别找出AC和BC的中点M、N，如果测得MN=20 m，那么A、B两点的距离是 m，理由是 ___ ．40三角形的中位线平行于第三边，并且等于第三边的一半已知：△ABC的各边分别为AB=8cm 、AC=10cm和BC=12cm ，且点D、E、F为AB、AC、BC的中点，
求：△DEF的周长．
解：∵AD=BD，AE=EC
∴DE= BC = ×12=6
同理可得：DF= AC= ×10=5
EF= AB= ×8=4
∴C△DEF=DE+DF+EF
=6+5+4=15 (cm)固标1、什么是三角形的中位线？
2、如何运用三角形的中位线？
注意什么问题？谢谢~！作业：一课三练谢谢大家巩固新知
１.三角形的中位线_______第三边,并且______第三边的____________
2．如图：在△ABC中，DE是中位线。
（1）若∠ADE=60°，则∠B= ;
（2）若BC=8cm，则DE= cm.
（3）DE +BC=12cm,则BC=——
3．若等腰△ABC的周长是40cm,AB=AC=14cm,则中位线DE＝———60°4ABCDED 8cm６cm　　　　　　　　　　　　平行于　　　　　　　　　
　等于　　　　　　　　一半　　　　　　　　4.如图, MN 为△ABC 的中位线,若∠ABC =61°则∠AMN = ,
若MN =12 ,则BC = . 61°24 5. 如图, △ABC 中, D ,E 分别为AB,
AC 的中点,当BC =10㎝时,则DE = .5㎝ 6.如图,已知△ABC中,
AB = 3㎝,BC=3.4 ㎝ AC=4㎝ 且D,E,F分别为 AB,BC,AC边的中点,则△DEF的周长
是 ㎝.
5.27、如下图：在Rt △ ABC中，∠A=90°,D、E、F分别是各边中点, AB=6cm，AC=8cm，则△DEF的周长= cm。12EFBACD 知识总结：
1。判定定理：一组对边平行且相等的四边形是平行四边形
2.定义 ：连接三角形两边中点的线段叫做三角形的中位线
3.三角形的中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半。数学思想：转化思想
1.把四边形的问题转化为三角形问题解决
2.线段的倍分问题可转化为相等问题来解决.
数学方法：在三角形的中位线定理的发现过程用到画图、测量、猜想、验证、证明等数学方法本节课你有哪些收获？