1.5.1 第1课时 乘方 课件(共20页)
文档属性
| 名称 | 1.5.1 第1课时 乘方 课件(共20页) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-27 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
1.5.1 乘 方
第一章 有理数
第1课时 乘 方
人教版 七年级上
精品同步教学课件
问题 某种细胞每1小时便由一个分裂成两个.经过6小时这种细胞由1个能分裂成多少个?
乘方的意义
一
问题引导
第一次
第二次
第三次
分裂方式如下所示:
这个细胞分裂一次可得多少个细胞
那么,6小时共分裂了多少次 有多少个细胞?
解:一次得:
两次:
三次:
四次:
2个;
2×2个;
2×2×2个;
六次: 2×2×2×2×2×2个.
分裂两次呢
分裂三次呢 四次呢?
思考:
2×2×2×2个
问题 这两个式子有什么相同点
它们都是乘法;并且它们各自的因数都相同.
思考 同学们想一想:这样的运算能像平方、立方那样简写吗?
请比较细胞分裂四次后的个数式子:2×2×2×2
和细胞分裂六次后的个数式子: 2×2×2×2×2×2.
例如:2×2×2×2
2×2×2×2×2×2
记作
记作
知识要点
一般地,n个相同的因数a相乘,记作an,读作“a的n次幂(或a的n次方)”,即
a·a·a· ·a = an
n个
…
读作2的6次方(幂).
读作2的4次方(幂).
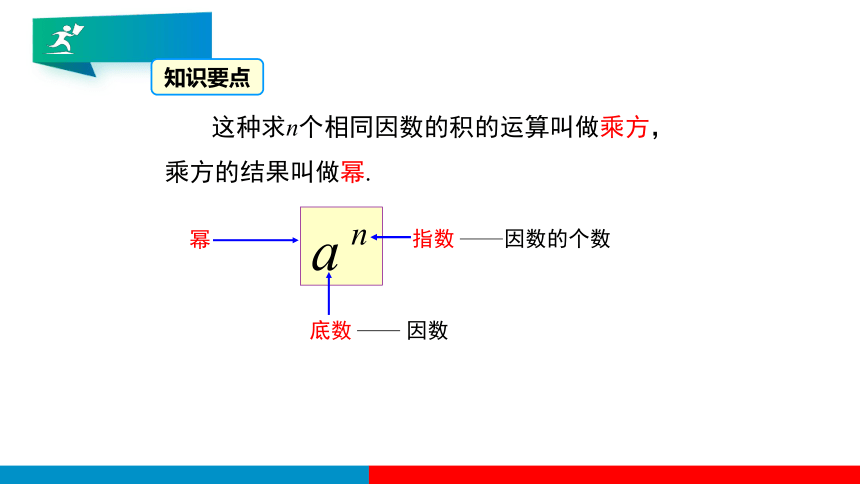
这种求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂.
幂
指数
因数的个数
底数
因数
知识要点
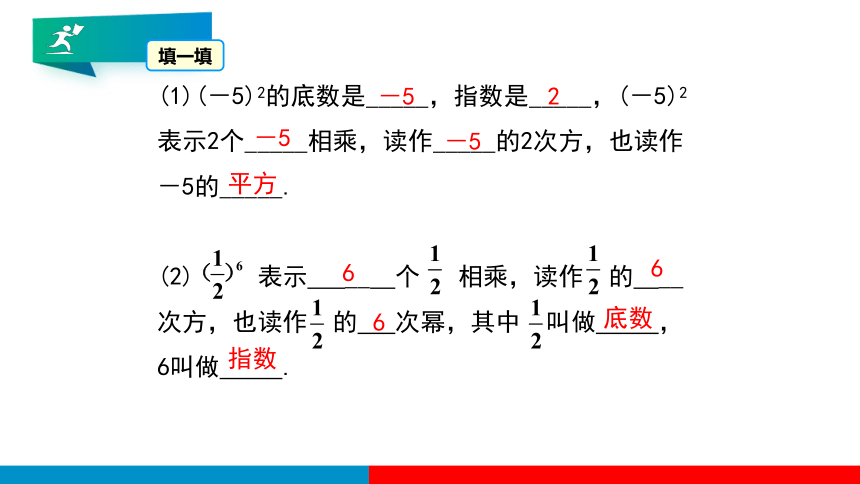
(1)(-5)2的底数是_____,指数是_____,(-5)2表示2个_____相乘,读作_____的2次方,也读作-5的_____.
(2) 表示 __ 个 相乘,读作 的 __ 次方,也读作 的 次幂,其中 叫做 ,6叫做 .
填一填
-5
2
-5
-5
平方
6
6
6
底数
指数
练习
填空:
(1)(-2)5 的底数是______,指数是______,它表示________________________________.
(2)-25 的底数是______ ,指数是______ ,它表示_________________.
(3)的底数是______ ,指数是______ ,它表示______________.
-2
5
(-2)×(-2)×(-2)×(-2)×(-2)
2
5
-2×2×2×2×2
-
2
×
练习:把下列各式写成乘方运算的形式,并指出底数,指数各是什么
1. 5×5×5×5×5
2. (-1.3)(-1.3)(-1.3)(-1.3)
4. m·m ·m ·… ·m
2a个
例1 计算:
(1) (-4)3; (2) (-2)4; (3)
解:(1) (-4)3=(-4)×(-4)×(-4)=-64;
(2) (-2)4=(-2)×(-2)×(-2)×(-2)=16;
思考:你发现负数的幂的正负有什么规律?
归纳总结
1.负数的奇次幂是负数,负数的偶次幂是正数.
2.正数的任何正整数次幂都是正数,0的任何正整数次幂都是0.
根据有理数的乘法法则可以得出:
(-4)2与-42
观察下面两个式子有什么不同?
(-4)2表示-4的平方,-42表示4的平方的相反数.
议一议
(-4)2与-42 互为相反数
当堂练习
1.填空:
(1)-(-3)2= ; (2)-32= ;
(3)(-5)3= ; (4)0.13= ;
(5)(-1)9= ; (6)(-1)12= ;
(7)(-1)2n= ; (8)(-1)2n+1= ;
(9)(-1)n= .
-9
-9
-125
0.001
-1
1
1
-1
(当n为奇数时)
(当n为偶数时)
2
计算:
(1)(-5)4;(2)-54;(3)3;
(4)3;(5)(-1)2 024.
解题秘方:将乘方运算转化为乘法运算算出结果.
解:(1)(-5)4=(-5)×(-5)×(-5)×(-5) = 625.
(2)-54=-(5×5×5×5)=-625.
(3)3 = ×× = .
(4) 3 = ×× =- .
(5)(-1)2 024=(-1)×(-1)×(-1)×…×(-1)
=1.
2024个
-1的偶次幂等于1,奇次幂等于-1.
3. 计算:
(1)2;
(2)(-0.1)4;
(3)3;
(4)-.
原式=0.0001;
1.求几个相同因数的积的运算,叫做乘方.
2.乘方的符号法则:
(1)正数的任何次幂都是正数
(2)负数的奇次幂是负数,负数的偶次幂是正数
(3)零的正整数次幂都是零
课堂小结
幂
指数
底数
https://www.21cnjy.com/help/help_extract.php
1.5.1 乘 方
第一章 有理数
第1课时 乘 方
人教版 七年级上
精品同步教学课件
问题 某种细胞每1小时便由一个分裂成两个.经过6小时这种细胞由1个能分裂成多少个?
乘方的意义
一
问题引导
第一次
第二次
第三次
分裂方式如下所示:
这个细胞分裂一次可得多少个细胞
那么,6小时共分裂了多少次 有多少个细胞?
解:一次得:
两次:
三次:
四次:
2个;
2×2个;
2×2×2个;
六次: 2×2×2×2×2×2个.
分裂两次呢
分裂三次呢 四次呢?
思考:
2×2×2×2个
问题 这两个式子有什么相同点
它们都是乘法;并且它们各自的因数都相同.
思考 同学们想一想:这样的运算能像平方、立方那样简写吗?
请比较细胞分裂四次后的个数式子:2×2×2×2
和细胞分裂六次后的个数式子: 2×2×2×2×2×2.
例如:2×2×2×2
2×2×2×2×2×2
记作
记作
知识要点
一般地,n个相同的因数a相乘,记作an,读作“a的n次幂(或a的n次方)”,即
a·a·a· ·a = an
n个
…
读作2的6次方(幂).
读作2的4次方(幂).
这种求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂.
幂
指数
因数的个数
底数
因数
知识要点
(1)(-5)2的底数是_____,指数是_____,(-5)2表示2个_____相乘,读作_____的2次方,也读作-5的_____.
(2) 表示 __ 个 相乘,读作 的 __ 次方,也读作 的 次幂,其中 叫做 ,6叫做 .
填一填
-5
2
-5
-5
平方
6
6
6
底数
指数
练习
填空:
(1)(-2)5 的底数是______,指数是______,它表示________________________________.
(2)-25 的底数是______ ,指数是______ ,它表示_________________.
(3)的底数是______ ,指数是______ ,它表示______________.
-2
5
(-2)×(-2)×(-2)×(-2)×(-2)
2
5
-2×2×2×2×2
-
2
×
练习:把下列各式写成乘方运算的形式,并指出底数,指数各是什么
1. 5×5×5×5×5
2. (-1.3)(-1.3)(-1.3)(-1.3)
4. m·m ·m ·… ·m
2a个
例1 计算:
(1) (-4)3; (2) (-2)4; (3)
解:(1) (-4)3=(-4)×(-4)×(-4)=-64;
(2) (-2)4=(-2)×(-2)×(-2)×(-2)=16;
思考:你发现负数的幂的正负有什么规律?
归纳总结
1.负数的奇次幂是负数,负数的偶次幂是正数.
2.正数的任何正整数次幂都是正数,0的任何正整数次幂都是0.
根据有理数的乘法法则可以得出:
(-4)2与-42
观察下面两个式子有什么不同?
(-4)2表示-4的平方,-42表示4的平方的相反数.
议一议
(-4)2与-42 互为相反数
当堂练习
1.填空:
(1)-(-3)2= ; (2)-32= ;
(3)(-5)3= ; (4)0.13= ;
(5)(-1)9= ; (6)(-1)12= ;
(7)(-1)2n= ; (8)(-1)2n+1= ;
(9)(-1)n= .
-9
-9
-125
0.001
-1
1
1
-1
(当n为奇数时)
(当n为偶数时)
2
计算:
(1)(-5)4;(2)-54;(3)3;
(4)3;(5)(-1)2 024.
解题秘方:将乘方运算转化为乘法运算算出结果.
解:(1)(-5)4=(-5)×(-5)×(-5)×(-5) = 625.
(2)-54=-(5×5×5×5)=-625.
(3)3 = ×× = .
(4) 3 = ×× =- .
(5)(-1)2 024=(-1)×(-1)×(-1)×…×(-1)
=1.
2024个
-1的偶次幂等于1,奇次幂等于-1.
3. 计算:
(1)2;
(2)(-0.1)4;
(3)3;
(4)-.
原式=0.0001;
1.求几个相同因数的积的运算,叫做乘方.
2.乘方的符号法则:
(1)正数的任何次幂都是正数
(2)负数的奇次幂是负数,负数的偶次幂是正数
(3)零的正整数次幂都是零
课堂小结
幂
指数
底数
https://www.21cnjy.com/help/help_extract.php
