冀教版八年级上册12.3 12.3 分式的加减(第3课时) 课件(共27张PPT)
文档属性
| 名称 | 冀教版八年级上册12.3 12.3 分式的加减(第3课时) 课件(共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-27 19:57:42 | ||
图片预览



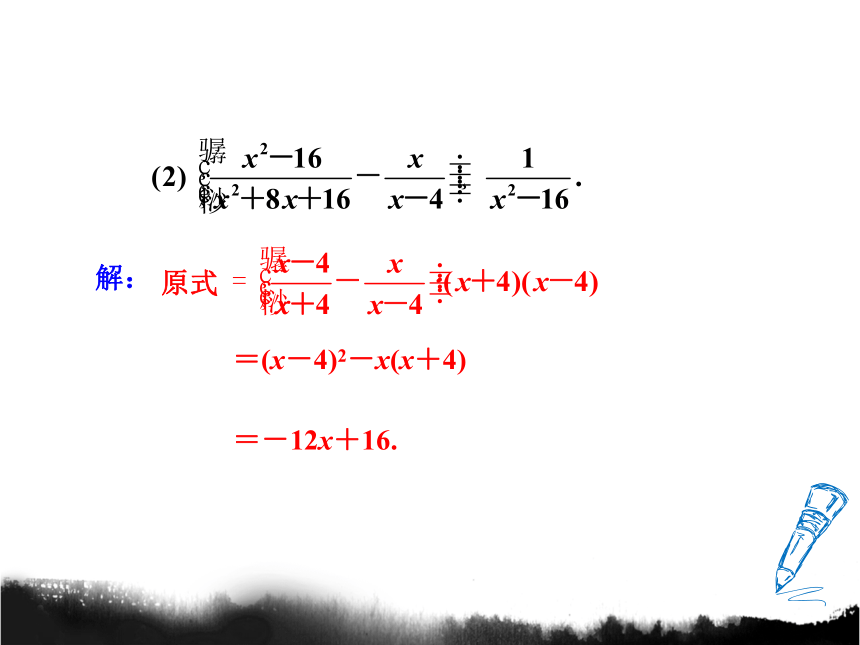





文档简介
(共27张PPT)
第十二章 分式和分式方程
第3课时 分式运算的常见
应用技巧
习题课
名师点金
有关分式化简求值的方法:
一般是先运用分式运算法则把分式化简为最简分式或整式,然后将已知的数值代入求值.技巧:
(1)如果所给的字母的取值比较复杂或是以条件等式的
形式给出时,一般考虑用整体代入法;
(2)当给的是几个量的比值时,采用设参数法或倒数法
等.
1
题型
按常规运算法则化简
1.
解:
原式
解:
原式
=(x-4)2-x(x+4)
=-12x+16.
2
按常规化简求值
题型
2. 【中考·盐城】先化简,再求值:
其中a=4.
解:
原式=
=
=
当a=4时,原式= =4.
3
分式化简的技巧
题型
3.计算:
技巧1
先分解,再化简
解:
原式=
=
4.化简:
技巧2
先用运算律,再化简
解:
原式=1·(x2-1)- ·(x2-1)
=(x2-1)-x(x+1)
=-1-x.
5.计算:
技巧3
先分组再通分
解:
原式=
=
=
=
=
多个分式相加减时,要先观察其特征,如果有同分母的,可以把同分母分式先加减;如果有同分子的,也可以把同分子的先加减.
方法总结:
6.计算:
技巧4
先约分,再通分
解:
原式=
=
=
直接通分,极其烦琐.通过观察,发现各个分式并非最简分式,可先化简,化简后再计算会简便许多.
点拨:
7.计算:
技巧5
先排序,再通分(逐项通分)
解:
原式=
=
=
此题若采用各项一起通分后再相加的方法,计算量较大,可逐项通分达到解题的目的.
点拨:
同类变式
8.计算:
技巧6
先分式分离,后通分
同类变式
9.计算:
技巧7
利用 解题
同类变式
10.计算:(3m-2n)+ -(3m-2n)2
+
技巧8
先换元,再化简
4
分式求值的技巧
11.【中考·毕节】已知A=(x-3)
(1)化简A;
(2)若x满足不等式组 且x为整数时,
求A的值.
题型
技巧9
条件法求值
解:
(1)A=
=
=
=
(2)
由①得:x<1,由②得:x>-1,
∴不等式组的解集为-1则A=-
12.【中考·齐齐哈尔】先化简,再求值:
其中x2+2x-15=0.
技巧10
整体法求值
解:
原式=
=
=
=
=
∵x2+2x-15=0,
∴x2+2x=15.
∴原式=
本题考查了分式的化简求值,解题关键是掌握分式的基本运算.先按照分式计算的顺序(先算乘除,再算加减)化简分式.再根据题目的需要,灵活运用条件x2+2x-15=0转化整体代入求值.
点拨:
同类变式
13.已知abc≠0且a+b+c=0,
求 的值.
技巧11
补项法求值
同类变式
14.阅读下面的解题过程:
已知: ,求 的值.
解:由 知x≠0,所以 =3,
即x+ =3.
技巧12
倒数法求值
所以 =32-2=7.
故 的值为 .
该题的解法叫做“倒数法”,请你利用“倒数法”解下面的题目:
已知 ,求 的值.
同类变式
15.已知4x-3y-6z=0,x+2y-7z=0,且xyz≠0,
求 的值.
技巧13
消元法求值
第十二章 分式和分式方程
第3课时 分式运算的常见
应用技巧
习题课
名师点金
有关分式化简求值的方法:
一般是先运用分式运算法则把分式化简为最简分式或整式,然后将已知的数值代入求值.技巧:
(1)如果所给的字母的取值比较复杂或是以条件等式的
形式给出时,一般考虑用整体代入法;
(2)当给的是几个量的比值时,采用设参数法或倒数法
等.
1
题型
按常规运算法则化简
1.
解:
原式
解:
原式
=(x-4)2-x(x+4)
=-12x+16.
2
按常规化简求值
题型
2. 【中考·盐城】先化简,再求值:
其中a=4.
解:
原式=
=
=
当a=4时,原式= =4.
3
分式化简的技巧
题型
3.计算:
技巧1
先分解,再化简
解:
原式=
=
4.化简:
技巧2
先用运算律,再化简
解:
原式=1·(x2-1)- ·(x2-1)
=(x2-1)-x(x+1)
=-1-x.
5.计算:
技巧3
先分组再通分
解:
原式=
=
=
=
=
多个分式相加减时,要先观察其特征,如果有同分母的,可以把同分母分式先加减;如果有同分子的,也可以把同分子的先加减.
方法总结:
6.计算:
技巧4
先约分,再通分
解:
原式=
=
=
直接通分,极其烦琐.通过观察,发现各个分式并非最简分式,可先化简,化简后再计算会简便许多.
点拨:
7.计算:
技巧5
先排序,再通分(逐项通分)
解:
原式=
=
=
此题若采用各项一起通分后再相加的方法,计算量较大,可逐项通分达到解题的目的.
点拨:
同类变式
8.计算:
技巧6
先分式分离,后通分
同类变式
9.计算:
技巧7
利用 解题
同类变式
10.计算:(3m-2n)+ -(3m-2n)2
+
技巧8
先换元,再化简
4
分式求值的技巧
11.【中考·毕节】已知A=(x-3)
(1)化简A;
(2)若x满足不等式组 且x为整数时,
求A的值.
题型
技巧9
条件法求值
解:
(1)A=
=
=
=
(2)
由①得:x<1,由②得:x>-1,
∴不等式组的解集为-1
12.【中考·齐齐哈尔】先化简,再求值:
其中x2+2x-15=0.
技巧10
整体法求值
解:
原式=
=
=
=
=
∵x2+2x-15=0,
∴x2+2x=15.
∴原式=
本题考查了分式的化简求值,解题关键是掌握分式的基本运算.先按照分式计算的顺序(先算乘除,再算加减)化简分式.再根据题目的需要,灵活运用条件x2+2x-15=0转化整体代入求值.
点拨:
同类变式
13.已知abc≠0且a+b+c=0,
求 的值.
技巧11
补项法求值
同类变式
14.阅读下面的解题过程:
已知: ,求 的值.
解:由 知x≠0,所以 =3,
即x+ =3.
技巧12
倒数法求值
所以 =32-2=7.
故 的值为 .
该题的解法叫做“倒数法”,请你利用“倒数法”解下面的题目:
已知 ,求 的值.
同类变式
15.已知4x-3y-6z=0,x+2y-7z=0,且xyz≠0,
求 的值.
技巧13
消元法求值
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
