【苏教版】高中数学必修一 第一章 集合
文档属性
| 名称 | 【苏教版】高中数学必修一 第一章 集合 |
|
|
| 格式 | zip | ||
| 文件大小 | 116.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-08-26 00:00:00 | ||
图片预览





文档简介
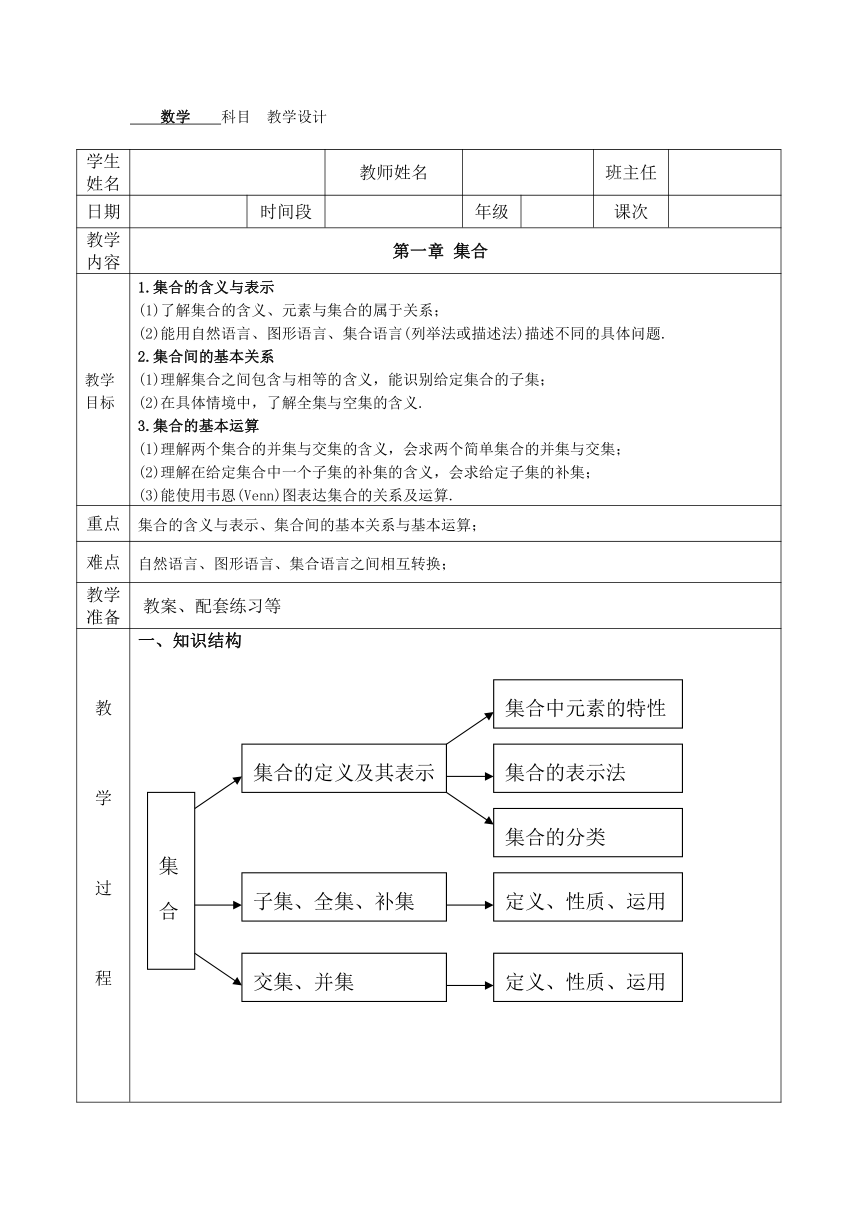
数学 科目 教学设计
学生姓名 教师姓名 班主任
日期 时间段 年级 课次
教学内容 第一章 集合
教学目标 1.集合的含义与表示(1)了解集合的含义、元素与集合的属于关系;(2)能用自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题.2.集合间的基本关系(1)理解集合之间包含与相等的含义,能识别给定集合的子集;(2)在具体情境中,了解全集与空集的含义.3.集合的基本运算(1)理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集;(2)理解在给定集合中一个子集的补集的含义,会求给定子集的补集;(3)能使用韦恩(Venn)图表达集合的关系及运算.
重点 集合的含义与表示、集合间的基本关系与基本运算;
难点 自然语言、图形语言、集合语言之间相互转换;
教学准备 教案、配套练习等
教学过程 一、知识结构第一课时 集合的含义【学习导航】 知识网络 学习要求1.初步理解集合的含义,常用数集及其记法; 2.集合中的元素的特性;3.理解属于关系和相等的意义;集合的分类; 4.集合的分类.【课堂互动】自学评价1.集合的含义: 构成一个集合(set). 一般用大写拉丁字母表示,如集合A,B等。2.集合中的元素:集合中的每一个对象称为该集合的元素(element),简称元。一般用小写拉丁字母表示.如a,b等.点睛:(1)集合是一个“整体”。 (2)构成集合的对象必须是“确定”的、“不同”的。其中“确定”是指构成集合的对象具有非常明确的特征,这个特征不是模棱两可的,对于任一对象而言,要么在这个集合中,要么不在这个集合中,二者必居其一;“不同”是指构成集合的各个对象是互不相同的。 (3)一个集合的对象具有广泛性,如数可以构成集合,点可以构成集合,商品也可以构成集合,即集合中的元素可以表示任何事物。3.集合中元素的特性:(1)确定性.设A 是一个给定的集合,x是某一元素,则x是A的元素,或者不是A的元素,两 种情况必有一种且只有一种成立.(2)互异性.对于一个给定的集合,它的任何两个元素都是不同的.(3)无序性.集合与其中元素的排列次序无关.4.常用数集及其记法: 一般地,自然数集记作_______ ,正整数集记作__________或___________整数集记作________,有理数记作_______,实数集记作________。5.元素与集合的关系:如果a是集合A的元素,就记作__________读作“________________”;如果a不是集合A的元素,就记作______或______读作“_______________”;6.集合的分类:按它的元素个数多少来分:(1) ________叫做有限集;(2)_________________叫做无限集;(3) __叫做空集,记为_______【典例精析】一、运用集合中元素的特性来解决问题【例1】下列研究的对象能否构成集合(1)世界上最高的山峰 (2)高一数学课本中的难题(3)中国国旗的颜色 (4)充分小的负数的全体(5)book中的字母 (6)立方等于本身的实数(7)不等式2x-8<13的正整数解【例2】集合M中的元素为1,x,x2-x,求x的范围?【例3】三个元素的集合1,a,,也可表示为0,a2,a+b,求a2005+ b2006的值. 二、运用元素与集合的关系来解决一些问题【例4】集合A中的元素由x=a+b(a∈Z,b∈Z)组成,判断下列元素与集合A的关系?(1)0 (2) (3)【例5】不包含-1,0,1的实数集A满足条件a∈A,则∈A,如果2∈A,求A中的元素?【选修延伸】【例6】设S是满足下列两个条件的实数所构成的集合: ①1S,②若,则,请解答下列问题:(1)若2∈S,则S中必有另外两个数,求出这两个数;(2)求证:若,则(3)在集合S中元素能否只有一个?请说明理由;【追踪训练】1.下列研究的对象能否构成集合① 某校个子较高的同学; ② 倒数等于本身的实数 ③ 所有的无理数④ 讲台上的一盒白粉笔 ⑤中国的直辖市 ⑥中国的大城市 2.下列写法正确的是___________________①Q ②当n∈N时,由所有(-1)n的数值组成的集合为无限集 ③R ④-1∈Z ⑤由book中的字母组成的集合与元素k,o,b组成的集合是同一个集合3.用∈或填空 1_______N -3_________N 0__________N ________N 1_______Z -3_________Q 0__________Z ________R 0_______N* ________R _______Q cos300_______Z4.由实数-x,|x|,,x,组成的集合最多含有元素的个数是_____个5. 已知集合A由+2,(a+1)2,+3+3三根元素组成,若1A,求实数的值。第二课时 集合的表示【学习导航】 知识网络学习要求1.集合的表示的常用方法:列举法、描述法; 2.初步理解集合相等的概念,并会初步运用,3.培养学生的逻辑思维能力和运算能力.【课堂互动】自学评价1. 集合的常用表示方法:(1)列举法将集合的元素一一列举出来,并____________ _____表示集合的方法叫列举法.注意:①元素与元素之间必须用“,”隔开; ②集合的元素必须是明确的; ③各元素的出现无顺序; ④集合里的元素不能重复; ⑤集合里的元素可以表示任何事物(2)描述法将集合的所有元素都具有的性质( )表示出来,写成_ ____的形式,称之为描述法.注意:①写清楚该集合中元素满足性质; ②不能出现未被说明的字母;③多层描述时,应当准确使用“或”,“且”; ④所有描述的内容都要写在集合的括号内;⑤用于描述的语句力求简明,准确.思考:还有其它表示集合的方法吗? 文字描述法:是一种特殊的描述法,如:{正整数},{三角形} 图示法(Venn图):用平面上封闭曲线的内部代集合.2. 集合相等如果两个集合A,B所含的元素完全相同,________ __ 则称这两个集合相等,记为: 【典例精析】一、用集合的两种常用方法具体地表示集合【例1】用列举法表示下列集合:(1)中国国旗的颜色的集合; (2)单词mathematics中的字母的集合;(3)自然数中不大于10的质数的集合; (4)同时满足的整数解的集合;(5)由所确定的实数集合.(6){(x,y)|3x+2y=16,x∈N,y∈N }【例2】用描述法表示下列集合:(1)所有被3整除的整数的集合;(2)使有意义的x的集合;(3)方程x2+x+1=0所有实数解的集合;(4)偶数的集合;(5)负奇数的集合;(6)不等式x-2>5的解集;(7)抛物线y=-x2+3x-6上所有点的集合;(8)图中阴影部分内点的集合; 【例3】已知A={a|},试用列举法表示集合A.二、有关集合相等方面的问题【例4】已知集合P={-1,a,b},Q={-1,a2,b2},且Q=P,求1+a2+b2的值.三、集合与方程的问题【例5】已知集合A=+=若集合A是空集,求实数a的取值范围。若集合是单元素集,求实数a的值,并把这个元素写出来。若集合A有两个元素,求实数a的取值范围。【选修延伸】【例6】 已知集合B={x|}有唯一元素,用列举法表示a的值构成的集合A.【追踪训练】1.用列举法表示下列集合:(1){x|x2+x-6=0}(2){x|x为15的正约数}(3){x|x为不大于10的正偶数}(4){(x,y)|0≤x≤2,0≤y<2,x,y∈Z}2. 用描述法表示下列集合:(1)奇数的集合;(2)正偶数的集合;(3)不等式2x-3>5的解集;(4)直角坐标平面内属于第四象限的点的集合; .3. 下列集合表示法正确的是 (1){1,2,2}; (2){Ф};(3){全体有理数}; (4)方程组的解的集合为{2,4};(5)不等式x2-5>0的解集为{x2-5>0}.4.集合A={x|y=x2+1},B={t|p=t2+1},C={y|x =},这三个集合的关系?5.已知A={x|},试用列举法表示集合A6. 已知A=+2=0,,若中至多有一个元素,求的取值范围。第三课时 子集、全集、补集【学习导航】知识网络学习要求1.了解集合之间包含关系的意义; 2.理解子集、真子集的概念和掌握它们的符号表示;3.子集、真子集的性质;4.了解全集的意义,理解补集的概念.【课堂互动】自学评价1.子集的概念及记法:如果集合A的任意一个元素都是集合B的元素( ),则称集合 A为集合B的子集(subset),记为_______或_______读作“__________”或“___________”可用右图表示: 注意:(1)A是B的子集的含义:任意x∈A,能推出x∈B;(2)不能理解为子集A是B中的“部分元素”所组成的集合.2.子集的性质:①AA ② ③,则(子集的传递性)3.真子集的概念及记法:如果,并且A≠B,这时集合 A称为集合B的真子集(proper set),记为_________或________读作“__________________”或“_________________”4.真子集的性质:①是任何非空集合的真子集符号表示为___________________② 真子集具备传递性符号表示为___________________5.全集的概念:如果集合U包含我们所要研究的各个集合,这时U可以看做一个全集(universal set)全集通常记作_____6.补集的概念:设____________,由U中不属于A的所有元素组成的集合称为U的子集A的补集(complementary set), 记为___________读作“____________”即:=_____________ 可用右图阴影部分来:__________________7.补集的性质:① =___________②=__________③=__________【典例精析】一、元素与集合之间、集合与集合之间的关系【例1】以下各组是什么关系,用适当的符号表示出来.a与{a} (2)0 与 (3)与{20,,} (4)S={-2,-1,1,2}, A={-1,1}, B={-2,2}; (5)S=R,A={x|x≤0,x∈R},B={x|x>0 ,x∈R };(6)S={x|x为地球人 },A={x|x 为中国人},B={x|x为外国人 }二、写出一个集合的子集、真子集及其个数公式【例2】①写出集合{a,b}的所有子集及其真子集;②写出集合{a,b,c}的所有子集及其真子集;【例3】已知集合,写出所有的集合A.【例4】已知M={1,2,3,4,5},非空集合P满足:①PM,②若,则6-∈P,写出所有的集合P?点睛:写子集,真子集要按一定顺序来写.①一个集合里有n个元素,那么它有2n个子集;②一个集合里有n个元素,那么它有2n-1个真子集;③一个集合里有n个元素,那么它有2n-2个非空真子集.三、运用子集的性质【例5】设集合A={x|x2+4x=0,x∈R},B={x|x2+2(a+1)x+a2-1=0,x∈R},若BA,求实数a的取值范围.四、补集的求法【例6】①方程组的解集为A,U=R,试求A及.②设全集U=R,A={x|x>1},B={x|x+a<0},是的真子集,求实数a的取值范围.【选修延伸】【例7】已知全集S={1,3x3+3x2+2x},集合A={1,|2x-1|},如果={0},则这样的实数x是否存在?若存在,求出x,若不存在,请说明理由.【追踪训练】1.判断下列表示是否正确:(1) a{a } {a }∈{a,b }(3) {a,b } {b,a } (4) {-1,1} {-1,0,1}(5) {-1,1}2.指出下列各组中集合A与B之间的关系.(1) A={-1,1}, B=Z; (2) A={1,3,5,15}, B={x|x是15的正约数};(3) A = N*, B=N(4) A ={x|x=1+a2,a∈N* } B={x|x=a2-4a+5,a∈N*}3.以下各组是什么关系,用适当的符号表来.(1) 与{0} (2) {-1,1}与{1,-1}(3) {(a,b)} 与{(b,a)} (4) 与{0,1,}4.若U=Z,A={x|x=2k,k∈Z},B={x|x=2k+1,k∈Z},则= = 5.已知{1,2 }M{1,2,3,4,5},则这样的集合M有多少个?6.已知M={1,2,3,4,5,6, 7,8,9},集合P满足:PM,且若,则10- ∈P,则这样的集合P有多少个? 7.设全集是数集U={2,3,a2+2a-3},已知A={b,2},={5},求实数a,b的值.8.已知集合A={x|x2-1=0 },B={x|x2-2ax+b=0} ,BA,求a,b满足的条件。9.已知集合A={x|x=a+,a∈Z},B={x|x=,b∈Z},C={x|x=,c∈Z},试判断A、B、C满足的关系第四课时 集合的运算---交集【学习导航】 知识网络学习要求1.理解交集的概念及其交集的性质;2.会求已知两个集合的交集; 3.理解区间的表示法;4.提高学生的逻辑思维能力.【课堂互动】自学评价1.交集的定义:一般地,_______________________________,称为A与B交集 (intersection set),记作____________读作“___________”.交集的定义用符号语言表示为:_______________________交集的定义用图形语言表示为:_______________________注意:(1)交集(A∩B)实质上是A与B的公共元素所组成的集合. (2)当集合A与B没有公共元素时,不能说A与B没有交集,而是A∩B=.2.交集的常用性质: (1) A∩A = A; (2) A∩=; (3) A∩B = B∩A; (4)(A∩B)∩C =A∩(B∩C); (5) A∩B A, A∩BB3.集合的交集与子集:思考: A∩B=A,可能成立吗?【答】________________4.区间的表示法:设a,b是两个实数,且a0},B={x|x≤1},求A∩B;(3)设A={x|x=3k,k∈Z},B={y|y=3k+1 k∈Z },C={z|z=3k+2,k∈Z},D={x|x=6k+1,k∈Z}, 求A∩B; A∩C;C∩B;D∩B;【例2】已知数集 A={a2,a+1,-3},数集B={a-3,a-2,a2+1},若A∩B={-3},求a的值.【例3】(1)设集合A={y|y=x2-2x+3,x∈R},B={y|y=-x2+2x+10,x∈R},求A∩B (2)设集合A={(x,y)|y=x+1,x∈R}, B={(x,y)|y=-x2+2x+,x∈R},求A∩B;二、运用交集的性质解题【例4】已知集合A={2,5},B={x|x2+px+q=0,x∈R}(1)若B={5},求p,q的值.(2)若A∩B= B ,求实数p,q满足的条件.三、借助Venn图解决集合的运算问题【例5】已知全集U={不大于20的质数},M,N是U的两个子集,且满足M∩()={3,5}, {7,19},{2,17},求M,N的值.【选修延伸】【例6】已知集合A={x|x2-4mx+2m+6=0},B={x|x<0},若A∩B ≠,求实数m的取值范围.【追踪训练】1. 设集合A={小于7的正偶数},B={-2,0,2,4},求A∩B;2. 设集合A={x|x≥0},B={x|x≤0,x∈R},求A∩B;3. 设集合A={(x,y)|y=-4x+1,x∈R},B={(x,y)|x=y2-1}求A∩B; 4. 设集合A={x||x=2k+1,k∈Z},B={y|y=2k-1,k∈Z},C={x|x=2k ,k∈Z},求A∩B,B∩C. 5.已知集合A={x|x2+x-6=0},B={x|mx+1=0=0},若A∩B =B,求实数m所构成的集合M.6.已知集合M={x|x≤-1},N={x|x>a-2},若M∩N≠,则a满足的条件是什么?第五课时 集合的运算---并集【学习导航】 知识网络 学习要求1.理解并集的概念及其并集的性质; 2.会求已知两个集合的并集; 3.初步会求集合的运算的综合问题; 4.提高学生的分析解决问题的能力.【课堂互动】自学评价1.并集的定义:一般地,____________ ___,称为集合A与集合B的并集(unionset) 记作__________读作“___________”.交集的定义用符号语言表示为: __________________________________交集的定义用图形语言表示为:_________________________________注意:并集(A∪B)实质上是A与B的所有元素所组成的集合,但是公共元素在同一个集合中要注意元素的互异性.2.并集的常用性质:(1) A∪A = A; (2) A∪= A; (3)A∪B = B∪A; (4)(A∪B)∪C =A∪(B∪C); (5) AA∪B, BA∪B3.集合的并集与子集:思考: A∪B=A,可能成立吗?A∪是什么集合?【答】_____________结论:A∪B=BAB【典例精析】一、求集合的交、并、补集【例1】根据下面给出的A 、B,求A∪B ①A={-1,0,1},B={0,1,2,3};②A={y|y=x2-2x},B={x||x|≤3};③A={梯形},B={平行四边形}.【例2】已知全集U=R,A={x|-4≤x<2},B=(-1,3),P={x|x≤0,或x≥},求:①(A∪B)∩P ②∪P ③ (A∩B)∪ .【例3】已知集合A={y|y=x-1,x∈R},B={(x,y)|y=x2-1,x∈R},C={x|y=x+1,y≥3},求:(A∪C)∩B.二、运用并集的性质解题【例4】已知集合A={x|x2-1=0 },B={x|x2-2ax+b=0},A∪B=A,求a,b的值或a,b所满足的条件.【选修延伸】【例5】若A={x|x2-ax+a2-19=0},B={x|x2-5x+6=0},C={x|x2+2x-8=0},(1)若A∪B=A∩B,求a的值;(2) A∩B,A∩C=,求a的值.【追踪训练】1.设A=(-1,3],B=[2,4),求A∪B;2.已知A={y|y=x2-1},B={y|x2=-y+2},求A∪B;3.写出阴影部分所表示的集合: 4.集合U={1,2,3,4,5,6},B={1,4} A={2,3,5} .求:()∩ 5.若集合P={1,2,4,m},Q={2,m2},满足P∪Q={1,2,4,m},求实数m的值组成的集合.6.已知集合A={x|x2-4x+3=0},B={x|x2-ax-1=0},C={x|x2-mx+1=0},且A∪B=A,A∩C=C,求a,m的值或取范围.第六课时 交集、并集综合应用【学习导航】学习要求:1.熟练掌握交集、并集的概念及其性质。2.注意用数轴、文氏图来解决交集、并集问题。3.分类讨论思想在解题中的应用。【精典范例】一、交集并集性质的应用【例1】已知集合A={(x,y)|x2-y2-y=4},B={(x,y)|x2-xy-2y2=0},C={(x,y)|x-2y=0},D{(x,y)|x+y=0}。(1)判断B、C、D间的关系;(2)求A∩B。二、交集、并集在实际生活中的应用【例2】某学校高一(5)班有学生50人,参加航模小组的有25人,参加电脑小组的有32人,求既参加航模小组,又参加电脑小组的人数的最大值和最小值。三、数形结合思想与交集并集的应用【例3】已知集合A={x|-20},B={x|a≤x≤b},满足A∩B={x|0-2},求a、b的值。四、分类讨论思想与交集并集的综合应用【例4】已知集合A={x|x2-4x+3=0},B={x|x2-ax+a-1=0},C={x|x2-mx+1=0},且A∪B=A,A∩C=C,求a,m的值或取值范围。【追踪训练】集合A={x|x<-3,或x>3},B={x|x<1,或x>4},则A∩B=__________.集合A={a2,a+1,-3},B={a-3,2a-1,a2+1},若A∩B={-3},则a的值为___________.3.集合{3,x,x2-2x}中,x应满足的条件是___________.4.已知A={x|x2-px+15=0},B={x|x2-ax-b=0},且A∪B={2,3,5},A∩B={3},求p,a,b的值。5.设A={x|x2+4x=0},B={x|x2+2(a+1)x+a2-1=0,a∈R}.(1)若A∩B=B,求实数a的值。(2)若A∪B=B,求实数a的值。第七课时 小结与复习课【学习导航】 知识网络 学习要求1.掌握集合的有关基本义概念,运用集合的概念解决问题;2.掌握集合的包含关系(子集、真子集);3.掌握集合的运算(交、并、补);4.再解决有关集合问题时,要注意各种思想方法(数形集结合、补集思想、分类讨论)的运用.【课堂互动】自学评价1.对于集合的问题:要确定属于哪一类集合(数集,点集,或某类图形集),然后再确定处理此类问题的方法.2.关于集合中的运算,一般应把各参与运算的集合化到最简形式,然后再进行运算.3.含参数的集合问题,多根据集合的的互异性处理,有时需要用到分类讨论、数形集结合的思想.4.集合问题多与函数、方程有关,要注意各类知识的融会贯通.【典例精析】【例1】设U={1,2,3,4,5},且A∩B={2},()∩B ={4}, ()∩={1,5},则下列结论正确的是 ①3∈A,3∈B ②2∈,3∈B 3∈,3∈A ④3∈,3∈【例2】全集U=R,集合A={x|x2-x-6<0},B={x|x2+2x-8>0},C={x|x2-4ax+3a2<0}, (1)试求a的取值范围,使A∩BC; (2)试求a的取值范围,使【例3】 已知集合A={x|x2+4ax-4a+3=0}, B={x|x2+(a-1)x+a2=0},C={x|x2+2ax-2a=0}, 其中至少有一个集合不是空集,求实数a的取值范围.【追踪训练】1.设U={x|0教 学反 思
集合
定义、性质、运用
交集、并集
集合的定义及其表示
子集、全集、补集
集合中元素的特性
集合的分类
集合的表示法
定义、性质、运用
集合
集合定义
确定性
元素的特性
集合的分类
无序性
互异性
有限集
无限集
空集
集合的表示
描述法
列举法
集
合
的
关
系
包含
全集
相等
子集
真子集
补集
交集
定义
集合的运算
运用
性质
并集
定义
集合的运算
运用
性质
集合
集合与集合的关系
集合的概念
集合的表示法
列举法
描述法
包含关系
元素的性质
分类
集合运算
确定性
无序性
互异性
有限集
无限集
空集
子集
相 等
真子集
并集
交集
补集
学生姓名 教师姓名 班主任
日期 时间段 年级 课次
教学内容 第一章 集合
教学目标 1.集合的含义与表示(1)了解集合的含义、元素与集合的属于关系;(2)能用自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题.2.集合间的基本关系(1)理解集合之间包含与相等的含义,能识别给定集合的子集;(2)在具体情境中,了解全集与空集的含义.3.集合的基本运算(1)理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集;(2)理解在给定集合中一个子集的补集的含义,会求给定子集的补集;(3)能使用韦恩(Venn)图表达集合的关系及运算.
重点 集合的含义与表示、集合间的基本关系与基本运算;
难点 自然语言、图形语言、集合语言之间相互转换;
教学准备 教案、配套练习等
教学过程 一、知识结构第一课时 集合的含义【学习导航】 知识网络 学习要求1.初步理解集合的含义,常用数集及其记法; 2.集合中的元素的特性;3.理解属于关系和相等的意义;集合的分类; 4.集合的分类.【课堂互动】自学评价1.集合的含义: 构成一个集合(set). 一般用大写拉丁字母表示,如集合A,B等。2.集合中的元素:集合中的每一个对象称为该集合的元素(element),简称元。一般用小写拉丁字母表示.如a,b等.点睛:(1)集合是一个“整体”。 (2)构成集合的对象必须是“确定”的、“不同”的。其中“确定”是指构成集合的对象具有非常明确的特征,这个特征不是模棱两可的,对于任一对象而言,要么在这个集合中,要么不在这个集合中,二者必居其一;“不同”是指构成集合的各个对象是互不相同的。 (3)一个集合的对象具有广泛性,如数可以构成集合,点可以构成集合,商品也可以构成集合,即集合中的元素可以表示任何事物。3.集合中元素的特性:(1)确定性.设A 是一个给定的集合,x是某一元素,则x是A的元素,或者不是A的元素,两 种情况必有一种且只有一种成立.(2)互异性.对于一个给定的集合,它的任何两个元素都是不同的.(3)无序性.集合与其中元素的排列次序无关.4.常用数集及其记法: 一般地,自然数集记作_______ ,正整数集记作__________或___________整数集记作________,有理数记作_______,实数集记作________。5.元素与集合的关系:如果a是集合A的元素,就记作__________读作“________________”;如果a不是集合A的元素,就记作______或______读作“_______________”;6.集合的分类:按它的元素个数多少来分:(1) ________叫做有限集;(2)_________________叫做无限集;(3) __叫做空集,记为_______【典例精析】一、运用集合中元素的特性来解决问题【例1】下列研究的对象能否构成集合(1)世界上最高的山峰 (2)高一数学课本中的难题(3)中国国旗的颜色 (4)充分小的负数的全体(5)book中的字母 (6)立方等于本身的实数(7)不等式2x-8<13的正整数解【例2】集合M中的元素为1,x,x2-x,求x的范围?【例3】三个元素的集合1,a,,也可表示为0,a2,a+b,求a2005+ b2006的值. 二、运用元素与集合的关系来解决一些问题【例4】集合A中的元素由x=a+b(a∈Z,b∈Z)组成,判断下列元素与集合A的关系?(1)0 (2) (3)【例5】不包含-1,0,1的实数集A满足条件a∈A,则∈A,如果2∈A,求A中的元素?【选修延伸】【例6】设S是满足下列两个条件的实数所构成的集合: ①1S,②若,则,请解答下列问题:(1)若2∈S,则S中必有另外两个数,求出这两个数;(2)求证:若,则(3)在集合S中元素能否只有一个?请说明理由;【追踪训练】1.下列研究的对象能否构成集合① 某校个子较高的同学; ② 倒数等于本身的实数 ③ 所有的无理数④ 讲台上的一盒白粉笔 ⑤中国的直辖市 ⑥中国的大城市 2.下列写法正确的是___________________①Q ②当n∈N时,由所有(-1)n的数值组成的集合为无限集 ③R ④-1∈Z ⑤由book中的字母组成的集合与元素k,o,b组成的集合是同一个集合3.用∈或填空 1_______N -3_________N 0__________N ________N 1_______Z -3_________Q 0__________Z ________R 0_______N* ________R _______Q cos300_______Z4.由实数-x,|x|,,x,组成的集合最多含有元素的个数是_____个5. 已知集合A由+2,(a+1)2,+3+3三根元素组成,若1A,求实数的值。第二课时 集合的表示【学习导航】 知识网络学习要求1.集合的表示的常用方法:列举法、描述法; 2.初步理解集合相等的概念,并会初步运用,3.培养学生的逻辑思维能力和运算能力.【课堂互动】自学评价1. 集合的常用表示方法:(1)列举法将集合的元素一一列举出来,并____________ _____表示集合的方法叫列举法.注意:①元素与元素之间必须用“,”隔开; ②集合的元素必须是明确的; ③各元素的出现无顺序; ④集合里的元素不能重复; ⑤集合里的元素可以表示任何事物(2)描述法将集合的所有元素都具有的性质( )表示出来,写成_ ____的形式,称之为描述法.注意:①写清楚该集合中元素满足性质; ②不能出现未被说明的字母;③多层描述时,应当准确使用“或”,“且”; ④所有描述的内容都要写在集合的括号内;⑤用于描述的语句力求简明,准确.思考:还有其它表示集合的方法吗? 文字描述法:是一种特殊的描述法,如:{正整数},{三角形} 图示法(Venn图):用平面上封闭曲线的内部代集合.2. 集合相等如果两个集合A,B所含的元素完全相同,________ __ 则称这两个集合相等,记为: 【典例精析】一、用集合的两种常用方法具体地表示集合【例1】用列举法表示下列集合:(1)中国国旗的颜色的集合; (2)单词mathematics中的字母的集合;(3)自然数中不大于10的质数的集合; (4)同时满足的整数解的集合;(5)由所确定的实数集合.(6){(x,y)|3x+2y=16,x∈N,y∈N }【例2】用描述法表示下列集合:(1)所有被3整除的整数的集合;(2)使有意义的x的集合;(3)方程x2+x+1=0所有实数解的集合;(4)偶数的集合;(5)负奇数的集合;(6)不等式x-2>5的解集;(7)抛物线y=-x2+3x-6上所有点的集合;(8)图中阴影部分内点的集合; 【例3】已知A={a|},试用列举法表示集合A.二、有关集合相等方面的问题【例4】已知集合P={-1,a,b},Q={-1,a2,b2},且Q=P,求1+a2+b2的值.三、集合与方程的问题【例5】已知集合A=+=若集合A是空集,求实数a的取值范围。若集合是单元素集,求实数a的值,并把这个元素写出来。若集合A有两个元素,求实数a的取值范围。【选修延伸】【例6】 已知集合B={x|}有唯一元素,用列举法表示a的值构成的集合A.【追踪训练】1.用列举法表示下列集合:(1){x|x2+x-6=0}(2){x|x为15的正约数}(3){x|x为不大于10的正偶数}(4){(x,y)|0≤x≤2,0≤y<2,x,y∈Z}2. 用描述法表示下列集合:(1)奇数的集合;(2)正偶数的集合;(3)不等式2x-3>5的解集;(4)直角坐标平面内属于第四象限的点的集合; .3. 下列集合表示法正确的是 (1){1,2,2}; (2){Ф};(3){全体有理数}; (4)方程组的解的集合为{2,4};(5)不等式x2-5>0的解集为{x2-5>0}.4.集合A={x|y=x2+1},B={t|p=t2+1},C={y|x =},这三个集合的关系?5.已知A={x|},试用列举法表示集合A6. 已知A=+2=0,,若中至多有一个元素,求的取值范围。第三课时 子集、全集、补集【学习导航】知识网络学习要求1.了解集合之间包含关系的意义; 2.理解子集、真子集的概念和掌握它们的符号表示;3.子集、真子集的性质;4.了解全集的意义,理解补集的概念.【课堂互动】自学评价1.子集的概念及记法:如果集合A的任意一个元素都是集合B的元素( ),则称集合 A为集合B的子集(subset),记为_______或_______读作“__________”或“___________”可用右图表示: 注意:(1)A是B的子集的含义:任意x∈A,能推出x∈B;(2)不能理解为子集A是B中的“部分元素”所组成的集合.2.子集的性质:①AA ② ③,则(子集的传递性)3.真子集的概念及记法:如果,并且A≠B,这时集合 A称为集合B的真子集(proper set),记为_________或________读作“__________________”或“_________________”4.真子集的性质:①是任何非空集合的真子集符号表示为___________________② 真子集具备传递性符号表示为___________________5.全集的概念:如果集合U包含我们所要研究的各个集合,这时U可以看做一个全集(universal set)全集通常记作_____6.补集的概念:设____________,由U中不属于A的所有元素组成的集合称为U的子集A的补集(complementary set), 记为___________读作“____________”即:=_____________ 可用右图阴影部分来:__________________7.补集的性质:① =___________②=__________③=__________【典例精析】一、元素与集合之间、集合与集合之间的关系【例1】以下各组是什么关系,用适当的符号表示出来.a与{a} (2)0 与 (3)与{20,,} (4)S={-2,-1,1,2}, A={-1,1}, B={-2,2}; (5)S=R,A={x|x≤0,x∈R},B={x|x>0 ,x∈R };(6)S={x|x为地球人 },A={x|x 为中国人},B={x|x为外国人 }二、写出一个集合的子集、真子集及其个数公式【例2】①写出集合{a,b}的所有子集及其真子集;②写出集合{a,b,c}的所有子集及其真子集;【例3】已知集合,写出所有的集合A.【例4】已知M={1,2,3,4,5},非空集合P满足:①PM,②若,则6-∈P,写出所有的集合P?点睛:写子集,真子集要按一定顺序来写.①一个集合里有n个元素,那么它有2n个子集;②一个集合里有n个元素,那么它有2n-1个真子集;③一个集合里有n个元素,那么它有2n-2个非空真子集.三、运用子集的性质【例5】设集合A={x|x2+4x=0,x∈R},B={x|x2+2(a+1)x+a2-1=0,x∈R},若BA,求实数a的取值范围.四、补集的求法【例6】①方程组的解集为A,U=R,试求A及.②设全集U=R,A={x|x>1},B={x|x+a<0},是的真子集,求实数a的取值范围.【选修延伸】【例7】已知全集S={1,3x3+3x2+2x},集合A={1,|2x-1|},如果={0},则这样的实数x是否存在?若存在,求出x,若不存在,请说明理由.【追踪训练】1.判断下列表示是否正确:(1) a{a } {a }∈{a,b }(3) {a,b } {b,a } (4) {-1,1} {-1,0,1}(5) {-1,1}2.指出下列各组中集合A与B之间的关系.(1) A={-1,1}, B=Z; (2) A={1,3,5,15}, B={x|x是15的正约数};(3) A = N*, B=N(4) A ={x|x=1+a2,a∈N* } B={x|x=a2-4a+5,a∈N*}3.以下各组是什么关系,用适当的符号表来.(1) 与{0} (2) {-1,1}与{1,-1}(3) {(a,b)} 与{(b,a)} (4) 与{0,1,}4.若U=Z,A={x|x=2k,k∈Z},B={x|x=2k+1,k∈Z},则= = 5.已知{1,2 }M{1,2,3,4,5},则这样的集合M有多少个?6.已知M={1,2,3,4,5,6, 7,8,9},集合P满足:PM,且若,则10- ∈P,则这样的集合P有多少个? 7.设全集是数集U={2,3,a2+2a-3},已知A={b,2},={5},求实数a,b的值.8.已知集合A={x|x2-1=0 },B={x|x2-2ax+b=0} ,BA,求a,b满足的条件。9.已知集合A={x|x=a+,a∈Z},B={x|x=,b∈Z},C={x|x=,c∈Z},试判断A、B、C满足的关系第四课时 集合的运算---交集【学习导航】 知识网络学习要求1.理解交集的概念及其交集的性质;2.会求已知两个集合的交集; 3.理解区间的表示法;4.提高学生的逻辑思维能力.【课堂互动】自学评价1.交集的定义:一般地,_______________________________,称为A与B交集 (intersection set),记作____________读作“___________”.交集的定义用符号语言表示为:_______________________交集的定义用图形语言表示为:_______________________注意:(1)交集(A∩B)实质上是A与B的公共元素所组成的集合. (2)当集合A与B没有公共元素时,不能说A与B没有交集,而是A∩B=.2.交集的常用性质: (1) A∩A = A; (2) A∩=; (3) A∩B = B∩A; (4)(A∩B)∩C =A∩(B∩C); (5) A∩B A, A∩BB3.集合的交集与子集:思考: A∩B=A,可能成立吗?【答】________________4.区间的表示法:设a,b是两个实数,且a
集合
定义、性质、运用
交集、并集
集合的定义及其表示
子集、全集、补集
集合中元素的特性
集合的分类
集合的表示法
定义、性质、运用
集合
集合定义
确定性
元素的特性
集合的分类
无序性
互异性
有限集
无限集
空集
集合的表示
描述法
列举法
集
合
的
关
系
包含
全集
相等
子集
真子集
补集
交集
定义
集合的运算
运用
性质
并集
定义
集合的运算
运用
性质
集合
集合与集合的关系
集合的概念
集合的表示法
列举法
描述法
包含关系
元素的性质
分类
集合运算
确定性
无序性
互异性
有限集
无限集
空集
子集
相 等
真子集
并集
交集
补集
