人教版七年级上册2整式的加减复习课件 (共19张PPT)
文档属性
| 名称 | 人教版七年级上册2整式的加减复习课件 (共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 285.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-28 08:58:47 | ||
图片预览





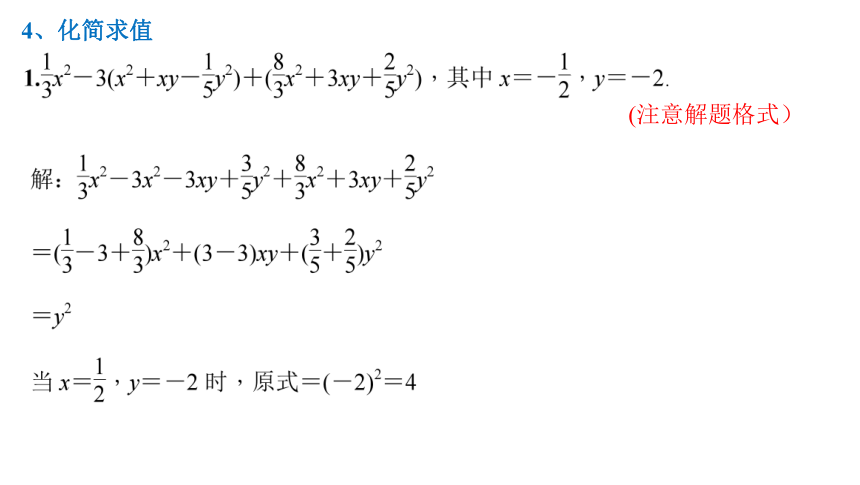
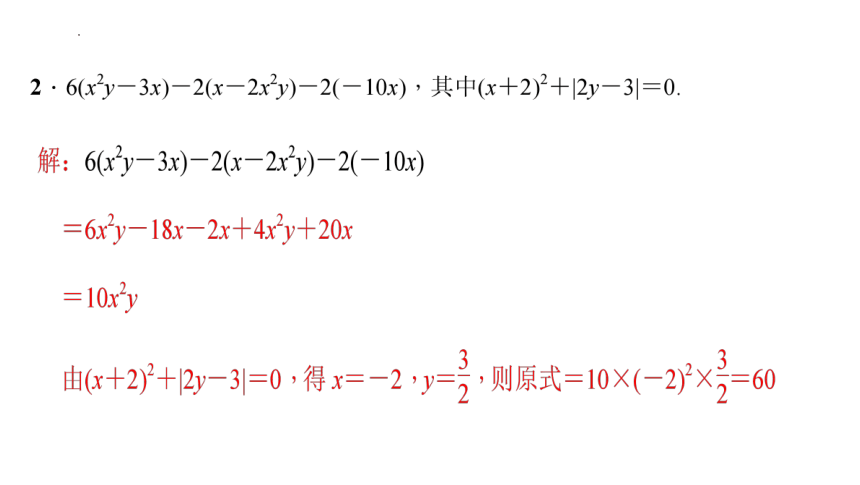
文档简介
(共19张PPT)
第二章 整式的加减复习
整 式 的 加 减
用字母表示数
单项式:
多项式:
去括号:
同类项:
合并同类项:
整式的加减:
系数(数字因数,记得带上符号)、次数(所有字母的指数相加)
项(每一个单项式)、次数(最高次项的次数)、常数项
定义、“两相同(字母+指数) 、两无关(系数+顺序)”
定义、法则(系数相加,字母和指数不变)、步骤
法则(括号内、各项)
步 骤(去括号,再合并同类项)
整 式
本章知识结构图
(次数为0)
把多项式中的_________合并成一项,叫做合并同类项,合并同类项后,所得项的系数是合并前各同类项的系数的____,且字母连同它的指数_______.
(1)计算2a2+a2,结果正确的是( )
A.2a4 B.2a2 C.3a4 D.3a2
同类项
和
不变
D
1.同类项、合并同类项
(2)如果单项式 -2xm+3与2x4yn+3 的和是单项式,那么(m+n)2019的值为( )(解题关键:单项式对应字母的指数相同)
-1
差
如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号_______;如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号________.
相同
相反
2.去括号
练习:去掉下列各式中的括号:
(1) (x+y)-z=_______________; (2) x-(y+z)=______________;
(3) -1-2(x-y)=_______________; (4) 2(a-b)-3(x+y)=____________.
x+y-z
x-y-z
-1-2x+2y
2a-2b-3x-3y
-x+y-z的相反数是( )
A.-x-y+z B.x-y+z
C.x+y-z D.x+y+z
B
3.求相反数
解题关键:求某个数的相反数,在整体前添上负号,然后去括号化简
-x+y-z的相反数是- ( - x+y-z)= x-y+z
x-y的相反数= - (x-y)
= - x+y
= y- x
(x-y)的相反数的三种写法熟练转化
4、化简求值
(注意解题格式)
(1)已知a2-a-4=0,求4a2-2(a2-a+3)-(a2-a-4)-4a的值.
解: 4a2-2(a2-a+3)-(a2-a-4)-4a
=4a2-2a2+2a-6-a2+a+4-4a
=a2-a-2.
又因为a2-a-4=0,所以a2-a=4,所以原式=4-2=2
5、求某个未知整体的值
已知某一个整体的值,求另外一个多项式的值,将多项式化简后观察其与已知整体的值的关系,通常有:相等、相反、倍数的关系。
解析: a2-b2 =a2-ab+ab-b2=15
a2-2ab+b2 = a2-ab - (ab-b2)=3
已知某两个整体的值,求另外一个多项式的值,通常是将两个已知整体进行加、减、乘运算
(2)若a2-ab=9,且ab-b2=6,
则a2-b2=____,a2-2ab+b2=____.
6、某个多项式的值与未知数x或y无关
解题技巧:与谁无关,谁的系数为0
(2).若x2+ax-2y+7-(bx2-2x+9y-1)的值与x无关,求-a-b的值.
解: x2+ax-2y+7-(bx2-2x+9y-1)
=x2+ax-2y+7-bx2+2x-9y+1
=(1-b)x2+(a+2)x-11y+8.
因为该整式的值与x无关,所以1-b=0,a+2=0,得b=1,a=-2.
所以-a-b=-(-2)-1=1
如果用a、b分别表示一个两位数字的十位数字和个位数字,那么这个两位数字可以表示为 ;交换这个两位数的十位数字和个位数字,得到的新两位数是 ;这两个两位数的和是 ,他能被 整除。如果把这两个两位数相减,你得到的规律是 。
10a+b
10b+a
10a+b+(10b+a)=11a+11b
11
9a-9b能被9整除
(课本P76 拓广探索)
7、用字母来表示两位数、三位数等
a
b
有三个连续偶数,若中间一个偶数为2n,则另两个偶数
为________________,这三个连续偶数的和为____.
2n-2,2n+2
6n
三个连续奇数,最小的一个是2n+1(n为自然数),则这三个连续奇数
的和为( )
A.6n+6 B. 2n+9 C. 6n+9 D.6n+3
C
①
②
8、用字母来表示奇数、偶数
若将x-y看成一个整体,则化简(x-y)2-3(x-y)-4(x-y)2+5(x-y)的
结果是( )
A. 2(x-y)2-3(x-y) B. 2(x-y)-3(x-y)2
C. (x-y)-3(x-y)2 D. 2(x-y)2-(x-y)
B
9、将某个多项式看成整体进行化简
课本P73 拓广探索第12题
10、列整式解决实际问题
(课本67页例5)
(1)两船从同一港口出发反向而行,甲船顺水,乙船逆水,两船
在静水中速度都是50千米/时,水流速度是a千米/时.
问:(1)2小时后两船相距多远?
(2)2小时后甲船比乙船多航行多少千米?
思考 超过部分如何表示
(1)若P是三次多项式,Q也是三次多项式,P+Q一定是( )
A.三次多项式 B.六次多项式 C.不高于三次的多项式或单项式 D单项式
C
(2)已知M=4x2-3x-2,N=6x2-3x+6,则M,N的大小关系是( )
M>N B. M=N C.M<N D.以上结论都不对
C
11、有关多项式的题型
(解题技巧:将x代入具体数值,例:x=0)
C
(3)黑板上有一道题,是一个多项式减去3x2-5x+1,某同学由于大意,将减号抄成了加号,得出的结果是5x2+3x-7,求出这道题的正确结果.
同类型题:《新课程》45页 能力提升 第九题
原题: - (3x2-5x+1)=
大意抄错: +(3x2-5x+1)= 5x2+3x-7
解:该多项式为(5x2+3x-7)-(3x2-5x+1)=2x2+8x-8.所以正确的结果为(2x2+8x-8)-(3x2-5x+1)=-x2+13x-9
分析:
第二章 整式的加减复习
整 式 的 加 减
用字母表示数
单项式:
多项式:
去括号:
同类项:
合并同类项:
整式的加减:
系数(数字因数,记得带上符号)、次数(所有字母的指数相加)
项(每一个单项式)、次数(最高次项的次数)、常数项
定义、“两相同(字母+指数) 、两无关(系数+顺序)”
定义、法则(系数相加,字母和指数不变)、步骤
法则(括号内、各项)
步 骤(去括号,再合并同类项)
整 式
本章知识结构图
(次数为0)
把多项式中的_________合并成一项,叫做合并同类项,合并同类项后,所得项的系数是合并前各同类项的系数的____,且字母连同它的指数_______.
(1)计算2a2+a2,结果正确的是( )
A.2a4 B.2a2 C.3a4 D.3a2
同类项
和
不变
D
1.同类项、合并同类项
(2)如果单项式 -2xm+3与2x4yn+3 的和是单项式,那么(m+n)2019的值为( )(解题关键:单项式对应字母的指数相同)
-1
差
如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号_______;如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号________.
相同
相反
2.去括号
练习:去掉下列各式中的括号:
(1) (x+y)-z=_______________; (2) x-(y+z)=______________;
(3) -1-2(x-y)=_______________; (4) 2(a-b)-3(x+y)=____________.
x+y-z
x-y-z
-1-2x+2y
2a-2b-3x-3y
-x+y-z的相反数是( )
A.-x-y+z B.x-y+z
C.x+y-z D.x+y+z
B
3.求相反数
解题关键:求某个数的相反数,在整体前添上负号,然后去括号化简
-x+y-z的相反数是- ( - x+y-z)= x-y+z
x-y的相反数= - (x-y)
= - x+y
= y- x
(x-y)的相反数的三种写法熟练转化
4、化简求值
(注意解题格式)
(1)已知a2-a-4=0,求4a2-2(a2-a+3)-(a2-a-4)-4a的值.
解: 4a2-2(a2-a+3)-(a2-a-4)-4a
=4a2-2a2+2a-6-a2+a+4-4a
=a2-a-2.
又因为a2-a-4=0,所以a2-a=4,所以原式=4-2=2
5、求某个未知整体的值
已知某一个整体的值,求另外一个多项式的值,将多项式化简后观察其与已知整体的值的关系,通常有:相等、相反、倍数的关系。
解析: a2-b2 =a2-ab+ab-b2=15
a2-2ab+b2 = a2-ab - (ab-b2)=3
已知某两个整体的值,求另外一个多项式的值,通常是将两个已知整体进行加、减、乘运算
(2)若a2-ab=9,且ab-b2=6,
则a2-b2=____,a2-2ab+b2=____.
6、某个多项式的值与未知数x或y无关
解题技巧:与谁无关,谁的系数为0
(2).若x2+ax-2y+7-(bx2-2x+9y-1)的值与x无关,求-a-b的值.
解: x2+ax-2y+7-(bx2-2x+9y-1)
=x2+ax-2y+7-bx2+2x-9y+1
=(1-b)x2+(a+2)x-11y+8.
因为该整式的值与x无关,所以1-b=0,a+2=0,得b=1,a=-2.
所以-a-b=-(-2)-1=1
如果用a、b分别表示一个两位数字的十位数字和个位数字,那么这个两位数字可以表示为 ;交换这个两位数的十位数字和个位数字,得到的新两位数是 ;这两个两位数的和是 ,他能被 整除。如果把这两个两位数相减,你得到的规律是 。
10a+b
10b+a
10a+b+(10b+a)=11a+11b
11
9a-9b能被9整除
(课本P76 拓广探索)
7、用字母来表示两位数、三位数等
a
b
有三个连续偶数,若中间一个偶数为2n,则另两个偶数
为________________,这三个连续偶数的和为____.
2n-2,2n+2
6n
三个连续奇数,最小的一个是2n+1(n为自然数),则这三个连续奇数
的和为( )
A.6n+6 B. 2n+9 C. 6n+9 D.6n+3
C
①
②
8、用字母来表示奇数、偶数
若将x-y看成一个整体,则化简(x-y)2-3(x-y)-4(x-y)2+5(x-y)的
结果是( )
A. 2(x-y)2-3(x-y) B. 2(x-y)-3(x-y)2
C. (x-y)-3(x-y)2 D. 2(x-y)2-(x-y)
B
9、将某个多项式看成整体进行化简
课本P73 拓广探索第12题
10、列整式解决实际问题
(课本67页例5)
(1)两船从同一港口出发反向而行,甲船顺水,乙船逆水,两船
在静水中速度都是50千米/时,水流速度是a千米/时.
问:(1)2小时后两船相距多远?
(2)2小时后甲船比乙船多航行多少千米?
思考 超过部分如何表示
(1)若P是三次多项式,Q也是三次多项式,P+Q一定是( )
A.三次多项式 B.六次多项式 C.不高于三次的多项式或单项式 D单项式
C
(2)已知M=4x2-3x-2,N=6x2-3x+6,则M,N的大小关系是( )
M>N B. M=N C.M<N D.以上结论都不对
C
11、有关多项式的题型
(解题技巧:将x代入具体数值,例:x=0)
C
(3)黑板上有一道题,是一个多项式减去3x2-5x+1,某同学由于大意,将减号抄成了加号,得出的结果是5x2+3x-7,求出这道题的正确结果.
同类型题:《新课程》45页 能力提升 第九题
原题: - (3x2-5x+1)=
大意抄错: +(3x2-5x+1)= 5x2+3x-7
解:该多项式为(5x2+3x-7)-(3x2-5x+1)=2x2+8x-8.所以正确的结果为(2x2+8x-8)-(3x2-5x+1)=-x2+13x-9
分析:
