鲁教版(五四制)八年级下册9.9利用位似放缩图形 课件(共19张PPT)
文档属性
| 名称 | 鲁教版(五四制)八年级下册9.9利用位似放缩图形 课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 83.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-28 09:10:02 | ||
图片预览





文档简介
(共19张PPT)
第九章第九节利用位似放缩图形
知识回顾
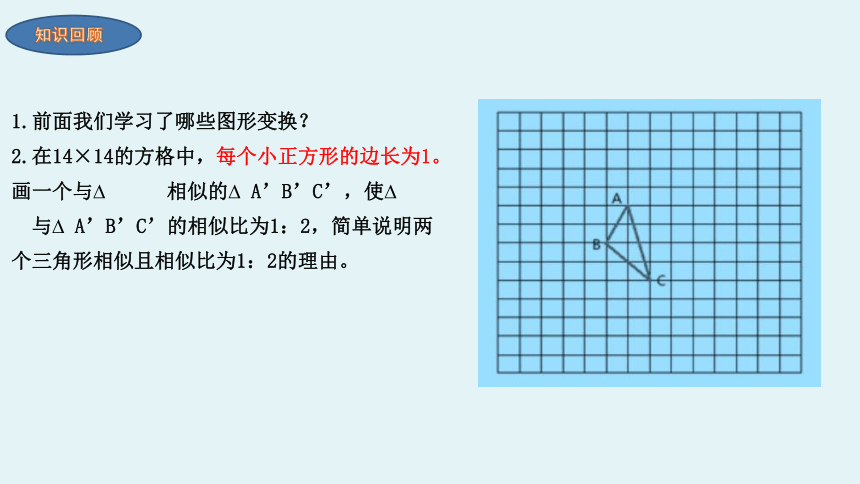
1.前面我们学习了哪些图形变换?
2.在14×14的方格中,每个小正方形的边长为1。画一个与 相似的 A’B’C’,使 与 A’B’C’的相似比为1:2,简单说明两个三角形相似且相似比为1:2的理由。
精彩展示
思考交流
1.在作业中,你能作出多少个符合题意的三角形呢?所作出来的三角形之间有什么关系呢?
2.你所做的这个三角形与原三角形之间有没有通过轴对称、平移或旋转变换得到的呢?为什么?
3.如果这个三角形没有在网格当中,还想把它放大,使放大前后图形的对应线段之比仍为1:2,
你刚才的方法还适用吗?
请欣赏如下图形的变换:放映机,将图片由近及远投映,
组成了一组大小不同、形状相同的图形。
情景感悟
在放映图片的过程中,图片在发生怎样的变化?
观察思考
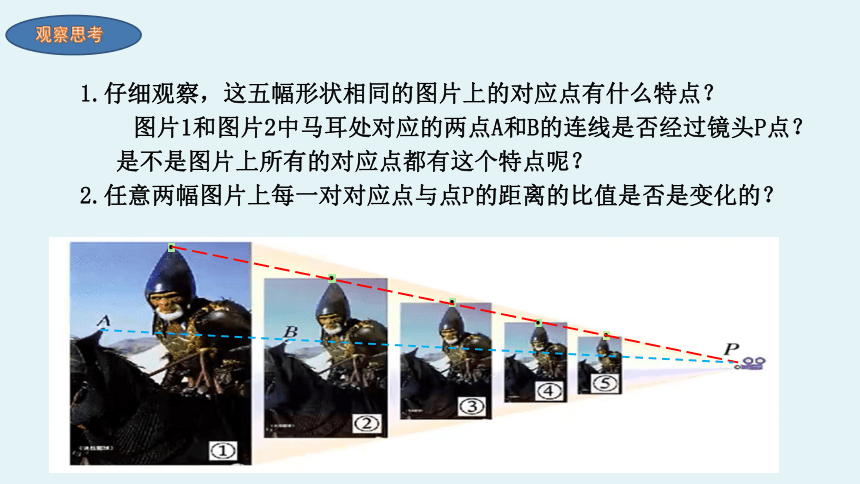
1.仔细观察,这五幅形状相同的图片上的对应点有什么特点?
图片1和图片2中马耳处对应的两点A和B的连线是否经过镜头P点?
是不是图片上所有的对应点都有这个特点呢?
2.任意两幅图片上每一对对应点与点P的距离的比值是否是变化的?
请同学们继续观察方格纸中的两个三角形,你发现每个图中的两个三角形各对应点是否具有刚才的特点?
继续观察思考
你能试着说一说什么是位似三角形吗?试着给出位似多边形的定义。
如果两个相似多边形,每组对应点的连线都经过同一点O,且对应点与点0的距离之比都相等,满足OA’=K,
那么这样的两个多边形叫做位似多边形(homothetic polygons)
这个点O叫做位似中心(homothetic center).
k,就是这两个相似多边形的相似比.
建立概念
1.位似图形是相似图形,具备相似图形的所有性质
探索性质
2.位似图形上任意一对对应点的连线交于一点,且每对对应点到位
似中心的距离之比等于相似比.
3.位似图形中的对应线段平行(或在一条直线上)
继续观察六组位似图形,思考在各组图形中,位似图形的位似中心与位似图形的每对对应点有几种位置关系?位似中心的位置应该确定在哪里?位似图形的对应线段有什么关系?
判断下面的相似图形是不是位似图形?说明理由。
应用概念
思考交流
位似图形和相似图形有怎样的关系?
前面这个三角形没有在网格当中,还想把它放大,使放大前后对应线段的比为1︰2,
你现在有放大三角形的方法了吗?试着总结一下。
解决问题
1---确定位似中心
2---画出图形各顶点的对应点
3---作出图形
将下面这个图形放大,你行吗?
活学活用
试试看
活学活用
利用铅笔和橡皮筋将下面图形放大。
大家仔细研究这样做可行吗?简单说明其中的原理。
试试看
通过本节课的学习,你学到了哪些内容?
在解决问题的过程中,掌握了那些本领
需要提醒大家注意什么呢?
畅所欲言
1.判断正误:
(1) 位似多边形一定是相似多边形。( )
(2) 相似多边形一定是位似多边形. ( )
(3) 两个位似多边形每一对对应点到位似中心的距离之比为2︰3,则两个多边形的面积之比为4︰9。( )
(4) 两个位似多边形的对应边互相平行或在同一直线上。( )
2. 如图,△DEF是由△ABC经过位似变换得到的,点O是位似中心,
D、E、F分别是OA、OB、OC的中点,则△DEF与△ABC的面积比是( )
1:2 B. 1:4 C. 1:5 D. 1:6
3.如图,四边形ABCD与四边形AEFG是位似图形,且AC:AF=2:3,
则下列结论不正确的是( )
A.四边形ABCD与四边形AEFG是相似图形 B.AD与AE的比是2:3
C.四边形ABCD与四边形AEFG的周长比是2:3
D.四边形ABCD与四边形AEFG的面积比是4:9
4. 如图所示的图形是由12个有公共顶点О的直角三角形拼成的,
∠AOB=∠BOC=…=∠LOM = 30°.图中△ABO的位似图形是( )
A. △BCO B. △FGO C. △GHO D. △HIO
课堂检测
小明要在三角形木板ABC上锯下一个一边在AB边上的面积最大的正方形,它采用了以下方法划线:
(1)在边AC上取一点G,作GD⊥AB,垂足为点D,以GD为一边在△ABC内作正方形GDEF;
(2)连接AF并延长,交BC于点F’;
(3)过点F'作AB的平行线,交AC于点G',分别过G',F’作AB的垂线,垂足为点D',E'.所得到的四边形G'D'EF就是满足条件的正方形.
想一想:小明的做法有道理吗
将你的想法梳理出来,并思考这种方法在生活当中能够帮助你解决什么问题.用文字梳理出来,与大家共享。
布置作业
路漫漫其修远兮,吾将上下而求索!
Then End
第九章第九节利用位似放缩图形
知识回顾
1.前面我们学习了哪些图形变换?
2.在14×14的方格中,每个小正方形的边长为1。画一个与 相似的 A’B’C’,使 与 A’B’C’的相似比为1:2,简单说明两个三角形相似且相似比为1:2的理由。
精彩展示
思考交流
1.在作业中,你能作出多少个符合题意的三角形呢?所作出来的三角形之间有什么关系呢?
2.你所做的这个三角形与原三角形之间有没有通过轴对称、平移或旋转变换得到的呢?为什么?
3.如果这个三角形没有在网格当中,还想把它放大,使放大前后图形的对应线段之比仍为1:2,
你刚才的方法还适用吗?
请欣赏如下图形的变换:放映机,将图片由近及远投映,
组成了一组大小不同、形状相同的图形。
情景感悟
在放映图片的过程中,图片在发生怎样的变化?
观察思考
1.仔细观察,这五幅形状相同的图片上的对应点有什么特点?
图片1和图片2中马耳处对应的两点A和B的连线是否经过镜头P点?
是不是图片上所有的对应点都有这个特点呢?
2.任意两幅图片上每一对对应点与点P的距离的比值是否是变化的?
请同学们继续观察方格纸中的两个三角形,你发现每个图中的两个三角形各对应点是否具有刚才的特点?
继续观察思考
你能试着说一说什么是位似三角形吗?试着给出位似多边形的定义。
如果两个相似多边形,每组对应点的连线都经过同一点O,且对应点与点0的距离之比都相等,满足OA’=K,
那么这样的两个多边形叫做位似多边形(homothetic polygons)
这个点O叫做位似中心(homothetic center).
k,就是这两个相似多边形的相似比.
建立概念
1.位似图形是相似图形,具备相似图形的所有性质
探索性质
2.位似图形上任意一对对应点的连线交于一点,且每对对应点到位
似中心的距离之比等于相似比.
3.位似图形中的对应线段平行(或在一条直线上)
继续观察六组位似图形,思考在各组图形中,位似图形的位似中心与位似图形的每对对应点有几种位置关系?位似中心的位置应该确定在哪里?位似图形的对应线段有什么关系?
判断下面的相似图形是不是位似图形?说明理由。
应用概念
思考交流
位似图形和相似图形有怎样的关系?
前面这个三角形没有在网格当中,还想把它放大,使放大前后对应线段的比为1︰2,
你现在有放大三角形的方法了吗?试着总结一下。
解决问题
1---确定位似中心
2---画出图形各顶点的对应点
3---作出图形
将下面这个图形放大,你行吗?
活学活用
试试看
活学活用
利用铅笔和橡皮筋将下面图形放大。
大家仔细研究这样做可行吗?简单说明其中的原理。
试试看
通过本节课的学习,你学到了哪些内容?
在解决问题的过程中,掌握了那些本领
需要提醒大家注意什么呢?
畅所欲言
1.判断正误:
(1) 位似多边形一定是相似多边形。( )
(2) 相似多边形一定是位似多边形. ( )
(3) 两个位似多边形每一对对应点到位似中心的距离之比为2︰3,则两个多边形的面积之比为4︰9。( )
(4) 两个位似多边形的对应边互相平行或在同一直线上。( )
2. 如图,△DEF是由△ABC经过位似变换得到的,点O是位似中心,
D、E、F分别是OA、OB、OC的中点,则△DEF与△ABC的面积比是( )
1:2 B. 1:4 C. 1:5 D. 1:6
3.如图,四边形ABCD与四边形AEFG是位似图形,且AC:AF=2:3,
则下列结论不正确的是( )
A.四边形ABCD与四边形AEFG是相似图形 B.AD与AE的比是2:3
C.四边形ABCD与四边形AEFG的周长比是2:3
D.四边形ABCD与四边形AEFG的面积比是4:9
4. 如图所示的图形是由12个有公共顶点О的直角三角形拼成的,
∠AOB=∠BOC=…=∠LOM = 30°.图中△ABO的位似图形是( )
A. △BCO B. △FGO C. △GHO D. △HIO
课堂检测
小明要在三角形木板ABC上锯下一个一边在AB边上的面积最大的正方形,它采用了以下方法划线:
(1)在边AC上取一点G,作GD⊥AB,垂足为点D,以GD为一边在△ABC内作正方形GDEF;
(2)连接AF并延长,交BC于点F’;
(3)过点F'作AB的平行线,交AC于点G',分别过G',F’作AB的垂线,垂足为点D',E'.所得到的四边形G'D'EF就是满足条件的正方形.
想一想:小明的做法有道理吗
将你的想法梳理出来,并思考这种方法在生活当中能够帮助你解决什么问题.用文字梳理出来,与大家共享。
布置作业
路漫漫其修远兮,吾将上下而求索!
Then End
