鲁教版(五四制)八年级下册9.3相似多边形课件(共36张PPT)
文档属性
| 名称 | 鲁教版(五四制)八年级下册9.3相似多边形课件(共36张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 8.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-28 09:38:37 | ||
图片预览






文档简介
(共36张PPT)
9.3相似多边形
在刚刚落下帷幕的冬奥会上,中国选手谷爱凌在自由式滑雪决赛中,夺得金牌,实现了历史性突破。
脊背上的中国龙 雪场上的花木兰
视频中的国旗和我们生活中的国旗形状相同吗?大小呢?
学习目标
(1)经历相似多边形概念的形成过程,了解相似多边形的含义。
(2)在探索相似多边形本质特征的过程中,进一步发展学生观察、操作、归纳、类比等多方面的能力提高学生的数学思维水平.
3)使学生体会团队合作精神,充分认识数学与人类生活的密切联系,体验数学活动充满探索与创造.
第2页
探究活动1:
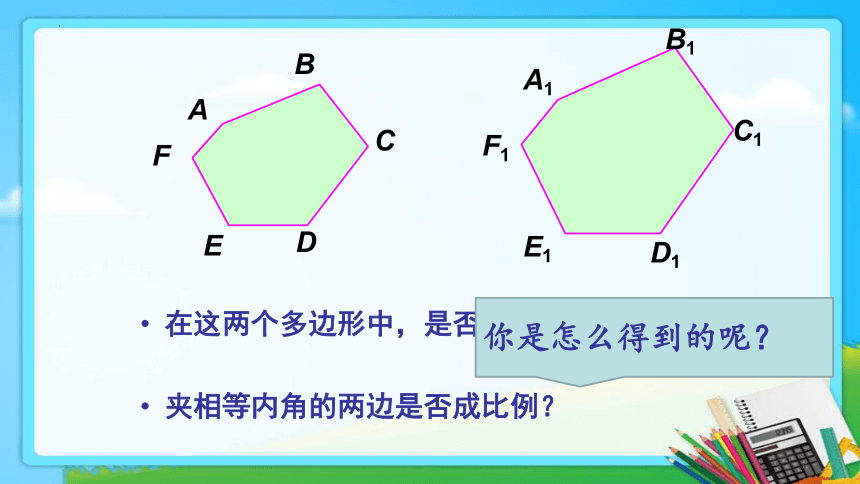
在这两个多边形中,是否有相等的内角?
夹相等内角的两边是否成比例?
A
B
C
D
E
F
A1
B1
C1
D1
E1
F1
你是怎么得到的呢?
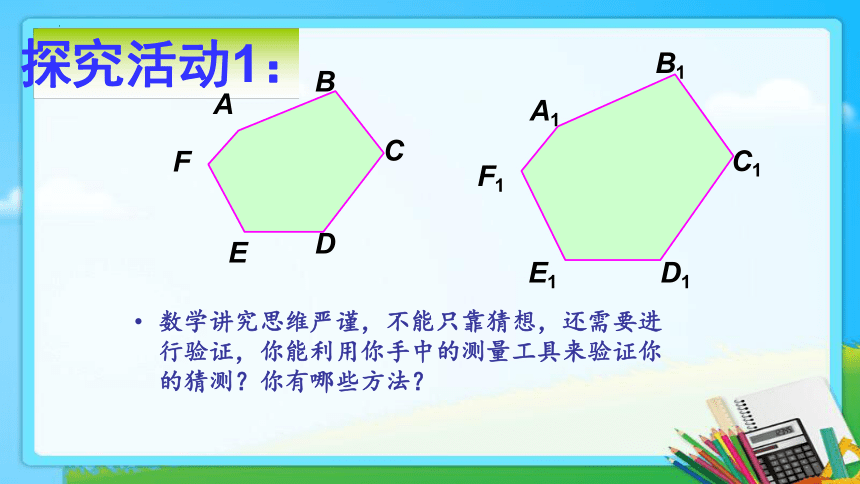
数学讲究思维严谨,不能只靠猜想,还需要进行验证,你能利用你手中的测量工具来验证你的猜测?你有哪些方法?
探究活动1:
A
B
C
D
E
F
A1
B1
C1
D1
E1
F1
(1)
B
C
D
E
F
A
B1
C1
D1
E1
F1
A1
(2)
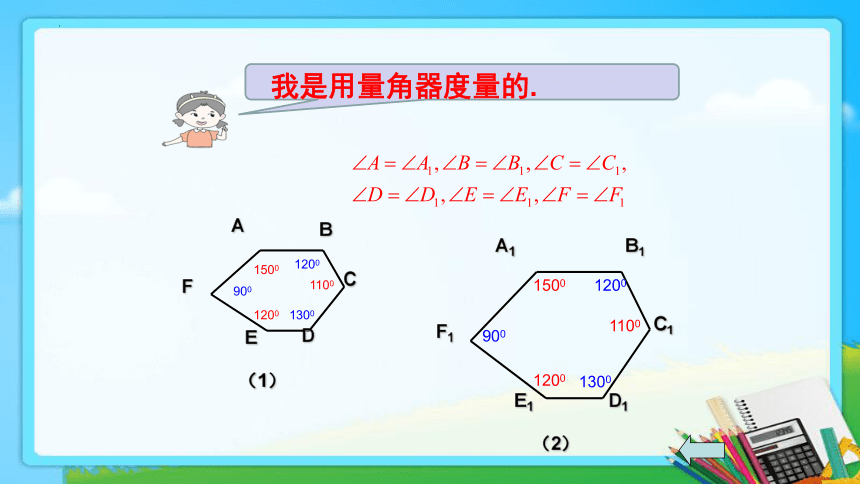
900
1200
900
1500
1200
1300
1100
1500
1200
1200
1300
1100
我是用量角器度量的.
B
C
D
E
F
A
B1
C1
D1
E1
F1
A1
B
C
D
E
F
A
B
C
D
E
F
A
B
C
D
E
F
A
我是叠合法操作的.
(1)
B
C
D
E
F
A
B1
C1
D1
E1
F1
A1
(2)
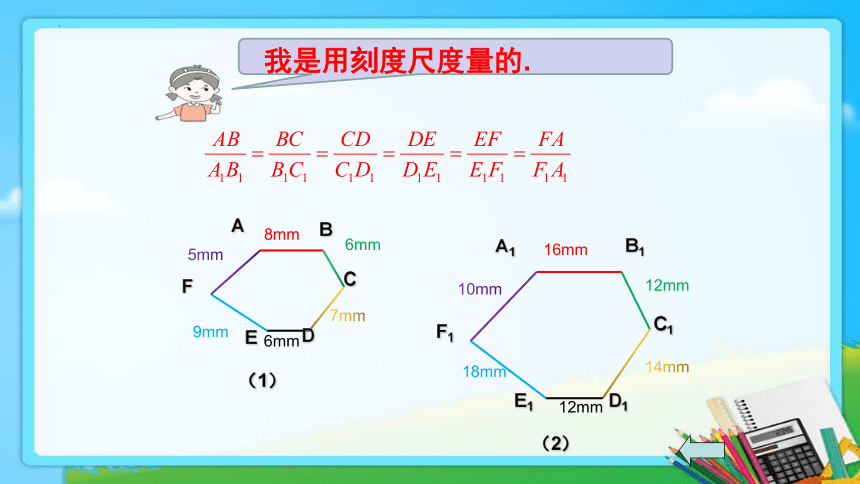
12mm
18mm
16mm
6mm
8mm
10mm
5mm
9mm
7mm
6mm
14mm
12mm
我是用刻度尺度量的.
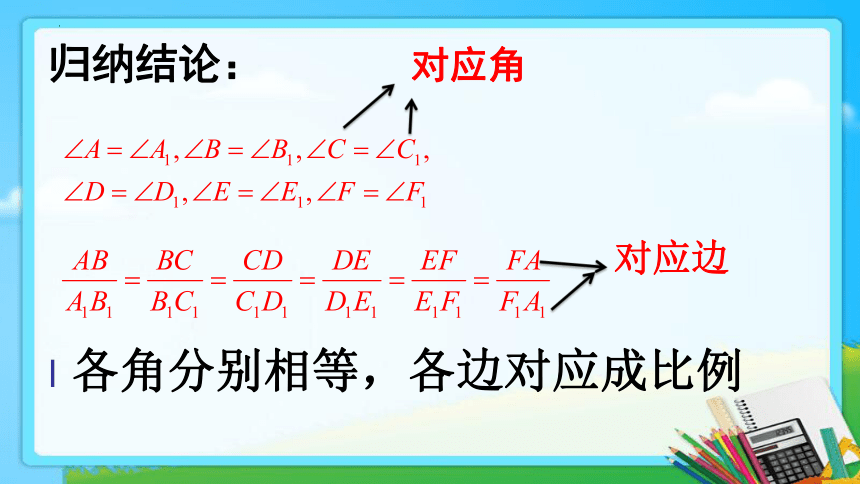
归纳结论:
各角分别相等,各边对应成比例
对应角
对应边
1、_____________________的两个多边形叫做 相似多边形.
注意:1.相似符号“∽ ”读作“相似于”。
2.对应顶点的字母写在对应的位置上。
获得新知
2表示方法:六边形ABCDEF_______________
各角分别相等、各边成比例
∽六边形A1B1C1D1E1F1
A
B
C
D
E
F
2
3
1
A1
B1
C1
D1
E1
F1
4
6
2
3、相似多边形_________ 叫做相似比.
对应边的比
注意:相似比与叙述的顺序的有关。
这两个图形是全等图形。
第26页
若相似比k =1 ,相似图形有什么关系?
全等必然相似,相似不一定全等,全等是相似的特殊形式。
如果两个多边形相似,那么它们的对应角有什么关系?对应边呢?
对应角相等,对应边成比例.
作用:常用来求相似多边形中未知的边的长度和角的度数.
相似多边形的性质:
1.图中每组两个矩形相似吗?说说你的理由.
小试牛刀
2、五边形ABCDE∽五边形 A B C D E ,则
∠ E=__ ,∠ A =__,
C D =__
五边形A B C D E 与五边形ABCDE的相似比为__
118°
A
E
D
C
B
3
2
6
80°
A
E
D
C
B
G
.
80°
118°
4
2:1
3、两个相似多边形的最长边分别为10cm和20cm,其中一个多边形的最短边为5cm,则另一个多边形的最短边为______。
10cm或2.5cm
4. 如图所示的两个五边形相似,求未知边a、b、c、d的长度.
5
3
2
c
d
7.5
b
a
6
9
解:由图示: 可知两图形的相似比为:
b = 4.5
a = 3
c = 4
d = 6
(一)思考:
在我们学习过的图形中,哪些图形是相似多边形呢?
(4)任意两个正n边形相似吗?
(1)任意两个等边三角形相似吗?
(2)任意两个正方形相似吗?
探究活动2:
(3)任意两个正五边形相似吗?
(1)正三角形ABC与正三角形DEF相似吗?
解:(1)相似。由于正三角形每个角都等于600,所以∠A=∠D= 600,∠B=∠E= 600,∠C=∠F= 600;
(1)
B
C
D
E
F
A
由于正三角形三边都相等,所以
(2)正方形ABCD与正方形EFGH相似吗?
B
C
D
E
F
A
(2)
H
G
解:(2)相似。由于正方形每个角都是直角,所以∠A=∠E= 900, ∠B=∠F= 900, ∠C=∠G= 900, ∠D=∠H= 900;
由于正方形四边相等,所以
(3)任意两个正五边形相似吗 为什么
你能得出一个一般的结论吗
……
任意两个边数相等的正多边形都相似。
归纳总结:
探究活动2:
(二)思考:
任意的两个菱形是否相似?为什么?
四条边成比例,但四个角不一定对应相等,所以任意两个菱形不一定相似。
探究活动2:
(三)思考:
任意的两个矩形是否相似?为什么?
四个角对应相等,但四条边不一定成比例,所以任意两个矩形不一定相似。
注意判断两个多边形相似的条件:
1. 对应角相等
2. 对应边成比例
两个条件缺一不可哟!
做一做
一块长3m、宽1.5m的矩形黑板如下图所示,镶在其外围的木质边框宽7.5cm。边框的内外边缘所成的矩形相似吗?为什么?
3m
1.5m
A
B
C
D
E
F
G
H
(3+0.075××2)m
(1.5+0.075××2)m
直观有时是不可靠的
实践出真知
1.如图,矩形 ABCD ∽ 矩形 EFGH,它们的相似比是2 ∶3,已知 AB = 3 cm,BC = 5 cm,求 EF,FG 的长.
巩固练习
2、如图,四边形ABCD和EFGH相似,求角α,β的大小和EH的长度x
D
A
B
C
18cm
21cm
78°
83°
β
24cm
G
E
F
H
α
x
118°
巩固练习
3.如图,一个矩形广场的长为 60 m,宽为40 m,广场内两条纵向小路的宽均为1.5 m,如果设两条横向小路的宽都为 x m,那么当 x 为多少时,小路内外边缘所围成的两个矩形相似?
巩固练习
拓展提高:
如图,在长为8 cm、宽为4 cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下的矩形的面积是( )
我总结 我提高
说 我 所 获
相似多边形
判断两个多边形是否相似
解决实际问题
相似比
对应角相等 对应边成比例
两个定义
一个性质
两种应用
1、如图所示的两个矩形相似吗?为什么?如果相似,相似比是多少?
G
F
E
H
1.5
1
A
D
C
B
3
2
2、如图所示的相似四边形中,求未知边x、y的长度和角α的大小。
770
12
y
x
6
7
8
α
课堂检测
3 如图所示的两个五边形相似,求a,b,c,d的值.
4.若一个三角形的三边之比为3:5:7,与它相似的三角形的最长边的长为21,则最短边的长为( )
A.15 B.10
C.9 D.3
有志者,事竟成,破釜沉舟,百二秦关终属楚;
苦心人,天不负,卧薪尝胆,三千越甲可吞吴。---蒲松龄
-----
寄语
9.3相似多边形
在刚刚落下帷幕的冬奥会上,中国选手谷爱凌在自由式滑雪决赛中,夺得金牌,实现了历史性突破。
脊背上的中国龙 雪场上的花木兰
视频中的国旗和我们生活中的国旗形状相同吗?大小呢?
学习目标
(1)经历相似多边形概念的形成过程,了解相似多边形的含义。
(2)在探索相似多边形本质特征的过程中,进一步发展学生观察、操作、归纳、类比等多方面的能力提高学生的数学思维水平.
3)使学生体会团队合作精神,充分认识数学与人类生活的密切联系,体验数学活动充满探索与创造.
第2页
探究活动1:
在这两个多边形中,是否有相等的内角?
夹相等内角的两边是否成比例?
A
B
C
D
E
F
A1
B1
C1
D1
E1
F1
你是怎么得到的呢?
数学讲究思维严谨,不能只靠猜想,还需要进行验证,你能利用你手中的测量工具来验证你的猜测?你有哪些方法?
探究活动1:
A
B
C
D
E
F
A1
B1
C1
D1
E1
F1
(1)
B
C
D
E
F
A
B1
C1
D1
E1
F1
A1
(2)
900
1200
900
1500
1200
1300
1100
1500
1200
1200
1300
1100
我是用量角器度量的.
B
C
D
E
F
A
B1
C1
D1
E1
F1
A1
B
C
D
E
F
A
B
C
D
E
F
A
B
C
D
E
F
A
我是叠合法操作的.
(1)
B
C
D
E
F
A
B1
C1
D1
E1
F1
A1
(2)
12mm
18mm
16mm
6mm
8mm
10mm
5mm
9mm
7mm
6mm
14mm
12mm
我是用刻度尺度量的.
归纳结论:
各角分别相等,各边对应成比例
对应角
对应边
1、_____________________的两个多边形叫做 相似多边形.
注意:1.相似符号“∽ ”读作“相似于”。
2.对应顶点的字母写在对应的位置上。
获得新知
2表示方法:六边形ABCDEF_______________
各角分别相等、各边成比例
∽六边形A1B1C1D1E1F1
A
B
C
D
E
F
2
3
1
A1
B1
C1
D1
E1
F1
4
6
2
3、相似多边形_________ 叫做相似比.
对应边的比
注意:相似比与叙述的顺序的有关。
这两个图形是全等图形。
第26页
若相似比k =1 ,相似图形有什么关系?
全等必然相似,相似不一定全等,全等是相似的特殊形式。
如果两个多边形相似,那么它们的对应角有什么关系?对应边呢?
对应角相等,对应边成比例.
作用:常用来求相似多边形中未知的边的长度和角的度数.
相似多边形的性质:
1.图中每组两个矩形相似吗?说说你的理由.
小试牛刀
2、五边形ABCDE∽五边形 A B C D E ,则
∠ E=__ ,∠ A =__,
C D =__
五边形A B C D E 与五边形ABCDE的相似比为__
118°
A
E
D
C
B
3
2
6
80°
A
E
D
C
B
G
.
80°
118°
4
2:1
3、两个相似多边形的最长边分别为10cm和20cm,其中一个多边形的最短边为5cm,则另一个多边形的最短边为______。
10cm或2.5cm
4. 如图所示的两个五边形相似,求未知边a、b、c、d的长度.
5
3
2
c
d
7.5
b
a
6
9
解:由图示: 可知两图形的相似比为:
b = 4.5
a = 3
c = 4
d = 6
(一)思考:
在我们学习过的图形中,哪些图形是相似多边形呢?
(4)任意两个正n边形相似吗?
(1)任意两个等边三角形相似吗?
(2)任意两个正方形相似吗?
探究活动2:
(3)任意两个正五边形相似吗?
(1)正三角形ABC与正三角形DEF相似吗?
解:(1)相似。由于正三角形每个角都等于600,所以∠A=∠D= 600,∠B=∠E= 600,∠C=∠F= 600;
(1)
B
C
D
E
F
A
由于正三角形三边都相等,所以
(2)正方形ABCD与正方形EFGH相似吗?
B
C
D
E
F
A
(2)
H
G
解:(2)相似。由于正方形每个角都是直角,所以∠A=∠E= 900, ∠B=∠F= 900, ∠C=∠G= 900, ∠D=∠H= 900;
由于正方形四边相等,所以
(3)任意两个正五边形相似吗 为什么
你能得出一个一般的结论吗
……
任意两个边数相等的正多边形都相似。
归纳总结:
探究活动2:
(二)思考:
任意的两个菱形是否相似?为什么?
四条边成比例,但四个角不一定对应相等,所以任意两个菱形不一定相似。
探究活动2:
(三)思考:
任意的两个矩形是否相似?为什么?
四个角对应相等,但四条边不一定成比例,所以任意两个矩形不一定相似。
注意判断两个多边形相似的条件:
1. 对应角相等
2. 对应边成比例
两个条件缺一不可哟!
做一做
一块长3m、宽1.5m的矩形黑板如下图所示,镶在其外围的木质边框宽7.5cm。边框的内外边缘所成的矩形相似吗?为什么?
3m
1.5m
A
B
C
D
E
F
G
H
(3+0.075××2)m
(1.5+0.075××2)m
直观有时是不可靠的
实践出真知
1.如图,矩形 ABCD ∽ 矩形 EFGH,它们的相似比是2 ∶3,已知 AB = 3 cm,BC = 5 cm,求 EF,FG 的长.
巩固练习
2、如图,四边形ABCD和EFGH相似,求角α,β的大小和EH的长度x
D
A
B
C
18cm
21cm
78°
83°
β
24cm
G
E
F
H
α
x
118°
巩固练习
3.如图,一个矩形广场的长为 60 m,宽为40 m,广场内两条纵向小路的宽均为1.5 m,如果设两条横向小路的宽都为 x m,那么当 x 为多少时,小路内外边缘所围成的两个矩形相似?
巩固练习
拓展提高:
如图,在长为8 cm、宽为4 cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下的矩形的面积是( )
我总结 我提高
说 我 所 获
相似多边形
判断两个多边形是否相似
解决实际问题
相似比
对应角相等 对应边成比例
两个定义
一个性质
两种应用
1、如图所示的两个矩形相似吗?为什么?如果相似,相似比是多少?
G
F
E
H
1.5
1
A
D
C
B
3
2
2、如图所示的相似四边形中,求未知边x、y的长度和角α的大小。
770
12
y
x
6
7
8
α
课堂检测
3 如图所示的两个五边形相似,求a,b,c,d的值.
4.若一个三角形的三边之比为3:5:7,与它相似的三角形的最长边的长为21,则最短边的长为( )
A.15 B.10
C.9 D.3
有志者,事竟成,破釜沉舟,百二秦关终属楚;
苦心人,天不负,卧薪尝胆,三千越甲可吞吴。---蒲松龄
-----
寄语
