《空间向量》专题1 基本概念 学案(Word版含答案)
文档属性
| 名称 | 《空间向量》专题1 基本概念 学案(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 367.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-28 07:06:52 | ||
图片预览




文档简介
《空间向量》专题1-1 基本概念
(4套,7页,含答案)
知识点:
空间向量的概念: 在空间中具有大小和方向的量叫做空间向量 注:⑴空间的一个平移就是一个向量 ⑵向量一般用有向线段表示同向等长的有向线段表示同一或相等的向量 ⑶空间的两个向量可用同一平面内的两条有向线段来表示 标注空间坐标点: 空间直角坐标系的x轴是横轴(对应为横坐标),y轴是纵轴(对应为纵轴),z轴是竖轴(对应为竖坐标). (1)X、Y、Z轴。两两之间要垂直; (2)先从正方体、长方体开始训练标注坐标点; (3)不容易标注的几何体,可以先画出其俯视图,标注俯视图的坐标点(x,y),然后再标注立体坐标; (4)涉两点中点的坐标,用中点公式比较方便。,,。
典型例题:
已知正方体棱长为1,试建立恰当的坐标系并表示出各个顶点的坐标.([endnoteRef:0]) [0: 答案:略;]
在空间直角坐标系中,在Ox轴上的点P1的坐标特点为 ,在Oy轴上的点的坐标特点为 ,
在Oz轴上的点的坐标特点为 ,在xOy平面上的点的坐标特点为 ,
在yOz平面上的点的坐标特点为 ,在xOz平面上的点的坐标特点为 [endnoteRef:1] . [1: 答案:,,,,;]
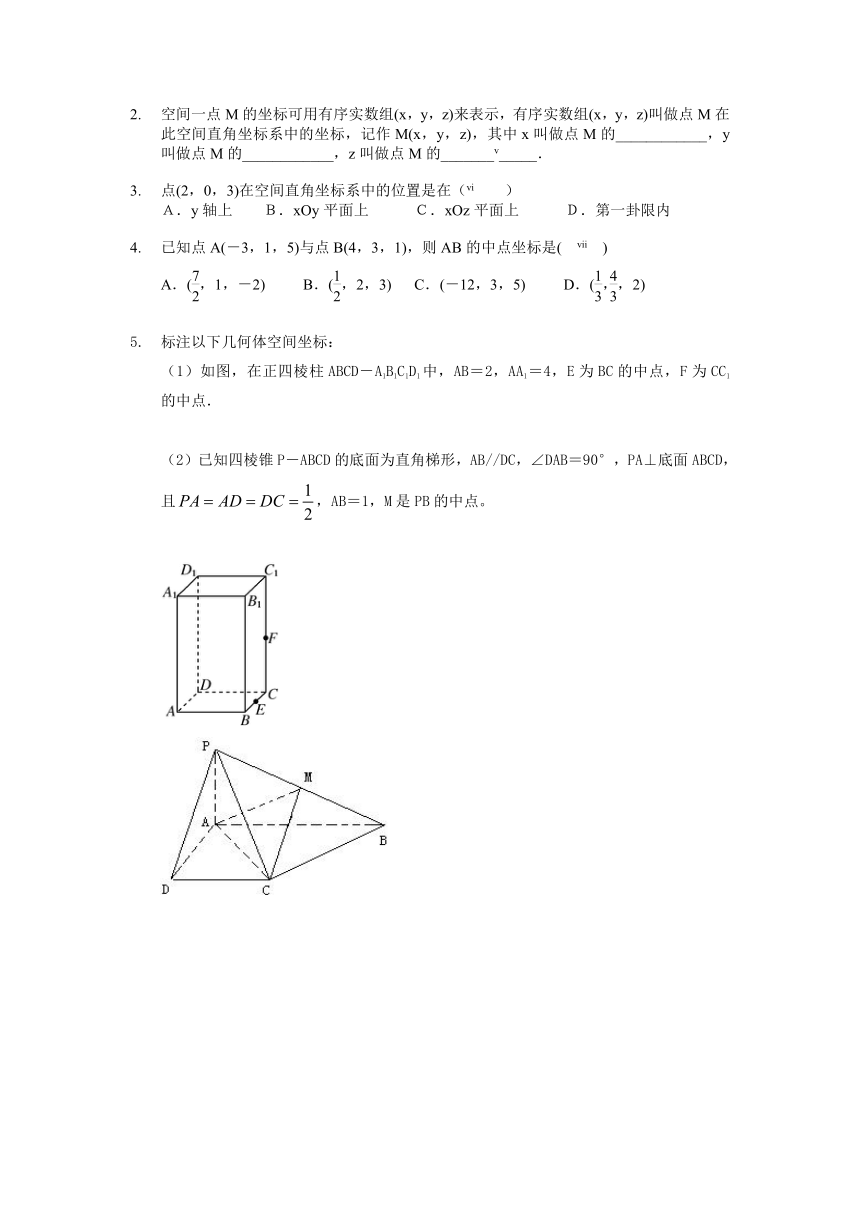
如图,三棱柱ABC-A1B1C1中,所有棱长都为2,侧棱AA1⊥底面ABC,建立适当坐标系写出各顶点的坐标.[endnoteRef:2]
[2: 答案:作图略;
[分析] 题中给出了三棱柱的棱长,要求各顶点的坐标,可以作出两两垂直的三条线分别为x、y、z轴建立空间直角坐标系,然后确定各点坐标.
[解析] 取AC的中点O和A1C1的中点O1,可得BO⊥AC,分别以OB、OC、OO1所在直线为x、y、z轴建立空间直角坐标系.
因为三棱柱各棱长均为2,所以OA=OC=1,OB=,
可得A(0,-1,0),B(,0,0),C(0,1,0),A1(0,-1,2),B1(,0,2),C1(0,1,2).
]
随堂练习:
如图所示,为了确定空间点的位置,我们建立空间直角坐标系:以单位正方体为载体,以O为原点,分别以射线OA、OC、OD′的方向为正方向,以线段OA、OC、OD′的长为单位长,建立三条数轴:x轴、y轴、z轴,这时我们说建立了一个______________________________,其中点O叫做________________,x轴、y轴、z轴叫做________________,通过每两个坐标轴的平面叫做________________,分别称为__________________________,通常建立的坐标系为右手直角坐标系,即________指向x轴的正方向,________指向y轴的正方向,________[endnoteRef:3]指向z轴的正方向.
[3: 答案:空间直角坐标系Oxyz 坐标原点 坐标轴 坐标平面 xOy平面、yOz平面、zOx平面 右手拇指 食指 中指;]
空间一点M的坐标可用有序实数组(x,y,z)来表示,有序实数组(x,y,z)叫做点M在此空间直角坐标系中的坐标,记作M(x,y,z),其中x叫做点M的____________,y叫做点M的____________,z叫做点M的_______[endnoteRef:4]_____. [4: 答案:横坐标 纵坐标 竖坐标;]
点(2,0,3)在空间直角坐标系中的位置是在([endnoteRef:5] )
A.y轴上 B.xOy平面上 C.xOz平面上 D.第一卦限内 [5: 答案:C;]
已知点A(-3,1,5)与点B(4,3,1),则AB的中点坐标是( [endnoteRef:6] )
A.(,1,-2) B.(,2,3) C.(-12,3,5) D.(,,2) [6: 答案:B;]
标注以下几何体空间坐标:
(1)如图,在正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=4,E为BC的中点,F为CC1的中点.
(2)已知四棱锥P-ABCD的底面为直角梯形,AB//DC,∠DAB=90°,PA⊥底面ABCD,且,AB=1,M是PB的中点。
知识点:
空间两点的距离公式: A,B,则A、B两点之间的距离为: 向量的模: 设,则有向线段的长度叫做向量的长度或模,记作:. (用到常用的向量模与向量之间的转化:) 点与坐标轴的距离: A,A与Z轴的距离:;与Y轴的距离:; 与X轴的距离:; 点与坐标平面的距离: A,A与平面的距离:;与平面的距离:; 与平面的距离:; 初学的时候理解一下,理解之后直接记结论,规律其实很容易看到的。
典型例题:
已知两点,,此两点间的距离为( [endnoteRef:7] )
A. B. C. D. [7: 答案:A;]
点P(2,3,5)到平面xOy的距离为 [endnoteRef:8] . [8: 答案:5;]
随堂练习:
点M(4,-3,5)到原点的距离d= ,到z轴的距离d= [endnoteRef:9] . [9: 答案:,;]
点A在z轴上,它到点(3,2,1)的距离是,则点A的坐标是( [endnoteRef:10] )
A.(0,0,-1) B.(0,1,1) C.(0,0,1) D.(0,0,13) [10: 答案:C;
[解析] 设A(0,0,c),则=,解得c=1.所以点A的坐标为(0,0,1).]
在平行六面体ABCD-A′B′C′D中,与向量的模相等的向量有( [endnoteRef:11] )
A.7个 B.3个 C.5个 D.6个 [11: 答案:A;
解析: ||=||=||=|C|=|B|=||=||=||.]
知识点:
对称点: 关于x轴的对称点: x坐标不变,y,z为相反数; 关于y轴的对称点: y坐标不变,x,z为相反数; 关于z轴的对称点: z坐标不变,x,y为相反数; 关于平面xOy的对称点: x,y坐标不变,z为相反数; 关于平面yOz的对称点: y,z坐标不变,x为相反数; 关于平面zOx的对称点: z,x坐标不变,y为相反数; 关于原点的对称点: x,y,z均为相反数; 关于其他点对称,设未知数,用中点公式;
典型例题3:
点P(-3,2,-1)关于平面xOy的对称点是 ,关于平面yOz的对称点是 ,
关于平面zOx的对称点是 ,关于x轴的对称点是 ,
关于y轴的对称点是 ,关于z轴的对称点是 .
关于原点的对称点为 ,关于点Q(2,0,-4)的对称点是 [endnoteRef:12] . [12: 答案:,,,,,., ; ]
随堂练习3:
点P(-1,2,3)关于平面xOy的对称点是 ,关于平面yOz的对称点是 ,关于平面zOx的对称点是 ,关于x轴的对称点是 ,
关于y轴的对称点是 ,关于z轴的对称点是 .
关于原点的对称点为 ,关于点Q(2,0,-4)的对称点是[endnoteRef:13] [13: 答案:(-1,2,-3),(1,2,3),(-1,-2,3),(-1,-2,-3),(1,2,-3),(1,-2,3),(1,-2,-3),(5,-2,-11);]
知识点4:
坐标运算: ,,则
随堂练习:
若向量,则______[endnoteRef:14]______。 [14: 答案:;
,]
《空间向量》专题1-2 基本概念
在空间直角坐标系中,下列说法中:
①在x轴上的点的坐标一定是(0,b,c);
②在yOz平面上的点的坐标一定可写成(0,b,c);
③在z轴上的点的坐标可记作(0,0,c);
④在xOz平面上的点的坐标是(a,0,c).
其中正确说法的序号是____[endnoteRef:15]____. [15: 答案:②③④;]
在空间直角坐标系中,点P的坐标为(1,,),过点P作yOz平面的垂线PQ,
则垂足Q的坐标是_[endnoteRef:16]_____. [16: 答案:(0,,);]
如图所示,四棱锥P-ABCD的底面ABCD是边长为1的菱形,
∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=2.
试建立适当的空间直角坐标系,求出A、B、C、D、P、E的坐标.([endnoteRef:17])
[17: 答案:A(0,0,0),B(1,0,0),C(,,0),D(,,0),P(0,0,2),E(1,,0);
解 如图所示,以A为原点,以AB所在直线为x轴,AP所在直
线为z轴,过点A与xAz平面垂直的直线为y轴,建立空间直角坐标系.则相关各点的坐标分别是A(0,0,0),B(1,0,0),C(,,0),D(,,0),P(0,0,2),E(1,,0).]
已知三角形的三个顶点A(2,-1,4),B(3,2,-6),C(5,0,2).则
(1)过A点的中线长为 ;
(2)过B点的中线长为 ;
(3)过C点的中线长为 [endnoteRef:18] . [18: 答案:,,;]
给定空间直角坐标系,在x轴上找一点P,使它与点的距离为.[endnoteRef:19] [19: 答案:点坐标为或;
解:设点的坐标是,由题意,,即,
.解得或.点坐标为或. ]
若点P(x,y,z)到平面xOz与到y轴距离相等,则P点坐标满足的关系式为______[endnoteRef:20]______. [20: 答案:x2+z2-y2=0;]
在空间直角坐标系中,点A(1,2,-3)关于x轴的对称点为( [endnoteRef:21] )
A.(1,-2,-3) B.(1,-2,3) C.(1,2,3) D.(-1,2,-3) [21: 答案:B;
[两点关于x轴对称,坐标关系:横坐标相同,纵竖坐标相反.]]
点M(1,-4,3)关于点P(4,0,-3)的对称点M′的坐标是____[endnoteRef:22]____. [22: 答案:(7,4,-9);
[解析] 线段MM′的中点是点P,则M′(7,4,-9).]
已知a=(1,0,1),b=(-2,-1,1),c=(3,1,0),则|a-b+2c|等于( [endnoteRef:23] )
A.3 B.2 C. D.5 [23: 答案:A;
解析: ∵a-b+2c=(1,0,1)-(-2,-1,1)+(6,2,0)
=(3,1,0)+(6,2,0)=(9,3,0),∴|a-b+2c|=3.]
《空间向量》专题1-3 基本概念
已知正方体ABCD-A1B1C1D1,E、F、G是DD1、BD、BB1的中点,且正方体棱长为1.请建立适当坐标系,写出正方体各顶点及E、F、G的坐标.[endnoteRef:24] [24: 答案:作图略;
解
如图所示,建立空间直角坐标系,则A(1,0,0),B(1,1,0),C(0,1,0),D(0,0,0),A1(1,0,1),B1(1,1,1),C1(0,1,1),D1(0,0,1),E,F,G.
]
在空间直角坐标系中,点,过点P作平面xOy的垂线PQ,则Q的坐标为( [endnoteRef:25] )
A. B. C. D. [25: 答案:D;
]
如图所示,AF、DE分别是⊙O、⊙O1的直径,AD与两圆
所在的平面均垂直,AD=8.BC是⊙O的直径,AB=AC=6,
OE∥AD,试建立适当的空间直角坐标系,
求出点A、B、C、D、E、F的坐标.[endnoteRef:26]
[26: 答案:作图略;
解 因为AD与两圆所在的平面均垂直,OE∥AD,所以OE与两圆所在的平面也都垂直.又因为AB=AC=6,BC是圆O的直径,所以△BAC为等腰直角三角形且AF⊥BC,BC=6.
以O为原点,OB、OF、OE所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,则原点O及A、B、C、D、E、F各个点的坐标分别为O(0,0,0)、A(0,-3,0)、B(3,0,0)、C(-3,0,0)、D(0,-3,8)、E(0,0,8)、F(0,3,0).
]
在△ABC中,已知A(-1,2,3),B(2,-2,3),C(,,3),则AB边上的中线CD的长是____[endnoteRef:27]____. [27: 答案:;
[解析] 由题可知AB的中点D的坐标是D(,0,3),
由距离公式可得
|CD|==.]
已知A点坐标为(1,1,1),B(3,3,3),点P在x轴上,且 |PA|=|PB| ,则P点坐标为( [endnoteRef:28] )
A.(6,0,0) B.(6,0,1) C.(0,0,6) D(0,6,0). [28: 答案:A;]
点P(a,b,c)到坐标平面xOy的距离是( [endnoteRef:29] )
A. B.|a| C.|b| D.|c| [29: 答案:D;]
已知点A(-3,1,4),则点A关于原点的对称点的坐标为( [endnoteRef:30] )
A.(1,-3,-4) B.(-4,1,-3) C.(3,-1,-4) D.(4,-1,3) [30: 答案:C;]
点P(-3,2,1)关于Q(1,2,-3)的对称点M的坐标是__[endnoteRef:31]______. [31: 答案:(5,2,-7);]
已知A(3,4,5),B(0,2,1),O(0,0,0),若=,则C的坐标是( [endnoteRef:32] )
A. B. C. D. [32: 答案:A;
解析: =(-3,-2,-4)
=
∴C.
答案: A
]
《空间向量》专题1-4 基本概念
结晶体的基本单位称为晶胞,如图是食盐晶胞的示意图(可看成
是八个棱长为的小正方体堆积成的正方体).其中实圆 代表钠
原子,空间圆?代表氯原子.建立空间直角坐标系Oxyz后,
图中最上层中间的钠原子所在位置的坐标是( [endnoteRef:33] )
A. B.(0,0,1) C. D. [33: 答案:A;]
点P(5,0,-2)在空间直角坐标系中的位置是( [endnoteRef:34] )
A.y轴上 B.xOy平面上 C.xOz平面上 D.x轴上 [34: 答案:C;]
已知正四面体ABCD棱长为a,试建立恰当的坐标系并表示出各个顶点的坐标.([endnoteRef:35]) [35: 答案:作图略;
解析: 过A作AG垂直于平面BCD,
由于AB=AC=AD,所以G为△BCD的中心,
过G作GF∥CD,E为CD的中点,
以G为原点,,G,G分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系.
因为△BCD的边长为a,
则BE=a,GE=a,又=,所以GF=×a=a,
又BG=a,所以AG==a,
所以A,B,C,D.
]
连接平面上两点P1(x1,y1)、P2(x2,y2)的线段P1P2的中点M的坐标为,那么,已知空间中两点P1(x1,y1,z1)、P2(x2,y2,z2),线段P1P2的中点M的坐标为_____________[endnoteRef:36]_______. [36: 答案:;]
在长方体ABCD—A1B1C1D1中,|AB|=|AD|=3,
|AA1|=2,点M在A1C1上,|MC1|=2|A1M|,N在
D1C上且为D1C中点,求M、N两点间的距离.[endnoteRef:37]
[37: 答案:;
解 如图分别以AB、AD、AA1所在的直线为x轴、y轴、z轴建立空间直角坐标系.
由题意可知C(3,3,0),
D(0,3,0),∵|DD1|=|CC1|=2,∴C1(3,3,2),D1(0,3,2),∵N为CD1的中点,
∴N.
M是A1C1的三分之一分点且靠近A1点,∴M(1,1,2).
由两点间距离公式,得|MN|==.
]
在空间直角坐标系中,已知点A(1,0,2),B(1,-3,1),
点M在y轴上,且M到A与到B的距离相等,则M的坐标是____[endnoteRef:38]____. [38: 答案:(0,-1,0);
解析 设M的坐标为(0,y,0),由|MA|=|MB|得(0-1)2+(y-0)2+(0-2)2=(0-1)2+(y+3)2+(0-1)2,整理得6y+6=0,
∴y=-1,即点M的坐标为(0,-1,0).
]
空间直角坐标系中,点A(3,2,-5)到x轴的距离d等于( [endnoteRef:39] )
A. B. C. D. [39: 答案:B;
[解析] 过A作AB⊥x轴于B,则B(3,0,0),则点A到x轴的距离d=|AB|=.]
在空间直角坐标系中,点P(3,4,5)关于yOz平面的对称点的坐标为( [endnoteRef:40] )
A.(-3,4,5) B.(-3,-4,5) C.(3,-4,-5) D.(-3,4,-5) [40: 答案:A;
[两点关于平面yOz对称,坐标关系:横坐标相反,纵竖坐标相同.]
]
在空间直角坐标系中,P(2,3,4)、Q(-2,-3,-4)两点的位置关系是( [endnoteRef:41] )
A.关于x轴对称 B.关于yOz平面对称 C.关于坐标原点对称 D.以上都不对 [41: 答案:C;
[三坐标均相反时,两点关于原点对称.]]
正方体ABCD-A1B1C1D1中,点E、F分别是底面A1C1和侧面CD1的中心,若+λ=0(λ∈R),
则λ=____[endnoteRef:42]____. [42: 答案:-;
解析: 如图,连结A1C1,C1D,则E在A1C1上,F在C1D上,
易知EF綊A1D,∴=,即E-=0,∴λ=-.
答案: -
]
(4套,7页,含答案)
知识点:
空间向量的概念: 在空间中具有大小和方向的量叫做空间向量 注:⑴空间的一个平移就是一个向量 ⑵向量一般用有向线段表示同向等长的有向线段表示同一或相等的向量 ⑶空间的两个向量可用同一平面内的两条有向线段来表示 标注空间坐标点: 空间直角坐标系的x轴是横轴(对应为横坐标),y轴是纵轴(对应为纵轴),z轴是竖轴(对应为竖坐标). (1)X、Y、Z轴。两两之间要垂直; (2)先从正方体、长方体开始训练标注坐标点; (3)不容易标注的几何体,可以先画出其俯视图,标注俯视图的坐标点(x,y),然后再标注立体坐标; (4)涉两点中点的坐标,用中点公式比较方便。,,。
典型例题:
已知正方体棱长为1,试建立恰当的坐标系并表示出各个顶点的坐标.([endnoteRef:0]) [0: 答案:略;]
在空间直角坐标系中,在Ox轴上的点P1的坐标特点为 ,在Oy轴上的点的坐标特点为 ,
在Oz轴上的点的坐标特点为 ,在xOy平面上的点的坐标特点为 ,
在yOz平面上的点的坐标特点为 ,在xOz平面上的点的坐标特点为 [endnoteRef:1] . [1: 答案:,,,,;]
如图,三棱柱ABC-A1B1C1中,所有棱长都为2,侧棱AA1⊥底面ABC,建立适当坐标系写出各顶点的坐标.[endnoteRef:2]
[2: 答案:作图略;
[分析] 题中给出了三棱柱的棱长,要求各顶点的坐标,可以作出两两垂直的三条线分别为x、y、z轴建立空间直角坐标系,然后确定各点坐标.
[解析] 取AC的中点O和A1C1的中点O1,可得BO⊥AC,分别以OB、OC、OO1所在直线为x、y、z轴建立空间直角坐标系.
因为三棱柱各棱长均为2,所以OA=OC=1,OB=,
可得A(0,-1,0),B(,0,0),C(0,1,0),A1(0,-1,2),B1(,0,2),C1(0,1,2).
]
随堂练习:
如图所示,为了确定空间点的位置,我们建立空间直角坐标系:以单位正方体为载体,以O为原点,分别以射线OA、OC、OD′的方向为正方向,以线段OA、OC、OD′的长为单位长,建立三条数轴:x轴、y轴、z轴,这时我们说建立了一个______________________________,其中点O叫做________________,x轴、y轴、z轴叫做________________,通过每两个坐标轴的平面叫做________________,分别称为__________________________,通常建立的坐标系为右手直角坐标系,即________指向x轴的正方向,________指向y轴的正方向,________[endnoteRef:3]指向z轴的正方向.
[3: 答案:空间直角坐标系Oxyz 坐标原点 坐标轴 坐标平面 xOy平面、yOz平面、zOx平面 右手拇指 食指 中指;]
空间一点M的坐标可用有序实数组(x,y,z)来表示,有序实数组(x,y,z)叫做点M在此空间直角坐标系中的坐标,记作M(x,y,z),其中x叫做点M的____________,y叫做点M的____________,z叫做点M的_______[endnoteRef:4]_____. [4: 答案:横坐标 纵坐标 竖坐标;]
点(2,0,3)在空间直角坐标系中的位置是在([endnoteRef:5] )
A.y轴上 B.xOy平面上 C.xOz平面上 D.第一卦限内 [5: 答案:C;]
已知点A(-3,1,5)与点B(4,3,1),则AB的中点坐标是( [endnoteRef:6] )
A.(,1,-2) B.(,2,3) C.(-12,3,5) D.(,,2) [6: 答案:B;]
标注以下几何体空间坐标:
(1)如图,在正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=4,E为BC的中点,F为CC1的中点.
(2)已知四棱锥P-ABCD的底面为直角梯形,AB//DC,∠DAB=90°,PA⊥底面ABCD,且,AB=1,M是PB的中点。
知识点:
空间两点的距离公式: A,B,则A、B两点之间的距离为: 向量的模: 设,则有向线段的长度叫做向量的长度或模,记作:. (用到常用的向量模与向量之间的转化:) 点与坐标轴的距离: A,A与Z轴的距离:;与Y轴的距离:; 与X轴的距离:; 点与坐标平面的距离: A,A与平面的距离:;与平面的距离:; 与平面的距离:; 初学的时候理解一下,理解之后直接记结论,规律其实很容易看到的。
典型例题:
已知两点,,此两点间的距离为( [endnoteRef:7] )
A. B. C. D. [7: 答案:A;]
点P(2,3,5)到平面xOy的距离为 [endnoteRef:8] . [8: 答案:5;]
随堂练习:
点M(4,-3,5)到原点的距离d= ,到z轴的距离d= [endnoteRef:9] . [9: 答案:,;]
点A在z轴上,它到点(3,2,1)的距离是,则点A的坐标是( [endnoteRef:10] )
A.(0,0,-1) B.(0,1,1) C.(0,0,1) D.(0,0,13) [10: 答案:C;
[解析] 设A(0,0,c),则=,解得c=1.所以点A的坐标为(0,0,1).]
在平行六面体ABCD-A′B′C′D中,与向量的模相等的向量有( [endnoteRef:11] )
A.7个 B.3个 C.5个 D.6个 [11: 答案:A;
解析: ||=||=||=|C|=|B|=||=||=||.]
知识点:
对称点: 关于x轴的对称点: x坐标不变,y,z为相反数; 关于y轴的对称点: y坐标不变,x,z为相反数; 关于z轴的对称点: z坐标不变,x,y为相反数; 关于平面xOy的对称点: x,y坐标不变,z为相反数; 关于平面yOz的对称点: y,z坐标不变,x为相反数; 关于平面zOx的对称点: z,x坐标不变,y为相反数; 关于原点的对称点: x,y,z均为相反数; 关于其他点对称,设未知数,用中点公式;
典型例题3:
点P(-3,2,-1)关于平面xOy的对称点是 ,关于平面yOz的对称点是 ,
关于平面zOx的对称点是 ,关于x轴的对称点是 ,
关于y轴的对称点是 ,关于z轴的对称点是 .
关于原点的对称点为 ,关于点Q(2,0,-4)的对称点是 [endnoteRef:12] . [12: 答案:,,,,,., ; ]
随堂练习3:
点P(-1,2,3)关于平面xOy的对称点是 ,关于平面yOz的对称点是 ,关于平面zOx的对称点是 ,关于x轴的对称点是 ,
关于y轴的对称点是 ,关于z轴的对称点是 .
关于原点的对称点为 ,关于点Q(2,0,-4)的对称点是[endnoteRef:13] [13: 答案:(-1,2,-3),(1,2,3),(-1,-2,3),(-1,-2,-3),(1,2,-3),(1,-2,3),(1,-2,-3),(5,-2,-11);]
知识点4:
坐标运算: ,,则
随堂练习:
若向量,则______[endnoteRef:14]______。 [14: 答案:;
,]
《空间向量》专题1-2 基本概念
在空间直角坐标系中,下列说法中:
①在x轴上的点的坐标一定是(0,b,c);
②在yOz平面上的点的坐标一定可写成(0,b,c);
③在z轴上的点的坐标可记作(0,0,c);
④在xOz平面上的点的坐标是(a,0,c).
其中正确说法的序号是____[endnoteRef:15]____. [15: 答案:②③④;]
在空间直角坐标系中,点P的坐标为(1,,),过点P作yOz平面的垂线PQ,
则垂足Q的坐标是_[endnoteRef:16]_____. [16: 答案:(0,,);]
如图所示,四棱锥P-ABCD的底面ABCD是边长为1的菱形,
∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=2.
试建立适当的空间直角坐标系,求出A、B、C、D、P、E的坐标.([endnoteRef:17])
[17: 答案:A(0,0,0),B(1,0,0),C(,,0),D(,,0),P(0,0,2),E(1,,0);
解 如图所示,以A为原点,以AB所在直线为x轴,AP所在直
线为z轴,过点A与xAz平面垂直的直线为y轴,建立空间直角坐标系.则相关各点的坐标分别是A(0,0,0),B(1,0,0),C(,,0),D(,,0),P(0,0,2),E(1,,0).]
已知三角形的三个顶点A(2,-1,4),B(3,2,-6),C(5,0,2).则
(1)过A点的中线长为 ;
(2)过B点的中线长为 ;
(3)过C点的中线长为 [endnoteRef:18] . [18: 答案:,,;]
给定空间直角坐标系,在x轴上找一点P,使它与点的距离为.[endnoteRef:19] [19: 答案:点坐标为或;
解:设点的坐标是,由题意,,即,
.解得或.点坐标为或. ]
若点P(x,y,z)到平面xOz与到y轴距离相等,则P点坐标满足的关系式为______[endnoteRef:20]______. [20: 答案:x2+z2-y2=0;]
在空间直角坐标系中,点A(1,2,-3)关于x轴的对称点为( [endnoteRef:21] )
A.(1,-2,-3) B.(1,-2,3) C.(1,2,3) D.(-1,2,-3) [21: 答案:B;
[两点关于x轴对称,坐标关系:横坐标相同,纵竖坐标相反.]]
点M(1,-4,3)关于点P(4,0,-3)的对称点M′的坐标是____[endnoteRef:22]____. [22: 答案:(7,4,-9);
[解析] 线段MM′的中点是点P,则M′(7,4,-9).]
已知a=(1,0,1),b=(-2,-1,1),c=(3,1,0),则|a-b+2c|等于( [endnoteRef:23] )
A.3 B.2 C. D.5 [23: 答案:A;
解析: ∵a-b+2c=(1,0,1)-(-2,-1,1)+(6,2,0)
=(3,1,0)+(6,2,0)=(9,3,0),∴|a-b+2c|=3.]
《空间向量》专题1-3 基本概念
已知正方体ABCD-A1B1C1D1,E、F、G是DD1、BD、BB1的中点,且正方体棱长为1.请建立适当坐标系,写出正方体各顶点及E、F、G的坐标.[endnoteRef:24] [24: 答案:作图略;
解
如图所示,建立空间直角坐标系,则A(1,0,0),B(1,1,0),C(0,1,0),D(0,0,0),A1(1,0,1),B1(1,1,1),C1(0,1,1),D1(0,0,1),E,F,G.
]
在空间直角坐标系中,点,过点P作平面xOy的垂线PQ,则Q的坐标为( [endnoteRef:25] )
A. B. C. D. [25: 答案:D;
]
如图所示,AF、DE分别是⊙O、⊙O1的直径,AD与两圆
所在的平面均垂直,AD=8.BC是⊙O的直径,AB=AC=6,
OE∥AD,试建立适当的空间直角坐标系,
求出点A、B、C、D、E、F的坐标.[endnoteRef:26]
[26: 答案:作图略;
解 因为AD与两圆所在的平面均垂直,OE∥AD,所以OE与两圆所在的平面也都垂直.又因为AB=AC=6,BC是圆O的直径,所以△BAC为等腰直角三角形且AF⊥BC,BC=6.
以O为原点,OB、OF、OE所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,则原点O及A、B、C、D、E、F各个点的坐标分别为O(0,0,0)、A(0,-3,0)、B(3,0,0)、C(-3,0,0)、D(0,-3,8)、E(0,0,8)、F(0,3,0).
]
在△ABC中,已知A(-1,2,3),B(2,-2,3),C(,,3),则AB边上的中线CD的长是____[endnoteRef:27]____. [27: 答案:;
[解析] 由题可知AB的中点D的坐标是D(,0,3),
由距离公式可得
|CD|==.]
已知A点坐标为(1,1,1),B(3,3,3),点P在x轴上,且 |PA|=|PB| ,则P点坐标为( [endnoteRef:28] )
A.(6,0,0) B.(6,0,1) C.(0,0,6) D(0,6,0). [28: 答案:A;]
点P(a,b,c)到坐标平面xOy的距离是( [endnoteRef:29] )
A. B.|a| C.|b| D.|c| [29: 答案:D;]
已知点A(-3,1,4),则点A关于原点的对称点的坐标为( [endnoteRef:30] )
A.(1,-3,-4) B.(-4,1,-3) C.(3,-1,-4) D.(4,-1,3) [30: 答案:C;]
点P(-3,2,1)关于Q(1,2,-3)的对称点M的坐标是__[endnoteRef:31]______. [31: 答案:(5,2,-7);]
已知A(3,4,5),B(0,2,1),O(0,0,0),若=,则C的坐标是( [endnoteRef:32] )
A. B. C. D. [32: 答案:A;
解析: =(-3,-2,-4)
=
∴C.
答案: A
]
《空间向量》专题1-4 基本概念
结晶体的基本单位称为晶胞,如图是食盐晶胞的示意图(可看成
是八个棱长为的小正方体堆积成的正方体).其中实圆 代表钠
原子,空间圆?代表氯原子.建立空间直角坐标系Oxyz后,
图中最上层中间的钠原子所在位置的坐标是( [endnoteRef:33] )
A. B.(0,0,1) C. D. [33: 答案:A;]
点P(5,0,-2)在空间直角坐标系中的位置是( [endnoteRef:34] )
A.y轴上 B.xOy平面上 C.xOz平面上 D.x轴上 [34: 答案:C;]
已知正四面体ABCD棱长为a,试建立恰当的坐标系并表示出各个顶点的坐标.([endnoteRef:35]) [35: 答案:作图略;
解析: 过A作AG垂直于平面BCD,
由于AB=AC=AD,所以G为△BCD的中心,
过G作GF∥CD,E为CD的中点,
以G为原点,,G,G分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系.
因为△BCD的边长为a,
则BE=a,GE=a,又=,所以GF=×a=a,
又BG=a,所以AG==a,
所以A,B,C,D.
]
连接平面上两点P1(x1,y1)、P2(x2,y2)的线段P1P2的中点M的坐标为,那么,已知空间中两点P1(x1,y1,z1)、P2(x2,y2,z2),线段P1P2的中点M的坐标为_____________[endnoteRef:36]_______. [36: 答案:;]
在长方体ABCD—A1B1C1D1中,|AB|=|AD|=3,
|AA1|=2,点M在A1C1上,|MC1|=2|A1M|,N在
D1C上且为D1C中点,求M、N两点间的距离.[endnoteRef:37]
[37: 答案:;
解 如图分别以AB、AD、AA1所在的直线为x轴、y轴、z轴建立空间直角坐标系.
由题意可知C(3,3,0),
D(0,3,0),∵|DD1|=|CC1|=2,∴C1(3,3,2),D1(0,3,2),∵N为CD1的中点,
∴N.
M是A1C1的三分之一分点且靠近A1点,∴M(1,1,2).
由两点间距离公式,得|MN|==.
]
在空间直角坐标系中,已知点A(1,0,2),B(1,-3,1),
点M在y轴上,且M到A与到B的距离相等,则M的坐标是____[endnoteRef:38]____. [38: 答案:(0,-1,0);
解析 设M的坐标为(0,y,0),由|MA|=|MB|得(0-1)2+(y-0)2+(0-2)2=(0-1)2+(y+3)2+(0-1)2,整理得6y+6=0,
∴y=-1,即点M的坐标为(0,-1,0).
]
空间直角坐标系中,点A(3,2,-5)到x轴的距离d等于( [endnoteRef:39] )
A. B. C. D. [39: 答案:B;
[解析] 过A作AB⊥x轴于B,则B(3,0,0),则点A到x轴的距离d=|AB|=.]
在空间直角坐标系中,点P(3,4,5)关于yOz平面的对称点的坐标为( [endnoteRef:40] )
A.(-3,4,5) B.(-3,-4,5) C.(3,-4,-5) D.(-3,4,-5) [40: 答案:A;
[两点关于平面yOz对称,坐标关系:横坐标相反,纵竖坐标相同.]
]
在空间直角坐标系中,P(2,3,4)、Q(-2,-3,-4)两点的位置关系是( [endnoteRef:41] )
A.关于x轴对称 B.关于yOz平面对称 C.关于坐标原点对称 D.以上都不对 [41: 答案:C;
[三坐标均相反时,两点关于原点对称.]]
正方体ABCD-A1B1C1D1中,点E、F分别是底面A1C1和侧面CD1的中心,若+λ=0(λ∈R),
则λ=____[endnoteRef:42]____. [42: 答案:-;
解析: 如图,连结A1C1,C1D,则E在A1C1上,F在C1D上,
易知EF綊A1D,∴=,即E-=0,∴λ=-.
答案: -
]
