《空间向量》专题3 非坐标运算 学案(Word版含答案)
文档属性
| 名称 | 《空间向量》专题3 非坐标运算 学案(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 267.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-28 07:07:35 | ||
图片预览

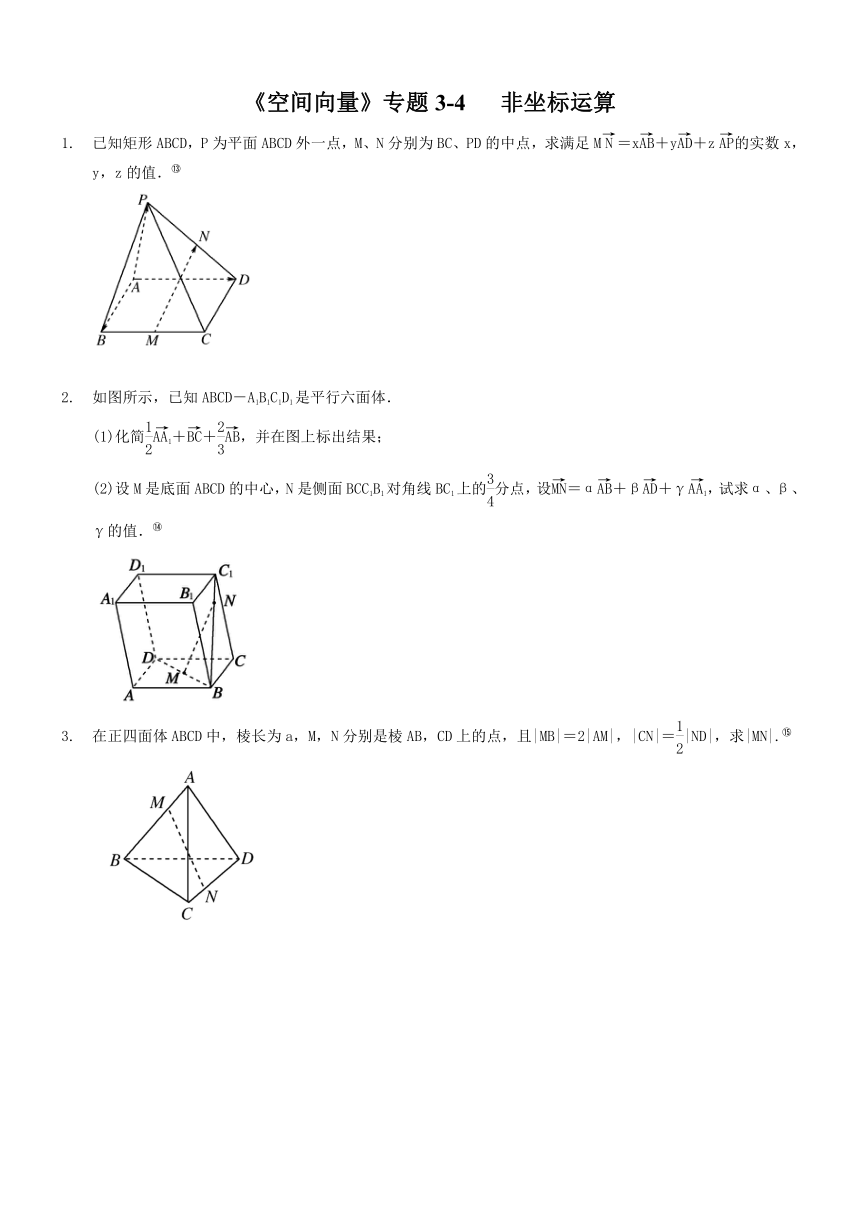
文档简介
《空间向量》专题3-1 非坐标运算
(4套,4页,含答案)
知识点:
非坐标运算: (1)加减与数乘运算: 定义:与平面向量运算一样,空间向量的加法、减法与数乘向量运算如下 ;;; (2)运算律:
⑴加法交换律:;
⑵加法结合律:;
⑶数乘分配律:; 用行路法分解向量,会比较简单,容易理解。
具体操作方法:假设自己行路,绕路行,如果行路方向与向量方向一致,则向量为正,否则为负;把行
路经过的向量相加即为该向量分解的结果。 (4)向量的数量积: . 已知向量和轴,是上与同方向的单位向量,作点在上的射影,作点在上的射影,则叫做向量在轴上或在上的正射影. 可以证明的长度.
(5)空间向量数量积的性质: (1).(2).(3).
(6)空间向量数量积运算律: (1). (2)(交换律)(3)(分配律).
典型例题:
在空间四边形OABC中, +-等于( [endnoteRef:0] )
A. B. C. D. [0: 答案:C;
解析: +-=O-=+=.]
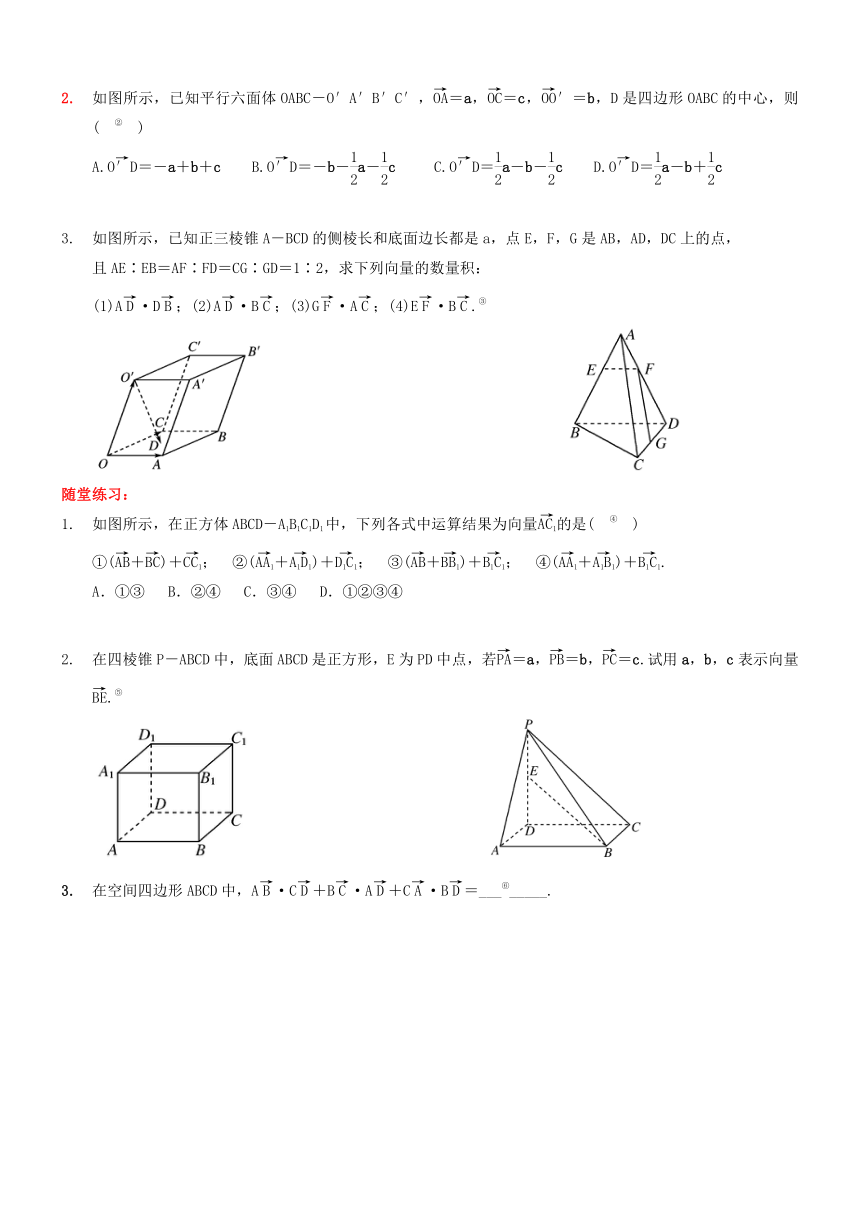
如图所示,已知平行六面体OABC-O′A′B′C′,=a,=c,′=b,D是四边形OABC的中心,则( [endnoteRef:1] )
A.=-a+b+c B.=-b-a-c C.=a-b-c D.=a-b+c
[1: 答案:D;
解析: =+=+=+(+)=a-b+c.]
如图所示,已知正三棱锥A-BCD的侧棱长和底面边长都是a,点E,F,G是AB,AD,DC上的点,
且AE∶EB=AF∶FD=CG∶GD=1∶2,求下列向量的数量积:
(1)A·D;(2)A·B;(3)G·A;(4)E·B.[endnoteRef:2] [2: 答案:-a2,0,-a2,a2;
解析: (1)|A|=a,||=a,〈A,D〉=120°,
所以A·D=|||D|cos 120°=-a2.
(2)因为B=A-A,
所以A·B=A·(A-A)=A·A-A·A,
又因为|A|=a,||=a,〈A,A〉=〈A,A〉=60°,
所以A·B=a2-a2=0.
(3)因为点F,G是AD,DC上的点,
所以G==-A,
所以G·A=-,
因为=a2,
所以G·A=-a2.
(4)因为点E,F分别是AB,AD上的点,所以E=B,
所以E·B=B·B,
结合图形可知〈B,B〉=60°,
所以E·B=B·B=×a×a×cos 60°=a2.
]
随堂练习:
如图所示,在正方体ABCD-A1B1C1D1中,下列各式中运算结果为向量的是( [endnoteRef:3] )
①(+)+; ②(+)+; ③(+)+; ④(+)+.
A.①③ B.②④ C.③④ D.①②③④
[3: 答案:D;
解析: ①(+)+=+=;
②(+)+=+=;
③(+)+=+=;
④(+)+=+=.
]
在四棱锥P-ABCD中,底面ABCD是正方形,E为PD中点,若=a,=b,=c.试用a,b,c表示向量.[endnoteRef:4] [4: 答案:a-b+c;
解析: =(+)=(++)
=(-+--)
=-+
=a-b+c.
]
在空间四边形ABCD中,A·C+B·A+C·B=___[endnoteRef:5]_____. [5: 答案:0;
解析: 设A=b,A=c,A=d,
则C=d-c,B=d-b,=c-b.原式=0.
]
《空间向量》专题3-2 非坐标运算
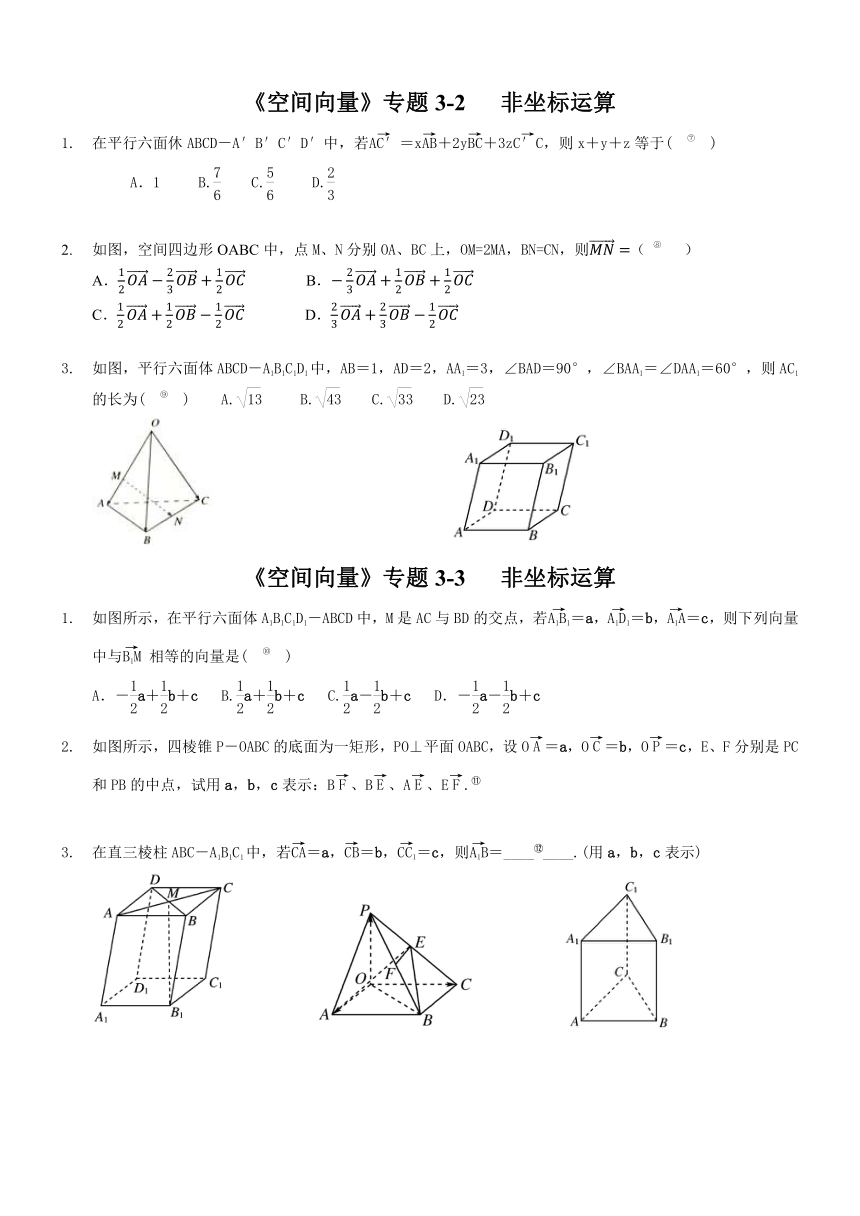
在平行六面休ABCD-A′B′C′D′中,若=x+2y+3z,则x+y+z等于( [endnoteRef:6] )
A.1 B. C. D. [6: 答案:B;
解析: 如图,
=++
=+-,
所以x=1,2y=1,3z=-1,
所以x=1,y=,z=-,
因此x+y+z=1+-=.]
如图,空间四边形OABC中,点M、N分别OA、BC上,OM=2MA,BN=CN,则( [endnoteRef:7] )
A. B.
C. D.
[7: 答案:B;]
如图,平行六面体ABCD-A1B1C1D1中,AB=1,AD=2,AA1=3,∠BAD=90°,∠BAA1=∠DAA1=60°,则AC1的长为( [endnoteRef:8] ) A. B. C. D.
[8: 答案:D;
解析: ∵=A+A+,
∴||==
∵AB=1,AD=2,AA1=3,∠BAD=90°,∠BAA1=∠DAA1=60°,
∴〈A,A〉=90°,〈A,〉=〈A,〉=60°.
∴|A|==.]
《空间向量》专题3-3 非坐标运算
如图所示,在平行六面体A1B1C1D1-ABCD中,M是AC与BD的交点,若=a,=b,=c,则下列向量中与 相等的向量是( [endnoteRef:9] )
A.-a+b+c B.a+b+c C.a-b+c D.-a-b+c [9: 答案:A;
解析: =+=+(+)=c+(-a+b)=-a+b+c.]
如图所示,四棱锥P-OABC的底面为一矩形,PO⊥平面OABC,设O=a,O=b,O=c,E、F分别是PC和PB的中点,试用a,b,c表示:B、B、A、E.[endnoteRef:10]
[10: 答案:B=-a-b+c,B=-a-b+c,A=-a+b+c,E=a;
解析: 连结BO,则B=B=(B+O)=(c-b-a)=-a-b+c.
B=B+C=-a+C=-a+(C+O)=-a-b+c.
A=A+P=A+O+(P+O)=-a+c+(-c+b)=-a+b+c.
E=C=O=a.
]
在直三棱柱ABC-A1B1C1中,若=a,=b,=c,则=____[endnoteRef:11]____.(用a,b,c表示)
[11: 答案:-a+b-c;
解析: =-=-(+)=-a+b-c.]
《空间向量》专题3-4 非坐标运算
已知矩形ABCD,P为平面ABCD外一点,M、N分别为BC、PD的中点,求满足M=x+y+z的实数x,y,z的值.[endnoteRef:12]
[12: 答案:x=-1,y=0,z=;
解析: =++=++=-+(-)=-+,
∴x=-1,y=0,z=.
]
如图所示,已知ABCD-A1B1C1D1是平行六面体.
(1)化简++,并在图上标出结果;
(2)设M是底面ABCD的中心,N是侧面BCC1B1对角线BC1上的分点,设=α+β+γ,试求α、β、γ的值.[endnoteRef:13]
[13: 答案:作图略,α=,β=,γ=;
解析:
(1)如图所示,取AA1的中点E,在D1C1上取一点F,使得D1F=2FC1,则=++.
(2)=+=+=(+)+(+)=++.
∴α=,β=,γ=.
]
在正四面体ABCD中,棱长为a,M,N分别是棱AB,CD上的点,且|MB|=2|AM|,|CN|=|ND|,求|MN|.[endnoteRef:14]
[14: 答案:a;
解析: ∵M=M+B+C=A+(A-A)+(A-A)=-A+A+A.
∴M·M=(-A+A+)·(-A+A+A)
=-A·A-A·A+A·A+2+
=a2-a2-a2+a2+a2+a2=a2.
故|M|==a.
即|MN|=a.
]
(4套,4页,含答案)
知识点:
非坐标运算: (1)加减与数乘运算: 定义:与平面向量运算一样,空间向量的加法、减法与数乘向量运算如下 ;;; (2)运算律:
⑴加法交换律:;
⑵加法结合律:;
⑶数乘分配律:; 用行路法分解向量,会比较简单,容易理解。
具体操作方法:假设自己行路,绕路行,如果行路方向与向量方向一致,则向量为正,否则为负;把行
路经过的向量相加即为该向量分解的结果。 (4)向量的数量积: . 已知向量和轴,是上与同方向的单位向量,作点在上的射影,作点在上的射影,则叫做向量在轴上或在上的正射影. 可以证明的长度.
(5)空间向量数量积的性质: (1).(2).(3).
(6)空间向量数量积运算律: (1). (2)(交换律)(3)(分配律).
典型例题:
在空间四边形OABC中, +-等于( [endnoteRef:0] )
A. B. C. D. [0: 答案:C;
解析: +-=O-=+=.]
如图所示,已知平行六面体OABC-O′A′B′C′,=a,=c,′=b,D是四边形OABC的中心,则( [endnoteRef:1] )
A.=-a+b+c B.=-b-a-c C.=a-b-c D.=a-b+c
[1: 答案:D;
解析: =+=+=+(+)=a-b+c.]
如图所示,已知正三棱锥A-BCD的侧棱长和底面边长都是a,点E,F,G是AB,AD,DC上的点,
且AE∶EB=AF∶FD=CG∶GD=1∶2,求下列向量的数量积:
(1)A·D;(2)A·B;(3)G·A;(4)E·B.[endnoteRef:2] [2: 答案:-a2,0,-a2,a2;
解析: (1)|A|=a,||=a,〈A,D〉=120°,
所以A·D=|||D|cos 120°=-a2.
(2)因为B=A-A,
所以A·B=A·(A-A)=A·A-A·A,
又因为|A|=a,||=a,〈A,A〉=〈A,A〉=60°,
所以A·B=a2-a2=0.
(3)因为点F,G是AD,DC上的点,
所以G==-A,
所以G·A=-,
因为=a2,
所以G·A=-a2.
(4)因为点E,F分别是AB,AD上的点,所以E=B,
所以E·B=B·B,
结合图形可知〈B,B〉=60°,
所以E·B=B·B=×a×a×cos 60°=a2.
]
随堂练习:
如图所示,在正方体ABCD-A1B1C1D1中,下列各式中运算结果为向量的是( [endnoteRef:3] )
①(+)+; ②(+)+; ③(+)+; ④(+)+.
A.①③ B.②④ C.③④ D.①②③④
[3: 答案:D;
解析: ①(+)+=+=;
②(+)+=+=;
③(+)+=+=;
④(+)+=+=.
]
在四棱锥P-ABCD中,底面ABCD是正方形,E为PD中点,若=a,=b,=c.试用a,b,c表示向量.[endnoteRef:4] [4: 答案:a-b+c;
解析: =(+)=(++)
=(-+--)
=-+
=a-b+c.
]
在空间四边形ABCD中,A·C+B·A+C·B=___[endnoteRef:5]_____. [5: 答案:0;
解析: 设A=b,A=c,A=d,
则C=d-c,B=d-b,=c-b.原式=0.
]
《空间向量》专题3-2 非坐标运算
在平行六面休ABCD-A′B′C′D′中,若=x+2y+3z,则x+y+z等于( [endnoteRef:6] )
A.1 B. C. D. [6: 答案:B;
解析: 如图,
=++
=+-,
所以x=1,2y=1,3z=-1,
所以x=1,y=,z=-,
因此x+y+z=1+-=.]
如图,空间四边形OABC中,点M、N分别OA、BC上,OM=2MA,BN=CN,则( [endnoteRef:7] )
A. B.
C. D.
[7: 答案:B;]
如图,平行六面体ABCD-A1B1C1D1中,AB=1,AD=2,AA1=3,∠BAD=90°,∠BAA1=∠DAA1=60°,则AC1的长为( [endnoteRef:8] ) A. B. C. D.
[8: 答案:D;
解析: ∵=A+A+,
∴||==
∵AB=1,AD=2,AA1=3,∠BAD=90°,∠BAA1=∠DAA1=60°,
∴〈A,A〉=90°,〈A,〉=〈A,〉=60°.
∴|A|==.]
《空间向量》专题3-3 非坐标运算
如图所示,在平行六面体A1B1C1D1-ABCD中,M是AC与BD的交点,若=a,=b,=c,则下列向量中与 相等的向量是( [endnoteRef:9] )
A.-a+b+c B.a+b+c C.a-b+c D.-a-b+c [9: 答案:A;
解析: =+=+(+)=c+(-a+b)=-a+b+c.]
如图所示,四棱锥P-OABC的底面为一矩形,PO⊥平面OABC,设O=a,O=b,O=c,E、F分别是PC和PB的中点,试用a,b,c表示:B、B、A、E.[endnoteRef:10]
[10: 答案:B=-a-b+c,B=-a-b+c,A=-a+b+c,E=a;
解析: 连结BO,则B=B=(B+O)=(c-b-a)=-a-b+c.
B=B+C=-a+C=-a+(C+O)=-a-b+c.
A=A+P=A+O+(P+O)=-a+c+(-c+b)=-a+b+c.
E=C=O=a.
]
在直三棱柱ABC-A1B1C1中,若=a,=b,=c,则=____[endnoteRef:11]____.(用a,b,c表示)
[11: 答案:-a+b-c;
解析: =-=-(+)=-a+b-c.]
《空间向量》专题3-4 非坐标运算
已知矩形ABCD,P为平面ABCD外一点,M、N分别为BC、PD的中点,求满足M=x+y+z的实数x,y,z的值.[endnoteRef:12]
[12: 答案:x=-1,y=0,z=;
解析: =++=++=-+(-)=-+,
∴x=-1,y=0,z=.
]
如图所示,已知ABCD-A1B1C1D1是平行六面体.
(1)化简++,并在图上标出结果;
(2)设M是底面ABCD的中心,N是侧面BCC1B1对角线BC1上的分点,设=α+β+γ,试求α、β、γ的值.[endnoteRef:13]
[13: 答案:作图略,α=,β=,γ=;
解析:
(1)如图所示,取AA1的中点E,在D1C1上取一点F,使得D1F=2FC1,则=++.
(2)=+=+=(+)+(+)=++.
∴α=,β=,γ=.
]
在正四面体ABCD中,棱长为a,M,N分别是棱AB,CD上的点,且|MB|=2|AM|,|CN|=|ND|,求|MN|.[endnoteRef:14]
[14: 答案:a;
解析: ∵M=M+B+C=A+(A-A)+(A-A)=-A+A+A.
∴M·M=(-A+A+)·(-A+A+A)
=-A·A-A·A+A·A+2+
=a2-a2-a2+a2+a2+a2=a2.
故|M|==a.
即|MN|=a.
]
