人教版九年级上册数学23.2.3关于原点对称的点的坐标 教学设计
文档属性
| 名称 | 人教版九年级上册数学23.2.3关于原点对称的点的坐标 教学设计 |

|
|
| 格式 | doc | ||
| 文件大小 | 145.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-28 00:00:00 | ||
图片预览

文档简介
23.2.3关于原点对称的点的坐标
一、学习目标
1.理解并掌握关于原点对称的点的坐标特征,会运用关于原点对称的点的坐标特征解决相关问题;
2.运用轴对称、旋转、中心对称的知识探究关于原点对称的点的坐标的特征;
3.在探究过程中体会类比思想和数形结合思想在数学中的作用。
二、重点和难点
重点:掌握点P(x,y)关于原点的对称点P’(-x,-y)及其应用.
难点:运用中心对称的知识推导出点P(x,y)关于原点对称的点P’(-x,-y).
学习过程
(一)问题导入:
1、下列各点分别在坐标平面的什么位置上?
A(3,2)————
B(0,-2)————
C(-3,-2)————
D(-3,0)————
E(-1.5,3.5)————
F(2,-3)————
2、在平面直角坐标系中,关于X轴、y轴对称的点的坐标具有怎样的关系
(二)自主学习:
自学指导:研读教材P68的内容,要求:
1、思考关于原点对称的两点在直角坐标中位置的特点。
2、认真研究例2,掌握作出与△ABC关于原点对称的图形的作图方法。
(三)自学检测
(1)在平面直角坐标系中,两个点关于原点对称时,它们的坐标 ,
即点P(x,y)关于原点对称的点的坐标P’( , )。
(2)点A(2,-3)关于原点对称的点的坐标A’( , );
点B(0,7)关于原点对称的点的坐标B’( , );
点C(-8,-1)关于原点对称的点的坐标C’( , )。
(四)探究新知
探究1:关于原点对称的点的坐标
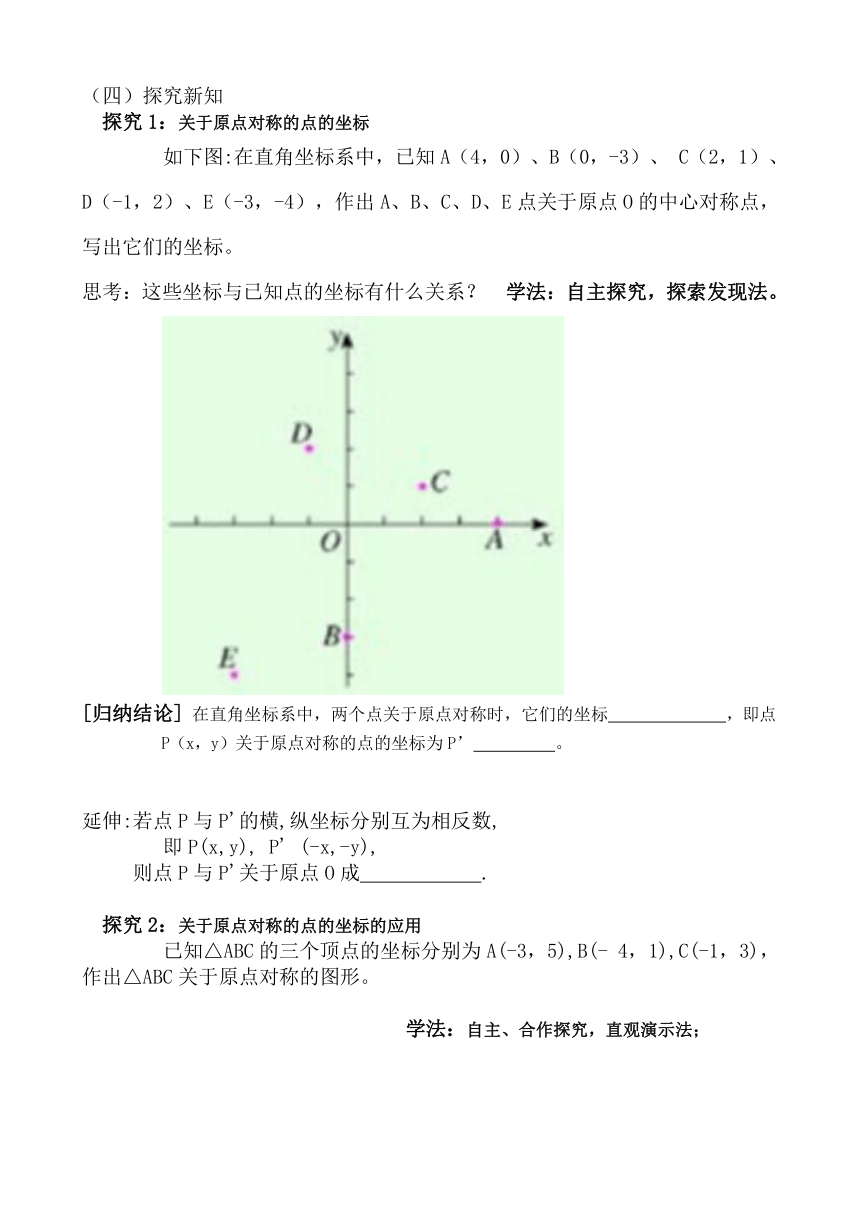
如下图:在直角坐标系中,已知A(4,0)、B(0,-3)、 C(2,1)、D(-1,2)、E(-3,-4),作出A、B、C、D、E点关于原点O的中心对称点,写出它们的坐标。
思考:这些坐标与已知点的坐标有什么关系? 学法:自主探究,探索发现法。
[归纳结论] 在直角坐标系中,两个点关于原点对称时,它们的坐标 ,即点P(x,y)关于原点对称的点的坐标为P’ 。
延伸:若点P与P'的横,纵坐标分别互为相反数,
即P(x,y), P' (-x,-y),
则点P与P'关于原点O成 .
探究2:关于原点对称的点的坐标的应用
已知△ABC的三个顶点的坐标分别为A(-3,5),B(- 4,1),C(-1,3),作出△ABC关于原点对称的图形。
学法:自主、合作探究,直观演示法;
思考:在平面直角坐标系中,作关于原点的中心对称的图形的步骤
作图步骤:、写出各点关于原点对称的点的坐标。
、在坐标平面内描出这些对称点的位置。
、顺次连接各点即为所求做的对称图形。
(五)当堂检测
1、下列各点中哪两个点关于原点对称?
A(-5,0)、 B(0,2)、 C(2,-1)、 D(2,0)、 E(0,5)、
F(-2,1)、 G(-2,-1)。
2、已知点A(a,1) 和点A’(5,b)是关于原点O的对称点,求a+b= 。
3、若点P(-1-2a,2a-4)关于原点对称的点是第一象限的点,则a整
数解有( )
A.1个 B.2个 C.3个 D.4个
4、四边形ABCD各顶点的坐标分别为A(5,0),B(-2,3),C(-1,0), D(-1,-5),作出与四边形ABCD关于原点O对称的图形。
(六)收获与评价
1、会求已知点关于原点对称的点的坐标。
2、会利用坐标画出关于原点对称的图形。
(七)作业布置:课本P70 第3、4题;
(八)板书设计
23.2.3关于原点对称的点的坐标
在直角坐标系中,两个点关于原点对称时,它们的坐标符号相反,即
点P(x,y)关于原点对称的点的坐标为P’(-x,-y)。
作图步骤:、写出各点关于原点对称的点的坐标。
、在坐标平面内描出这些对称点的位置。
、顺次连接各点即为所求做的对称图形。
3
一、学习目标
1.理解并掌握关于原点对称的点的坐标特征,会运用关于原点对称的点的坐标特征解决相关问题;
2.运用轴对称、旋转、中心对称的知识探究关于原点对称的点的坐标的特征;
3.在探究过程中体会类比思想和数形结合思想在数学中的作用。
二、重点和难点
重点:掌握点P(x,y)关于原点的对称点P’(-x,-y)及其应用.
难点:运用中心对称的知识推导出点P(x,y)关于原点对称的点P’(-x,-y).
学习过程
(一)问题导入:
1、下列各点分别在坐标平面的什么位置上?
A(3,2)————
B(0,-2)————
C(-3,-2)————
D(-3,0)————
E(-1.5,3.5)————
F(2,-3)————
2、在平面直角坐标系中,关于X轴、y轴对称的点的坐标具有怎样的关系
(二)自主学习:
自学指导:研读教材P68的内容,要求:
1、思考关于原点对称的两点在直角坐标中位置的特点。
2、认真研究例2,掌握作出与△ABC关于原点对称的图形的作图方法。
(三)自学检测
(1)在平面直角坐标系中,两个点关于原点对称时,它们的坐标 ,
即点P(x,y)关于原点对称的点的坐标P’( , )。
(2)点A(2,-3)关于原点对称的点的坐标A’( , );
点B(0,7)关于原点对称的点的坐标B’( , );
点C(-8,-1)关于原点对称的点的坐标C’( , )。
(四)探究新知
探究1:关于原点对称的点的坐标
如下图:在直角坐标系中,已知A(4,0)、B(0,-3)、 C(2,1)、D(-1,2)、E(-3,-4),作出A、B、C、D、E点关于原点O的中心对称点,写出它们的坐标。
思考:这些坐标与已知点的坐标有什么关系? 学法:自主探究,探索发现法。
[归纳结论] 在直角坐标系中,两个点关于原点对称时,它们的坐标 ,即点P(x,y)关于原点对称的点的坐标为P’ 。
延伸:若点P与P'的横,纵坐标分别互为相反数,
即P(x,y), P' (-x,-y),
则点P与P'关于原点O成 .
探究2:关于原点对称的点的坐标的应用
已知△ABC的三个顶点的坐标分别为A(-3,5),B(- 4,1),C(-1,3),作出△ABC关于原点对称的图形。
学法:自主、合作探究,直观演示法;
思考:在平面直角坐标系中,作关于原点的中心对称的图形的步骤
作图步骤:、写出各点关于原点对称的点的坐标。
、在坐标平面内描出这些对称点的位置。
、顺次连接各点即为所求做的对称图形。
(五)当堂检测
1、下列各点中哪两个点关于原点对称?
A(-5,0)、 B(0,2)、 C(2,-1)、 D(2,0)、 E(0,5)、
F(-2,1)、 G(-2,-1)。
2、已知点A(a,1) 和点A’(5,b)是关于原点O的对称点,求a+b= 。
3、若点P(-1-2a,2a-4)关于原点对称的点是第一象限的点,则a整
数解有( )
A.1个 B.2个 C.3个 D.4个
4、四边形ABCD各顶点的坐标分别为A(5,0),B(-2,3),C(-1,0), D(-1,-5),作出与四边形ABCD关于原点O对称的图形。
(六)收获与评价
1、会求已知点关于原点对称的点的坐标。
2、会利用坐标画出关于原点对称的图形。
(七)作业布置:课本P70 第3、4题;
(八)板书设计
23.2.3关于原点对称的点的坐标
在直角坐标系中,两个点关于原点对称时,它们的坐标符号相反,即
点P(x,y)关于原点对称的点的坐标为P’(-x,-y)。
作图步骤:、写出各点关于原点对称的点的坐标。
、在坐标平面内描出这些对称点的位置。
、顺次连接各点即为所求做的对称图形。
3
同课章节目录
