第六讲 解三角形 学案(Word版无答案)
文档属性
| 名称 | 第六讲 解三角形 学案(Word版无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 637.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-28 15:08:53 | ||
图片预览




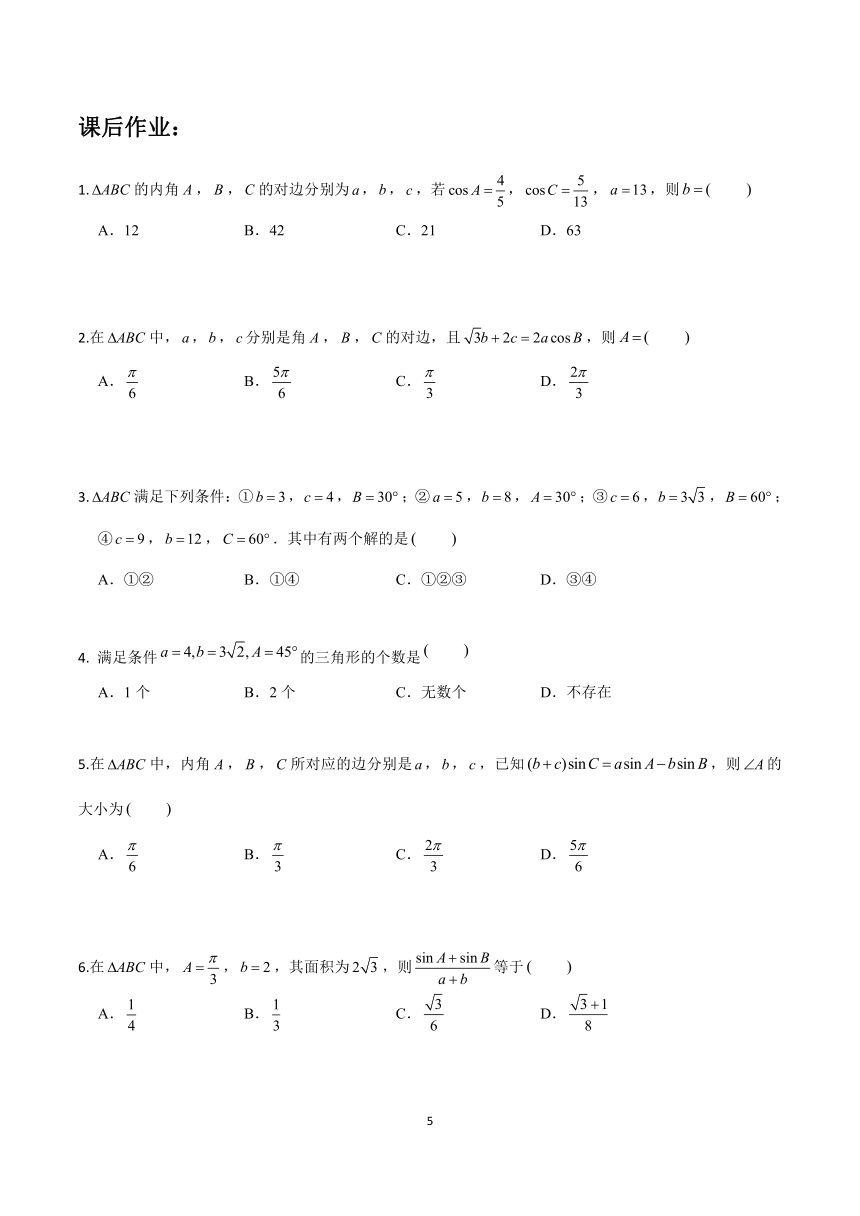
文档简介
第六讲 解三角形
模块一:正余弦定理
一、在中的三个内角,,的对边,分别用,,表示.
正弦定理:
2.余弦定理:
二、解决三角形的综合问题时,要注意以下关系式的运用
① .
② ;.
③ ;.
④ .
考点1:已知三角形的任意两个角与一边
(1)在中,,,c=2,求,b,C
(2)在中,角,,所对应的边分别为,,.若,,,则
A.1 B. C.2 D.
考点2:已知三角形的两边与其中一边的对角
(1)中,a=2,b=6,A=30,求B、C、c
考点3:已知两边及其夹角
(1)中,a=2,c=+,B=45,求b、A
考点4:已知三角形的三边
中,a=7 、b=3 、c=5,求最大角和sinC
考点5:正余弦定理综合
(1)中,角,,的对边分别为,,,若,.且,则的面积为
A.2 B.3 C.4 D.
(2)在中,内角,,所对应的边分别是,,,已知,则的大小为
A. B. C. D.
例6.(1)在中,角,,对边分别为,,.已知,,则角
A. B. C. D.
(2)在中,,,分别是角,,的对边,且,则
A. B. C. D.
模块二:判断三角形解的个数
分类:
当A为锐角时,
当A为钝角或直角时,
【例1】下列三角形是否有解?有解的作出解答.
(1)a=7,b=8,A=105°;
(2)b=10,c=5,C=60°;
(3)a=2,b=6,A=30°.
(1)在三角形中,根据下列条件解三角形,其中有两个解的是 。
A.,, B.,,
C.,, D.,,
(2)(莲都区校级月考)在中,若,,,那么满足条件的
A.有一个 B.有两个 C.不存在 D.不能确定
(3)(上高县校级月考)满足下列条件:①,,;②,,;③,,;④,,.其中有两个解的是
A.①② B.①④ C.①②③ D.③④
模块三:判断三角形形状
1.与三角形形状相关的几个结论
① 在中,若,则为等腰三角形或直角三角形;
② 在中,若,则为等边三角形;
③ 在中,若,则为直角三角形;
④ 在中,若,则为直角三角形;
⑤ 在中,若,则为直角三角形.
在中,直线b x+ y cosA+ cosB=0与a x+ y cosB+ cosA=0平行,则一定是( )
A.等腰三角形 B.直角三角形
C.锐角三角形 D.等腰或直角三角形
(1)(上高县校级月考)在中,内角,,的对边分别为,,,若,,则一定是
A.等腰三角形非直角三角形 B.直角三角形非等腰三角形
C.等边三角形 D.等腰直角三角形
(2)在中,,则这三角形一定是( )
A.等腰三角形 B.直角三角形
C.等腰直角三角形 D.等腰或直角三角形
(3)在中,,则这三角形一定是( )
A.等腰三角形 B.直角三角形
C.等腰直角三角形 D.等腰或直角三角形
课后作业:
1.的内角,,的对边分别为,,,若,,,则
A.12 B.42 C.21 D.63
2.在中,,,分别是角,,的对边,且,则
A. B. C. D.
3.满足下列条件:①,,;②,,;③,,;④,,.其中有两个解的是
A.①② B.①④ C.①②③ D.③④
满足条件的三角形的个数是
A.1个 B.2个 C.无数个 D.不存在
5.在中,内角,,所对应的边分别是,,,已知,则的大小为
A. B. C. D.
6.在中,,,其面积为,则等于
A. B. C. D.
模块四:实际问题
考点1:求高度
例1、如图所示,为测一建筑物的高度,在地面上选取A,B两点,从A,B两点测得建筑物顶端的仰角分别为30°,45°,且A,B两点间的距离为60 m,则该建筑物的高度为( )
例2、如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶600m后到达B处,测得此山顶在西偏北75°的方向上,仰角为30°,则此山的高度CD=( )m.
在一座高的观测台台顶测得对面一水塔塔顶仰角为, 塔底俯角为, 那么这座塔的高为
A. B. C. D.
考点2:求距离
例2、如图所示,A,B是海平面上的两个小岛,为测量A,B两岛间的距离,测量船以15海里/时的速度
沿既定直线CD航行,在t时刻航行到C处,测得∠ACB=75°,∠ACD=120°,1小时后,测量船到达D
处,测得∠ADC=30°,∠ADB=45°,求A,B两小岛间的距离.(注:A、B、C、D四点共面)
如图,,是海面上位于东西方向相距海里的两个观测点,现位于点北偏东,点北偏西的点有一艘轮船发出求救信号,位于点南偏西且与点相距海里的点的救援船立即前往营救,其航行速度为30海里/小时,该救援船达到点需要多长时间?
考点3:角度问题
例3 甲船在A点发现乙船在北偏东60°的B处,乙船以每小时a海里的速度向北行驶,已知甲船的速度是每小时a海里,问甲船应沿着什么方向前进,才能最快与乙船相遇?
(1) 当太阳光与水平面的倾斜角为60°时,一根长为2 m的竹竿如图所示放置,要使它的影子最长,则竹竿与地面所成的角是( )
A.15° B.30° C.45° D.60°
1如图所示,D,C,B在地平面同一直线上,DC=10 m,从D,C两地测得A点的仰角分别为30°和45°,则A点离地面的高AB等于( )
A.10 m B.5 m
C.5(-1) m D.5(+1) m
2.已知海上A,B两个小岛相距10海里,C岛临近陆地,若从A岛望C岛和B岛成60°的视角,从B岛望C岛和A岛成75°视角,则B岛与C岛之间的距离是( )
A.10 海里 B. 海里
C.5 海里 D.5 海里
3.如图,两座相距60 m的建筑物AB,CD的高度分别为20 m,50 m,BD为水平面,则从建筑物AB的顶端A看建筑物CD的张角为( )
A.30° B.45° C.60° D.75°
4.如图所示,位于A处的信息中心获悉:在其正东方向相距40海里的B处有一艘渔船遇险,在原地等待营救.信息中心立即把消息告知在其南偏西30°、相距20海里的C处的乙船,现乙船朝北偏东θ的方向沿直线CB前往B处救援,则cos θ的值为 .
5.如图,在海岸A处发现北偏东45°方向,距A处(-1)海里的B处有一艘走私船.在A处北偏西75°方向,距A处2海里的C处的我方缉私船奉命以10 海里/时的速度追截走私船,此时走私船正以10海里/时的速度,从B处向北偏东30°方向逃窜.问:缉私船沿什么方向行驶才能最快截获走私船?并求出所需时间.
考点4:正余弦定理综合应用
例4.(1)在中,角,,的对边分别为,,,,的外接圆半径为,则的值为
A.1 B.2 C. D.
(2)在中,已知三个内角为,,满足,则
A. B. C. D.
(3)已知的面积为,角,,的对边分别为,,,若,,则
A.16 B.12 C.8 D.4
(4)(梅河口市校级月考)在中,,,其面积为,则等于
A. B. C. D.
课后作业
1.如图所示,设A,B两点在河的两岸,一测量者与A在河的同侧,在所在的河岸边先确定一点C,测出A,C的距离为50 m,∠ACB=45°,∠CAB=105°后,可以计算出A,B两点的距离为( )
A.50 m B.50 m
C.25 m D. m
2.如图,要测出山上一座天文台BC的高,从山腰A处测得AC=60 m,天文台最高处B的仰角为45°,天文台底部C的仰角为15°,则天文台BC的高为( )
A.20 m B.30 m
C.20 m D.30 m
3.如图所示,在坡度一定的山坡A处测得山顶上一建筑物CD的顶端C对于山坡的斜度为15°,向山顶前进100 m到达B处,又测得C对于山坡的斜度为45°,若CD=50 m,山坡对于地平面的坡度为θ,则cos θ等于( )
A. B. C.-1 D.-1
4.两座灯塔A,B与海洋观测站C的距离分别为a n mile,2a n mile,灯塔A在观测站的北偏东35°的方向上,灯塔B在观测站的南偏东25°的方向上,则灯塔A与灯塔B的距离为( )
A.3a n mile B.a n mile
C.a n mile D.a n mile
5.如图,已知两座灯塔A,B与海洋观察站C的距离相等,灯塔A在观察站C的北偏东40°,灯塔B在观察站C的南偏东60°,则灯塔A在灯塔B的( )
A.北偏东10° B.北偏西10°
C.南偏东10° D.南偏西10°
6.一艘船以每小时15 km的速度向东航行,船在A处看到一个灯塔B在北偏东60°,行驶4 h后,船到达C处,看到这个灯塔在北偏东15°,这时船与灯塔间的距离为 km.
7.如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距6 n mile,渔船乙以5 n mile/h的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙,刚好用2 h追上.
(1)求渔船甲的速度;
(2)求sin α.
8.如图,游客从某旅游景区的景点A处下山至C处有两种路径:一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.山路AC长为1 260 m,经测量,cos A=,cos C=.求索道AB的长.
2
模块一:正余弦定理
一、在中的三个内角,,的对边,分别用,,表示.
正弦定理:
2.余弦定理:
二、解决三角形的综合问题时,要注意以下关系式的运用
① .
② ;.
③ ;.
④ .
考点1:已知三角形的任意两个角与一边
(1)在中,,,c=2,求,b,C
(2)在中,角,,所对应的边分别为,,.若,,,则
A.1 B. C.2 D.
考点2:已知三角形的两边与其中一边的对角
(1)中,a=2,b=6,A=30,求B、C、c
考点3:已知两边及其夹角
(1)中,a=2,c=+,B=45,求b、A
考点4:已知三角形的三边
中,a=7 、b=3 、c=5,求最大角和sinC
考点5:正余弦定理综合
(1)中,角,,的对边分别为,,,若,.且,则的面积为
A.2 B.3 C.4 D.
(2)在中,内角,,所对应的边分别是,,,已知,则的大小为
A. B. C. D.
例6.(1)在中,角,,对边分别为,,.已知,,则角
A. B. C. D.
(2)在中,,,分别是角,,的对边,且,则
A. B. C. D.
模块二:判断三角形解的个数
分类:
当A为锐角时,
当A为钝角或直角时,
【例1】下列三角形是否有解?有解的作出解答.
(1)a=7,b=8,A=105°;
(2)b=10,c=5,C=60°;
(3)a=2,b=6,A=30°.
(1)在三角形中,根据下列条件解三角形,其中有两个解的是 。
A.,, B.,,
C.,, D.,,
(2)(莲都区校级月考)在中,若,,,那么满足条件的
A.有一个 B.有两个 C.不存在 D.不能确定
(3)(上高县校级月考)满足下列条件:①,,;②,,;③,,;④,,.其中有两个解的是
A.①② B.①④ C.①②③ D.③④
模块三:判断三角形形状
1.与三角形形状相关的几个结论
① 在中,若,则为等腰三角形或直角三角形;
② 在中,若,则为等边三角形;
③ 在中,若,则为直角三角形;
④ 在中,若,则为直角三角形;
⑤ 在中,若,则为直角三角形.
在中,直线b x+ y cosA+ cosB=0与a x+ y cosB+ cosA=0平行,则一定是( )
A.等腰三角形 B.直角三角形
C.锐角三角形 D.等腰或直角三角形
(1)(上高县校级月考)在中,内角,,的对边分别为,,,若,,则一定是
A.等腰三角形非直角三角形 B.直角三角形非等腰三角形
C.等边三角形 D.等腰直角三角形
(2)在中,,则这三角形一定是( )
A.等腰三角形 B.直角三角形
C.等腰直角三角形 D.等腰或直角三角形
(3)在中,,则这三角形一定是( )
A.等腰三角形 B.直角三角形
C.等腰直角三角形 D.等腰或直角三角形
课后作业:
1.的内角,,的对边分别为,,,若,,,则
A.12 B.42 C.21 D.63
2.在中,,,分别是角,,的对边,且,则
A. B. C. D.
3.满足下列条件:①,,;②,,;③,,;④,,.其中有两个解的是
A.①② B.①④ C.①②③ D.③④
满足条件的三角形的个数是
A.1个 B.2个 C.无数个 D.不存在
5.在中,内角,,所对应的边分别是,,,已知,则的大小为
A. B. C. D.
6.在中,,,其面积为,则等于
A. B. C. D.
模块四:实际问题
考点1:求高度
例1、如图所示,为测一建筑物的高度,在地面上选取A,B两点,从A,B两点测得建筑物顶端的仰角分别为30°,45°,且A,B两点间的距离为60 m,则该建筑物的高度为( )
例2、如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶600m后到达B处,测得此山顶在西偏北75°的方向上,仰角为30°,则此山的高度CD=( )m.
在一座高的观测台台顶测得对面一水塔塔顶仰角为, 塔底俯角为, 那么这座塔的高为
A. B. C. D.
考点2:求距离
例2、如图所示,A,B是海平面上的两个小岛,为测量A,B两岛间的距离,测量船以15海里/时的速度
沿既定直线CD航行,在t时刻航行到C处,测得∠ACB=75°,∠ACD=120°,1小时后,测量船到达D
处,测得∠ADC=30°,∠ADB=45°,求A,B两小岛间的距离.(注:A、B、C、D四点共面)
如图,,是海面上位于东西方向相距海里的两个观测点,现位于点北偏东,点北偏西的点有一艘轮船发出求救信号,位于点南偏西且与点相距海里的点的救援船立即前往营救,其航行速度为30海里/小时,该救援船达到点需要多长时间?
考点3:角度问题
例3 甲船在A点发现乙船在北偏东60°的B处,乙船以每小时a海里的速度向北行驶,已知甲船的速度是每小时a海里,问甲船应沿着什么方向前进,才能最快与乙船相遇?
(1) 当太阳光与水平面的倾斜角为60°时,一根长为2 m的竹竿如图所示放置,要使它的影子最长,则竹竿与地面所成的角是( )
A.15° B.30° C.45° D.60°
1如图所示,D,C,B在地平面同一直线上,DC=10 m,从D,C两地测得A点的仰角分别为30°和45°,则A点离地面的高AB等于( )
A.10 m B.5 m
C.5(-1) m D.5(+1) m
2.已知海上A,B两个小岛相距10海里,C岛临近陆地,若从A岛望C岛和B岛成60°的视角,从B岛望C岛和A岛成75°视角,则B岛与C岛之间的距离是( )
A.10 海里 B. 海里
C.5 海里 D.5 海里
3.如图,两座相距60 m的建筑物AB,CD的高度分别为20 m,50 m,BD为水平面,则从建筑物AB的顶端A看建筑物CD的张角为( )
A.30° B.45° C.60° D.75°
4.如图所示,位于A处的信息中心获悉:在其正东方向相距40海里的B处有一艘渔船遇险,在原地等待营救.信息中心立即把消息告知在其南偏西30°、相距20海里的C处的乙船,现乙船朝北偏东θ的方向沿直线CB前往B处救援,则cos θ的值为 .
5.如图,在海岸A处发现北偏东45°方向,距A处(-1)海里的B处有一艘走私船.在A处北偏西75°方向,距A处2海里的C处的我方缉私船奉命以10 海里/时的速度追截走私船,此时走私船正以10海里/时的速度,从B处向北偏东30°方向逃窜.问:缉私船沿什么方向行驶才能最快截获走私船?并求出所需时间.
考点4:正余弦定理综合应用
例4.(1)在中,角,,的对边分别为,,,,的外接圆半径为,则的值为
A.1 B.2 C. D.
(2)在中,已知三个内角为,,满足,则
A. B. C. D.
(3)已知的面积为,角,,的对边分别为,,,若,,则
A.16 B.12 C.8 D.4
(4)(梅河口市校级月考)在中,,,其面积为,则等于
A. B. C. D.
课后作业
1.如图所示,设A,B两点在河的两岸,一测量者与A在河的同侧,在所在的河岸边先确定一点C,测出A,C的距离为50 m,∠ACB=45°,∠CAB=105°后,可以计算出A,B两点的距离为( )
A.50 m B.50 m
C.25 m D. m
2.如图,要测出山上一座天文台BC的高,从山腰A处测得AC=60 m,天文台最高处B的仰角为45°,天文台底部C的仰角为15°,则天文台BC的高为( )
A.20 m B.30 m
C.20 m D.30 m
3.如图所示,在坡度一定的山坡A处测得山顶上一建筑物CD的顶端C对于山坡的斜度为15°,向山顶前进100 m到达B处,又测得C对于山坡的斜度为45°,若CD=50 m,山坡对于地平面的坡度为θ,则cos θ等于( )
A. B. C.-1 D.-1
4.两座灯塔A,B与海洋观测站C的距离分别为a n mile,2a n mile,灯塔A在观测站的北偏东35°的方向上,灯塔B在观测站的南偏东25°的方向上,则灯塔A与灯塔B的距离为( )
A.3a n mile B.a n mile
C.a n mile D.a n mile
5.如图,已知两座灯塔A,B与海洋观察站C的距离相等,灯塔A在观察站C的北偏东40°,灯塔B在观察站C的南偏东60°,则灯塔A在灯塔B的( )
A.北偏东10° B.北偏西10°
C.南偏东10° D.南偏西10°
6.一艘船以每小时15 km的速度向东航行,船在A处看到一个灯塔B在北偏东60°,行驶4 h后,船到达C处,看到这个灯塔在北偏东15°,这时船与灯塔间的距离为 km.
7.如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距6 n mile,渔船乙以5 n mile/h的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙,刚好用2 h追上.
(1)求渔船甲的速度;
(2)求sin α.
8.如图,游客从某旅游景区的景点A处下山至C处有两种路径:一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.山路AC长为1 260 m,经测量,cos A=,cos C=.求索道AB的长.
2
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
