人教A版(2019)必修第二册8.2立体图形的直观图 同步练习(Word版含解析)
文档属性
| 名称 | 人教A版(2019)必修第二册8.2立体图形的直观图 同步练习(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 783.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-28 15:49:09 | ||
图片预览

文档简介
人教A版(2019)必修第二册 8.2 立体图形的直观图
一、单选题
1.埃及金字塔是古埃及的帝王(法老)陵墓,世界七大奇迹之一,其中较为著名的是胡夫金字塔.令人吃惊的并不仅仅是胡夫金字塔的雄壮身姿,还有发生在胡夫金字塔上的数字“巧合”.如胡夫金字塔的底部周长如果除以其高度的两倍,得到的商为3.14159,这就是圆周率较为精确的近似值,胡夫金字塔底部形为正方形,整个塔形为正四棱锥,经古代能工巧匠建设完成后,底座边长大约230米.因年久风化,胡夫金字塔现高约为136.5米,则与建成时比较顶端约剥落了( )
A.8米 B.10米 C.12米 D.14米
2.若水平放置的四边形按“斜二测画法”得到如图所示的直观图,其中,,,,则原四边形的面积为( )
A.12 B.6 C. D.
3.一个菱形的边长为,一个内角为,将菱形水平放置并且使较长的对角线成横向,则此菱形的直观图的面积为( ).
A. B. C. D.
4.如图,水平放置的四边形的斜二测直观图为矩形,已知,则四边形的周长为( )
A.20 B.12 C. D.
5.如图,一个水平放置的图形的直观图是一个等腰直角三角形,斜边长,那么原平面图形的面积是( )
A.2 B. C. D.
6.已知三棱锥P-ABC的四个顶点在球O的球面上,PA=PB=PC,△ABC是边长为2的正三角形,E,F分别是PA,AB的中点,∠CEF=90°,则球O的体积为
A. B. C. D.
7.如图所示,梯形是平面图形ABCD用斜二测画法得到的直观图,,,则平面图形ABCD的面积为( )
A. B.2 C. D.3
8.已知水平放置的按斜二测画法,得到如图所示的直观图,其中,,那么是一个( )
A.直角三角形 B.等边三角形
C.钝角三角形 D.三边互不相等的三角形
9.某圆锥母线长为2,底面半径为,则过该圆锥顶点的平面截此圆锥所得截面面积的最大值为( )
A.2 B. C. D.1
10.采用斜二测画法作一个五边形的直观图,则其直观图的面积是原来五边形面积的
A.倍 B.倍 C.倍 D.倍
11.某四棱锥的三视图如图所示,该四棱锥的最长棱的长度为( )
A.2 B. C. D.4
12.球面上两点之间的最短连线的长度,就是经过这两个点的大圆在这两点间的一段劣弧的长度(大圆就是经过球心的平面截球面所得的圆),我们把这个弧长叫做两点的球面距离.已知正的项点都在半径为的球面上,球心到所在平面距离为,则、两点间的球面距离为( )
A. B. C. D.
二、填空题
13.水平放置的平面四边形OABC,用斜二测画法画出它的直观图如图所示,此直观图恰好是个边长为2的正方形,则原平面四边形OABC的面积为_______.
14.如图,矩形是平面图形斜二测画法的直观图,且该直观图的面积为8,则平面图形的面积为___________.
15.已知四棱锥的底面是边长为的正方形,侧棱长均为.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为__________.
16.水平放置的矩形,,,则其直观图的面积为___________.
三、解答题
17.如图所示,三棱柱中,若,分别为,的中点,平面将三棱柱分成体积分别为,的两部分,那么等于多少
18.如图,是水平放置的斜二测画法的直观图,,,能否判断的形状并求边的实际长度是多少?
19.用斜二测画法画出如图所示的五边形的直观图.(不写作法,保留作图痕迹)
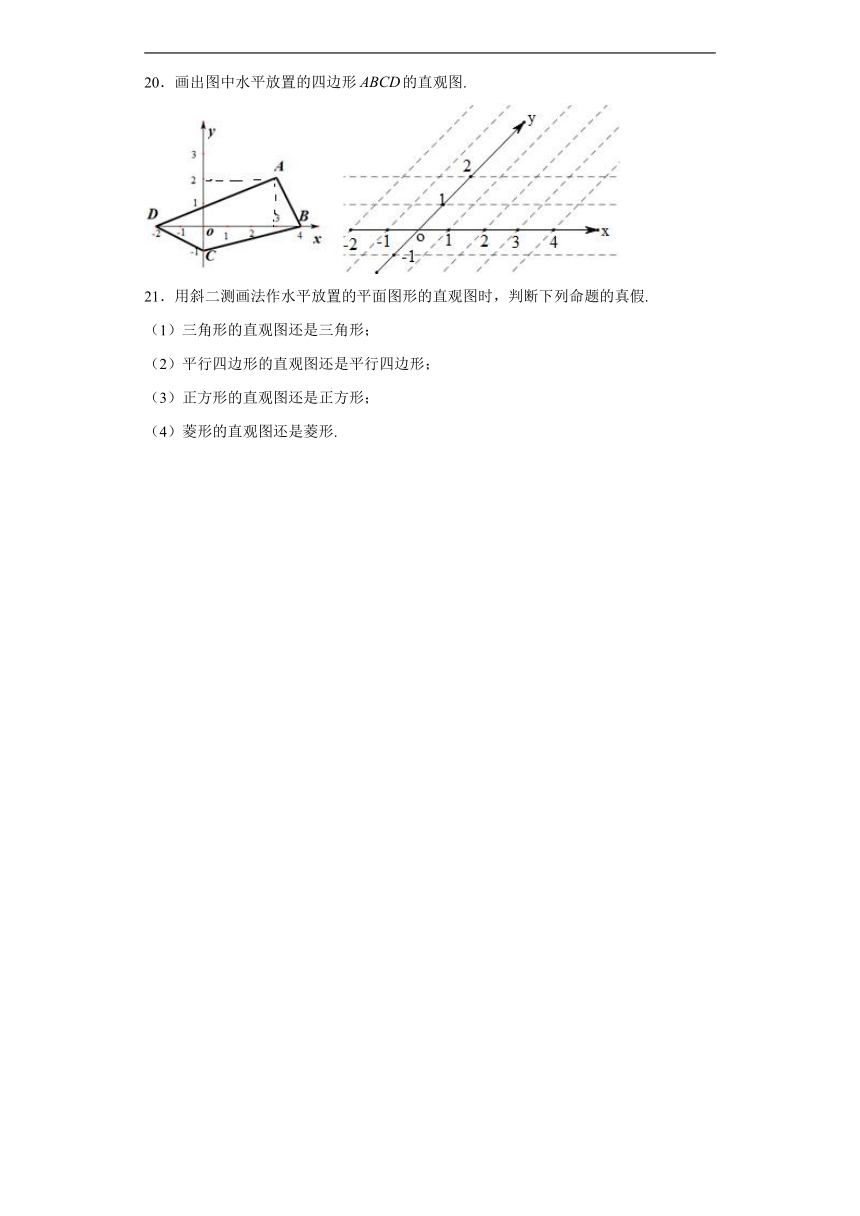
20.画出图中水平放置的四边形的直观图.
21.用斜二测画法作水平放置的平面图形的直观图时,判断下列命题的真假.
(1)三角形的直观图还是三角形;
(2)平行四边形的直观图还是平行四边形;
(3)正方形的直观图还是正方形;
(4)菱形的直观图还是菱形.
参考答案:
1.B
由题设条件求出建成时的高度,从而得出答案.
【详解】
,(米)
故选:B
2.C
由斜二测画法的直观图,还原原图形为直角梯形,从而即可计算原图形的面积.
【详解】
解:因为,,,,
所以由斜二测画法的直观图知可,
所以由斜二测画法的画法规则还原原图形,如图:
所以,,,,,
所以梯形的面积为.
故选:C.
3.C
根据斜二测画法的规则,求出对角线的长度,根据图形,求直观图的面积.
【详解】
由条件可知,较长的对角线的长度是,
较短的对角线的长度是,
根据斜二测画法的规则可知,,,菱形直观图的面积
故选:C
4.A
根据斜二测法求得且,进而求出,即可得结果.
【详解】
由题设,则原四边形中,又,
故,且,
所以四边形的周长为.
故选:A
5.B
根据斜二测画法可得原图形为直角三角形,运算即可得解.
【详解】
根据斜二测画法可得原图形为如图所示,
因为是等腰直角三角形,根据斜二测画法可得为直角三角形,
,,,
所以原平面图形的面积是.
故选:B.
6.D
先证得平面,再求得,从而得为正方体一部分,进而知正方体的体对角线即为球直径,从而得解.
【详解】
解法一:为边长为2的等边三角形,为正三棱锥,
,又,分别为、中点,
,,又,平面,平面,,为正方体一部分,,即 ,故选D.
解法二:
设,分别为中点,
,且,为边长为2的等边三角形,
又
中余弦定理,作于,,
为中点,,,
,,又,两两垂直,,,,故选D.
本题考查学生空间想象能力,补体法解决外接球问题.可通过线面垂直定理,得到三棱两两互相垂直关系,快速得到侧棱长,进而补体成正方体解决.
7.D
根据斜二测画法的规则确定原图形形状,结构得出面积.
【详解】
由三视图知原几何图形是直角梯形,如图,
,
面积为.
故选:D.
8.B
根据斜二测直观图的画法判断.
【详解】
在轴上,在轴,因此,在原图形中,,三角形为等边三角形.
故选:B.
9.A
如图截面为,P为MN的中点,设,,进而可得面积最大值.
【详解】
如图所示,截面为,P为MN的中点,设
,
当时,,此时截面面积最大.
故选:A
易错点睛:先求出面积的函数表达式进而判断最大值,本题容易误认为垂直于底面的截面面积最大.
10.D
根据斜二测画法中原图形面积与直观图面积的关系式即可得出答案.
【详解】
解:斜二测画法中原图形面积与直观图面积的关系式
所以
故选:D
11.C
由三视图得出该四棱锥为正四棱锥,再结合勾股定理得出答案.
【详解】
由三视图可知,该四棱锥为正四棱锥,正方形底面的边长为
侧棱长为,即最长棱的长度为
故选:C
12.C
设球心为点,计算出,利用扇形弧长公式可求得结果.
【详解】
设球心为点,平面截球所得截面圆的半径为,
由正弦定理可得,,
又,所以,为等边三角形,则,
因此,、两点间的球面距离为.
故选:C.
思路点睛:求球面距离,关键就是要求出球面上两点与球心所形成的角,结合扇形的弧长公式求解,同时在计算球的截面圆半径时,利用公式(其中为截面圆的半径,为球的半径,为球心到截面的距离)来计算.
13.
根据原图形与斜二测画法直观图之间的关系,还原原图形即可求解.
【详解】
,
还原回原图形后,
,
原图形的面积为
故答案为:
14.
根据直观图形和原图形面积之间的比例关系求解即可.
【详解】
根据直观图与原图的面积比值为定值,可得平面图形的面积为.
故答案为:.
15..
根据棱锥的结构特点,确定所求的圆柱的高和底面半径.
【详解】
由题意四棱锥的底面是边长为的正方形,侧棱长均为,借助勾股定理,可知四棱锥的高为,.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,圆柱的底面半径为,一个底面的圆心为四棱锥底面的中心,故圆柱的高为,故圆柱的体积为.
本题主要考查了圆柱与四棱锥的组合,考查了空间想象力,属于基础题.
16.
作出矩形的斜二测直观图,结合平行四边形的面积公式可求得结果.
【详解】
利用斜二测画法作出直观图,如图所示,产生平行四边形,
其中,,,
过点作于,则,
则.
故答案为:.
17.
如图,分别延长到,到,到,且,,,根据体积的大小关系得到答案.
【详解】
如图,分别延长到,到,到,且,,,连接,,,则得到三棱柱,且.
延长,,则与相交于点.
因为,所以.
连接,,则,所以,故
本题考查了组合体的体积比,意在考查学生的空间想象能力和计算能力.
18.答案见解析
由斜二测画法规则知:,从而易得边的实际长度.
【详解】
根据斜二测画法规则知:,故为直角三角形,
中,,,故.
结论点睛:(1)还原图形的过程是画直观图的逆过程,关键是找与轴、轴平行的直线或线段.平行于轴的线段长度不变,平行于轴的线段还原时长度变为原来的倍,由此确定图形的各个顶点,顺次连接即可;
(2)求图形的面积,关键是能先正确画出图形,然后求出相应边的长度,再利用公式求解;
(3)原图的面积与直观图的面积之间的关系为.
19.答案见解析﹒
根据斜二测画法作图即可.
【详解】
①如图(1),将A点和原点O重合,AB和x轴重合,AE与y轴重合.通过C分别作x轴、y轴的垂线,垂足分别为H、I,通过D分别作x轴、y轴的垂线,垂足分别为F、G;
②如图(2),作坐标系,轴和轴夹角为45°,在轴上取点,使得:与重合,,,;
③如图(2),在轴上取点,使得:,,;
④如图(2),过作轴平行线,过作轴平行线,两平行线交于;过作轴平行线,过作轴平行线,两平行线交于;
⑤如图(2),依次连接、、、即可完成作图.
20.图见解析.
在四边形中,过作出轴的垂直确定坐标,进而利用斜二测画法画出直观图.
【详解】
由斜二测画法:纵向减半,横向不变;即可知A、C在对应点,而B、D对应点位置不变,如下图示:
21.(1)真命题;(2)真命题;(3)假命题;(4)假命题.
根据三角形、平行四边形、正方形、菱形的直观图的性质,判断出命题的真假性.
【详解】
(1)三角形的直观图还是三角形,为真命题.
(2)平行四边形的直观图还是平行四边形,为真命题.
(3)正方形的直观图,边长不全相等,不是正方形,所以命题为假命题.
(4)菱形的直观图,边长不全相等,不是菱形,所以命题为假命题.
本小题主要考查斜二测画法,属于基础题.
一、单选题
1.埃及金字塔是古埃及的帝王(法老)陵墓,世界七大奇迹之一,其中较为著名的是胡夫金字塔.令人吃惊的并不仅仅是胡夫金字塔的雄壮身姿,还有发生在胡夫金字塔上的数字“巧合”.如胡夫金字塔的底部周长如果除以其高度的两倍,得到的商为3.14159,这就是圆周率较为精确的近似值,胡夫金字塔底部形为正方形,整个塔形为正四棱锥,经古代能工巧匠建设完成后,底座边长大约230米.因年久风化,胡夫金字塔现高约为136.5米,则与建成时比较顶端约剥落了( )
A.8米 B.10米 C.12米 D.14米
2.若水平放置的四边形按“斜二测画法”得到如图所示的直观图,其中,,,,则原四边形的面积为( )
A.12 B.6 C. D.
3.一个菱形的边长为,一个内角为,将菱形水平放置并且使较长的对角线成横向,则此菱形的直观图的面积为( ).
A. B. C. D.
4.如图,水平放置的四边形的斜二测直观图为矩形,已知,则四边形的周长为( )
A.20 B.12 C. D.
5.如图,一个水平放置的图形的直观图是一个等腰直角三角形,斜边长,那么原平面图形的面积是( )
A.2 B. C. D.
6.已知三棱锥P-ABC的四个顶点在球O的球面上,PA=PB=PC,△ABC是边长为2的正三角形,E,F分别是PA,AB的中点,∠CEF=90°,则球O的体积为
A. B. C. D.
7.如图所示,梯形是平面图形ABCD用斜二测画法得到的直观图,,,则平面图形ABCD的面积为( )
A. B.2 C. D.3
8.已知水平放置的按斜二测画法,得到如图所示的直观图,其中,,那么是一个( )
A.直角三角形 B.等边三角形
C.钝角三角形 D.三边互不相等的三角形
9.某圆锥母线长为2,底面半径为,则过该圆锥顶点的平面截此圆锥所得截面面积的最大值为( )
A.2 B. C. D.1
10.采用斜二测画法作一个五边形的直观图,则其直观图的面积是原来五边形面积的
A.倍 B.倍 C.倍 D.倍
11.某四棱锥的三视图如图所示,该四棱锥的最长棱的长度为( )
A.2 B. C. D.4
12.球面上两点之间的最短连线的长度,就是经过这两个点的大圆在这两点间的一段劣弧的长度(大圆就是经过球心的平面截球面所得的圆),我们把这个弧长叫做两点的球面距离.已知正的项点都在半径为的球面上,球心到所在平面距离为,则、两点间的球面距离为( )
A. B. C. D.
二、填空题
13.水平放置的平面四边形OABC,用斜二测画法画出它的直观图如图所示,此直观图恰好是个边长为2的正方形,则原平面四边形OABC的面积为_______.
14.如图,矩形是平面图形斜二测画法的直观图,且该直观图的面积为8,则平面图形的面积为___________.
15.已知四棱锥的底面是边长为的正方形,侧棱长均为.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为__________.
16.水平放置的矩形,,,则其直观图的面积为___________.
三、解答题
17.如图所示,三棱柱中,若,分别为,的中点,平面将三棱柱分成体积分别为,的两部分,那么等于多少
18.如图,是水平放置的斜二测画法的直观图,,,能否判断的形状并求边的实际长度是多少?
19.用斜二测画法画出如图所示的五边形的直观图.(不写作法,保留作图痕迹)
20.画出图中水平放置的四边形的直观图.
21.用斜二测画法作水平放置的平面图形的直观图时,判断下列命题的真假.
(1)三角形的直观图还是三角形;
(2)平行四边形的直观图还是平行四边形;
(3)正方形的直观图还是正方形;
(4)菱形的直观图还是菱形.
参考答案:
1.B
由题设条件求出建成时的高度,从而得出答案.
【详解】
,(米)
故选:B
2.C
由斜二测画法的直观图,还原原图形为直角梯形,从而即可计算原图形的面积.
【详解】
解:因为,,,,
所以由斜二测画法的直观图知可,
所以由斜二测画法的画法规则还原原图形,如图:
所以,,,,,
所以梯形的面积为.
故选:C.
3.C
根据斜二测画法的规则,求出对角线的长度,根据图形,求直观图的面积.
【详解】
由条件可知,较长的对角线的长度是,
较短的对角线的长度是,
根据斜二测画法的规则可知,,,菱形直观图的面积
故选:C
4.A
根据斜二测法求得且,进而求出,即可得结果.
【详解】
由题设,则原四边形中,又,
故,且,
所以四边形的周长为.
故选:A
5.B
根据斜二测画法可得原图形为直角三角形,运算即可得解.
【详解】
根据斜二测画法可得原图形为如图所示,
因为是等腰直角三角形,根据斜二测画法可得为直角三角形,
,,,
所以原平面图形的面积是.
故选:B.
6.D
先证得平面,再求得,从而得为正方体一部分,进而知正方体的体对角线即为球直径,从而得解.
【详解】
解法一:为边长为2的等边三角形,为正三棱锥,
,又,分别为、中点,
,,又,平面,平面,,为正方体一部分,,即 ,故选D.
解法二:
设,分别为中点,
,且,为边长为2的等边三角形,
又
中余弦定理,作于,,
为中点,,,
,,又,两两垂直,,,,故选D.
本题考查学生空间想象能力,补体法解决外接球问题.可通过线面垂直定理,得到三棱两两互相垂直关系,快速得到侧棱长,进而补体成正方体解决.
7.D
根据斜二测画法的规则确定原图形形状,结构得出面积.
【详解】
由三视图知原几何图形是直角梯形,如图,
,
面积为.
故选:D.
8.B
根据斜二测直观图的画法判断.
【详解】
在轴上,在轴,因此,在原图形中,,三角形为等边三角形.
故选:B.
9.A
如图截面为,P为MN的中点,设,,进而可得面积最大值.
【详解】
如图所示,截面为,P为MN的中点,设
,
当时,,此时截面面积最大.
故选:A
易错点睛:先求出面积的函数表达式进而判断最大值,本题容易误认为垂直于底面的截面面积最大.
10.D
根据斜二测画法中原图形面积与直观图面积的关系式即可得出答案.
【详解】
解:斜二测画法中原图形面积与直观图面积的关系式
所以
故选:D
11.C
由三视图得出该四棱锥为正四棱锥,再结合勾股定理得出答案.
【详解】
由三视图可知,该四棱锥为正四棱锥,正方形底面的边长为
侧棱长为,即最长棱的长度为
故选:C
12.C
设球心为点,计算出,利用扇形弧长公式可求得结果.
【详解】
设球心为点,平面截球所得截面圆的半径为,
由正弦定理可得,,
又,所以,为等边三角形,则,
因此,、两点间的球面距离为.
故选:C.
思路点睛:求球面距离,关键就是要求出球面上两点与球心所形成的角,结合扇形的弧长公式求解,同时在计算球的截面圆半径时,利用公式(其中为截面圆的半径,为球的半径,为球心到截面的距离)来计算.
13.
根据原图形与斜二测画法直观图之间的关系,还原原图形即可求解.
【详解】
,
还原回原图形后,
,
原图形的面积为
故答案为:
14.
根据直观图形和原图形面积之间的比例关系求解即可.
【详解】
根据直观图与原图的面积比值为定值,可得平面图形的面积为.
故答案为:.
15..
根据棱锥的结构特点,确定所求的圆柱的高和底面半径.
【详解】
由题意四棱锥的底面是边长为的正方形,侧棱长均为,借助勾股定理,可知四棱锥的高为,.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,圆柱的底面半径为,一个底面的圆心为四棱锥底面的中心,故圆柱的高为,故圆柱的体积为.
本题主要考查了圆柱与四棱锥的组合,考查了空间想象力,属于基础题.
16.
作出矩形的斜二测直观图,结合平行四边形的面积公式可求得结果.
【详解】
利用斜二测画法作出直观图,如图所示,产生平行四边形,
其中,,,
过点作于,则,
则.
故答案为:.
17.
如图,分别延长到,到,到,且,,,根据体积的大小关系得到答案.
【详解】
如图,分别延长到,到,到,且,,,连接,,,则得到三棱柱,且.
延长,,则与相交于点.
因为,所以.
连接,,则,所以,故
本题考查了组合体的体积比,意在考查学生的空间想象能力和计算能力.
18.答案见解析
由斜二测画法规则知:,从而易得边的实际长度.
【详解】
根据斜二测画法规则知:,故为直角三角形,
中,,,故.
结论点睛:(1)还原图形的过程是画直观图的逆过程,关键是找与轴、轴平行的直线或线段.平行于轴的线段长度不变,平行于轴的线段还原时长度变为原来的倍,由此确定图形的各个顶点,顺次连接即可;
(2)求图形的面积,关键是能先正确画出图形,然后求出相应边的长度,再利用公式求解;
(3)原图的面积与直观图的面积之间的关系为.
19.答案见解析﹒
根据斜二测画法作图即可.
【详解】
①如图(1),将A点和原点O重合,AB和x轴重合,AE与y轴重合.通过C分别作x轴、y轴的垂线,垂足分别为H、I,通过D分别作x轴、y轴的垂线,垂足分别为F、G;
②如图(2),作坐标系,轴和轴夹角为45°,在轴上取点,使得:与重合,,,;
③如图(2),在轴上取点,使得:,,;
④如图(2),过作轴平行线,过作轴平行线,两平行线交于;过作轴平行线,过作轴平行线,两平行线交于;
⑤如图(2),依次连接、、、即可完成作图.
20.图见解析.
在四边形中,过作出轴的垂直确定坐标,进而利用斜二测画法画出直观图.
【详解】
由斜二测画法:纵向减半,横向不变;即可知A、C在对应点,而B、D对应点位置不变,如下图示:
21.(1)真命题;(2)真命题;(3)假命题;(4)假命题.
根据三角形、平行四边形、正方形、菱形的直观图的性质,判断出命题的真假性.
【详解】
(1)三角形的直观图还是三角形,为真命题.
(2)平行四边形的直观图还是平行四边形,为真命题.
(3)正方形的直观图,边长不全相等,不是正方形,所以命题为假命题.
(4)菱形的直观图,边长不全相等,不是菱形,所以命题为假命题.
本小题主要考查斜二测画法,属于基础题.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
