1.2.4 绝对值 课件(共35页)
图片预览









文档简介
(共35张PPT)
第一章 有理数
人教版 七年级上
精品同步教学课件
1.2.4 绝对值
0
6
-1
-2
-3
-4
-5
-6
1
2
3
4
5
│-5│=5
│4│=4
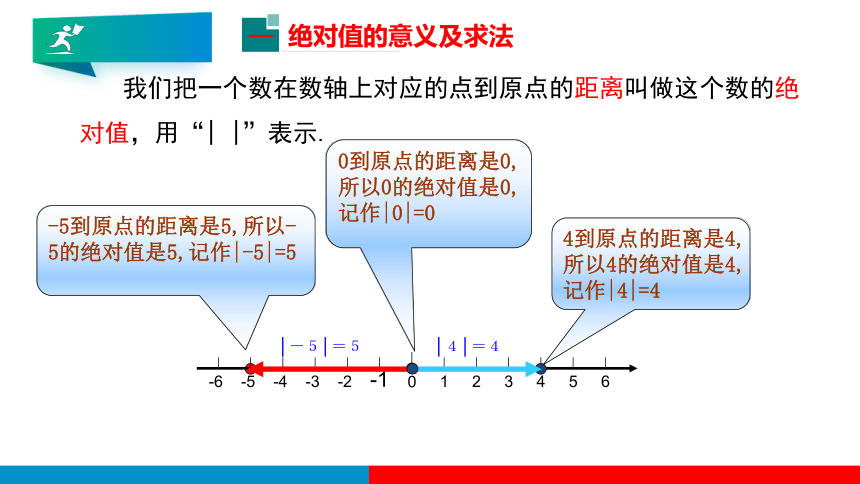
4到原点的距离是4,所以4的绝对值是4,记作|4|=4
-5到原点的距离是5,所以-5的绝对值是5,记作|-5|=5
我们把一个数在数轴上对应的点到原点的距离叫做这个数的绝对值,用“| |”表示.
0到原点的距离是0,所以0的绝对值是0,记作|0|=0
绝对值的意义及求法
一
利用数轴上点到原点的距离口答
|5|=
|3.5|=
|-3|=
|-4.5|=
|0|=
0
1
0
0
0
0
5
3.5
-3
-4.5
5
3.5
3
4.5
0
说一说
绝对值的性质及应用
二
|5|=5 |-3|=3
|3.5|= 3.5 |-10|=10
|50|=50 |-4.5|=4.5
|100|=100 |-500|=500
|0|=0 …..
思考: 一个正数的绝对值是什么?
一个负数的绝对值是什么?
0的绝对值是什么?
问题:观察这些表示绝对值的数,它们有什么共同点?
结论1:一个正数的绝对值是正数.
一个负数的绝对值是正数.
0的绝对值是0.
结论2:一个正数的绝对值是它本身.
一个负数的绝对值是它的相反数.
|a|≥0
任何一个有理数的绝对值都是非负数!
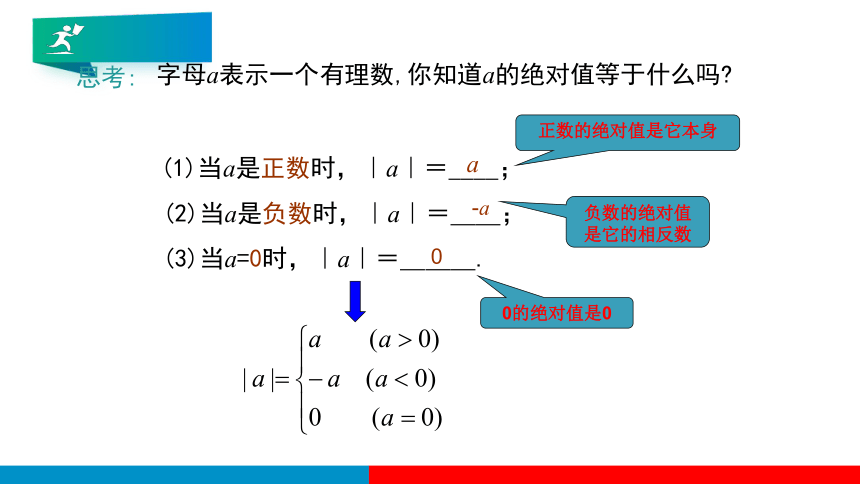
正数的绝对值是它本身
(1)当a是正数时,|a|=____;
(2)当a是负数时,|a|=__;
(3)当a=0时,|a|=___.
a
-a
0
0的绝对值是0
负数的绝对值是它的相反数
思考:
字母a表示一个有理数,你知道a的绝对值等于什么吗
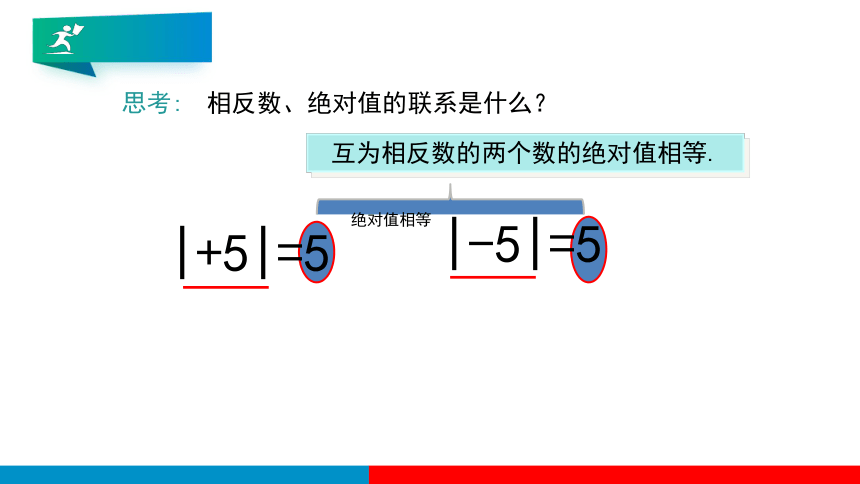
相反数、绝对值的联系是什么?
互为相反数的两个数的绝对值相等.
|-5|=5
|+5|=5
绝对值相等
思考:
(1)若a=-b,则|a|=|b|.
(2)若|a|=|b|,则a=b.
(3)若|a|=-a,则a必为负数.
判断下列说法是否正确.
√
×
×
练一练
例1 求下列各数的绝对值.
12, -7.5, 0.
解:
|12|=12;
| |= ;
|-7.5|=7.5;
|0|=0.
典例精析
练习
求下列各数的绝对值:
(1)+; (2)0; (3)-2; (4)-(-3).
解题秘方:紧扣绝对值的性质进行计算.
解:(1) = .
(2)|0|=0.
(3) =2.
(4)|-(-3)|=|+3|=3.
正数的绝对值是它本身.
0的绝对值是0.
负数的绝对值是它的相反数.
(1)绝对值等于0的数是___,
(2)绝对值等于5.25的正数是_____,
(3)绝对值等于5.25的负数是______,
(4)绝对值等于2的数是_______.
0
5.25
-5.25
2或-2
例2 填一填
易错提醒: 注意绝对值等于某个正数的数有两个,他们互为相反数,解题时不要遗漏负值.
解:根据题意可知
x-4=0,y-3=0,
所以x=4,y=3,故x+y=7.
归纳总结: 几个非负数的和为0,则这几个数都为0.
下列各式中无论m为何值,一定是正数的是( )
A.|m| B.|m+1|
C.| m |+1 D.-(-m)
练习
解题秘方:紧扣绝对值的非负性进行判断.
解:选项A中,当m=0 时,不符合题意;
选项B中,当m=-1 时,| m+1 |=0,不符合题意;
选项D中,-(-m)=m,显然不符合题意;
选项C中,因为| m | ≥ 0,所以| m |+1 ≥ 1,符合题意.
答案:C
练习:若a为任意有理数, 则-|-a|一定是( )
A.负数或零 B.负数
C.正数或零 D.正数
A
1.判断并改错:
(1)一个数的绝对值等于本身,则这个数一定是正数
( )
(2)一个数的绝对值等于它的相反数,这个数一定是
负数; ( )
(3)如果两个数的绝对值相等,那么这两个数一定
相等; ( )
(4)如果两个数不相等,那么这两个数的绝对值
一定不等; ( )
(5)有理数的绝对值一定是非负数. ( )
课堂检测
0
非负数
非正数
±2
2.____的相反数是它本身,_______的绝对值
是它本身,_______的绝对值是它的相反数.
3.|- |的相反数是 ;若| |=2,则
= _____.
-
4.化简:
-b
a-b
| b |= (b<0)
| a – b | = (a>b)
下图表示某一天我国5个城市的最低气温.
武汉5 ℃ 北京-10℃ 上海0℃ 广州10℃ 哈尔滨-20℃
借助数轴比较有理数的大小
三、
问题:你能将上述五个城市的最低气温按从低到高的顺序依次排列吗?
哈尔滨
-20℃
北京
-10℃
上海
0℃
武汉
5℃
广州
10℃
<
<
<
<
请大家思考这五个数的大小与它们在数轴上的位置有什么关系
越 来 越 大
哈尔滨
-20℃
北京
-10℃
上海
0℃
武汉
5℃
广州
10℃
<
<
<
<
-20 -10 0 5 10
●
●
●
●
●
有理数大小的比较方法1:
数轴比较法:
在数轴上表示的两个数,右边的数总比左边的数大.
-5 -4 -3 -2 -1 0 1 2 3 4 5
小 大
想一想
有没有最大的有理数 有没有最小的有理数 为什么
-5 -4 -3 -2 -1 0 1 2 3 4 5
●
●
●
●
-5 -3 0 4
例1 在数轴上表示数-3,-5,4,0,并比较它们的大小,将它们按从小到大的顺序用“<”号连接.
解:
-3,-5,4,0在数轴上表示如图:
将它们按从小到大的顺序排列为:
-5 <-3 <0 <4
典例精析
数轴法比较大小:1.画数轴2.定顺序3.定大小
如图,数轴上A,B,C三点表示的数分别为a,b,c,则它们的大小关系是( )
A.a>b>c B.b>c>a C.c>a>b D.b>a>c
针对训练
D
运用法则比较有理数的大小
二
结论:
(1)正数大于0,
(2)两个负数,绝对值大的反而小.
负数小于0,
正数大于负数;
问题:
对于正数、0、负数这三类数,它们之间有什么大小关系?
两个负数之间如何比较大小?
例2. 比较下列各数的大小.
解:先化简,-(-3)=3,
-(+2)=-2,
因为正数大于负数,所以3>-2,即
-(-3)>-(+2)
(1)-(-3)和-(+2);
异号两数比较要考虑它们的正负.
解:两个负数做比较,先求它们的绝对值.
同号两数比较要考虑它们的绝对值.
两负数相比较,绝对值大的反而小.
解:先化简:
比较下列各组数的大小:
(1)-和- ;(2)-|-5| 和0;(3)-和- .
解题秘方:利用正数>0> 负数,两个负数,绝对值大的反而小进行比较.
练习
解:(1)因为 = = , = = ,
且< ,所以- >- .
(2)因为-|-5|=-5,且-5<0,所以-|-5|<0.
(3)-= ,- =- .
因为正数大于负数,所以>- . 所以-> -.
下列判断,正确的是( )
A.若a>b,则│a│>│b│
B.若│a│>│b│,则a>b
C.若a<b<0,则│a│<│b│
D.若a>b>0,则│a│>│b│
能力提升
D
×
如a=1,b=-2
×
如a=-3,b=2
×
如a=-3,b=-2
√
课堂检测
2.比较下面各对数的大小,并说明理由:
>
<
>
<
1.在有理数0,│-(-3 )│,-│+1000│,-(-5)中最大的数是( )
A.0 B.-(-5) C.-│+1000│ D.│-(-3 )│
B
1.数轴上表示数a的点与原点的距离叫做数a的绝对值.
2.绝对值的性质
(1)|a|≥0;
(2)
课堂小结
课堂小结
3.比较有理数大小的方法.
方法①数轴法:数轴上表示的两个数,右边的总比左边的大.
方法②法则法:正数大于0,0大于负数,正数大于负数;
两个负数,绝对值大的反而小.
https://www.21cnjy.com/help/help_extract.php
第一章 有理数
人教版 七年级上
精品同步教学课件
1.2.4 绝对值
0
6
-1
-2
-3
-4
-5
-6
1
2
3
4
5
│-5│=5
│4│=4
4到原点的距离是4,所以4的绝对值是4,记作|4|=4
-5到原点的距离是5,所以-5的绝对值是5,记作|-5|=5
我们把一个数在数轴上对应的点到原点的距离叫做这个数的绝对值,用“| |”表示.
0到原点的距离是0,所以0的绝对值是0,记作|0|=0
绝对值的意义及求法
一
利用数轴上点到原点的距离口答
|5|=
|3.5|=
|-3|=
|-4.5|=
|0|=
0
1
0
0
0
0
5
3.5
-3
-4.5
5
3.5
3
4.5
0
说一说
绝对值的性质及应用
二
|5|=5 |-3|=3
|3.5|= 3.5 |-10|=10
|50|=50 |-4.5|=4.5
|100|=100 |-500|=500
|0|=0 …..
思考: 一个正数的绝对值是什么?
一个负数的绝对值是什么?
0的绝对值是什么?
问题:观察这些表示绝对值的数,它们有什么共同点?
结论1:一个正数的绝对值是正数.
一个负数的绝对值是正数.
0的绝对值是0.
结论2:一个正数的绝对值是它本身.
一个负数的绝对值是它的相反数.
|a|≥0
任何一个有理数的绝对值都是非负数!
正数的绝对值是它本身
(1)当a是正数时,|a|=____;
(2)当a是负数时,|a|=__;
(3)当a=0时,|a|=___.
a
-a
0
0的绝对值是0
负数的绝对值是它的相反数
思考:
字母a表示一个有理数,你知道a的绝对值等于什么吗
相反数、绝对值的联系是什么?
互为相反数的两个数的绝对值相等.
|-5|=5
|+5|=5
绝对值相等
思考:
(1)若a=-b,则|a|=|b|.
(2)若|a|=|b|,则a=b.
(3)若|a|=-a,则a必为负数.
判断下列说法是否正确.
√
×
×
练一练
例1 求下列各数的绝对值.
12, -7.5, 0.
解:
|12|=12;
| |= ;
|-7.5|=7.5;
|0|=0.
典例精析
练习
求下列各数的绝对值:
(1)+; (2)0; (3)-2; (4)-(-3).
解题秘方:紧扣绝对值的性质进行计算.
解:(1) = .
(2)|0|=0.
(3) =2.
(4)|-(-3)|=|+3|=3.
正数的绝对值是它本身.
0的绝对值是0.
负数的绝对值是它的相反数.
(1)绝对值等于0的数是___,
(2)绝对值等于5.25的正数是_____,
(3)绝对值等于5.25的负数是______,
(4)绝对值等于2的数是_______.
0
5.25
-5.25
2或-2
例2 填一填
易错提醒: 注意绝对值等于某个正数的数有两个,他们互为相反数,解题时不要遗漏负值.
解:根据题意可知
x-4=0,y-3=0,
所以x=4,y=3,故x+y=7.
归纳总结: 几个非负数的和为0,则这几个数都为0.
下列各式中无论m为何值,一定是正数的是( )
A.|m| B.|m+1|
C.| m |+1 D.-(-m)
练习
解题秘方:紧扣绝对值的非负性进行判断.
解:选项A中,当m=0 时,不符合题意;
选项B中,当m=-1 时,| m+1 |=0,不符合题意;
选项D中,-(-m)=m,显然不符合题意;
选项C中,因为| m | ≥ 0,所以| m |+1 ≥ 1,符合题意.
答案:C
练习:若a为任意有理数, 则-|-a|一定是( )
A.负数或零 B.负数
C.正数或零 D.正数
A
1.判断并改错:
(1)一个数的绝对值等于本身,则这个数一定是正数
( )
(2)一个数的绝对值等于它的相反数,这个数一定是
负数; ( )
(3)如果两个数的绝对值相等,那么这两个数一定
相等; ( )
(4)如果两个数不相等,那么这两个数的绝对值
一定不等; ( )
(5)有理数的绝对值一定是非负数. ( )
课堂检测
0
非负数
非正数
±2
2.____的相反数是它本身,_______的绝对值
是它本身,_______的绝对值是它的相反数.
3.|- |的相反数是 ;若| |=2,则
= _____.
-
4.化简:
-b
a-b
| b |= (b<0)
| a – b | = (a>b)
下图表示某一天我国5个城市的最低气温.
武汉5 ℃ 北京-10℃ 上海0℃ 广州10℃ 哈尔滨-20℃
借助数轴比较有理数的大小
三、
问题:你能将上述五个城市的最低气温按从低到高的顺序依次排列吗?
哈尔滨
-20℃
北京
-10℃
上海
0℃
武汉
5℃
广州
10℃
<
<
<
<
请大家思考这五个数的大小与它们在数轴上的位置有什么关系
越 来 越 大
哈尔滨
-20℃
北京
-10℃
上海
0℃
武汉
5℃
广州
10℃
<
<
<
<
-20 -10 0 5 10
●
●
●
●
●
有理数大小的比较方法1:
数轴比较法:
在数轴上表示的两个数,右边的数总比左边的数大.
-5 -4 -3 -2 -1 0 1 2 3 4 5
小 大
想一想
有没有最大的有理数 有没有最小的有理数 为什么
-5 -4 -3 -2 -1 0 1 2 3 4 5
●
●
●
●
-5 -3 0 4
例1 在数轴上表示数-3,-5,4,0,并比较它们的大小,将它们按从小到大的顺序用“<”号连接.
解:
-3,-5,4,0在数轴上表示如图:
将它们按从小到大的顺序排列为:
-5 <-3 <0 <4
典例精析
数轴法比较大小:1.画数轴2.定顺序3.定大小
如图,数轴上A,B,C三点表示的数分别为a,b,c,则它们的大小关系是( )
A.a>b>c B.b>c>a C.c>a>b D.b>a>c
针对训练
D
运用法则比较有理数的大小
二
结论:
(1)正数大于0,
(2)两个负数,绝对值大的反而小.
负数小于0,
正数大于负数;
问题:
对于正数、0、负数这三类数,它们之间有什么大小关系?
两个负数之间如何比较大小?
例2. 比较下列各数的大小.
解:先化简,-(-3)=3,
-(+2)=-2,
因为正数大于负数,所以3>-2,即
-(-3)>-(+2)
(1)-(-3)和-(+2);
异号两数比较要考虑它们的正负.
解:两个负数做比较,先求它们的绝对值.
同号两数比较要考虑它们的绝对值.
两负数相比较,绝对值大的反而小.
解:先化简:
比较下列各组数的大小:
(1)-和- ;(2)-|-5| 和0;(3)-和- .
解题秘方:利用正数>0> 负数,两个负数,绝对值大的反而小进行比较.
练习
解:(1)因为 = = , = = ,
且< ,所以- >- .
(2)因为-|-5|=-5,且-5<0,所以-|-5|<0.
(3)-= ,- =- .
因为正数大于负数,所以>- . 所以-> -.
下列判断,正确的是( )
A.若a>b,则│a│>│b│
B.若│a│>│b│,则a>b
C.若a<b<0,则│a│<│b│
D.若a>b>0,则│a│>│b│
能力提升
D
×
如a=1,b=-2
×
如a=-3,b=2
×
如a=-3,b=-2
√
课堂检测
2.比较下面各对数的大小,并说明理由:
>
<
>
<
1.在有理数0,│-(-3 )│,-│+1000│,-(-5)中最大的数是( )
A.0 B.-(-5) C.-│+1000│ D.│-(-3 )│
B
1.数轴上表示数a的点与原点的距离叫做数a的绝对值.
2.绝对值的性质
(1)|a|≥0;
(2)
课堂小结
课堂小结
3.比较有理数大小的方法.
方法①数轴法:数轴上表示的两个数,右边的总比左边的大.
方法②法则法:正数大于0,0大于负数,正数大于负数;
两个负数,绝对值大的反而小.
https://www.21cnjy.com/help/help_extract.php
