《平行四边形的面积》(同步练习)-五年级上册数学 人教版 (含答案)
文档属性
| 名称 | 《平行四边形的面积》(同步练习)-五年级上册数学 人教版 (含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 110.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-28 17:21:58 | ||
图片预览


文档简介
《平行四边形的面积》(同步练习)-五年级上册数学人教版
一.填空题(共9小题)
1.一个平行四边形的面积比与它等底等高的三角形的面积多6平方厘米,则这个三角形的面积是 平方厘米,平行四边形的面积是 平方厘米。
2.我们数学学习中经常会用“转化”思想,比如学习平行四边形面积时,我们将它转化成长方形来学行四边形的底就是长方形的 ,平行四边形的高就是长方形的 ,然后推导出平行四边形的面积计算方法。请你举个利用转化思想来学习的例子: 。
3.一个平行四边形框架拉成一个长方形,它的周长 .(填变或不变)
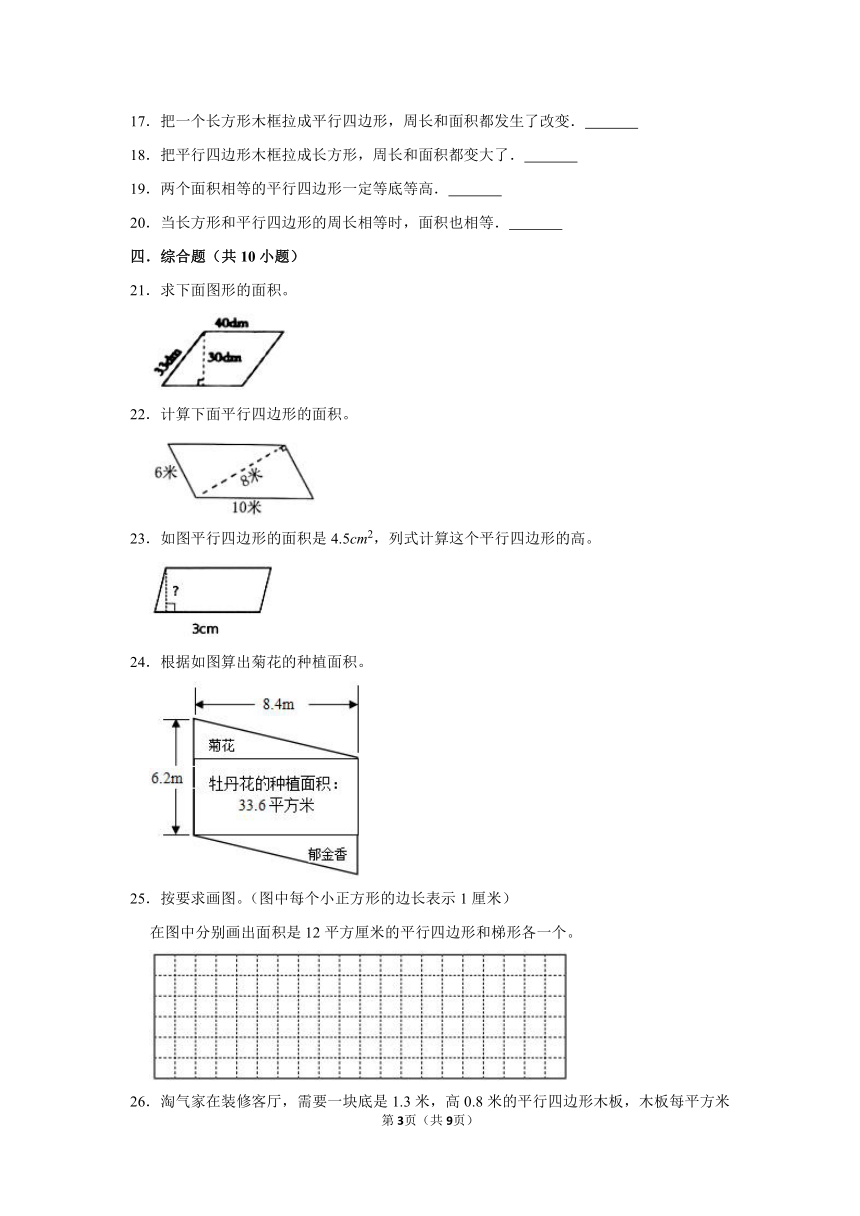
4.一个平行四边形的面积是9平方分米,底扩大到原来的4倍,高不变,扩大后的面积是 平方分米。
5.一个底是125米,高是80米的平行四边形花坛,面积是 平方米,等于 公顷。
6.一块平行四边形草地,底是3.6米,对应的高是2米,它的面积是 平方米。
7.小文把一个边长是6厘米的正方形框架,拉成了一个高是4厘米的平行四边形框架,这个平行四边形的周长是 厘米,面积是 平方厘米。
8.沿着平行四边形的一条高剪开,把两个剪开的图形拼成一个 ,从而推导出平行四边形面积的计算公式,应用了 的数学思想。
9.三角形的面积是6cm2,一条高是3cm,对应的底是 cm,与它等底等高的平行四边形的面积是 cm2。
二.选择题(共6小题)
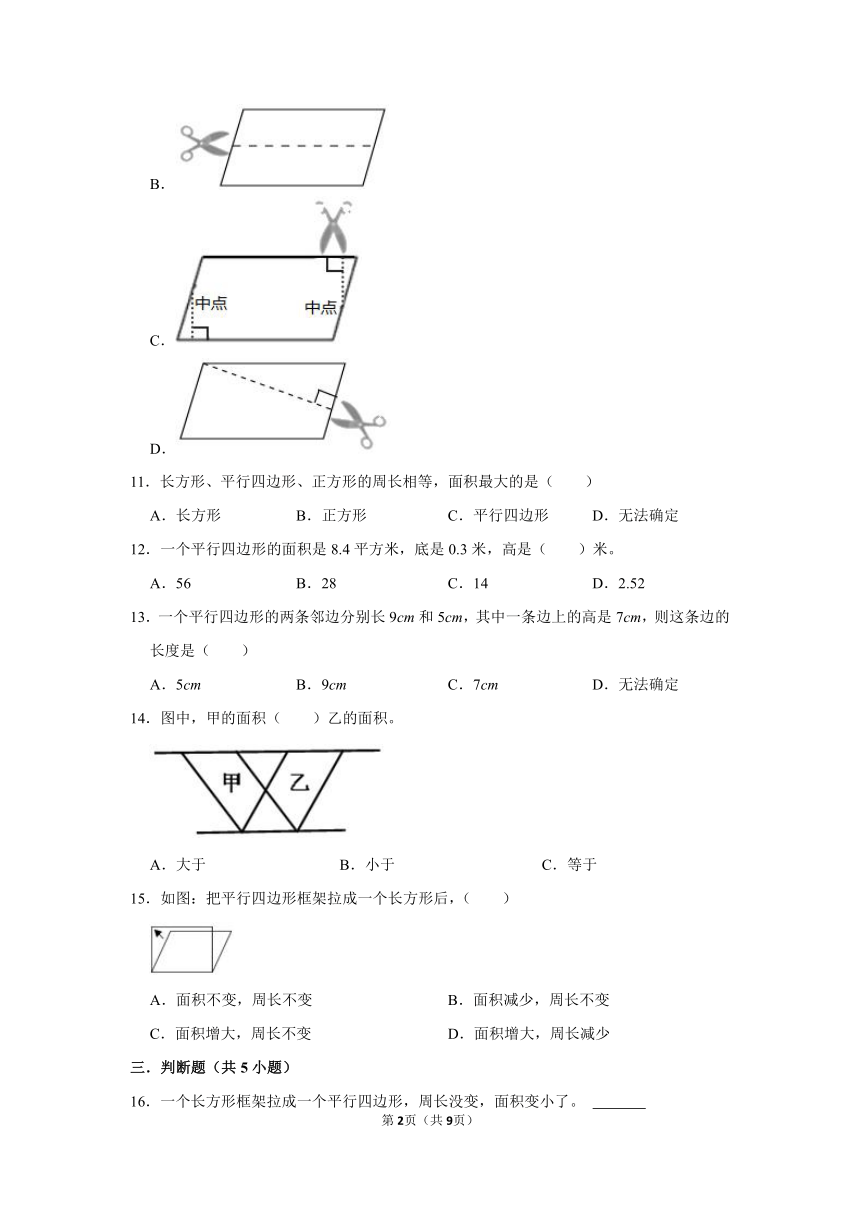
10.小明在研究平行四边形的面积时,想把一个平行四边形转化成一个长方形.下面的四种剪法中不能拼成长方形的是图( )
A.
B.
C.
D.
11.长方形、平行四边形、正方形的周长相等,面积最大的是( )
A.长方形 B.正方形 C.平行四边形 D.无法确定
12.一个平行四边形的面积是8.4平方米,底是0.3米,高是( )米。
A.56 B.28 C.14 D.2.52
13.一个平行四边形的两条邻边分别长9cm和5cm,其中一条边上的高是7cm,则这条边的长度是( )
A.5cm B.9cm C.7cm D.无法确定
14.图中,甲的面积( )乙的面积。
A.大于 B.小于 C.等于
15.如图:把平行四边形框架拉成一个长方形后,( )
A.面积不变,周长不变 B.面积减少,周长不变
C.面积增大,周长不变 D.面积增大,周长减少
三.判断题(共5小题)
16.一个长方形框架拉成一个平行四边形,周长没变,面积变小了。
17.把一个长方形木框拉成平行四边形,周长和面积都发生了改变.
18.把平行四边形木框拉成长方形,周长和面积都变大了.
19.两个面积相等的平行四边形一定等底等高.
20.当长方形和平行四边形的周长相等时,面积也相等.
四.综合题(共10小题)
21.求下面图形的面积。
22.计算下面平行四边形的面积。
23.如图平行四边形的面积是4.5cm2,列式计算这个平行四边形的高。
24.根据如图算出菊花的种植面积。
25.按要求画图。(图中每个小正方形的边长表示1厘米)
在图中分别画出面积是12平方厘米的平行四边形和梯形各一个。
26.淘气家在装修客厅,需要一块底是1.3米,高0.8米的平行四边形木板,木板每平方米的售价是120元,淘气家买这块木板需要多少元?
27.一个平行四边形的停车场,底是58米,高是26米,平均每个停车位的占地面积大约为14.5平方米,车辆通行道路的面积为203平方米,那么这个停车场可设置多少个停车位?
28.如果把一个长方形木框拉成一个平行四边形,周长和面积有变化吗?说说你的想法及理由。
29.如图:一块平行四边形的广告牌,每平方米大约要用油漆0.34kg.油漆工人带来15kg油漆,要刷完这块广告牌,这些油漆够吗?
30.一块平行四边形菜地,底400米,高150米,如果每公顷收白菜25吨,这块菜地能收白菜多少吨?
《平行四边形的面积》(同步练习)-五年级上册数学人教版
参考答案与试题解析
一.填空题(共9小题)
1.【解答】解:因为等底等高的平行四边形的面积是三角形面积的2倍,
6×2=12(平方厘米)
所以一个平行四边形的面积比与它等底等高的三角形的面积多6平方厘米,则这个三角形的面积是6平方厘米,平行四边形的面积是12平方厘米。
故答案为:6,12。
2.【解答】解:平行四边形的底就是长方形的长,平行四边形的高就是长方形的宽,然后推导出平行四边形的面积计算方法。请你举个利用转化思想来学习的例子:三角形面积公式的推导。
故答案为:长;宽;三角形面积公式的推导。
3.【解答】解:一个平行四边形框架拉成一个长方形,它的四条边的长度不变,进而根据周长的含义可得:周长不变,面积变大了;
故答案为:不变.
4.【解答】解:9×4=36(平方分米)
答:扩大后的面积是36平方分米。
故答案为:36。
5.【解答】解:125×80=10000(平方米)
10000平方米=1公顷
答:一个底是125米,高是80米的平行四边形花坛,面积是10000平方米,等于1公顷。
故答案为:10000;1。
6.【解答】解:3.6×2=7.2(平方米)
答:它的面积是7.2平方米。
故答案为:7.2。
7.【解答】解:6×4=24(厘米)
6×4=24(平方厘米)
答:这个平行四边形的周长是24厘米,面积是24平方厘米。
故答案为:24;24。
8.【解答】解:沿着平行四边形的一条高剪开,把两个剪开的图形拼成一个长方形,这个长方形的长等于平行四边形的底,长方形的宽等于平行四边形的高,根据长方形的面积公式推导出平行四边形的面积公式。这一过程应用了“转化”的思想方法。
故答案为:长方形,转化。
9.【解答】解:6×2÷3=4(厘米)
6×2=12(平方厘米)
答:对应的底是4cm,与它等底等高的平行四边形的面积是12cm2。
故答案为:4,12。
二.选择题(共6小题)
10.【解答】解:根据长方形的特征,长方形的对边平行且相等,
选项A:图形中是沿着高剪得,有直角,把剪下的左边图形平移到右边可以得到一个长方形.
选项B:图形中不是沿着高剪得,没有直角,把剪下的上面图形平移到下面不能得到一个长方形.
选项C,沿平行四边形的一边中点分别剪下了个直角三角形,通过旋转、平移后能够拼成一个长方形.
选项D,沿平行四边形的高剪开后,可以平成一个长方形.
故选:B.
11.【解答】解:因为周长相等的正方形、长方形、平行四边形中,正方形的面积最大。
故选:B。
12.【解答】解:8.4÷0.3=28(米)
答:高是28米。
故选:B。
13.【解答】解:一个平行四边形的两条邻边分别长9cm和5cm,其中一条边上的高是7cm,则这条边的长度是5cm。
故选:A。
14.【解答】解:因为等底等高的平行四边形的面积相等,所以甲的面积等于乙的面积。
故选:C。
15.【解答】解:平行四边形活动框架拉成长方形之后,每条边的长度不变,所以周长不变;
平行四边形活动框架拉成长方形之后,原来平行四边形的高比现在的长方形的高要小,但是对应的底的长度不变,又因为长方形是特殊的平行四边形,根据面积计算公式,平行四边形的面积=底×高,所以平行四边形的面积比长方形的面积要小.
所以一个平行四边形活动框架拉成长方形,原来平行四边形与现在长方形比较,周长不变,面积变大.
故选:C.
三.判断题(共5小题)
16.【解答】解:由于把长方形框架拉成平行四边形后,它的长和宽没变,所以周长不变,但是高变小了,所以面积就变小了。
因此,题干中的结论是正确的。
故答案为:√。
17.【解答】解:把长方形木框拉成平行四边形,四个边的长度没变,则其周长不变;但是它的高变短了,所以它的面积就变小了;
所以本题说法×;
故答案为:×.
18.【解答】解:因为把平行四边形木框拉成长方形,四个边的长度没变,则其周长不变;
但是它的高变长了,所以它的面积就变大了;
故答案为:×.
19.【解答】解:两个面积相等的平行四边形不一定等底等高.
故答案为:×.
20.【解答】解:因为当长方形和平行四边形的周长相等时,
则它们的边长可能相等,但高不一定相等,所以面积也就不一定相等;
故答案为:×.
四.综合题(共10小题)
21.【解答】解:40×30=1200(平方分米)
答:平行四边形的面积是1200平方分米。
22.【解答】解:6×8=48(平方米)
答:平行四边形的面积是48平方米。
23.【解答】解:4.5÷3=1.5(厘米)
答:这个平行四边形的高是1.5厘米。
24.【解答】解:(6.2×8.4﹣33.6)÷2
=(52.08﹣33.6)÷2
=18.48÷2
=9.24(平方米)
答:菊花的种植面积是9.24平方米。
25.【解答】解:
(画法不唯一)
26.【解答】解:1.3×0.8×120
=1.04×120
=124.8(元)
答:淘气家买这块木板需要124.8元。
27.【解答】解:(58×26﹣203)÷14.5
=(1508﹣203)÷14.5
=1305÷14.5
=90(个)
答:这个停车场可设置90个停车位。
28.【解答】解:把长方形木框拉成平行四边形,四个边的长度没变,则其周长不变;但是它的高变短了,所以它的面积就变小了。
29.【解答】解:10×4×0.34
=40×0.34
=13.6(千克)
13.6千克<15千克
答:这些油漆够.
30.【解答】解:400×150=60000(平方米))
60000平方米=6公顷
6×25=150(吨)
答:这块菜地能收白菜150吨。
第1页(共1页)
一.填空题(共9小题)
1.一个平行四边形的面积比与它等底等高的三角形的面积多6平方厘米,则这个三角形的面积是 平方厘米,平行四边形的面积是 平方厘米。
2.我们数学学习中经常会用“转化”思想,比如学习平行四边形面积时,我们将它转化成长方形来学行四边形的底就是长方形的 ,平行四边形的高就是长方形的 ,然后推导出平行四边形的面积计算方法。请你举个利用转化思想来学习的例子: 。
3.一个平行四边形框架拉成一个长方形,它的周长 .(填变或不变)
4.一个平行四边形的面积是9平方分米,底扩大到原来的4倍,高不变,扩大后的面积是 平方分米。
5.一个底是125米,高是80米的平行四边形花坛,面积是 平方米,等于 公顷。
6.一块平行四边形草地,底是3.6米,对应的高是2米,它的面积是 平方米。
7.小文把一个边长是6厘米的正方形框架,拉成了一个高是4厘米的平行四边形框架,这个平行四边形的周长是 厘米,面积是 平方厘米。
8.沿着平行四边形的一条高剪开,把两个剪开的图形拼成一个 ,从而推导出平行四边形面积的计算公式,应用了 的数学思想。
9.三角形的面积是6cm2,一条高是3cm,对应的底是 cm,与它等底等高的平行四边形的面积是 cm2。
二.选择题(共6小题)
10.小明在研究平行四边形的面积时,想把一个平行四边形转化成一个长方形.下面的四种剪法中不能拼成长方形的是图( )
A.
B.
C.
D.
11.长方形、平行四边形、正方形的周长相等,面积最大的是( )
A.长方形 B.正方形 C.平行四边形 D.无法确定
12.一个平行四边形的面积是8.4平方米,底是0.3米,高是( )米。
A.56 B.28 C.14 D.2.52
13.一个平行四边形的两条邻边分别长9cm和5cm,其中一条边上的高是7cm,则这条边的长度是( )
A.5cm B.9cm C.7cm D.无法确定
14.图中,甲的面积( )乙的面积。
A.大于 B.小于 C.等于
15.如图:把平行四边形框架拉成一个长方形后,( )
A.面积不变,周长不变 B.面积减少,周长不变
C.面积增大,周长不变 D.面积增大,周长减少
三.判断题(共5小题)
16.一个长方形框架拉成一个平行四边形,周长没变,面积变小了。
17.把一个长方形木框拉成平行四边形,周长和面积都发生了改变.
18.把平行四边形木框拉成长方形,周长和面积都变大了.
19.两个面积相等的平行四边形一定等底等高.
20.当长方形和平行四边形的周长相等时,面积也相等.
四.综合题(共10小题)
21.求下面图形的面积。
22.计算下面平行四边形的面积。
23.如图平行四边形的面积是4.5cm2,列式计算这个平行四边形的高。
24.根据如图算出菊花的种植面积。
25.按要求画图。(图中每个小正方形的边长表示1厘米)
在图中分别画出面积是12平方厘米的平行四边形和梯形各一个。
26.淘气家在装修客厅,需要一块底是1.3米,高0.8米的平行四边形木板,木板每平方米的售价是120元,淘气家买这块木板需要多少元?
27.一个平行四边形的停车场,底是58米,高是26米,平均每个停车位的占地面积大约为14.5平方米,车辆通行道路的面积为203平方米,那么这个停车场可设置多少个停车位?
28.如果把一个长方形木框拉成一个平行四边形,周长和面积有变化吗?说说你的想法及理由。
29.如图:一块平行四边形的广告牌,每平方米大约要用油漆0.34kg.油漆工人带来15kg油漆,要刷完这块广告牌,这些油漆够吗?
30.一块平行四边形菜地,底400米,高150米,如果每公顷收白菜25吨,这块菜地能收白菜多少吨?
《平行四边形的面积》(同步练习)-五年级上册数学人教版
参考答案与试题解析
一.填空题(共9小题)
1.【解答】解:因为等底等高的平行四边形的面积是三角形面积的2倍,
6×2=12(平方厘米)
所以一个平行四边形的面积比与它等底等高的三角形的面积多6平方厘米,则这个三角形的面积是6平方厘米,平行四边形的面积是12平方厘米。
故答案为:6,12。
2.【解答】解:平行四边形的底就是长方形的长,平行四边形的高就是长方形的宽,然后推导出平行四边形的面积计算方法。请你举个利用转化思想来学习的例子:三角形面积公式的推导。
故答案为:长;宽;三角形面积公式的推导。
3.【解答】解:一个平行四边形框架拉成一个长方形,它的四条边的长度不变,进而根据周长的含义可得:周长不变,面积变大了;
故答案为:不变.
4.【解答】解:9×4=36(平方分米)
答:扩大后的面积是36平方分米。
故答案为:36。
5.【解答】解:125×80=10000(平方米)
10000平方米=1公顷
答:一个底是125米,高是80米的平行四边形花坛,面积是10000平方米,等于1公顷。
故答案为:10000;1。
6.【解答】解:3.6×2=7.2(平方米)
答:它的面积是7.2平方米。
故答案为:7.2。
7.【解答】解:6×4=24(厘米)
6×4=24(平方厘米)
答:这个平行四边形的周长是24厘米,面积是24平方厘米。
故答案为:24;24。
8.【解答】解:沿着平行四边形的一条高剪开,把两个剪开的图形拼成一个长方形,这个长方形的长等于平行四边形的底,长方形的宽等于平行四边形的高,根据长方形的面积公式推导出平行四边形的面积公式。这一过程应用了“转化”的思想方法。
故答案为:长方形,转化。
9.【解答】解:6×2÷3=4(厘米)
6×2=12(平方厘米)
答:对应的底是4cm,与它等底等高的平行四边形的面积是12cm2。
故答案为:4,12。
二.选择题(共6小题)
10.【解答】解:根据长方形的特征,长方形的对边平行且相等,
选项A:图形中是沿着高剪得,有直角,把剪下的左边图形平移到右边可以得到一个长方形.
选项B:图形中不是沿着高剪得,没有直角,把剪下的上面图形平移到下面不能得到一个长方形.
选项C,沿平行四边形的一边中点分别剪下了个直角三角形,通过旋转、平移后能够拼成一个长方形.
选项D,沿平行四边形的高剪开后,可以平成一个长方形.
故选:B.
11.【解答】解:因为周长相等的正方形、长方形、平行四边形中,正方形的面积最大。
故选:B。
12.【解答】解:8.4÷0.3=28(米)
答:高是28米。
故选:B。
13.【解答】解:一个平行四边形的两条邻边分别长9cm和5cm,其中一条边上的高是7cm,则这条边的长度是5cm。
故选:A。
14.【解答】解:因为等底等高的平行四边形的面积相等,所以甲的面积等于乙的面积。
故选:C。
15.【解答】解:平行四边形活动框架拉成长方形之后,每条边的长度不变,所以周长不变;
平行四边形活动框架拉成长方形之后,原来平行四边形的高比现在的长方形的高要小,但是对应的底的长度不变,又因为长方形是特殊的平行四边形,根据面积计算公式,平行四边形的面积=底×高,所以平行四边形的面积比长方形的面积要小.
所以一个平行四边形活动框架拉成长方形,原来平行四边形与现在长方形比较,周长不变,面积变大.
故选:C.
三.判断题(共5小题)
16.【解答】解:由于把长方形框架拉成平行四边形后,它的长和宽没变,所以周长不变,但是高变小了,所以面积就变小了。
因此,题干中的结论是正确的。
故答案为:√。
17.【解答】解:把长方形木框拉成平行四边形,四个边的长度没变,则其周长不变;但是它的高变短了,所以它的面积就变小了;
所以本题说法×;
故答案为:×.
18.【解答】解:因为把平行四边形木框拉成长方形,四个边的长度没变,则其周长不变;
但是它的高变长了,所以它的面积就变大了;
故答案为:×.
19.【解答】解:两个面积相等的平行四边形不一定等底等高.
故答案为:×.
20.【解答】解:因为当长方形和平行四边形的周长相等时,
则它们的边长可能相等,但高不一定相等,所以面积也就不一定相等;
故答案为:×.
四.综合题(共10小题)
21.【解答】解:40×30=1200(平方分米)
答:平行四边形的面积是1200平方分米。
22.【解答】解:6×8=48(平方米)
答:平行四边形的面积是48平方米。
23.【解答】解:4.5÷3=1.5(厘米)
答:这个平行四边形的高是1.5厘米。
24.【解答】解:(6.2×8.4﹣33.6)÷2
=(52.08﹣33.6)÷2
=18.48÷2
=9.24(平方米)
答:菊花的种植面积是9.24平方米。
25.【解答】解:
(画法不唯一)
26.【解答】解:1.3×0.8×120
=1.04×120
=124.8(元)
答:淘气家买这块木板需要124.8元。
27.【解答】解:(58×26﹣203)÷14.5
=(1508﹣203)÷14.5
=1305÷14.5
=90(个)
答:这个停车场可设置90个停车位。
28.【解答】解:把长方形木框拉成平行四边形,四个边的长度没变,则其周长不变;但是它的高变短了,所以它的面积就变小了。
29.【解答】解:10×4×0.34
=40×0.34
=13.6(千克)
13.6千克<15千克
答:这些油漆够.
30.【解答】解:400×150=60000(平方米))
60000平方米=6公顷
6×25=150(吨)
答:这块菜地能收白菜150吨。
第1页(共1页)
