1.4.1 第1课时 有理数的乘法法则 课件(共33页)
文档属性
| 名称 | 1.4.1 第1课时 有理数的乘法法则 课件(共33页) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-28 20:21:12 | ||
图片预览








文档简介
(共33张PPT)
1.4 有理数的乘除法
第一章 有理数
第1课时 有理数的乘法法则
人教版 七年级上
精品同步教学课件
如图,一只蜗牛沿直线 l爬行,它现在的位置在l上的点O.
l
O
1.如果一只蜗牛向右爬行2cm记为+2cm,那么向左爬行2cm应该记为 .
2.如果3分钟以后记为+3分钟,那么3分钟以前应该记为 .
-2cm
-3分钟
探究1
2
0
2
6
4
l
结果:3分钟后在l上点O 边 cm处
表示: .
右
6
(+2)×(+3)= 6
(1)
(1)如果蜗牛一直以每分钟2 cm的速度向右爬行,3分钟后它在什么位置?
规定:向左为负,向右为正.
现在前为负,现在后为正.
为了区分方向与时间:
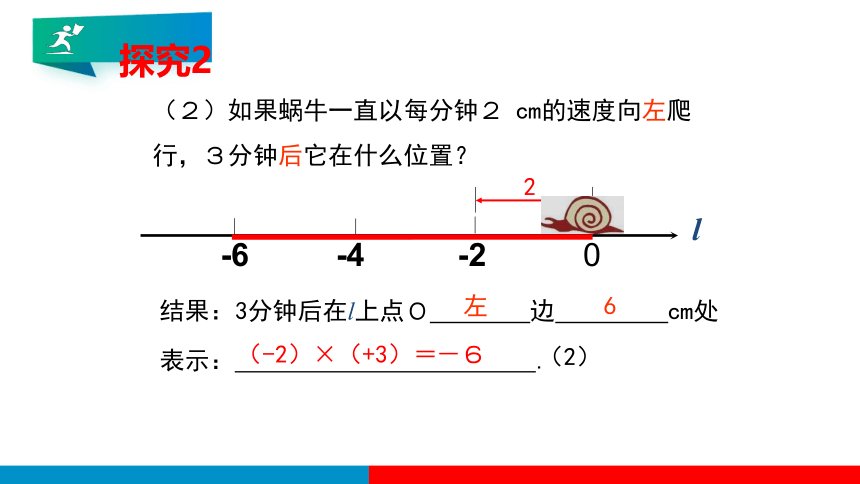
(2)如果蜗牛一直以每分钟2 cm的速度向左爬行,3分钟后它在什么位置?
探究2
-6
-4
0
-2
2
l
结果:3分钟后在l上点O 边 cm处
左
6
表示: .
(-2)×(+3)=
(2)
-6
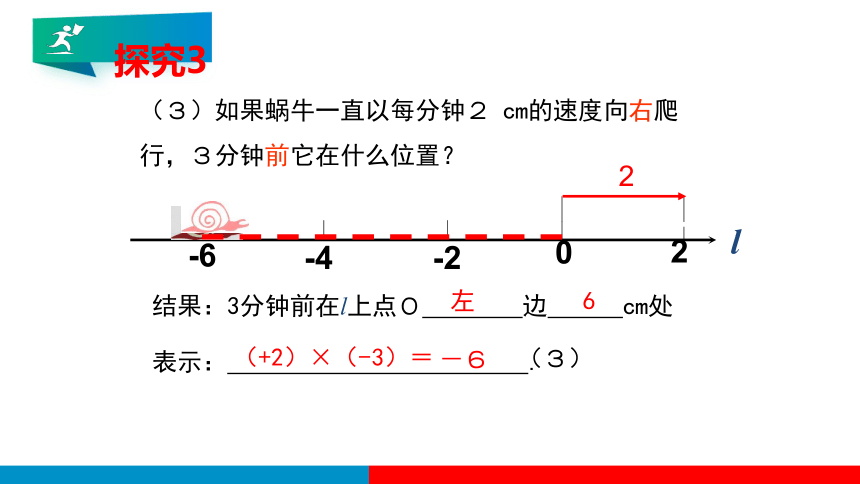
(3)如果蜗牛一直以每分钟2 cm的速度向右爬行,3分钟前它在什么位置?
探究3
2
-6
-4
0
-2
2
l
结果:3分钟前在l上点O 边 cm处
表示: .
(+2)×(-3)=
-6
左
6
(3)
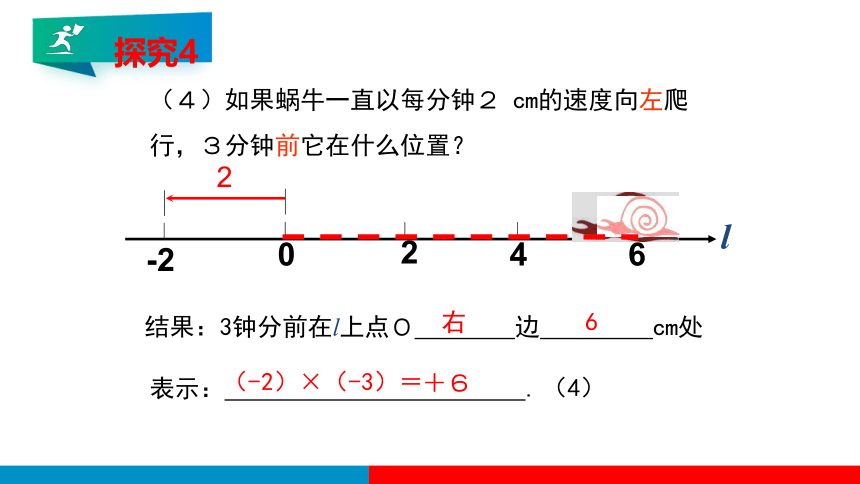
(4)如果蜗牛一直以每分钟2 cm的速度向左爬行,3分钟前它在什么位置?
探究4
2
0
2
6
4
-2
l
结果:3钟分前在l上点O 边 cm处
右
6
表示: .
(-2)×(-3)=
(4)
+6
答:结果都是仍在原处,即结果都是 ,
若用式子表达:
探究5
(5)原地不动或运动时间为零,结果是什么?
0×3=0;0×(-3)=0;
2×0=0;(-2)×0=0.
0
O
1.正数乘正数积为__数;负数乘负数积为__数;
2.负数乘正数积为__数;正数乘负数积为__数;
3.乘积的绝对值等于各乘数绝对值的__.
正
正
负
负
积
(同号得正)
(异号得负)
4.零与任何数相乘或任何数与零相乘结果是 .
零
根据上面结果可知:
(+2)×(+3)=+6 (-2)×(-3)=+6
(-2)×(+3)=-6 (+2)×(-3)=-6
2×0=0 (-2)×0=0
有理数乘法法则
1.两数相乘,同号得正,异号得负,并把绝对值相乘.
2.任何数同0相乘,都得0.
讨论:
(1)若a<0,b>0,则ab 0 ;
(2)若a<0,b<0,则ab 0 ;
(3)若ab>0,则a、b应满足什么条件?
(4)若ab<0,则a、b应满足什么条件?
<
>
a、b同号
a、b异号
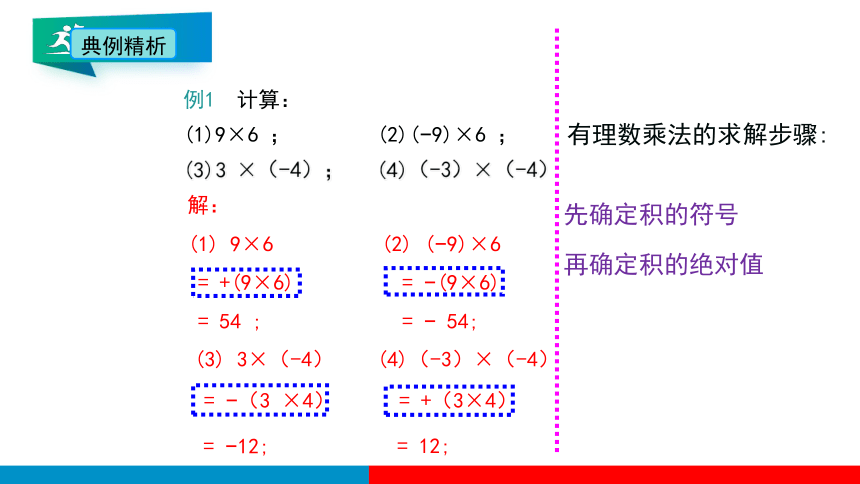
例1 计算:
(1)9×6 ; (2)( 9)×6 ;
解:
(1) 9×6 (2) ( 9)×6
= +(9×6) = (9×6)
= 54 ; = 54;
(3) 3×(-4) (4)(-3)×(-4)
= 12;
有理数乘法的求解步骤:
先确定积的符号
再确定积的绝对值
(3)3 ×(-4); (4)(-3)×(-4)
= (3 ×4) = +(3×4)
= 12;
典例精析
练习
计算下列各题:
(1)×; (2)1 ×;
(3)×(-1); (4)×0.
解题秘方:两个数相乘,根据乘法法则,先确定积的符号,再把绝对值相乘即可.
解:(1) × = × = ;
(2)1 × = -× =- ;
(3) ×(-1) = ;
(4) ×0 = 0.
任何数与-1相乘都等于它的相反数.
根据下列条件,判断a,b 的正负性.
(1)a+b < 0,ab > 0;
(2)a-b < 0,ab < 0.
解题秘方:先根据两个数积的符号判断出两个数是同号还是异号,再根据两个数和(差)的符号,判断两个数的正负性.
练习
解:(1)因为ab>0,所以a,b 同号.
又因为a+b<0,所以a,b 同为负.
(2)因为ab<0,所以a,b 异号.
又因为a-b<0,所以a所以a 为负,b 为正.
计算并观察结果有何特点?
(1) ×2; (2)(-0.25)×(-4)
要点:有理数中,乘积是1的两个数互为倒数.
思考:数a(a≠0)的倒数是什么
(a≠0时,a的倒数是 )
倒数
二
说出下列各数的倒数:
1,-1, ,- ,5,-5,0.75,-
1,
-1,
3,
-3,
练一练
思考:
1.一个数和它倒数的符号相同吗?
2.倒数等于它本身的数有哪些?
3.有没有数没有倒数?
倒数与相反数之间的关系
不同点 相同点
定义 表示 性质 判定 倒数 乘积是1 的两个数互为倒数. a(a ≠ 0)的倒数是. 若a, b互为倒数, 则a·b=1. 若a·b=1, 则a,b互为倒数. 都成对出现.
相反数 只有符号不同的两个数叫做互为相反数. a 的相反数是-a. 若a,b互为相反数, 则a+b=0. 若a+b=0, 则a,b互为相反数. 求下列各数的倒数.
(1)-4;(2)-;(3)0.125;(4)1 ;(5)-1.
练习
解题秘方:利用倒数的定义确定各数的倒数.
解:(1)-4 的倒数是-;
(2)- 的倒数是- ;
(3)0.125 的倒数是8;
(4)1的倒数是;
(5)-1 的倒数是-1.
倒数之间不能用等号,如-4的倒数是- ,不能用“-4=- ”表示- 4的倒数.
判断下列各式的积是正的还是负的?
2×3×4×(-5)
2×3×(-4)×(-5)
2×(-3)×(-4)×(-5)
(-2)×(-3)×(-4)×(-5)
7.8×(-8.1)×0×(-19.6)
负
正
负
正
零
思考:几个有理数相乘,因数都不为 0 时,积的符号怎样确定? 有一因数为 0 时,积是多少?
多个有理数相乘
几个不等于零的数相乘,积的符号由_____________决定.
当负因数有_____个时,积为负;
当负因数有_____个时,积为正.
要点归纳:
几个数相乘,如果其中有因数为0,_________
负因数的个数
奇数
偶数
积等于0
}
奇负偶正
例2 计算:
解:(1)原式
(2)原式
先确定积的符号
再确定积的绝对值
计算:
(1)(-5)×(-4)×(-2)×(-2);
(2)×××5;
(3) ××0.732×0.
解题秘方:利用多个有理数相乘的法则,先确定符号,再计算绝对值的乘积.
解:(1)(-5)×(-4)×(-2)×(-2)
=5×4×2×2=80.
(2) ×××5
=- × × ×5=-6.
(3) ××0.732×0 = 0.
例3 用正负数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km,气温的变化量为-6℃,攀登3km后,气温有什么变化?
解:(-6)×3=-18
答:气温下降18℃.
二
有理数的乘法的应用
商店降价销售某种商品,每件降5元,售出60件后,与按原价销售同样数量的商品相比,销售额有什么变化?
练一练
解:(-5)×60=-300(元)
答:销售额减少300元.
1.P32练习1口算
2.P32练习2计算
随堂练习
3.气象观测统计资料表明,在一般情况下,高度每上升1km,气温下降6℃.已知甲地现在地面气温为21℃,求甲地上空9km处的气温大约是多少?
解:(-6)×9=-54(℃);
21+(-54)=-33(℃).
答:甲地上空9km处的气温大约为-33℃.
课堂小结
有理数乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数同0相乘,都得0.
课堂小结
1.几个不是零的数相乘,负因数的个数为
奇数时积为负数
偶数时积为正数
2.几个数相乘若有因数为零则积为零.
3.有理数乘法的求解步骤:
有理数相乘,先确定积的符号,再确定积的绝对值.
https://www.21cnjy.com/help/help_extract.php
1.4 有理数的乘除法
第一章 有理数
第1课时 有理数的乘法法则
人教版 七年级上
精品同步教学课件
如图,一只蜗牛沿直线 l爬行,它现在的位置在l上的点O.
l
O
1.如果一只蜗牛向右爬行2cm记为+2cm,那么向左爬行2cm应该记为 .
2.如果3分钟以后记为+3分钟,那么3分钟以前应该记为 .
-2cm
-3分钟
探究1
2
0
2
6
4
l
结果:3分钟后在l上点O 边 cm处
表示: .
右
6
(+2)×(+3)= 6
(1)
(1)如果蜗牛一直以每分钟2 cm的速度向右爬行,3分钟后它在什么位置?
规定:向左为负,向右为正.
现在前为负,现在后为正.
为了区分方向与时间:
(2)如果蜗牛一直以每分钟2 cm的速度向左爬行,3分钟后它在什么位置?
探究2
-6
-4
0
-2
2
l
结果:3分钟后在l上点O 边 cm处
左
6
表示: .
(-2)×(+3)=
(2)
-6
(3)如果蜗牛一直以每分钟2 cm的速度向右爬行,3分钟前它在什么位置?
探究3
2
-6
-4
0
-2
2
l
结果:3分钟前在l上点O 边 cm处
表示: .
(+2)×(-3)=
-6
左
6
(3)
(4)如果蜗牛一直以每分钟2 cm的速度向左爬行,3分钟前它在什么位置?
探究4
2
0
2
6
4
-2
l
结果:3钟分前在l上点O 边 cm处
右
6
表示: .
(-2)×(-3)=
(4)
+6
答:结果都是仍在原处,即结果都是 ,
若用式子表达:
探究5
(5)原地不动或运动时间为零,结果是什么?
0×3=0;0×(-3)=0;
2×0=0;(-2)×0=0.
0
O
1.正数乘正数积为__数;负数乘负数积为__数;
2.负数乘正数积为__数;正数乘负数积为__数;
3.乘积的绝对值等于各乘数绝对值的__.
正
正
负
负
积
(同号得正)
(异号得负)
4.零与任何数相乘或任何数与零相乘结果是 .
零
根据上面结果可知:
(+2)×(+3)=+6 (-2)×(-3)=+6
(-2)×(+3)=-6 (+2)×(-3)=-6
2×0=0 (-2)×0=0
有理数乘法法则
1.两数相乘,同号得正,异号得负,并把绝对值相乘.
2.任何数同0相乘,都得0.
讨论:
(1)若a<0,b>0,则ab 0 ;
(2)若a<0,b<0,则ab 0 ;
(3)若ab>0,则a、b应满足什么条件?
(4)若ab<0,则a、b应满足什么条件?
<
>
a、b同号
a、b异号
例1 计算:
(1)9×6 ; (2)( 9)×6 ;
解:
(1) 9×6 (2) ( 9)×6
= +(9×6) = (9×6)
= 54 ; = 54;
(3) 3×(-4) (4)(-3)×(-4)
= 12;
有理数乘法的求解步骤:
先确定积的符号
再确定积的绝对值
(3)3 ×(-4); (4)(-3)×(-4)
= (3 ×4) = +(3×4)
= 12;
典例精析
练习
计算下列各题:
(1)×; (2)1 ×;
(3)×(-1); (4)×0.
解题秘方:两个数相乘,根据乘法法则,先确定积的符号,再把绝对值相乘即可.
解:(1) × = × = ;
(2)1 × = -× =- ;
(3) ×(-1) = ;
(4) ×0 = 0.
任何数与-1相乘都等于它的相反数.
根据下列条件,判断a,b 的正负性.
(1)a+b < 0,ab > 0;
(2)a-b < 0,ab < 0.
解题秘方:先根据两个数积的符号判断出两个数是同号还是异号,再根据两个数和(差)的符号,判断两个数的正负性.
练习
解:(1)因为ab>0,所以a,b 同号.
又因为a+b<0,所以a,b 同为负.
(2)因为ab<0,所以a,b 异号.
又因为a-b<0,所以a
计算并观察结果有何特点?
(1) ×2; (2)(-0.25)×(-4)
要点:有理数中,乘积是1的两个数互为倒数.
思考:数a(a≠0)的倒数是什么
(a≠0时,a的倒数是 )
倒数
二
说出下列各数的倒数:
1,-1, ,- ,5,-5,0.75,-
1,
-1,
3,
-3,
练一练
思考:
1.一个数和它倒数的符号相同吗?
2.倒数等于它本身的数有哪些?
3.有没有数没有倒数?
倒数与相反数之间的关系
不同点 相同点
定义 表示 性质 判定 倒数 乘积是1 的两个数互为倒数. a(a ≠ 0)的倒数是. 若a, b互为倒数, 则a·b=1. 若a·b=1, 则a,b互为倒数. 都成对出现.
相反数 只有符号不同的两个数叫做互为相反数. a 的相反数是-a. 若a,b互为相反数, 则a+b=0. 若a+b=0, 则a,b互为相反数. 求下列各数的倒数.
(1)-4;(2)-;(3)0.125;(4)1 ;(5)-1.
练习
解题秘方:利用倒数的定义确定各数的倒数.
解:(1)-4 的倒数是-;
(2)- 的倒数是- ;
(3)0.125 的倒数是8;
(4)1的倒数是;
(5)-1 的倒数是-1.
倒数之间不能用等号,如-4的倒数是- ,不能用“-4=- ”表示- 4的倒数.
判断下列各式的积是正的还是负的?
2×3×4×(-5)
2×3×(-4)×(-5)
2×(-3)×(-4)×(-5)
(-2)×(-3)×(-4)×(-5)
7.8×(-8.1)×0×(-19.6)
负
正
负
正
零
思考:几个有理数相乘,因数都不为 0 时,积的符号怎样确定? 有一因数为 0 时,积是多少?
多个有理数相乘
几个不等于零的数相乘,积的符号由_____________决定.
当负因数有_____个时,积为负;
当负因数有_____个时,积为正.
要点归纳:
几个数相乘,如果其中有因数为0,_________
负因数的个数
奇数
偶数
积等于0
}
奇负偶正
例2 计算:
解:(1)原式
(2)原式
先确定积的符号
再确定积的绝对值
计算:
(1)(-5)×(-4)×(-2)×(-2);
(2)×××5;
(3) ××0.732×0.
解题秘方:利用多个有理数相乘的法则,先确定符号,再计算绝对值的乘积.
解:(1)(-5)×(-4)×(-2)×(-2)
=5×4×2×2=80.
(2) ×××5
=- × × ×5=-6.
(3) ××0.732×0 = 0.
例3 用正负数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km,气温的变化量为-6℃,攀登3km后,气温有什么变化?
解:(-6)×3=-18
答:气温下降18℃.
二
有理数的乘法的应用
商店降价销售某种商品,每件降5元,售出60件后,与按原价销售同样数量的商品相比,销售额有什么变化?
练一练
解:(-5)×60=-300(元)
答:销售额减少300元.
1.P32练习1口算
2.P32练习2计算
随堂练习
3.气象观测统计资料表明,在一般情况下,高度每上升1km,气温下降6℃.已知甲地现在地面气温为21℃,求甲地上空9km处的气温大约是多少?
解:(-6)×9=-54(℃);
21+(-54)=-33(℃).
答:甲地上空9km处的气温大约为-33℃.
课堂小结
有理数乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数同0相乘,都得0.
课堂小结
1.几个不是零的数相乘,负因数的个数为
奇数时积为负数
偶数时积为正数
2.几个数相乘若有因数为零则积为零.
3.有理数乘法的求解步骤:
有理数相乘,先确定积的符号,再确定积的绝对值.
https://www.21cnjy.com/help/help_extract.php
