【解析版】江苏省泰州市2012-2013学年高一(上)期末数学试卷
文档属性
| 名称 | 【解析版】江苏省泰州市2012-2013学年高一(上)期末数学试卷 |  | |
| 格式 | zip | ||
| 文件大小 | 158.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-08-29 10:09:17 | ||
图片预览




文档简介
江苏省泰州市2012-2013学年高一(上)期末数学试卷
一、填空题:(本大题共14小题,每小题5分,共70分.请将答案填入答题纸填空题的相应答题线上.)
1.(5分)sin960°的值为 .
考点:
诱导公式的作用.
专题:
计算题.
分析:
利用诱导公式,先化为0°~360°的正弦,再转化为锐角的正弦,即可求得
解答:
解:由题意,sin960°=sin(720°+240°)=sin240°=sin(180°+60°)=﹣
故答案为:
点评:
本题的考点是诱导公式的应用,解题的关键是正确选用诱导公式转化.
2.(5分)函数的定义域是 (﹣∞,1) .
考点:
函数的定义域及其求法.
专题:
计算题.
分析:
根据二次根式的性质和分式的意义,被开方数大于等于0,分母不等于0,就可以求解.
解答:
解:依题意,得1﹣x>0,解得x<1,
∴函数的定义域是 (﹣∞,1)
故答案为:(﹣∞,1).
点评:
本题考查了函数自变量的取值范围:注意分式有意义,分母不为0;二次根式的被开方数是非负数.
3.(5分)已知幂函数y=f(x)的图象过点,则f(2)= 8 .
考点:
幂函数的概念、解析式、定义域、值域;函数的值.
专题:
函数的性质及应用.
分析:
设出幂函数的解析式,把点代入后求出幂指数的值,则解析式可求,从而求得f(2)的值.
解答:
解:设幂函数f(x)=xα,因为其图象过点,
所以,,解得:α=3.
所以,f(x)=x3.
则f(2)=23=8.
故答案为8.
点评:
本题考查了幂函数的概念,考查了代点求函数解析式,考查了函数值的求法,解答此题的关键是理解幂函数概念,此题是基础题.
4.(5分)若函数f(x)=x4+(m﹣1)x+1为偶函数,则实数m的值为 1 .
考点:
函数奇偶性的性质.
专题:
计算题;函数的性质及应用.
分析:
由已知可得f(﹣x)=f(x)对于任意的x都成立,代入即可求解m的值
解答:
解:∵f(x)=x4+(m﹣1)x+1为偶函数,
∴f(﹣x)=f(x)对于任意的x都成立
即(﹣x)4﹣(m﹣1)x+1=x4+(m﹣1)x+1
∴2(m﹣1)x=0对于任意x都成立
∴m=1
故答案为:1
点评:
本题主要考查了偶函数的定义的简单应用,属于基础试题
5.(5分)已知扇形的中心角为120°,半径为,则此扇形的面积为 π .
考点:
扇形面积公式.
分析:
利用扇形的面积计算公式即可得出.
解答:
解:∵弧度,∴此扇形的面积S====π.
故答案为π.
点评:
熟练掌握扇形的面积计算公式是解题的关键.
6.(5分)将函数y=sin2x的图象向右平移个单位所得函数的解析式为 y=sin(2x﹣) .
考点:
函数y=Asin(ωx+φ)的图象变换.
专题:
计算题.
分析:
左加右减上加下减的原则,直接求出将函数y=sin2x的图象向右平移个单位所得函数的解析式.
解答:
解:将函数y=sin2x的图象向右平移个单位所得函数的解析式:y=sin2(x﹣)=sin(2x﹣),
故答案为:y=sin(2x﹣).
点评:
本题主要考查三角函数的平移.三角函数的平移原则为左加右减上加下减.注意x前面的系数的应用.
7.(5分)= 6 .
考点:
对数的运算性质;有理数指数幂的化简求值.
专题:
函数的性质及应用.
分析:
利用指数幂和对数的运算性质即可得出.
解答:
解:原式=lg(4×52)+=lg102+22=2+4=6.
故答案为6.
点评:
熟练掌握指数幂和对数的运算性质是解题的关键.
8.(5分)在平面直角坐标系xoy中,已知以x轴为始边的角α、β的终边分别经过点(﹣4,3)、(3,4),则tan(α+β)= .
考点:
两角和与差的正切函数;任意角的三角函数的定义;同角三角函数间的基本关系.
专题:
三角函数的图像与性质.
分析:
由三角函数的定义可得tanα=,tanβ=,代入两角和的正切公式计算可得答案.
解答:
解:由题意结合三角函数的定义可得
tanα==,tanβ=,
由两角和的正切公式可得
tan(α+β)===,
故答案为:
点评:
本题考查三角函数的定义,以及两角和的正切公式,属基础题.
9.(5分)函数f(x)=|x+2|+x2的单调增区间是 (也对) .
考点:
函数单调性的判断与证明.
专题:
函数的性质及应用.
分析:
去掉绝对值符号把f(x)转化为分段函数,把各段中的单调区间求出来,然后即可得到答案.
解答:
解:f(x)==,
当x<﹣2时,f(x)=单调递减;
当x≥﹣2时,f(x)=在(﹣,+∞)上递增,在(﹣2,﹣)上递减,
综上知,f(x)的增区间为:(﹣,+∞).
点评:
本题考查绝对值函数单调区间的求法,该类问题常见方法为:作出图象,用图象求解;去绝对值转化为分段函数解决.
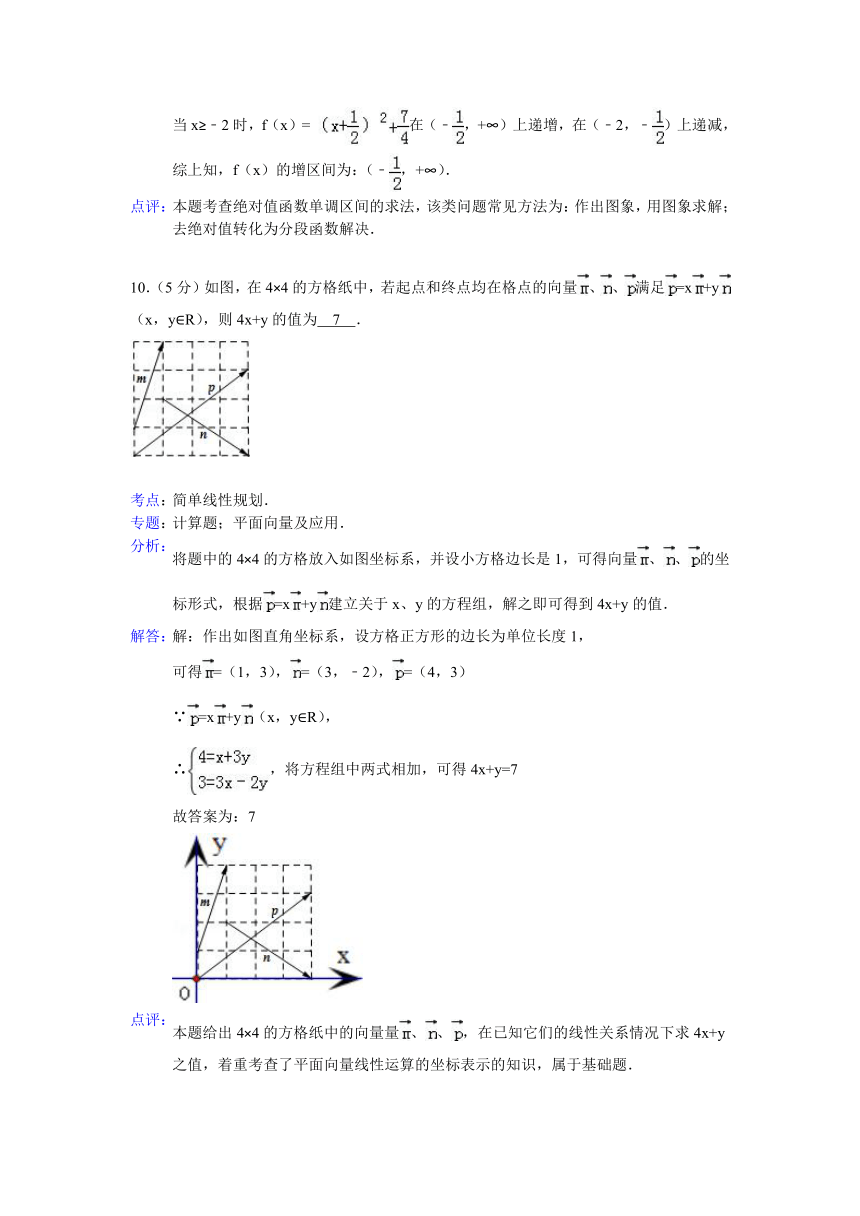
10.(5分)如图,在4×4的方格纸中,若起点和终点均在格点的向量、、满足=x+y(x,y∈R),则4x+y的值为 7 .
考点:
简单线性规划.
专题:
计算题;平面向量及应用.
分析:
将题中的4×4的方格放入如图坐标系,并设小方格边长是1,可得向量、、的坐标形式,根据=x+y建立关于x、y的方程组,解之即可得到4x+y的值.
解答:
解:作出如图直角坐标系,设方格正方形的边长为单位长度1,
可得=(1,3),=(3,﹣2),=(4,3)
∵=x+y(x,y∈R),
∴,将方程组中两式相加,可得4x+y=7
故答案为:7
点评:
本题给出4×4的方格纸中的向量量、、,在已知它们的线性关系情况下求4x+y之值,着重考查了平面向量线性运算的坐标表示的知识,属于基础题.
11.(5分)若函数f(x)=x2﹣2ax+b(a>1)的定义域与值域都是[1,a],则实数b= 5 .
考点:
函数的值域;函数的定义域及其求法.
专题:
函数的性质及应用.
分析:
首先求出函数的对称轴方程,由此判断函数在给定的定义域[1,a]内是减函数,再根据函数的值域也是[1,a],联立,可求b的值.
解答:
解:函数f(x)=x2﹣2ax+b(a>1)的对称轴方程为x=,
所以函数f(x)=x2﹣2ax+b在[1,a]上为减函数,
又函数在[1,a]上的值域也为[1,a],
则,即,
由①得:b=3a﹣1,代入②得:a2﹣3a+2=0,解得:a=1(舍),a=2.
把a=2代入b=3a﹣1得:b=5.
故答案为5.
点评:
本题考查了二次函数的单调性,考查了函数的值域的求法,考查了方程思想,解答此题的关键是判断函数在给定定义域内的单调性,此题是基础题.
12.(5分)已知直线与函数f(x)=cosx,g(x)=sin2x和h(x)=sinx的图象及x轴依次交于点P,M,N,Q,则PN2+MQ2的最小值为 .
考点:
二倍角的正弦;函数的值域;正弦函数的单调性.
分析:
正确画出三角函数的图象,进而由图象可列出式子表达已知条件,利用三角函数的单调性、有界性和二次函数的单调性即可得出最小值.
解答:
解:如图所示,
则PN2+MQ2=(cosx﹣sinx)2+sin22x=sin22x﹣sin2x+1=,
因此当时,则PN2+MQ2的最小值为.
故答案为.
点评:
熟练掌握数形结合的思想方法、三角函数的单调性、有界性和二次函数的单调性是解题的关键.
13.(5分)已知点G、H分别为△ABC的重心(三条中线的交点)、垂心(三条高所在直线的交点),若,则的值为 .
考点:
平面向量数量积的运算;三角形五心.
专题:
平面向量及应用.
分析:
利用三角形的重心和垂心的性质、向量的运算法则、数量积的定义即可得出.
解答:
解:如图所示:
设AE、AD分别为BC边上的中线、高,则,.
∴==
====﹣.
故答案为.
点评:
熟练掌握三角形的重心和垂心的性质、向量的运算法则、数量积的定义是解题的关键.
14.(5分)已知函数f(x)=mx﹣1,g(x)=x2﹣(m+1)x﹣1,若对任意的x0>0,f(x0)与g(x0)的值不异号,则实数m的值为 .
考点:
其他不等式的解法;函数单调性的性质;二次函数的性质;函数的零点.
专题:
计算题;不等式的解法及应用.
分析:
通过m大于0,等于0,小于0,分别判断对任意的x0>0,f(x0)与g(x0)的值不异号,是否成立,求出m的值即可.
解答:
解:当m=0时,不满足条件(可知(x)=mx﹣1与X Y轴都有交点)
当m>0时,画出两函数图象需满足g()=0且<得出m=;
当m<0时,因为一次函数f(x)=mx﹣1在x趋近于正无穷大时候为负无穷大,
而二次函数g(x)=x2﹣(m+1)x﹣1,在x趋近于正无穷大时为正无穷大,不满足要求.
综上:m=.
故答案为:.
点评:
本题考查一次函数与二次函数的图象的性质,函数的单调性,对称性,考查分析问题解决问题的能力.
二、解答题(本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤.)
15.(14分)已知集合A={x|2≤x≤6,x∈R},B={x|﹣1<x<5,x∈R},全集U=R.
(1)求A∩(CUB);
(2)若集合C={x|x<a,x∈R},A∩C=?,求实数a的取值范围.
考点:
交、并、补集的混合运算.
专题:
不等式的解法及应用.
分析:
(1)本题为集合的运算问题,结合数轴依据集合运算的定义即可求出集合A∩(CUB);
(2)利用数轴通过A∩C=?,直接求a的取值范围.
解答:
解:(1)∵B={x|﹣1<x<5,x∈R},
∴CUB={x|x≤﹣1或x≥5},…(4分)
∴A∩(CUB)={x|5≤x≤6}. …(8分)
(2)∵A={x|2≤x≤6,x∈R},
C={x|x<a,x∈R},A∩C=?,如图,
∴a的取值范围是a≤2. …(14分)
(不写等号扣2分)
点评:
本题考查集合的运算问题,考查数形结合思想解题,属基本运算的考查.
16.(14分)已知函数的部分图象如图所示.
(1)求A,ω的值;
(2)求f(x)的单调增区间;
(3)求f(x)在区间上的最大值和最小值.
考点:
y=Asin(ωx+φ)中参数的物理意义;正弦函数的定义域和值域;正弦函数的单调性.
专题:
计算题;三角函数的图像与性质.
分析:
(1)通过函数的图象直接求A,利用函数的周期即可求出ω的值;
(2)根据函数的单调增区间,直接求f(x)的单调增区间即可;
(3)通过x∈,求出函数的相位的范围,利用正弦函数的最值,直接求解f(x)的最大值和最小值.
解答:
解:(1)由图象知A=1,…(2分)
由图象得函数的最小正周期为,
则由得ω=2.…(4分)
(2)∵,
∴.
∴.
所以f(x)的单调递增区间为.…(9分)
(3)∵,∵,
∴.
∴.…(12分)
当,即时,f(x)取得最大值1;
当,即时,f(x)取得最小值.…(14分)
点评:
本题考查函数解析式的求法,正弦函数的单调性的应用,正弦函数的最值的求法,考查计算能力.
17.(14分)销售甲、乙两种商品所得利润分别是y1、y2万元,它们与投入资金x万元的关系分别为,y2=bx,(其中m,a,b都为常数),函数y1,y2对应的曲线C1、C2如图所示.
(1)求函数y1、y2的解析式;
(2)若该商场一共投资4万元经销甲、乙两种商品,求该商场所获利润的最大值.
考点:
根据实际问题选择函数类型;函数解析式的求解及常用方法.
专题:
函数的性质及应用.
分析:
(1)根据所给的图象知,两曲线的交点坐标为,由此列出关于m,a的方程组,解出m,a的值,即可得到函数y1、y2的解析式;
(2)对甲种商品投资x(万元),对乙种商品投资(4﹣x)(万元),根据公式可得甲、乙两种商品的总利润y(万元)关于x的函数表达式;再利用配方法确定函数的对称轴,结合函数的定义域,即可求得总利润y的最大值.
解答:
解:(1)由题意,解得,…(4分)
又由题意得(x≥0)…(7分)
(不写定义域扣一分)
(2)设销售甲商品投入资金x万元,则乙投入(4﹣x)万元
由(1)得,(0≤x≤4)…(10分)
令,则有=,,
当t=2即x=3时,y取最大值1.
答:该商场所获利润的最大值为1万元.…(14分)
(不答扣一分)
点评:
本题考查了函数模型的构建以及换元法、配方法求函数的最值,体现用数学知识解决实际问题,属于基础题.
18.(16分)已知向量=(1,cosα),=(1,sinβ),=(3,1),且(+)∥.
(1)若,求cos2β的值;
(2)证明:不存在角α,使得等式|+|=|﹣|成立;
(3)求?﹣2的最小值.
考点:
平行向量与共线向量;二次函数在闭区间上的最值.
专题:
函数的性质及应用.
分析:
(1)由题意可得当可得sinβ,由二倍角公式可得cos2β;
(2)假设成立,由数量积的运算可得,即cosα=﹣3,矛盾;
(3)由(1)可得,代入可得所求式子为关于cosα的二次函数,进而可得最值.
解答:
解:∵,=(3,1),且()∥.∴…(3分)
(1)∵,∴,∴,∴…(6分)
(2)假设存在角α使得等式成立则有
∴,∴cosα=﹣3,不成立,∴不存在角α使得等式成立.…(11分)
(3)∵∴,
∴,又﹣1≤cosα≤1,∴,…(13分)
∴当cosα=1时,. …(16分)
点评:
本题考查平行向量,以及二次函数在闭区间的最值,属基础题.
19.(16分)已知函数f(x)=x2,g(x)=ax+3(a∈R).
(1)记函数F(x)=f(x)﹣g(x),
(i)判断函数F(x)的零点个数;
(ii)若函数|F(x)|在[0,1]上是减函数,求实数a的取值范围.
(2)设.若对于函数y=G(x)图象上异于原点O的任意一点P,在函数y=G(x)图象上总存在另一点Q,使得,且PQ的中点在y轴上,求a的取值范围.
考点:
平面向量数量积的运算;函数单调性的判断与证明;根的存在性及根的个数判断.
专题:
计算题;函数的性质及应用;平面向量及应用.
分析:
(1)利用函数F(x)=f(x)﹣g(x)求出表达式,
(i)利用判别式的符号,直接判断函数F(x)的零点个数;
(ii)通过函数|F(x)|在[0,1]上是减函数,化简函数的表达式,利用函数的对称轴,以及1处的函数值,列出不等式组,求实数a的取值范围.
(2)通过.求出函数y=G(x)的表达式,设出点P的坐标、Q的坐标,通过,且PQ的中点在y轴上,求出a的取值范围.
解答:
解:(1)(i)F(x)=x2﹣ax﹣3
∵∴函数F(x)有2个零点. …(4分)
(ii) ,当a≤0时,图象为:
当a>0时,图象为:
由题意.解得﹣2≤a≤0…(8分)
(2),
由题意易知P,Q两点在y轴的两侧,不妨设P点坐标在y轴的左侧,设,
当﹣1<x1<0,则,恒成立,…(12分)
当x1≤﹣1,则设点Q(﹣x1,﹣ax1+3),恒成立,
∴ax1>2恒成立,∵x1≤﹣1,
∴恒成立,只要∴,…(14分)
∵x1≤﹣1,∴,
∴a<﹣2. …(16分)
点评:
本题考查函数的零点,函数与方程的关系的应用,恒成立问题的应用,平面向量的数量积的应用,考查分析问题解决问题的能力.
20.(16分)已知函数f(x)是区间D?[0,+∞)上的增函数,若f(x)可表示为f(x)=f1(x)+f2(x),且满足下列条件:①f1(x)是D上的增函数;②f2(x)是D上的减函数;③函数f2(x)的值域A?[0,+∞),则称函数f(x)是区间D上的“偏增函数”.
(1)(i) 问函数y=sinx+cosx是否是区间上的“偏增函数”?并说明理由;
(ii)证明函数y=sinx是区间上的“偏增函数”.
(2)证明:对任意的一次函数f(x)=kx+b(k>0),必存在一个区间D?[0,+∞),使f(x)为D上的“偏增函数”.
考点:
奇偶性与单调性的综合.
专题:
新定义;函数的性质及应用.
分析:
(1)(i)记f1(x)=sinx,f2(x)=cosx,根据偏增函数的定义及正余弦函数的性质可作出判断;(ii)f(x)=(sinx﹣cosx)+cosx,记,根据偏增函数的定义可证明;
(2)分情况讨论:①当b>0时,令f1(x)=(k+1)x,f2(x)=﹣x+b,取D=(0,b);②当b≤0时,取c>0,且满足c+b>0,令f1(x)=(k+1)x﹣c,f2(x)=﹣x+b+c,D=(0,b+c),根据偏增函数定义即可证明;
解答:
(1)解:(i) y=sinx+cosx是区间上的“偏增函数”.
记f1(x)=sinx,f2(x)=cosx,显然f1(x)=sinx在上单调递增,f2(x)=cosx在上单调递减,
且f2(x)=cosx∈(,1)?[0,+∞),
又在上单调递增,
故y=sinx+cosx是区间上的“偏增函数”.
(ii)证明:,
记,
显然在上单调递增,f2(x)=cosx在上单调递减,
且f2(x)=cosx∈(,1)?[0,+∞),
又y=f(x)=f1(x)+f2(x)=sinx在上单调递增,
故y=sinx是区间上的“偏增函数”.
(2)证明:①当b>0时,令f1(x)=(k+1)x,f2(x)=﹣x+b,D=(0,b),显然D=(0,b)?[0,+∞),
∵k>0,∴f(x)=kx+b在(0,b)上单调递增,
f1(x)=(k+1)x在(0,b)上单调递增,f2(x)=﹣x+b在(0,b)上单调递减,
且对任意的x∈(0,b),b>f2(x)>f2(b)=0,
因此b>0时,必存在一个区间(0,b),使f(x)=kx+b(k>0)为D上的“偏增函数.
②当b≤0时,取c>0,且满足c+b>0,令f1(x)=(k+1)x﹣c,f2(x)=﹣x+b+c,D=(0,b+c)?[0,+∞),
显然,f(x)=kx+b在(0,b+c)上单调递增,
f1(x)=(k+1)x﹣c在(0,b+c)上单调递增,f2(x)=﹣x+b+c在(0,b+c)上单调递减,
且对任意的(0,b+c),b+c>f2(x)>f2(b+c)=0,
因此b≤0时,必存在一个区间(0,b+c),使f(x)=kx+b(k>0)为D上的“偏增函数”.
综上,对任意的一次函数f(x)=kx+b(k>0),必存在一个区间D?[0,+∞),
使f(x)为D上的“偏增函数”.
点评:
本题考查函数的单调性、正余弦函数的性质,考查分类讨论思想,考查学生灵活运用知识分析问题解决新问题的能力,综合性强,难度大.
一、填空题:(本大题共14小题,每小题5分,共70分.请将答案填入答题纸填空题的相应答题线上.)
1.(5分)sin960°的值为 .
考点:
诱导公式的作用.
专题:
计算题.
分析:
利用诱导公式,先化为0°~360°的正弦,再转化为锐角的正弦,即可求得
解答:
解:由题意,sin960°=sin(720°+240°)=sin240°=sin(180°+60°)=﹣
故答案为:
点评:
本题的考点是诱导公式的应用,解题的关键是正确选用诱导公式转化.
2.(5分)函数的定义域是 (﹣∞,1) .
考点:
函数的定义域及其求法.
专题:
计算题.
分析:
根据二次根式的性质和分式的意义,被开方数大于等于0,分母不等于0,就可以求解.
解答:
解:依题意,得1﹣x>0,解得x<1,
∴函数的定义域是 (﹣∞,1)
故答案为:(﹣∞,1).
点评:
本题考查了函数自变量的取值范围:注意分式有意义,分母不为0;二次根式的被开方数是非负数.
3.(5分)已知幂函数y=f(x)的图象过点,则f(2)= 8 .
考点:
幂函数的概念、解析式、定义域、值域;函数的值.
专题:
函数的性质及应用.
分析:
设出幂函数的解析式,把点代入后求出幂指数的值,则解析式可求,从而求得f(2)的值.
解答:
解:设幂函数f(x)=xα,因为其图象过点,
所以,,解得:α=3.
所以,f(x)=x3.
则f(2)=23=8.
故答案为8.
点评:
本题考查了幂函数的概念,考查了代点求函数解析式,考查了函数值的求法,解答此题的关键是理解幂函数概念,此题是基础题.
4.(5分)若函数f(x)=x4+(m﹣1)x+1为偶函数,则实数m的值为 1 .
考点:
函数奇偶性的性质.
专题:
计算题;函数的性质及应用.
分析:
由已知可得f(﹣x)=f(x)对于任意的x都成立,代入即可求解m的值
解答:
解:∵f(x)=x4+(m﹣1)x+1为偶函数,
∴f(﹣x)=f(x)对于任意的x都成立
即(﹣x)4﹣(m﹣1)x+1=x4+(m﹣1)x+1
∴2(m﹣1)x=0对于任意x都成立
∴m=1
故答案为:1
点评:
本题主要考查了偶函数的定义的简单应用,属于基础试题
5.(5分)已知扇形的中心角为120°,半径为,则此扇形的面积为 π .
考点:
扇形面积公式.
分析:
利用扇形的面积计算公式即可得出.
解答:
解:∵弧度,∴此扇形的面积S====π.
故答案为π.
点评:
熟练掌握扇形的面积计算公式是解题的关键.
6.(5分)将函数y=sin2x的图象向右平移个单位所得函数的解析式为 y=sin(2x﹣) .
考点:
函数y=Asin(ωx+φ)的图象变换.
专题:
计算题.
分析:
左加右减上加下减的原则,直接求出将函数y=sin2x的图象向右平移个单位所得函数的解析式.
解答:
解:将函数y=sin2x的图象向右平移个单位所得函数的解析式:y=sin2(x﹣)=sin(2x﹣),
故答案为:y=sin(2x﹣).
点评:
本题主要考查三角函数的平移.三角函数的平移原则为左加右减上加下减.注意x前面的系数的应用.
7.(5分)= 6 .
考点:
对数的运算性质;有理数指数幂的化简求值.
专题:
函数的性质及应用.
分析:
利用指数幂和对数的运算性质即可得出.
解答:
解:原式=lg(4×52)+=lg102+22=2+4=6.
故答案为6.
点评:
熟练掌握指数幂和对数的运算性质是解题的关键.
8.(5分)在平面直角坐标系xoy中,已知以x轴为始边的角α、β的终边分别经过点(﹣4,3)、(3,4),则tan(α+β)= .
考点:
两角和与差的正切函数;任意角的三角函数的定义;同角三角函数间的基本关系.
专题:
三角函数的图像与性质.
分析:
由三角函数的定义可得tanα=,tanβ=,代入两角和的正切公式计算可得答案.
解答:
解:由题意结合三角函数的定义可得
tanα==,tanβ=,
由两角和的正切公式可得
tan(α+β)===,
故答案为:
点评:
本题考查三角函数的定义,以及两角和的正切公式,属基础题.
9.(5分)函数f(x)=|x+2|+x2的单调增区间是 (也对) .
考点:
函数单调性的判断与证明.
专题:
函数的性质及应用.
分析:
去掉绝对值符号把f(x)转化为分段函数,把各段中的单调区间求出来,然后即可得到答案.
解答:
解:f(x)==,
当x<﹣2时,f(x)=单调递减;
当x≥﹣2时,f(x)=在(﹣,+∞)上递增,在(﹣2,﹣)上递减,
综上知,f(x)的增区间为:(﹣,+∞).
点评:
本题考查绝对值函数单调区间的求法,该类问题常见方法为:作出图象,用图象求解;去绝对值转化为分段函数解决.
10.(5分)如图,在4×4的方格纸中,若起点和终点均在格点的向量、、满足=x+y(x,y∈R),则4x+y的值为 7 .
考点:
简单线性规划.
专题:
计算题;平面向量及应用.
分析:
将题中的4×4的方格放入如图坐标系,并设小方格边长是1,可得向量、、的坐标形式,根据=x+y建立关于x、y的方程组,解之即可得到4x+y的值.
解答:
解:作出如图直角坐标系,设方格正方形的边长为单位长度1,
可得=(1,3),=(3,﹣2),=(4,3)
∵=x+y(x,y∈R),
∴,将方程组中两式相加,可得4x+y=7
故答案为:7
点评:
本题给出4×4的方格纸中的向量量、、,在已知它们的线性关系情况下求4x+y之值,着重考查了平面向量线性运算的坐标表示的知识,属于基础题.
11.(5分)若函数f(x)=x2﹣2ax+b(a>1)的定义域与值域都是[1,a],则实数b= 5 .
考点:
函数的值域;函数的定义域及其求法.
专题:
函数的性质及应用.
分析:
首先求出函数的对称轴方程,由此判断函数在给定的定义域[1,a]内是减函数,再根据函数的值域也是[1,a],联立,可求b的值.
解答:
解:函数f(x)=x2﹣2ax+b(a>1)的对称轴方程为x=,
所以函数f(x)=x2﹣2ax+b在[1,a]上为减函数,
又函数在[1,a]上的值域也为[1,a],
则,即,
由①得:b=3a﹣1,代入②得:a2﹣3a+2=0,解得:a=1(舍),a=2.
把a=2代入b=3a﹣1得:b=5.
故答案为5.
点评:
本题考查了二次函数的单调性,考查了函数的值域的求法,考查了方程思想,解答此题的关键是判断函数在给定定义域内的单调性,此题是基础题.
12.(5分)已知直线与函数f(x)=cosx,g(x)=sin2x和h(x)=sinx的图象及x轴依次交于点P,M,N,Q,则PN2+MQ2的最小值为 .
考点:
二倍角的正弦;函数的值域;正弦函数的单调性.
分析:
正确画出三角函数的图象,进而由图象可列出式子表达已知条件,利用三角函数的单调性、有界性和二次函数的单调性即可得出最小值.
解答:
解:如图所示,
则PN2+MQ2=(cosx﹣sinx)2+sin22x=sin22x﹣sin2x+1=,
因此当时,则PN2+MQ2的最小值为.
故答案为.
点评:
熟练掌握数形结合的思想方法、三角函数的单调性、有界性和二次函数的单调性是解题的关键.
13.(5分)已知点G、H分别为△ABC的重心(三条中线的交点)、垂心(三条高所在直线的交点),若,则的值为 .
考点:
平面向量数量积的运算;三角形五心.
专题:
平面向量及应用.
分析:
利用三角形的重心和垂心的性质、向量的运算法则、数量积的定义即可得出.
解答:
解:如图所示:
设AE、AD分别为BC边上的中线、高,则,.
∴==
====﹣.
故答案为.
点评:
熟练掌握三角形的重心和垂心的性质、向量的运算法则、数量积的定义是解题的关键.
14.(5分)已知函数f(x)=mx﹣1,g(x)=x2﹣(m+1)x﹣1,若对任意的x0>0,f(x0)与g(x0)的值不异号,则实数m的值为 .
考点:
其他不等式的解法;函数单调性的性质;二次函数的性质;函数的零点.
专题:
计算题;不等式的解法及应用.
分析:
通过m大于0,等于0,小于0,分别判断对任意的x0>0,f(x0)与g(x0)的值不异号,是否成立,求出m的值即可.
解答:
解:当m=0时,不满足条件(可知(x)=mx﹣1与X Y轴都有交点)
当m>0时,画出两函数图象需满足g()=0且<得出m=;
当m<0时,因为一次函数f(x)=mx﹣1在x趋近于正无穷大时候为负无穷大,
而二次函数g(x)=x2﹣(m+1)x﹣1,在x趋近于正无穷大时为正无穷大,不满足要求.
综上:m=.
故答案为:.
点评:
本题考查一次函数与二次函数的图象的性质,函数的单调性,对称性,考查分析问题解决问题的能力.
二、解答题(本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤.)
15.(14分)已知集合A={x|2≤x≤6,x∈R},B={x|﹣1<x<5,x∈R},全集U=R.
(1)求A∩(CUB);
(2)若集合C={x|x<a,x∈R},A∩C=?,求实数a的取值范围.
考点:
交、并、补集的混合运算.
专题:
不等式的解法及应用.
分析:
(1)本题为集合的运算问题,结合数轴依据集合运算的定义即可求出集合A∩(CUB);
(2)利用数轴通过A∩C=?,直接求a的取值范围.
解答:
解:(1)∵B={x|﹣1<x<5,x∈R},
∴CUB={x|x≤﹣1或x≥5},…(4分)
∴A∩(CUB)={x|5≤x≤6}. …(8分)
(2)∵A={x|2≤x≤6,x∈R},
C={x|x<a,x∈R},A∩C=?,如图,
∴a的取值范围是a≤2. …(14分)
(不写等号扣2分)
点评:
本题考查集合的运算问题,考查数形结合思想解题,属基本运算的考查.
16.(14分)已知函数的部分图象如图所示.
(1)求A,ω的值;
(2)求f(x)的单调增区间;
(3)求f(x)在区间上的最大值和最小值.
考点:
y=Asin(ωx+φ)中参数的物理意义;正弦函数的定义域和值域;正弦函数的单调性.
专题:
计算题;三角函数的图像与性质.
分析:
(1)通过函数的图象直接求A,利用函数的周期即可求出ω的值;
(2)根据函数的单调增区间,直接求f(x)的单调增区间即可;
(3)通过x∈,求出函数的相位的范围,利用正弦函数的最值,直接求解f(x)的最大值和最小值.
解答:
解:(1)由图象知A=1,…(2分)
由图象得函数的最小正周期为,
则由得ω=2.…(4分)
(2)∵,
∴.
∴.
所以f(x)的单调递增区间为.…(9分)
(3)∵,∵,
∴.
∴.…(12分)
当,即时,f(x)取得最大值1;
当,即时,f(x)取得最小值.…(14分)
点评:
本题考查函数解析式的求法,正弦函数的单调性的应用,正弦函数的最值的求法,考查计算能力.
17.(14分)销售甲、乙两种商品所得利润分别是y1、y2万元,它们与投入资金x万元的关系分别为,y2=bx,(其中m,a,b都为常数),函数y1,y2对应的曲线C1、C2如图所示.
(1)求函数y1、y2的解析式;
(2)若该商场一共投资4万元经销甲、乙两种商品,求该商场所获利润的最大值.
考点:
根据实际问题选择函数类型;函数解析式的求解及常用方法.
专题:
函数的性质及应用.
分析:
(1)根据所给的图象知,两曲线的交点坐标为,由此列出关于m,a的方程组,解出m,a的值,即可得到函数y1、y2的解析式;
(2)对甲种商品投资x(万元),对乙种商品投资(4﹣x)(万元),根据公式可得甲、乙两种商品的总利润y(万元)关于x的函数表达式;再利用配方法确定函数的对称轴,结合函数的定义域,即可求得总利润y的最大值.
解答:
解:(1)由题意,解得,…(4分)
又由题意得(x≥0)…(7分)
(不写定义域扣一分)
(2)设销售甲商品投入资金x万元,则乙投入(4﹣x)万元
由(1)得,(0≤x≤4)…(10分)
令,则有=,,
当t=2即x=3时,y取最大值1.
答:该商场所获利润的最大值为1万元.…(14分)
(不答扣一分)
点评:
本题考查了函数模型的构建以及换元法、配方法求函数的最值,体现用数学知识解决实际问题,属于基础题.
18.(16分)已知向量=(1,cosα),=(1,sinβ),=(3,1),且(+)∥.
(1)若,求cos2β的值;
(2)证明:不存在角α,使得等式|+|=|﹣|成立;
(3)求?﹣2的最小值.
考点:
平行向量与共线向量;二次函数在闭区间上的最值.
专题:
函数的性质及应用.
分析:
(1)由题意可得当可得sinβ,由二倍角公式可得cos2β;
(2)假设成立,由数量积的运算可得,即cosα=﹣3,矛盾;
(3)由(1)可得,代入可得所求式子为关于cosα的二次函数,进而可得最值.
解答:
解:∵,=(3,1),且()∥.∴…(3分)
(1)∵,∴,∴,∴…(6分)
(2)假设存在角α使得等式成立则有
∴,∴cosα=﹣3,不成立,∴不存在角α使得等式成立.…(11分)
(3)∵∴,
∴,又﹣1≤cosα≤1,∴,…(13分)
∴当cosα=1时,. …(16分)
点评:
本题考查平行向量,以及二次函数在闭区间的最值,属基础题.
19.(16分)已知函数f(x)=x2,g(x)=ax+3(a∈R).
(1)记函数F(x)=f(x)﹣g(x),
(i)判断函数F(x)的零点个数;
(ii)若函数|F(x)|在[0,1]上是减函数,求实数a的取值范围.
(2)设.若对于函数y=G(x)图象上异于原点O的任意一点P,在函数y=G(x)图象上总存在另一点Q,使得,且PQ的中点在y轴上,求a的取值范围.
考点:
平面向量数量积的运算;函数单调性的判断与证明;根的存在性及根的个数判断.
专题:
计算题;函数的性质及应用;平面向量及应用.
分析:
(1)利用函数F(x)=f(x)﹣g(x)求出表达式,
(i)利用判别式的符号,直接判断函数F(x)的零点个数;
(ii)通过函数|F(x)|在[0,1]上是减函数,化简函数的表达式,利用函数的对称轴,以及1处的函数值,列出不等式组,求实数a的取值范围.
(2)通过.求出函数y=G(x)的表达式,设出点P的坐标、Q的坐标,通过,且PQ的中点在y轴上,求出a的取值范围.
解答:
解:(1)(i)F(x)=x2﹣ax﹣3
∵∴函数F(x)有2个零点. …(4分)
(ii) ,当a≤0时,图象为:
当a>0时,图象为:
由题意.解得﹣2≤a≤0…(8分)
(2),
由题意易知P,Q两点在y轴的两侧,不妨设P点坐标在y轴的左侧,设,
当﹣1<x1<0,则,恒成立,…(12分)
当x1≤﹣1,则设点Q(﹣x1,﹣ax1+3),恒成立,
∴ax1>2恒成立,∵x1≤﹣1,
∴恒成立,只要∴,…(14分)
∵x1≤﹣1,∴,
∴a<﹣2. …(16分)
点评:
本题考查函数的零点,函数与方程的关系的应用,恒成立问题的应用,平面向量的数量积的应用,考查分析问题解决问题的能力.
20.(16分)已知函数f(x)是区间D?[0,+∞)上的增函数,若f(x)可表示为f(x)=f1(x)+f2(x),且满足下列条件:①f1(x)是D上的增函数;②f2(x)是D上的减函数;③函数f2(x)的值域A?[0,+∞),则称函数f(x)是区间D上的“偏增函数”.
(1)(i) 问函数y=sinx+cosx是否是区间上的“偏增函数”?并说明理由;
(ii)证明函数y=sinx是区间上的“偏增函数”.
(2)证明:对任意的一次函数f(x)=kx+b(k>0),必存在一个区间D?[0,+∞),使f(x)为D上的“偏增函数”.
考点:
奇偶性与单调性的综合.
专题:
新定义;函数的性质及应用.
分析:
(1)(i)记f1(x)=sinx,f2(x)=cosx,根据偏增函数的定义及正余弦函数的性质可作出判断;(ii)f(x)=(sinx﹣cosx)+cosx,记,根据偏增函数的定义可证明;
(2)分情况讨论:①当b>0时,令f1(x)=(k+1)x,f2(x)=﹣x+b,取D=(0,b);②当b≤0时,取c>0,且满足c+b>0,令f1(x)=(k+1)x﹣c,f2(x)=﹣x+b+c,D=(0,b+c),根据偏增函数定义即可证明;
解答:
(1)解:(i) y=sinx+cosx是区间上的“偏增函数”.
记f1(x)=sinx,f2(x)=cosx,显然f1(x)=sinx在上单调递增,f2(x)=cosx在上单调递减,
且f2(x)=cosx∈(,1)?[0,+∞),
又在上单调递增,
故y=sinx+cosx是区间上的“偏增函数”.
(ii)证明:,
记,
显然在上单调递增,f2(x)=cosx在上单调递减,
且f2(x)=cosx∈(,1)?[0,+∞),
又y=f(x)=f1(x)+f2(x)=sinx在上单调递增,
故y=sinx是区间上的“偏增函数”.
(2)证明:①当b>0时,令f1(x)=(k+1)x,f2(x)=﹣x+b,D=(0,b),显然D=(0,b)?[0,+∞),
∵k>0,∴f(x)=kx+b在(0,b)上单调递增,
f1(x)=(k+1)x在(0,b)上单调递增,f2(x)=﹣x+b在(0,b)上单调递减,
且对任意的x∈(0,b),b>f2(x)>f2(b)=0,
因此b>0时,必存在一个区间(0,b),使f(x)=kx+b(k>0)为D上的“偏增函数.
②当b≤0时,取c>0,且满足c+b>0,令f1(x)=(k+1)x﹣c,f2(x)=﹣x+b+c,D=(0,b+c)?[0,+∞),
显然,f(x)=kx+b在(0,b+c)上单调递增,
f1(x)=(k+1)x﹣c在(0,b+c)上单调递增,f2(x)=﹣x+b+c在(0,b+c)上单调递减,
且对任意的(0,b+c),b+c>f2(x)>f2(b+c)=0,
因此b≤0时,必存在一个区间(0,b+c),使f(x)=kx+b(k>0)为D上的“偏增函数”.
综上,对任意的一次函数f(x)=kx+b(k>0),必存在一个区间D?[0,+∞),
使f(x)为D上的“偏增函数”.
点评:
本题考查函数的单调性、正余弦函数的性质,考查分类讨论思想,考查学生灵活运用知识分析问题解决新问题的能力,综合性强,难度大.
同课章节目录
