行程问题(课件)六年级下册数学人教版(共19张PPT)
文档属性
| 名称 | 行程问题(课件)六年级下册数学人教版(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 189.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-29 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
行程问题
六年级数学专题复习
1.甲、乙两人骑车同时从东、西两地相向而行,8小时相遇。如果甲每小时少行1千米,乙每小时多行3千米,这样过7小时就可以相遇。东西两地相距多少千米?
8小时
7小时
表示原来速度和
解:现在速度和比原来速度和快3-1=2(千米)
原来速度和:2 × 7=14(千米/小时)
东西两地相距:14 × 8=112(千米)
答:东西两地相距112千米。
表示现在速度和
2.甲、乙两车同时从东西两地相对开出,6小时相遇。如果甲车每小时少行9千米,乙车每小时多行6千米,那么经过6小时后,两车已行路程是剩下路程的19倍。东、西两地相距多少千米?
解:现在速度和比原来速度和慢9-6=3(千米)
经过6小时后剩余路程:3× 6=18(千米/小时)
东西两地相距:18×20=360(千米)
答:东西两地相距360千米。
思路分析:甲乙 第二次相遇时,甲乙共走了
三个全程:21×3=63(千米)此时,甲走到
路程比乙走的多9千米。第二次相遇时,
乙走的路程是:(63-9)÷2=27(千米)
甲走的路程是:27+9=36(千米)
甲的速度是:36÷(10-8)=18(千米)
答:甲一共行了36千米,每小时走18千。
3.A、B两地相距21千米。上午8时甲、乙两人分别从A、B两地同时出发,相向而行。甲到达B地后立即返回,乙到达A地后立即返回。上午10时他们第二次相遇,此时,甲走到路程比乙走的多9千米。甲一共行了多少千米?甲每小时走多少千米?
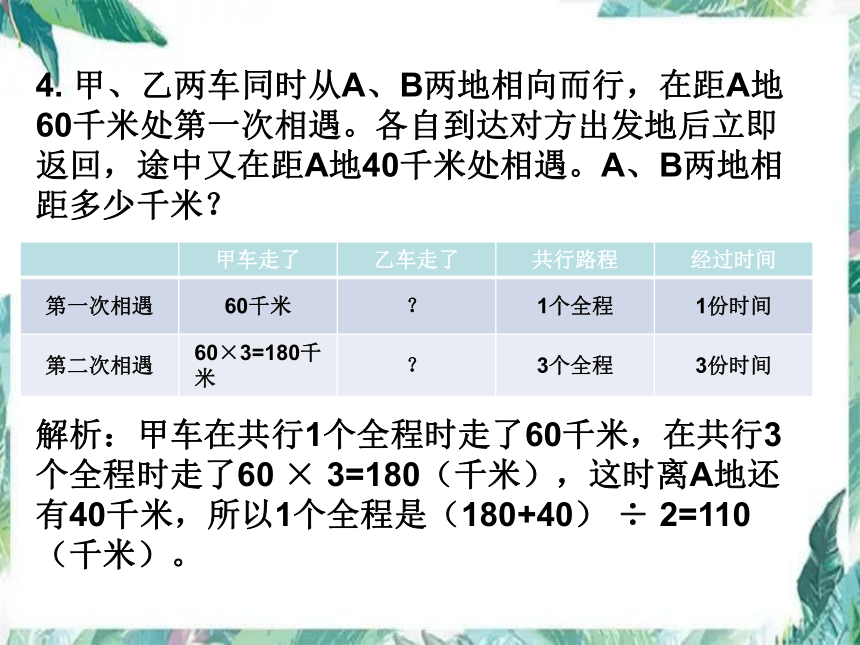
4. 甲、乙两车同时从A、B两地相向而行,在距A地60千米处第一次相遇。各自到达对方出发地后立即返回,途中又在距A地40千米处相遇。A、B两地相距多少千米?
甲车走了 乙车走了 共行路程 经过时间
第一次相遇 60千米 ? 1个全程 1份时间
第二次相遇 60×3=180千米 ? 3个全程 3份时间
解析:甲车在共行1个全程时走了60千米,在共行3个全程时走了60 × 3=180(千米),这时离A地还有40千米,所以1个全程是(180+40) ÷ 2=110(千米)。
解:由题意知,乙车48分钟行了24千米。
解法一:乙车的速度:24÷48×60=30(千米/小时)
甲行完全程用的时间165÷30-(48÷60)=4.7(小时)
解法二:算一下165千米中含有几个24千米,得出乙车行完全程所用的时间:165÷24×48=330(分钟)
甲车行完全程所用的时间(330-48)÷60=4.7(小时)
答:甲车行完全程用了4.7小时。
5.甲、乙两辆汽车同时从某地出发,发送一批货物到距离165千米的工地。甲比乙车早到48分钟,当甲车到达时,乙车还距工地24千米。甲车行完全程用了多少个小时?
6.客车从甲地开往乙地,货车从乙地开往甲地,同时开出,到达对方出发地后立即返回。第一次相遇距乙地80千米,第二次相遇距甲地50千米。甲、乙两地相距多少千米?
解析:货车在共行1个全程中走了80千米,3个全程中走了80 ×3=240(千米),
到了第二次相遇点去掉50千米就是全程240-50=190(千米)。
7.小明早上从家中去学校,以每分钟6米的速度前进,10分钟后,爸爸发现小明的书包忘在家里了,随后以每分钟10米的速度向前去追小明,多长时间后爸爸能追上小明?
解:爸爸追之前,小明已经走6×10=60(米),
即追及路程为60米,而爸爸每分钟可追:10-6=4(米)
则所需时间为60÷4=15(分钟)
答:15分钟后爸爸可以追上小明。
解:由题意可知:
第一次相遇时,甲乙行完了一个全程,甲行了60千米;
第二次相遇时,甲乙行完了三个全程,推算出甲行了3个60 千米。可知如果甲再行30千米,甲行的路程是全程的1.5倍。
(60×3+30)÷1.5=140(千米)
答:两站相距140千米。
8.甲乙两辆汽车同时从东、西两站相向出发。第一次在离东站60千米的地方相遇。之后,两车继续以原来的速度前进。各自到达对方的车站后都立即返回。又在距中点西侧30千米出相遇。两站相距多少千米?
9.甲乙两车同时从AB两地相向而行,4小时后甲车行全程的 ,乙行的路程超过中点13千米,已知甲车比乙车每小时快3千米,AB两地相距多少千米?
A
B
乙行全程的
多13千米
甲行全程
乙行全程的
多13千米
3×4=12km
(13+3×4)÷( - )
用比例解行程问题三量关系:
运动时间相同:S甲:S乙= V甲:V乙
(路程和速度成正比)
运动速度相同:S甲:S乙= T甲:T乙
运动路程相同: V甲:V乙= T乙:T甲
(速度与时间成反比)
(二)行程问题与比例的结合:
行 程 问 题
不变速问题
变速问题
例1:路程相同
例2:时间相同
例3例4:时间相同的变形
例5:单变速
例6:双变速
例7:分段变速
1.一辆汽车从甲地开往乙地,去时每小时行48千米,返回时每小时行56千米,返回比去时少用1小时。求甲乙两地相距多少千米?
V去:V回=48:56=6:7
∵路程相同 ∴T去:T回=7:6
去时时间:1÷(7-6)×7=7(小时)
甲乙相距路程:48×7=336(千米)
答:甲乙两地相距336千米。
运动路程相同: V甲:V乙= T乙:T甲
运动时间相同:V甲:V乙= S甲:S乙
A
B
V甲:V乙=48:56=6:7
∵时间相同 ∴S甲:S乙=6:7
乙行全程
7份
6份
甲行全程
24千米
2.甲乙两车分别从A、B两地同时出发,相向而行,甲每小时行48千米,乙每小时行56千米,当乙车行至全程 时,甲距中点还有24千米 。求A、B两地相距多少千米?
甲到达终点时:
S乙:S丙=(100-8):(100-12)=23:22
3.甲、乙、丙三人进行百米赛跑,当甲到达终点时,乙距终点8米,丙距终点12米,当乙到终点时,丙距终点多少米?
丙
甲
乙
12米
8米
?米
乙到达终点时,丙距终点:
12-8÷23×22= (米)
答:丙距终点 米
4.甲、乙二人同时从A到B地,当甲行全程的40﹪,乙距B地还有150千米;当甲到B地,乙距B地的路程与甲所行的路程比是3:8,求A、B两地相距多少千米?
A
B
40﹪
150千米
S甲:S乙=
8份
5份
40﹪÷8×5份
150÷(1- 40﹪÷8×5)
150千米
5.甲、乙两车同时从A、B两地相向开出,甲、乙两车速度比是5:4,两车相遇后,乙车每小时比原来多行18千米,结果两车恰好同时到达对方出发地,甲车每小时行多少千米?
分析:(1)乙速变化,甲速不变。甲速是不变量。
相遇时:
V甲:V乙=5:4
S甲:S乙=5:4
甲
乙
5
4
从相遇到对方出发地:
S甲:S乙=4:5
4
5
V甲:V后乙=4:5
A
B
V甲:V乙=5:4
V甲:V后乙=4:5
= 20:16
= 20:25
18÷(25-16)×20
=18 ÷9 ×20
=400(千米)
答:甲车每小时行400千米。
6.甲、乙两车同时从A、B两地相向开出,甲、乙两车速度比是5:4,两车相遇后,甲的速度减少20﹪,乙速增加20﹪,当甲到达B地时,乙离A地还有10千米,那么A、B两地相距多少千米?
A
B
甲
乙
5
4
10千米
相遇时:V甲:V乙=5:4
S甲:S乙=5:4
相遇后:V甲:V乙=5×(1-20﹪):4 ×(1-20﹪)=5:6
4
10÷(5- 4÷5×6) ×(5+4)=450(千米)
4÷5×6
5-4÷5×6
答: A、B两地相距450千米。
行程问题
六年级数学专题复习
1.甲、乙两人骑车同时从东、西两地相向而行,8小时相遇。如果甲每小时少行1千米,乙每小时多行3千米,这样过7小时就可以相遇。东西两地相距多少千米?
8小时
7小时
表示原来速度和
解:现在速度和比原来速度和快3-1=2(千米)
原来速度和:2 × 7=14(千米/小时)
东西两地相距:14 × 8=112(千米)
答:东西两地相距112千米。
表示现在速度和
2.甲、乙两车同时从东西两地相对开出,6小时相遇。如果甲车每小时少行9千米,乙车每小时多行6千米,那么经过6小时后,两车已行路程是剩下路程的19倍。东、西两地相距多少千米?
解:现在速度和比原来速度和慢9-6=3(千米)
经过6小时后剩余路程:3× 6=18(千米/小时)
东西两地相距:18×20=360(千米)
答:东西两地相距360千米。
思路分析:甲乙 第二次相遇时,甲乙共走了
三个全程:21×3=63(千米)此时,甲走到
路程比乙走的多9千米。第二次相遇时,
乙走的路程是:(63-9)÷2=27(千米)
甲走的路程是:27+9=36(千米)
甲的速度是:36÷(10-8)=18(千米)
答:甲一共行了36千米,每小时走18千。
3.A、B两地相距21千米。上午8时甲、乙两人分别从A、B两地同时出发,相向而行。甲到达B地后立即返回,乙到达A地后立即返回。上午10时他们第二次相遇,此时,甲走到路程比乙走的多9千米。甲一共行了多少千米?甲每小时走多少千米?
4. 甲、乙两车同时从A、B两地相向而行,在距A地60千米处第一次相遇。各自到达对方出发地后立即返回,途中又在距A地40千米处相遇。A、B两地相距多少千米?
甲车走了 乙车走了 共行路程 经过时间
第一次相遇 60千米 ? 1个全程 1份时间
第二次相遇 60×3=180千米 ? 3个全程 3份时间
解析:甲车在共行1个全程时走了60千米,在共行3个全程时走了60 × 3=180(千米),这时离A地还有40千米,所以1个全程是(180+40) ÷ 2=110(千米)。
解:由题意知,乙车48分钟行了24千米。
解法一:乙车的速度:24÷48×60=30(千米/小时)
甲行完全程用的时间165÷30-(48÷60)=4.7(小时)
解法二:算一下165千米中含有几个24千米,得出乙车行完全程所用的时间:165÷24×48=330(分钟)
甲车行完全程所用的时间(330-48)÷60=4.7(小时)
答:甲车行完全程用了4.7小时。
5.甲、乙两辆汽车同时从某地出发,发送一批货物到距离165千米的工地。甲比乙车早到48分钟,当甲车到达时,乙车还距工地24千米。甲车行完全程用了多少个小时?
6.客车从甲地开往乙地,货车从乙地开往甲地,同时开出,到达对方出发地后立即返回。第一次相遇距乙地80千米,第二次相遇距甲地50千米。甲、乙两地相距多少千米?
解析:货车在共行1个全程中走了80千米,3个全程中走了80 ×3=240(千米),
到了第二次相遇点去掉50千米就是全程240-50=190(千米)。
7.小明早上从家中去学校,以每分钟6米的速度前进,10分钟后,爸爸发现小明的书包忘在家里了,随后以每分钟10米的速度向前去追小明,多长时间后爸爸能追上小明?
解:爸爸追之前,小明已经走6×10=60(米),
即追及路程为60米,而爸爸每分钟可追:10-6=4(米)
则所需时间为60÷4=15(分钟)
答:15分钟后爸爸可以追上小明。
解:由题意可知:
第一次相遇时,甲乙行完了一个全程,甲行了60千米;
第二次相遇时,甲乙行完了三个全程,推算出甲行了3个60 千米。可知如果甲再行30千米,甲行的路程是全程的1.5倍。
(60×3+30)÷1.5=140(千米)
答:两站相距140千米。
8.甲乙两辆汽车同时从东、西两站相向出发。第一次在离东站60千米的地方相遇。之后,两车继续以原来的速度前进。各自到达对方的车站后都立即返回。又在距中点西侧30千米出相遇。两站相距多少千米?
9.甲乙两车同时从AB两地相向而行,4小时后甲车行全程的 ,乙行的路程超过中点13千米,已知甲车比乙车每小时快3千米,AB两地相距多少千米?
A
B
乙行全程的
多13千米
甲行全程
乙行全程的
多13千米
3×4=12km
(13+3×4)÷( - )
用比例解行程问题三量关系:
运动时间相同:S甲:S乙= V甲:V乙
(路程和速度成正比)
运动速度相同:S甲:S乙= T甲:T乙
运动路程相同: V甲:V乙= T乙:T甲
(速度与时间成反比)
(二)行程问题与比例的结合:
行 程 问 题
不变速问题
变速问题
例1:路程相同
例2:时间相同
例3例4:时间相同的变形
例5:单变速
例6:双变速
例7:分段变速
1.一辆汽车从甲地开往乙地,去时每小时行48千米,返回时每小时行56千米,返回比去时少用1小时。求甲乙两地相距多少千米?
V去:V回=48:56=6:7
∵路程相同 ∴T去:T回=7:6
去时时间:1÷(7-6)×7=7(小时)
甲乙相距路程:48×7=336(千米)
答:甲乙两地相距336千米。
运动路程相同: V甲:V乙= T乙:T甲
运动时间相同:V甲:V乙= S甲:S乙
A
B
V甲:V乙=48:56=6:7
∵时间相同 ∴S甲:S乙=6:7
乙行全程
7份
6份
甲行全程
24千米
2.甲乙两车分别从A、B两地同时出发,相向而行,甲每小时行48千米,乙每小时行56千米,当乙车行至全程 时,甲距中点还有24千米 。求A、B两地相距多少千米?
甲到达终点时:
S乙:S丙=(100-8):(100-12)=23:22
3.甲、乙、丙三人进行百米赛跑,当甲到达终点时,乙距终点8米,丙距终点12米,当乙到终点时,丙距终点多少米?
丙
甲
乙
12米
8米
?米
乙到达终点时,丙距终点:
12-8÷23×22= (米)
答:丙距终点 米
4.甲、乙二人同时从A到B地,当甲行全程的40﹪,乙距B地还有150千米;当甲到B地,乙距B地的路程与甲所行的路程比是3:8,求A、B两地相距多少千米?
A
B
40﹪
150千米
S甲:S乙=
8份
5份
40﹪÷8×5份
150÷(1- 40﹪÷8×5)
150千米
5.甲、乙两车同时从A、B两地相向开出,甲、乙两车速度比是5:4,两车相遇后,乙车每小时比原来多行18千米,结果两车恰好同时到达对方出发地,甲车每小时行多少千米?
分析:(1)乙速变化,甲速不变。甲速是不变量。
相遇时:
V甲:V乙=5:4
S甲:S乙=5:4
甲
乙
5
4
从相遇到对方出发地:
S甲:S乙=4:5
4
5
V甲:V后乙=4:5
A
B
V甲:V乙=5:4
V甲:V后乙=4:5
= 20:16
= 20:25
18÷(25-16)×20
=18 ÷9 ×20
=400(千米)
答:甲车每小时行400千米。
6.甲、乙两车同时从A、B两地相向开出,甲、乙两车速度比是5:4,两车相遇后,甲的速度减少20﹪,乙速增加20﹪,当甲到达B地时,乙离A地还有10千米,那么A、B两地相距多少千米?
A
B
甲
乙
5
4
10千米
相遇时:V甲:V乙=5:4
S甲:S乙=5:4
相遇后:V甲:V乙=5×(1-20﹪):4 ×(1-20﹪)=5:6
4
10÷(5- 4÷5×6) ×(5+4)=450(千米)
4÷5×6
5-4÷5×6
答: A、B两地相距450千米。
