4.4 图形变化的简单应用同步练习(含答案)
文档属性
| 名称 | 4.4 图形变化的简单应用同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-07 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第四章 图形的平移与旋转
4 图形变化的简单应用
基础过关
知识点1 图形之间的变化类型
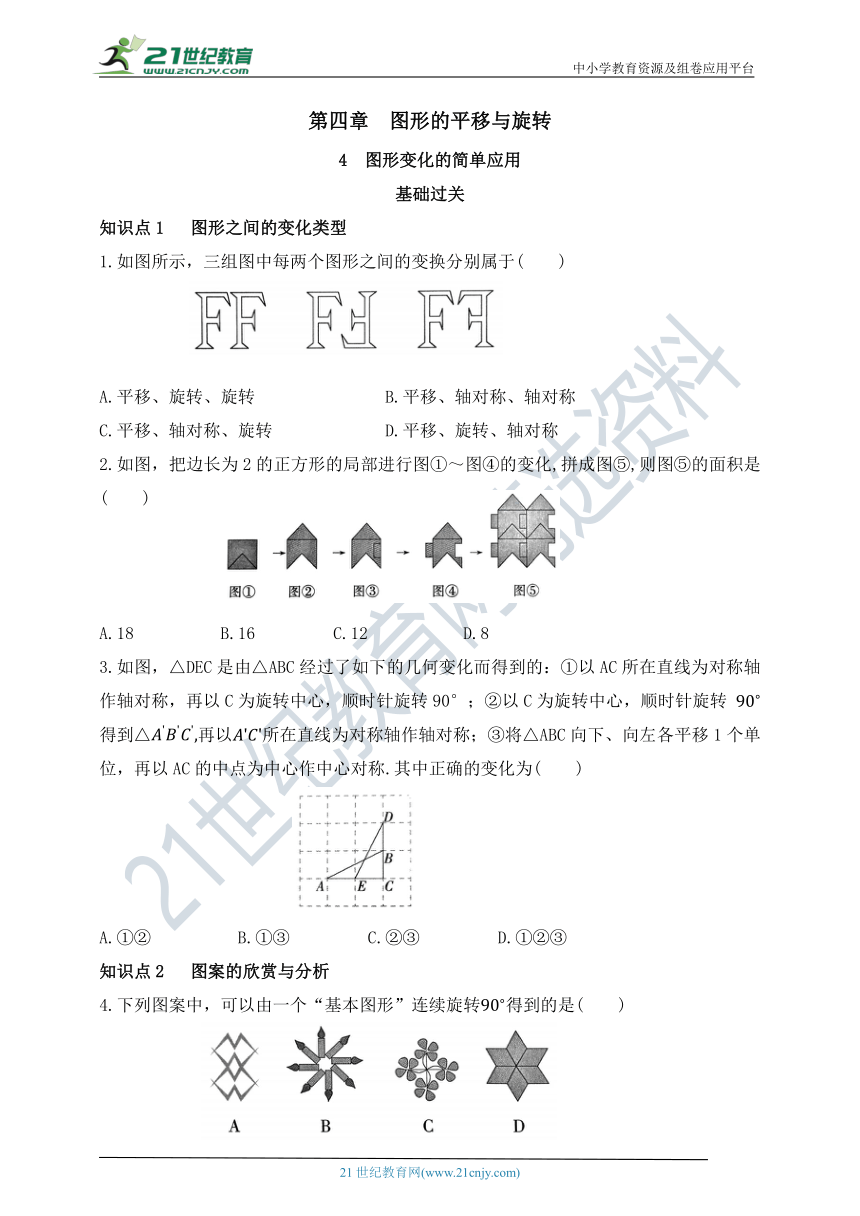
1.如图所示,三组图中每两个图形之间的变换分别属于( )
A.平移、旋转、旋转 B.平移、轴对称、轴对称
C.平移、轴对称、旋转 D.平移、旋转、轴对称
2.如图,把边长为2的正方形的局部进行图①~图④的变化,拼成图⑤,则图⑤的面积是 ( )
A.18 B.16 C.12 D.8
3.如图,△DEC是由△ABC经过了如下的几何变化而得到的:①以AC所在直线为对称轴作轴对称,再以C为旋转中心,顺时针旋转90°;②以C为旋转中心,顺时针旋转 得到△再以所在直线为对称轴作轴对称;③将△ABC向下、向左各平移1个单位,再以AC的中点为中心作中心对称.其中正确的变化为( )
A.①② B.①③ C.②③ D.①②③
知识点2 图案的欣赏与分析
4.下列图案中,可以由一个“基本图形”连续旋转得到的是( )
5.下列四个图案中,既可用旋转来分析整个图案的形成过程,又可用平移来分析整个图案的形成过程的是( )
6.利用图形的旋转可以设计出许多美丽的图案.图②中的图案是由图①中的基本图形以点O为旋转中心,顺时针(或逆时针)旋转一个角度α,依次旋转而组成的,则旋转角α的度数不可能是( )
知识点3 图案设计的步骤
7.如图,已知△
(1)以△为基本图形,借助旋转、平移或轴对称在图1中设计一个图案,使它是中心对称图形,但不是轴对称图形;
(2)以△为基本图形,借助旋转、平移或轴对称在图2中设计一个图案,使它既是轴对称图形又是中心对称图形.
能力提升
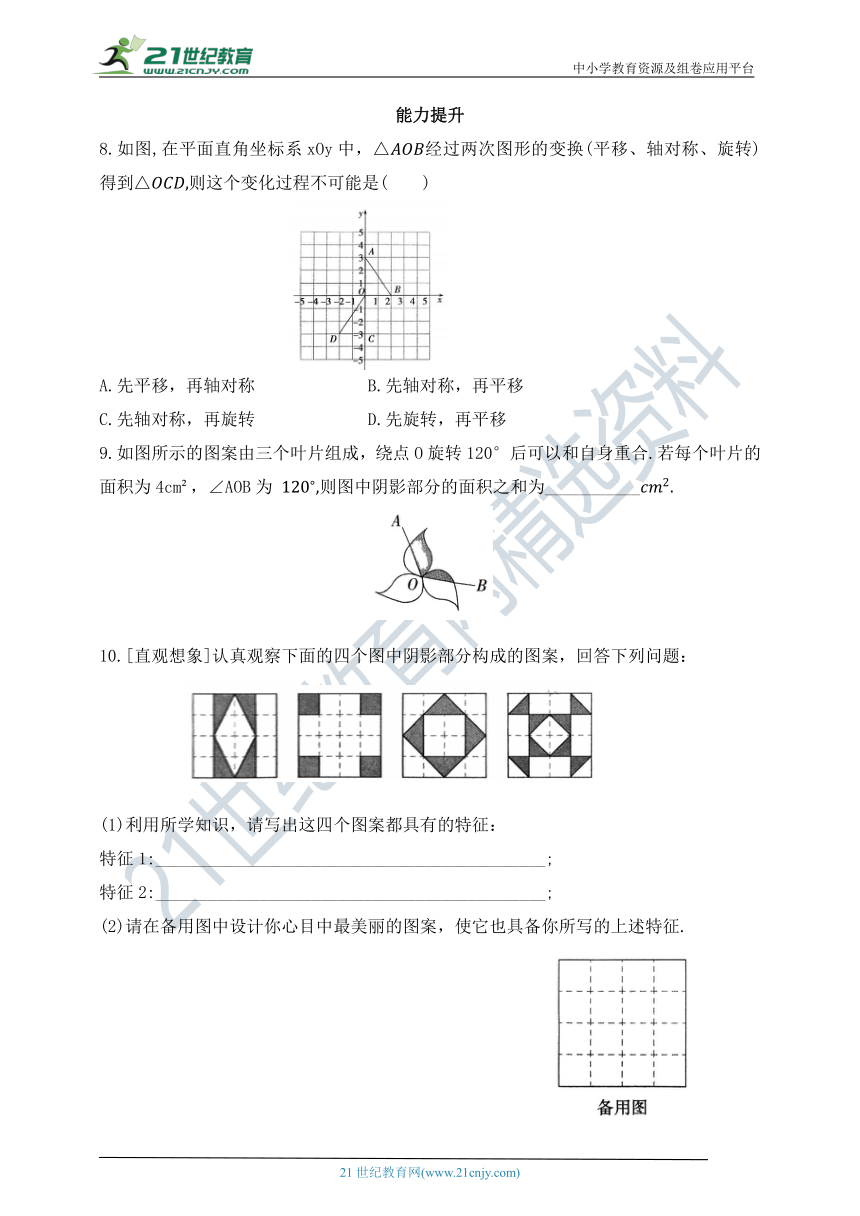
8.如图,在平面直角坐标系xOy中,△经过两次图形的变换(平移、轴对称、旋转)得到△则这个变化过程不可能是( )
A.先平移,再轴对称 B.先轴对称,再平移
C.先轴对称,再旋转 D.先旋转,再平移
9.如图所示的图案由三个叶片组成,绕点O旋转120°后可以和自身重合.若每个叶片的面积为4cm ,∠AOB为 则图中阴影部分的面积之和为___________
10.[直观想象]认真观察下面的四个图中阴影部分构成的图案,回答下列问题:
(1)利用所学知识,请写出这四个图案都具有的特征:
特征1:_____________________________________________;
特征2:_____________________________________________;
(2)请在备用图中设计你心目中最美丽的图案,使它也具备你所写的上述特征.
参考答案
基础过关
1.D 第一组可沿水平线平移得到;第二组可绕对应点连线的中点旋转得到;第三组可沿对应点连线的垂直平分线翻折得到,即轴对称.故选D.
2.B 从题图①~题图④的变化中我们发现,图形的面积没有发生变化,还是4,因为题图⑤是由4个题图④拼成的,所以题图⑤的面积是16.故选B.
3.A 易知①②满足题意,将 向下、向左各平移1个单位,所得三角形与 成轴对称,而不成中心对称,故③不符合题意.故选A.
4.C A.不能由“基本图形”连续旋转 得到,A不符合题意;B.能由“基本图形”连续旋转 得到,B不符合题意;C.能由“基本图形”连续旋转 得到,C符合题
意;D.能由“基本图形”连续旋转 得到,D不符合题意.故选C.
5.C 四个选项中的图形都可以看成是由图形的一半旋转 得到的.若一个图形可以通过某个基本图形平移得到,则这个图形可以分成几个相同的基本图形,且基本图形之间对应点的连线平行(或在同一条直线上),故A、B、D项中图形不能由平移得到,C选项中的图形可看成是由基本图形 平移得到的,故选C.
故旋转角α的度数是 的整数倍即可,结合选项可知,旋转角α的度数不可能是 故选A.
7.解析 (1)答案不唯一,如图所示,由这两个三角形组成的图案是中心对称图形,但不是轴对称图形.
(2)答案不唯一,如图所示,由这四个三角形组成的图案既是轴对称图形,又是中心对称图形.
能力提升
8.D A项,先向下平移3个单位,再沿y轴翻折,可得△COD.B项,先沿y轴翻折,再向下平移3个单位,可得△COD.C项,先沿x轴翻折,再绕(0,-1.5)旋转180°,可得△COD.D项,先旋转,再平移,不可能得到△COD,故选D.
9.答案 4
解析 ∵题图中的图案由三个叶片组成,绕点O旋转120°后可以和自身重合, 为 ∴题图中阴影部分的面积之和 故答案为4.
10.解析(1)答案不唯一,如:特征1:都是轴对称图形.
特征2:阴影部分的面积都相等.
(2)如图所示(答案不唯一).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第四章 图形的平移与旋转
4 图形变化的简单应用
基础过关
知识点1 图形之间的变化类型
1.如图所示,三组图中每两个图形之间的变换分别属于( )
A.平移、旋转、旋转 B.平移、轴对称、轴对称
C.平移、轴对称、旋转 D.平移、旋转、轴对称
2.如图,把边长为2的正方形的局部进行图①~图④的变化,拼成图⑤,则图⑤的面积是 ( )
A.18 B.16 C.12 D.8
3.如图,△DEC是由△ABC经过了如下的几何变化而得到的:①以AC所在直线为对称轴作轴对称,再以C为旋转中心,顺时针旋转90°;②以C为旋转中心,顺时针旋转 得到△再以所在直线为对称轴作轴对称;③将△ABC向下、向左各平移1个单位,再以AC的中点为中心作中心对称.其中正确的变化为( )
A.①② B.①③ C.②③ D.①②③
知识点2 图案的欣赏与分析
4.下列图案中,可以由一个“基本图形”连续旋转得到的是( )
5.下列四个图案中,既可用旋转来分析整个图案的形成过程,又可用平移来分析整个图案的形成过程的是( )
6.利用图形的旋转可以设计出许多美丽的图案.图②中的图案是由图①中的基本图形以点O为旋转中心,顺时针(或逆时针)旋转一个角度α,依次旋转而组成的,则旋转角α的度数不可能是( )
知识点3 图案设计的步骤
7.如图,已知△
(1)以△为基本图形,借助旋转、平移或轴对称在图1中设计一个图案,使它是中心对称图形,但不是轴对称图形;
(2)以△为基本图形,借助旋转、平移或轴对称在图2中设计一个图案,使它既是轴对称图形又是中心对称图形.
能力提升
8.如图,在平面直角坐标系xOy中,△经过两次图形的变换(平移、轴对称、旋转)得到△则这个变化过程不可能是( )
A.先平移,再轴对称 B.先轴对称,再平移
C.先轴对称,再旋转 D.先旋转,再平移
9.如图所示的图案由三个叶片组成,绕点O旋转120°后可以和自身重合.若每个叶片的面积为4cm ,∠AOB为 则图中阴影部分的面积之和为___________
10.[直观想象]认真观察下面的四个图中阴影部分构成的图案,回答下列问题:
(1)利用所学知识,请写出这四个图案都具有的特征:
特征1:_____________________________________________;
特征2:_____________________________________________;
(2)请在备用图中设计你心目中最美丽的图案,使它也具备你所写的上述特征.
参考答案
基础过关
1.D 第一组可沿水平线平移得到;第二组可绕对应点连线的中点旋转得到;第三组可沿对应点连线的垂直平分线翻折得到,即轴对称.故选D.
2.B 从题图①~题图④的变化中我们发现,图形的面积没有发生变化,还是4,因为题图⑤是由4个题图④拼成的,所以题图⑤的面积是16.故选B.
3.A 易知①②满足题意,将 向下、向左各平移1个单位,所得三角形与 成轴对称,而不成中心对称,故③不符合题意.故选A.
4.C A.不能由“基本图形”连续旋转 得到,A不符合题意;B.能由“基本图形”连续旋转 得到,B不符合题意;C.能由“基本图形”连续旋转 得到,C符合题
意;D.能由“基本图形”连续旋转 得到,D不符合题意.故选C.
5.C 四个选项中的图形都可以看成是由图形的一半旋转 得到的.若一个图形可以通过某个基本图形平移得到,则这个图形可以分成几个相同的基本图形,且基本图形之间对应点的连线平行(或在同一条直线上),故A、B、D项中图形不能由平移得到,C选项中的图形可看成是由基本图形 平移得到的,故选C.
故旋转角α的度数是 的整数倍即可,结合选项可知,旋转角α的度数不可能是 故选A.
7.解析 (1)答案不唯一,如图所示,由这两个三角形组成的图案是中心对称图形,但不是轴对称图形.
(2)答案不唯一,如图所示,由这四个三角形组成的图案既是轴对称图形,又是中心对称图形.
能力提升
8.D A项,先向下平移3个单位,再沿y轴翻折,可得△COD.B项,先沿y轴翻折,再向下平移3个单位,可得△COD.C项,先沿x轴翻折,再绕(0,-1.5)旋转180°,可得△COD.D项,先旋转,再平移,不可能得到△COD,故选D.
9.答案 4
解析 ∵题图中的图案由三个叶片组成,绕点O旋转120°后可以和自身重合, 为 ∴题图中阴影部分的面积之和 故答案为4.
10.解析(1)答案不唯一,如:特征1:都是轴对称图形.
特征2:阴影部分的面积都相等.
(2)如图所示(答案不唯一).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
