第四章 图形的平移与旋转综合测试题(含答案)
文档属性
| 名称 | 第四章 图形的平移与旋转综合测试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 9.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-07 15:45:12 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第四章综合测试题
(满分:100分 时间:60分钟)
一、选择题(每小题3分,共30分)
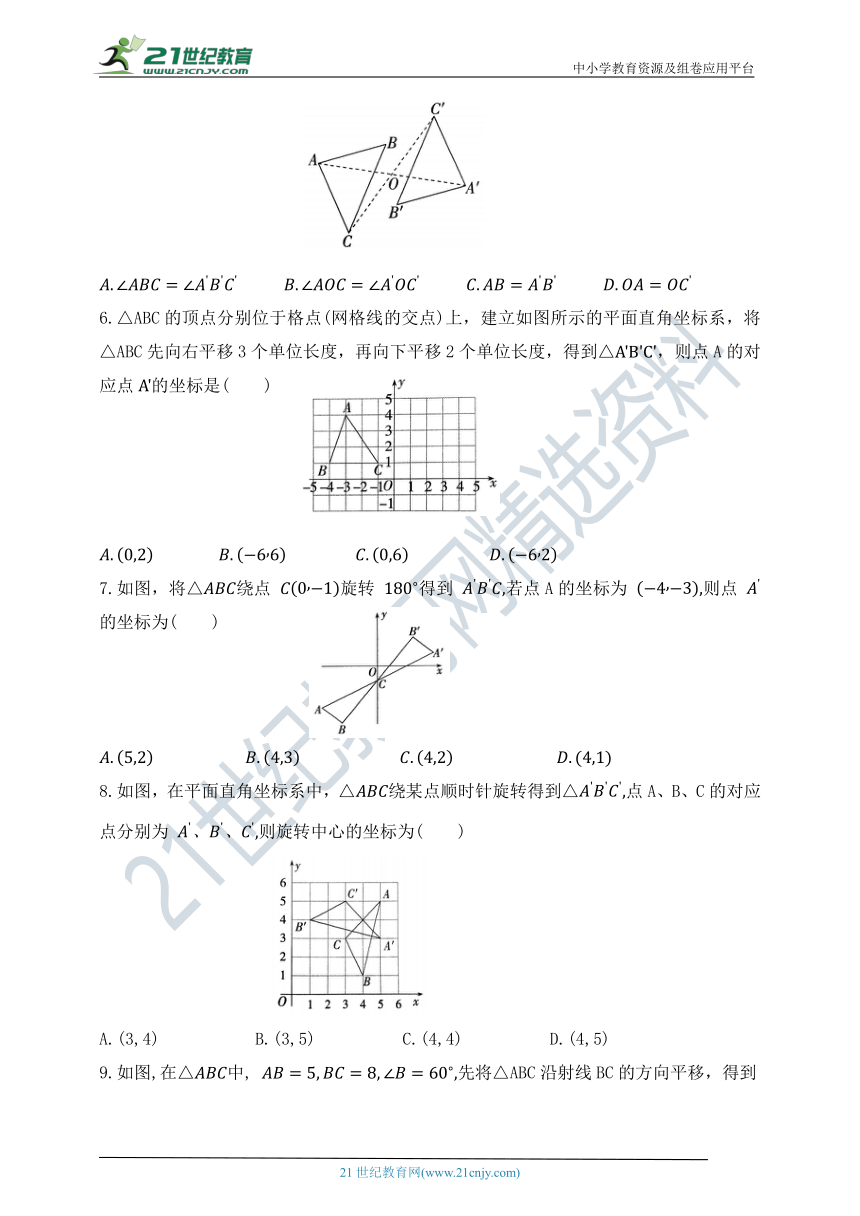
1.下列APP图标中,是中心对称图形的是( )
2.如图,在方格纸中,将Rt△AOB绕点B按顺时针方向旋转 后得到,则下列四个选项中正确的是( )
3.经过下列变换,不能由图①所示的基本图形得到图②的是( )
A.旋转 B.中心对称和轴对称 C.平移和轴对称 D.中心对称
4.如图,在三角形ABC中, 将三角形ABC沿射线BC的方向平移2.5cm后得到三角形DEF,连接AE,AD,有以下结论:①AC∥DF;②AD∥CF; ④DE⊥AC.其中结论正确的有( )
A.1个 B.2个 C.3个 D.4个
5.如图所示,已知△和△关于点O成中心对称,则下列结论不一定正确的是( )
6.△ABC的顶点分别位于格点(网格线的交点)上,建立如图所示的平面直角坐标系,将△ABC先向右平移3个单位长度,再向下平移2个单位长度,得到△,则点A的对应点的坐标是( )
7.如图,将△绕点 旋转 得到 若点A的坐标为 则点 的坐标为( )
8.如图,在平面直角坐标系中,△绕某点顺时针旋转得到△点A、B、C的对应点分别为 则旋转中心的坐标为( )
A.(3,4) B.(3,5) C.(4,4) D.(4,5)
9.如图,在△中, 先将△ABC沿射线BC的方向平移,得到 再将△绕点 逆时针旋转一定角度后,点恰好与点C重合,则平移的距离为( )
A.2 B.3 C.4 D.5
10.把一副三角板按图甲所示的方式放置,其中,把三角板DCE绕点C顺时针旋转得到△(如图乙),AB与 交于点0,连接 则线段 的长为( )
二、填空题(每小题3分,共24分)
11.在如图所示的四组图中,左边图与右边图成中心对称的有_________.
12.把点 先向右平移2个单位,再向上平移4个单位后,得到点N,若点N关于原点的对称点M的坐标为则___________.
13.如图,在△ABC中,∠CAB=45°,将△ABC在平面内绕点A旋转到△的位置,若∠=25°,则旋转角的度数为 __________.
14.如图是用围棋棋子在6×6的正方形网格中摆出的图案,棋子的位置用有序实数对表示,如A点为(5,1),若再摆一黑一白两枚棋子,使这9枚棋子组成的图案既是轴对称图形又是中心对称图形,则下列摆放正确的是__________.(填序号)
①黑(1,5),白(5,5);②黑(3,2),白(3,3);③黑(3,3),白(3,1);④黑(3,1),白(3,3).
15.如图,在 中, 8,将△绕点A逆时针旋转得到 △点B、C的对应点分别为点 与BC相交于点D,当 ∥时,CD的长度为____________.
16.如图,三个边长均为2的正方形重叠在一起,O ,O 是其中两个正方形的对角线的交点,若把这样的n个小正方形按图中的方式摆放,则重叠部分的面积为 ___________ .
17.如图,在△AOB中,OA=AB,顶点A的坐标为(3,4),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得到△,点A的对应点在x轴上,则点的横坐标为__________.
18.如图,在平面直角坐标系中,动点P从原点O出发,水平向左平移1个单位长度,再竖直向下平移1个单位长度得到点P (-1,-1);接着水平向右平移2个单位长度,再竖直向上平移2个单位长度得到点P ;接着水平向左平移3个单位长度,再竖直向下平移3个单位长度得到点P ;接着水平向右平移4个单位长度,再竖直向上平移4个单位长度得到点 ……按此作法进行下去,则点 的坐标为 __________ .
三、解答题(共46分)
19.(10分)如图,四边形ABCD中, ∥且,将△ABC平移到△DEF的位置.
(1)指出平移的方向和平移的距离;
(2)试说明:AD+BC=BF.
20.(10分)如图,在 中, 点D、E分别在AB、AC上, 连接CD,将线段CD绕点C按顺时针方向旋转 后得到线段CF,连接EF.
(1)补全图形;
(2)若 ∥求证:
21.(12分)如图,在平面直角坐标系中,△的三个顶点的坐标分别为
(1)求△的面积;
(2)若△经过平移后得到△A B C ,已知点 的坐标为(4,0),求点 的坐标;
(3)将△绕着点O按顺时针方向旋转 得到△,请画出△并求点
的坐标.
22.(14分)已知△与△是两个大小不同的等腰直角三角形.
(1)如图①所示,连接AE、DB,试判断线段AE和DB之间的数量关系和位置关系,并说明
理由;
(2)如图②所示,连接DB,将线段DB绕点D顺时针旋转 后得到线段DF,连接AF,试
判断线段DE和AF之间的数量关系和位置关系,并说明理由.
参考答案
1.B A项,不是中心对称图形;B项,是中心对称图形;C项,不是中心对称图形;D项,不是中心对称图形.故选B.
2.B A选项,是原图形的轴对称图形,故A不正确;B选项, 绕点B按顺时针方向旋转90°后能得到 故B正确;C选项不正确;D选项, 绕点B按逆时针方向旋转 后能得到 故D不正确.故选B.
3.D A中,经过旋转能由基本图形得到题图②,故该选项不符合题意;B中,经过中心对称和轴对称能由基本图形得到题图②,故该选项不符合题意;C中,经过平移和轴对称能由基本图形得到题图②,故该选项不符合题意;D中,只经过中心对称不能由基本图形得到题图②,故该选项符合题意,故选D.
4.D ∵将△沿射线BC的方向平移2.5 cm后得到△∥∥∥DE,又 故①②③④中的结论均正确.故选D.
和 关于点O成中心对称,
∴ 故A,B,C项结论正确,∵OA与 的大小关系无法确定,∴D项结论不一定正确.故选D.
6.A 由图可知点 的坐标为(0,2).
7.D 如图,作 轴于点E, 轴于点D,则
由题意知 ∴点的坐标为(4,1).故选D.
8.C 如图,点P即为旋转中心,点P的坐标为(4,4).
9.B ∵将△沿射线BC的方向平移,得到△ ,∵将△A′B′C′绕点A′逆时针旋转一定角度后,点 恰好与点C重合, 是等边三角形, ∴平移的距离为3.
10.B ∵∠ACB=∠DEC=90°,∠D=30°,∴ ∴∠ACD=90°-60°=30°,∵旋转的角度为 又∵∠CAB=45°,∴△ACO是等腰直角三角形,
∵DC=14,∴D C=DC=14,在Rt△AOD 中, 故选B.
11.答案 ①②③
解析 根据中心对称的概念,可知①②③中左边图与右边图成中心对称.
12.答案 5
解析 把P(m+3,n-5)先向右平移2个单位,再向上平移4个单位后得到点N,所以N(m+3+2,n-5+4),即N(m+5,n-1),又因为N和M关于原点对称,所以m+5=3,n-1=6,解得m=-2,n=7,所以m+n=5.
13.答案 20°
解析 ∵∠CAB=45°,∠CAB'=25°,
∴旋转角的度数为
14.答案 ④
解析 如图所示,再摆一黑一白两枚棋子:黑(3,1),白(3,3),即可使这9枚棋子组成的图案既是轴对称图形又是中心对称图形,故答案为④.
15.答案
解析 设∥∴∠BAD=∠,由旋转的性质得
∴∠BAD=∠B,∴AD=BD=BC-CD=8-x.在Rt△ACD中,由勾股定理得 即
16.答案 n-1
解析 连接O B,O C,如图:
∵四边形ABCD是正方形,
在 和 中
所在正方形中阴影部分的面积是 同理,另外两个正方形重叠部分的面积也是1,故把n个小正方形按图中的方式摆放,重叠部分的面积为n-1.
17.答案
解析 如图,过点A作 于G,作 于H,
∵点A的坐标为(3,4), 由勾股定理得
设 则 由勾股定理得 解得
∴ ∴点的横坐标为
18.答案 (-1011,-1011)
解析 观察题图可知,奇数点在第三象限,由题意分析可知
19.解析 (1)平移的方向是直线AD的方向,平移的距离是线段AD的长度.
(2)证明:∵将△ABC平移到△DEF的位置,∴CF=AD,
∵CF+BC=BF,∴AD+BC=BF.
20.解析 (1)补全图形,如图所示.
(2)证明:由旋转的性质得∠DCF=90°,DC=FC,∴∠DCE+∠ECF=90°,
∵∠ACB=90°,BC
∥
在△和 中 ∴△BDC≌△EFC(SAS),∴∠BDC=∠EFC=90°.
21.解析 (1)△ABC的面积
经过平移后得到△点C 的坐标为(4,0),∴平移的方式为向下平移3个单位,向右平移5个单位,∴点 的坐标为(2,2).
(3)如图所示, 即为所求,点 的坐标为(3,1).
22.解析 (1) 理由如下:
与△是等腰直角三角形,
如图1,延长DB交AE于点M,
∴在△中, 即AE⊥DB.
(2)DE=AF,DE⊥AF.理由如下:
由题意易知BC=AC,CD=CE,∴BE=AD.
如图2,设ED与AF交于点N,
∵∠EBD=∠C+∠BDC=90°+∠BDC,
∴∠EBD=∠ADF.
在△EBD和△中 ∴△EBD≌△ADF(SAS),∴DE=AF,∠E=∠FAD.
∴∠FAD=∠EDC=45°,∴在△中,
即
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第四章综合测试题
(满分:100分 时间:60分钟)
一、选择题(每小题3分,共30分)
1.下列APP图标中,是中心对称图形的是( )
2.如图,在方格纸中,将Rt△AOB绕点B按顺时针方向旋转 后得到,则下列四个选项中正确的是( )
3.经过下列变换,不能由图①所示的基本图形得到图②的是( )
A.旋转 B.中心对称和轴对称 C.平移和轴对称 D.中心对称
4.如图,在三角形ABC中, 将三角形ABC沿射线BC的方向平移2.5cm后得到三角形DEF,连接AE,AD,有以下结论:①AC∥DF;②AD∥CF; ④DE⊥AC.其中结论正确的有( )
A.1个 B.2个 C.3个 D.4个
5.如图所示,已知△和△关于点O成中心对称,则下列结论不一定正确的是( )
6.△ABC的顶点分别位于格点(网格线的交点)上,建立如图所示的平面直角坐标系,将△ABC先向右平移3个单位长度,再向下平移2个单位长度,得到△,则点A的对应点的坐标是( )
7.如图,将△绕点 旋转 得到 若点A的坐标为 则点 的坐标为( )
8.如图,在平面直角坐标系中,△绕某点顺时针旋转得到△点A、B、C的对应点分别为 则旋转中心的坐标为( )
A.(3,4) B.(3,5) C.(4,4) D.(4,5)
9.如图,在△中, 先将△ABC沿射线BC的方向平移,得到 再将△绕点 逆时针旋转一定角度后,点恰好与点C重合,则平移的距离为( )
A.2 B.3 C.4 D.5
10.把一副三角板按图甲所示的方式放置,其中,把三角板DCE绕点C顺时针旋转得到△(如图乙),AB与 交于点0,连接 则线段 的长为( )
二、填空题(每小题3分,共24分)
11.在如图所示的四组图中,左边图与右边图成中心对称的有_________.
12.把点 先向右平移2个单位,再向上平移4个单位后,得到点N,若点N关于原点的对称点M的坐标为则___________.
13.如图,在△ABC中,∠CAB=45°,将△ABC在平面内绕点A旋转到△的位置,若∠=25°,则旋转角的度数为 __________.
14.如图是用围棋棋子在6×6的正方形网格中摆出的图案,棋子的位置用有序实数对表示,如A点为(5,1),若再摆一黑一白两枚棋子,使这9枚棋子组成的图案既是轴对称图形又是中心对称图形,则下列摆放正确的是__________.(填序号)
①黑(1,5),白(5,5);②黑(3,2),白(3,3);③黑(3,3),白(3,1);④黑(3,1),白(3,3).
15.如图,在 中, 8,将△绕点A逆时针旋转得到 △点B、C的对应点分别为点 与BC相交于点D,当 ∥时,CD的长度为____________.
16.如图,三个边长均为2的正方形重叠在一起,O ,O 是其中两个正方形的对角线的交点,若把这样的n个小正方形按图中的方式摆放,则重叠部分的面积为 ___________ .
17.如图,在△AOB中,OA=AB,顶点A的坐标为(3,4),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得到△,点A的对应点在x轴上,则点的横坐标为__________.
18.如图,在平面直角坐标系中,动点P从原点O出发,水平向左平移1个单位长度,再竖直向下平移1个单位长度得到点P (-1,-1);接着水平向右平移2个单位长度,再竖直向上平移2个单位长度得到点P ;接着水平向左平移3个单位长度,再竖直向下平移3个单位长度得到点P ;接着水平向右平移4个单位长度,再竖直向上平移4个单位长度得到点 ……按此作法进行下去,则点 的坐标为 __________ .
三、解答题(共46分)
19.(10分)如图,四边形ABCD中, ∥且,将△ABC平移到△DEF的位置.
(1)指出平移的方向和平移的距离;
(2)试说明:AD+BC=BF.
20.(10分)如图,在 中, 点D、E分别在AB、AC上, 连接CD,将线段CD绕点C按顺时针方向旋转 后得到线段CF,连接EF.
(1)补全图形;
(2)若 ∥求证:
21.(12分)如图,在平面直角坐标系中,△的三个顶点的坐标分别为
(1)求△的面积;
(2)若△经过平移后得到△A B C ,已知点 的坐标为(4,0),求点 的坐标;
(3)将△绕着点O按顺时针方向旋转 得到△,请画出△并求点
的坐标.
22.(14分)已知△与△是两个大小不同的等腰直角三角形.
(1)如图①所示,连接AE、DB,试判断线段AE和DB之间的数量关系和位置关系,并说明
理由;
(2)如图②所示,连接DB,将线段DB绕点D顺时针旋转 后得到线段DF,连接AF,试
判断线段DE和AF之间的数量关系和位置关系,并说明理由.
参考答案
1.B A项,不是中心对称图形;B项,是中心对称图形;C项,不是中心对称图形;D项,不是中心对称图形.故选B.
2.B A选项,是原图形的轴对称图形,故A不正确;B选项, 绕点B按顺时针方向旋转90°后能得到 故B正确;C选项不正确;D选项, 绕点B按逆时针方向旋转 后能得到 故D不正确.故选B.
3.D A中,经过旋转能由基本图形得到题图②,故该选项不符合题意;B中,经过中心对称和轴对称能由基本图形得到题图②,故该选项不符合题意;C中,经过平移和轴对称能由基本图形得到题图②,故该选项不符合题意;D中,只经过中心对称不能由基本图形得到题图②,故该选项符合题意,故选D.
4.D ∵将△沿射线BC的方向平移2.5 cm后得到△∥∥∥DE,又 故①②③④中的结论均正确.故选D.
和 关于点O成中心对称,
∴ 故A,B,C项结论正确,∵OA与 的大小关系无法确定,∴D项结论不一定正确.故选D.
6.A 由图可知点 的坐标为(0,2).
7.D 如图,作 轴于点E, 轴于点D,则
由题意知 ∴点的坐标为(4,1).故选D.
8.C 如图,点P即为旋转中心,点P的坐标为(4,4).
9.B ∵将△沿射线BC的方向平移,得到△ ,∵将△A′B′C′绕点A′逆时针旋转一定角度后,点 恰好与点C重合, 是等边三角形, ∴平移的距离为3.
10.B ∵∠ACB=∠DEC=90°,∠D=30°,∴ ∴∠ACD=90°-60°=30°,∵旋转的角度为 又∵∠CAB=45°,∴△ACO是等腰直角三角形,
∵DC=14,∴D C=DC=14,在Rt△AOD 中, 故选B.
11.答案 ①②③
解析 根据中心对称的概念,可知①②③中左边图与右边图成中心对称.
12.答案 5
解析 把P(m+3,n-5)先向右平移2个单位,再向上平移4个单位后得到点N,所以N(m+3+2,n-5+4),即N(m+5,n-1),又因为N和M关于原点对称,所以m+5=3,n-1=6,解得m=-2,n=7,所以m+n=5.
13.答案 20°
解析 ∵∠CAB=45°,∠CAB'=25°,
∴旋转角的度数为
14.答案 ④
解析 如图所示,再摆一黑一白两枚棋子:黑(3,1),白(3,3),即可使这9枚棋子组成的图案既是轴对称图形又是中心对称图形,故答案为④.
15.答案
解析 设∥∴∠BAD=∠,由旋转的性质得
∴∠BAD=∠B,∴AD=BD=BC-CD=8-x.在Rt△ACD中,由勾股定理得 即
16.答案 n-1
解析 连接O B,O C,如图:
∵四边形ABCD是正方形,
在 和 中
所在正方形中阴影部分的面积是 同理,另外两个正方形重叠部分的面积也是1,故把n个小正方形按图中的方式摆放,重叠部分的面积为n-1.
17.答案
解析 如图,过点A作 于G,作 于H,
∵点A的坐标为(3,4), 由勾股定理得
设 则 由勾股定理得 解得
∴ ∴点的横坐标为
18.答案 (-1011,-1011)
解析 观察题图可知,奇数点在第三象限,由题意分析可知
19.解析 (1)平移的方向是直线AD的方向,平移的距离是线段AD的长度.
(2)证明:∵将△ABC平移到△DEF的位置,∴CF=AD,
∵CF+BC=BF,∴AD+BC=BF.
20.解析 (1)补全图形,如图所示.
(2)证明:由旋转的性质得∠DCF=90°,DC=FC,∴∠DCE+∠ECF=90°,
∵∠ACB=90°,BC
∥
在△和 中 ∴△BDC≌△EFC(SAS),∴∠BDC=∠EFC=90°.
21.解析 (1)△ABC的面积
经过平移后得到△点C 的坐标为(4,0),∴平移的方式为向下平移3个单位,向右平移5个单位,∴点 的坐标为(2,2).
(3)如图所示, 即为所求,点 的坐标为(3,1).
22.解析 (1) 理由如下:
与△是等腰直角三角形,
如图1,延长DB交AE于点M,
∴在△中, 即AE⊥DB.
(2)DE=AF,DE⊥AF.理由如下:
由题意易知BC=AC,CD=CE,∴BE=AD.
如图2,设ED与AF交于点N,
∵∠EBD=∠C+∠BDC=90°+∠BDC,
∴∠EBD=∠ADF.
在△EBD和△中 ∴△EBD≌△ADF(SAS),∴DE=AF,∠E=∠FAD.
∴∠FAD=∠EDC=45°,∴在△中,
即
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
