27.2.1三角形相似判定(1) 课件
文档属性
| 名称 | 27.2.1三角形相似判定(1) 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 229.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-08-29 16:02:11 | ||
图片预览


文档简介
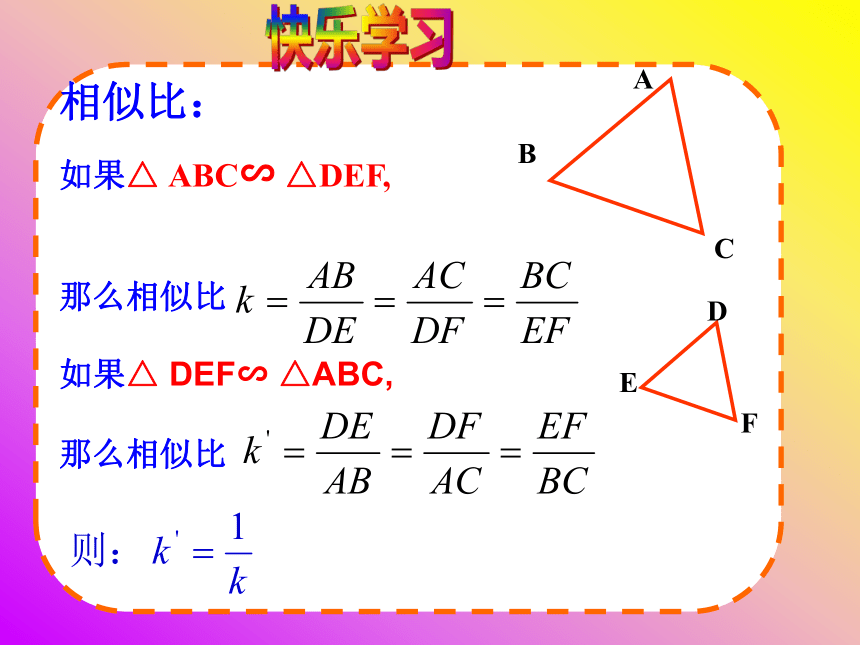
课件22张PPT。1. 对应角_______, 对应边——————的两个
三角形, 叫做相似三角形 相等成比例2. 相似三角形的———————, 各对应边——————。对应角相等成比例如果△ ABC∽ △DEF, 那么∠A=∠D, ∠B=∠E, ∠C=∠F回顾快乐学习相似比:
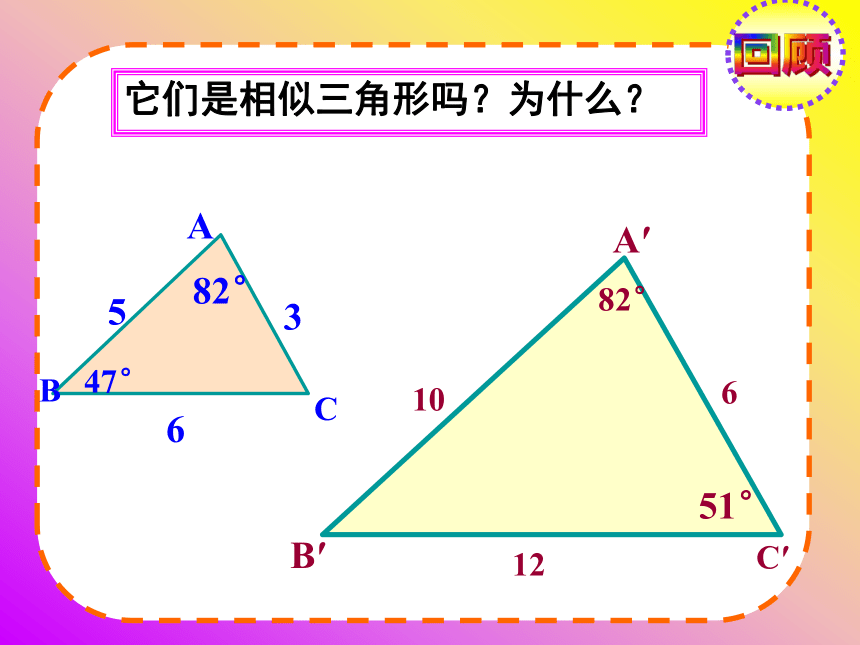
如果△ ABC∽ △DEF,
那么相似比
如果△ DEF∽ △ABC,
那么相似比
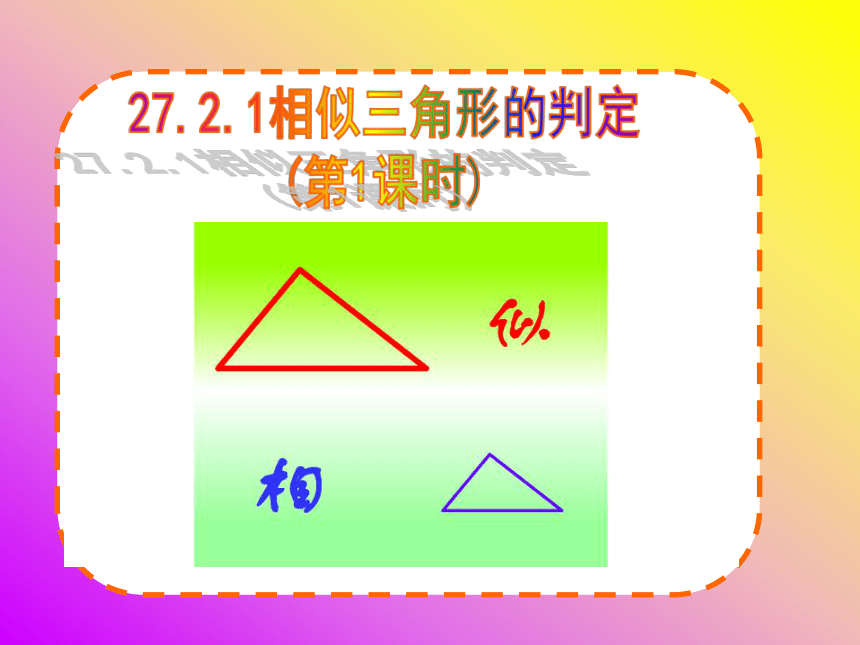
快乐学习它们是相似三角形吗?为什么?回顾27.2.1相似三角形的判定
(第1课时)学习目标1.理解掌握平行线分线段成比例定理.
2.会运用“两个三角形相似的定义判定”和“三角形相似的预备定理”解决简单的问题.
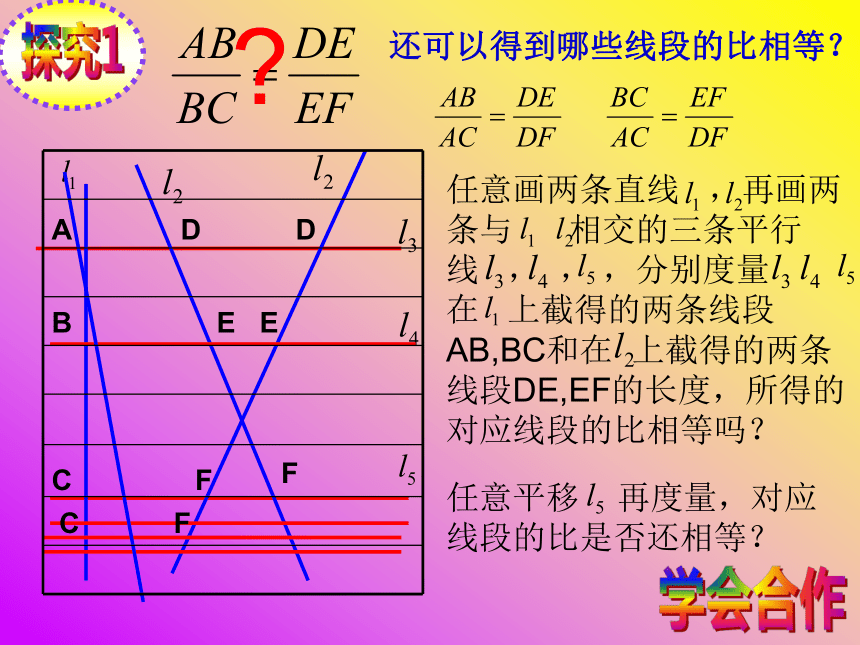
探究1BACDEF?DEF任意画两条直线 ,再画两条与 相交的三条平行线 , , ,分别度量 在 上截得的两条线段AB,BC和在 上截得的两条线段DE,EF的长度,所得的对应线段的比相等吗?任意平移 再度量,对应线段的比是否还相等?
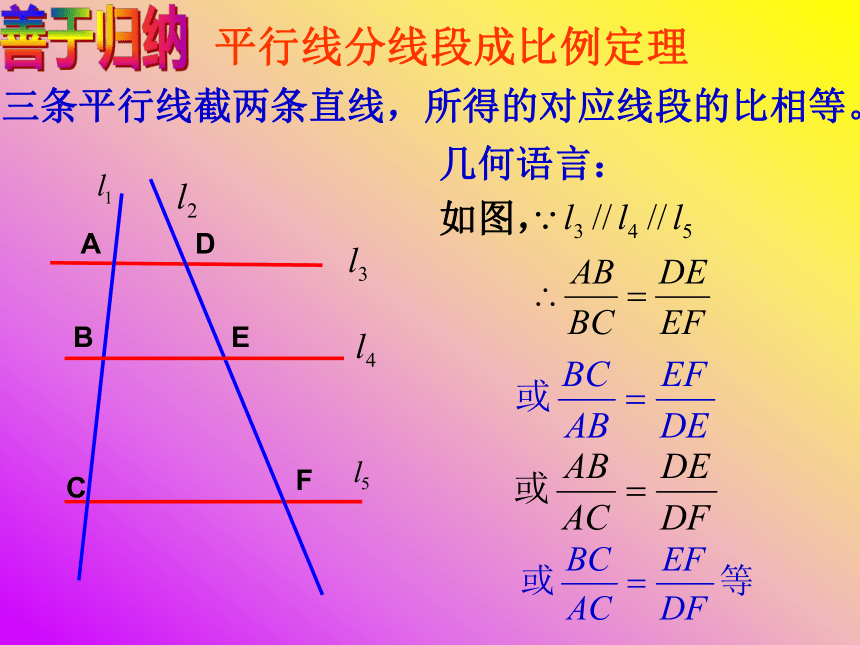
CF还可以得到哪些线段的比相等?学会合作平行线分线段成比例定理三条平行线截两条直线,所得的对应线段的比相等。善于归纳BACDEF几何语言:
如图,
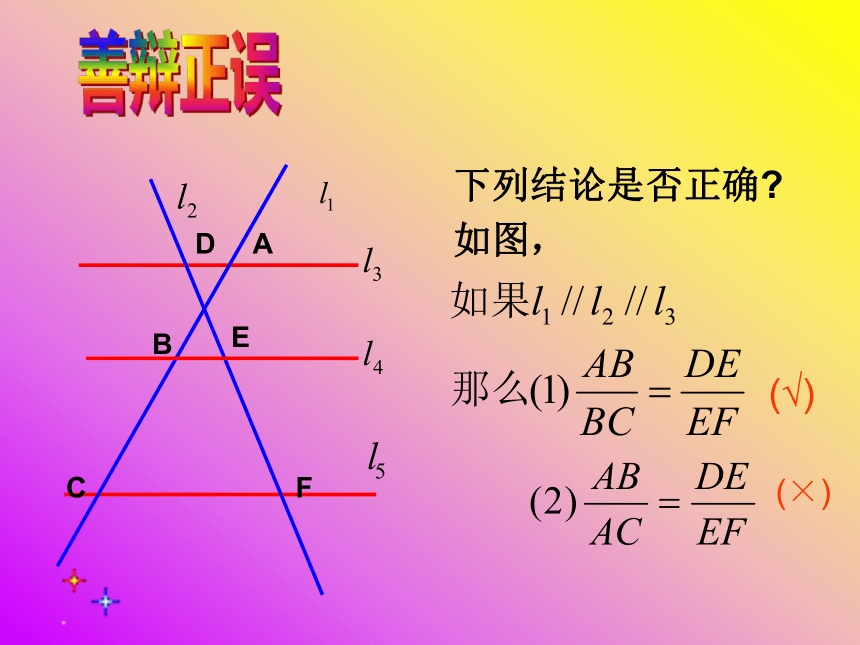
善辩正误BACDEF下列结论是否正确?
如图,
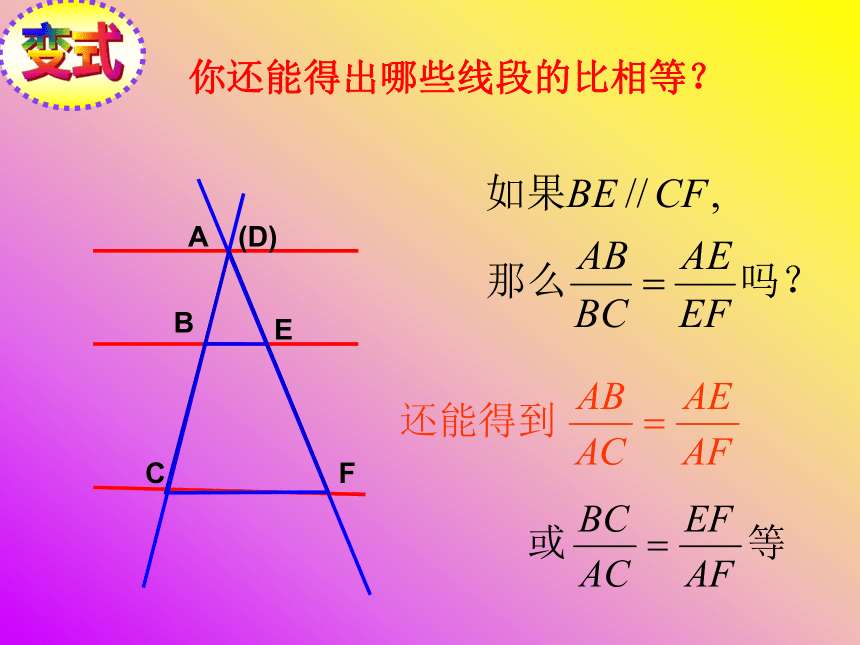
(√)(×)变式BAC(D)EF你还能得出哪些线段的比相等?变式BAC(D)EF变式ADBEC变式ADBEC“A”型 “X”型 (图2)ABCABCDE(图1)善于归纳 平行于三角形一边的直线截其他两边(两边的延长线),所得的对应线段的比相等。 如图,如果DE//BC,ABCDE如果过E作EF//AB交BC于FF 如图,DE//BC,且D是边AB的一点,DE交AC于E, △ADE与△ABC有什么关系?解决问题相似 如图,DE//BC, △ADE与△ABC有什么关系?
说明理由.相似ABCDE证明:在△ADE与△ABC中∠A= ∠A∵ DE//BC∴∠ADE=∠B, ∠AED=∠C过E作EF//AB交BC于F,∵DBFE是平行四边形F∴DE=BF∴△ADE∽△ABC解决问题“A”型 “X”型 理解预备定理:平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似数学语言:
如图 ∵DE∥BC∴△ADE∽△ABC 已知:如图,AB∥EF ∥CD,3图中共有____对相似三角形。 △EOF∽△COD AB∥EF △AOB∽ △FOE AB∥CDEF∥CD△AOB ∽△DOC理解 如图,已知DE ∥ BC,AE=50cm,EC=30cm,BC=70cm,
∠BAC=450,∠ACB=400.
(1)求∠AED和∠ADE的大小;(2)求DE的长.
(2)解: (1)DE ∥ BC△ADE∽△ABC∠AED=∠C=400.△ADE∽△ABC在△ADE中, ∠ADE=1800-400-450=950.学以致用练习:1.如图,在△ABC中,DG∥EH∥FI∥BC,
(1)请找出图中所有的相似三角形;
(2)如果AD=1,DB=3,那么DG:BC=_____。△ADG∽△AEH∽△AFI∽△ABC1:4享受成功
3.如右下图,已知DE∥BC,EF∥AB
AD:DB=2:3 , BC=20cm
则CF= .3:512更上一层楼? 相似三角形的定义? 平行线分线段成比例定理? 相似三角形判定的预备定理分享收获 平行于三角形一边的直线与其它两边(或延长线)相交,所得的三角形与原三角形相似. 三条平行线截两条直线,所得的对应
线段的比相等。? 作业:复习预习教材P40~P43
完成P54第4、5题。
三角形, 叫做相似三角形 相等成比例2. 相似三角形的———————, 各对应边——————。对应角相等成比例如果△ ABC∽ △DEF, 那么∠A=∠D, ∠B=∠E, ∠C=∠F回顾快乐学习相似比:
如果△ ABC∽ △DEF,
那么相似比
如果△ DEF∽ △ABC,
那么相似比
快乐学习它们是相似三角形吗?为什么?回顾27.2.1相似三角形的判定
(第1课时)学习目标1.理解掌握平行线分线段成比例定理.
2.会运用“两个三角形相似的定义判定”和“三角形相似的预备定理”解决简单的问题.
探究1BACDEF?DEF任意画两条直线 ,再画两条与 相交的三条平行线 , , ,分别度量 在 上截得的两条线段AB,BC和在 上截得的两条线段DE,EF的长度,所得的对应线段的比相等吗?任意平移 再度量,对应线段的比是否还相等?
CF还可以得到哪些线段的比相等?学会合作平行线分线段成比例定理三条平行线截两条直线,所得的对应线段的比相等。善于归纳BACDEF几何语言:
如图,
善辩正误BACDEF下列结论是否正确?
如图,
(√)(×)变式BAC(D)EF你还能得出哪些线段的比相等?变式BAC(D)EF变式ADBEC变式ADBEC“A”型 “X”型 (图2)ABCABCDE(图1)善于归纳 平行于三角形一边的直线截其他两边(两边的延长线),所得的对应线段的比相等。 如图,如果DE//BC,ABCDE如果过E作EF//AB交BC于FF 如图,DE//BC,且D是边AB的一点,DE交AC于E, △ADE与△ABC有什么关系?解决问题相似 如图,DE//BC, △ADE与△ABC有什么关系?
说明理由.相似ABCDE证明:在△ADE与△ABC中∠A= ∠A∵ DE//BC∴∠ADE=∠B, ∠AED=∠C过E作EF//AB交BC于F,∵DBFE是平行四边形F∴DE=BF∴△ADE∽△ABC解决问题“A”型 “X”型 理解预备定理:平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似数学语言:
如图 ∵DE∥BC∴△ADE∽△ABC 已知:如图,AB∥EF ∥CD,3图中共有____对相似三角形。 △EOF∽△COD AB∥EF △AOB∽ △FOE AB∥CDEF∥CD△AOB ∽△DOC理解 如图,已知DE ∥ BC,AE=50cm,EC=30cm,BC=70cm,
∠BAC=450,∠ACB=400.
(1)求∠AED和∠ADE的大小;(2)求DE的长.
(2)解: (1)DE ∥ BC△ADE∽△ABC∠AED=∠C=400.△ADE∽△ABC在△ADE中, ∠ADE=1800-400-450=950.学以致用练习:1.如图,在△ABC中,DG∥EH∥FI∥BC,
(1)请找出图中所有的相似三角形;
(2)如果AD=1,DB=3,那么DG:BC=_____。△ADG∽△AEH∽△AFI∽△ABC1:4享受成功
3.如右下图,已知DE∥BC,EF∥AB
AD:DB=2:3 , BC=20cm
则CF= .3:512更上一层楼? 相似三角形的定义? 平行线分线段成比例定理? 相似三角形判定的预备定理分享收获 平行于三角形一边的直线与其它两边(或延长线)相交,所得的三角形与原三角形相似. 三条平行线截两条直线,所得的对应
线段的比相等。? 作业:复习预习教材P40~P43
完成P54第4、5题。
