15.2.2分式的加减(第1课时) 课件(共23张PPT)
文档属性
| 名称 | 15.2.2分式的加减(第1课时) 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 697.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-29 22:32:15 | ||
图片预览








文档简介
(共23张PPT)
人教版八年级数学上册
15.2.2 分式的加减
(第1课时)
你还记得同分母分数加减法法则吗?异分母分数加减法法则又是怎样的呢?想一想分式的加减法又应如何去运算呢?
导入新知
1. 掌握同分母的分式加减法的法则,能熟练地进行同分母的分式加减法的运算.
2.会把异分母的分式通分,转化成同分母的分式相加减.
3.在学习过程中体会类比思想的运用,学会知识的迁移.
素养目标
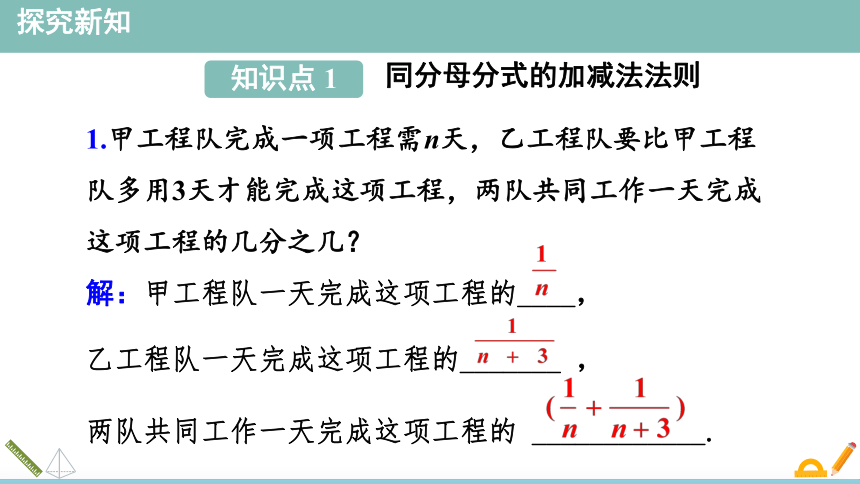
1.甲工程队完成一项工程需n天,乙工程队要比甲工程队多用3天才能完成这项工程,两队共同工作一天完成这项工程的几分之几?
解:甲工程队一天完成这项工程的____,
乙工程队一天完成这项工程的_______ ,
两队共同工作一天完成这项工程的 ____________.
知识点 1
同分母分式的加减法法则
探究新知
2. 2009年,2010年,2011年某地的森林面积(单位:公顷)分别是S1,S2,S3,2011年与2010年相比,森林面积增长率提高了多少?
解:2011年的森林面积增长率是___________,
2010年的森林面积增长率是__________,
2011年与2010年相比,森林面积增长率提高____________.
探究新知
1.同分母分数加减法的法则如何叙述?
探究新知
2.你认为
请计算:
分母不变,把分子相加减.
【同分母的分数加减法的法则】
同分母的分数相加减,
【同分母的分式加减法的法则】
同分母分式相加减,
分母不变,把分子相加减.
探究新知
同分母的分式加减法的法则
例 计算:
解:原式
素养考点 1
同分母分式的加减的计算
归纳总结:
同分母分式的加减,分母不变,分子相加减,当分子是多项式时,先加括号,然后进行计算,结果要化为最简分式或整式.
–1
直接说出运算结果.
.
.
.
.
巩固练习
(1)
(2)
(3)
(4)
计算:
巩固练习
解:原式
解:原式
(1)
(2)
异分母的分数如何加减?
通分,将异分母的分数化为同分母的分数.
知识点 2
异分母分式的加减法的法则
探究新知
想一想
异分母分式的加减应该如何进行?
【异分母的分数加减法的法则】
先通分,变为同分母的分数,再加减.
【异分母的分式加减法的法则】
先通分,变为同分母的分式,再加减.
符号表示:
探究新知
比如:
想一想
例 (1)
素养考点 2
异分母分式的加减的计算
归纳总结:
异分母分式的加减分为两步:第一步通分,化为同分母分式;第二步运用同分母分式的加减法则计算.
探究新知
解:原式
(2)
a2 –4 能分解:
a2 –4 =(a+2)(a–2),
其中 (a–2)恰好为第二个分式的分母,所以 (a+2)(a–2)即为最简公分母.
分子相减时,“减式”要添括号!
探究新知
解:原式
计算:
=x+y
巩固练习
解:原式
=
解:原式
(1)
(2)
巩固练习
计算:
(1)
(2)
解:原式
解:原式
1.计算 ,结果正确的是( )
A.1 B.x C. D.
2. 化简+ 结果是 .
A
连接中考
A. B. C.–1 D.2
C
C
课堂检测
2. 计算
的结果为( )
1.计算 的结果为( )
A.1 B.3 C. D.
3.计算:
(1)
(2)
解:原式
课堂检测
解:原式
阅读下面题目的计算过程.
①
= ②
= ③
= ④
(1)上述计算过程,从哪一步开始错误 _______;
(2)错误原因_________________;
(3)本题的正确结果为: .
②
漏掉了分母
课堂检测
先化简: 当b= –1时,再从–2解:原式=
在–2①若a=–1,分式 无意义;
②若a=0,分式 无意义;
③若a=1,分式 无意义.
所以a在规定的范围内取整数,原式均无意义(或所求值不存在).
课堂检测
分式的加减法法则
课堂小结
注意事项:
①若分子是多项式,则加上括号,然后再加减;
②计算结果一定要化成最简分式或整式.
谢 谢
人教版八年级数学上册
15.2.2 分式的加减
(第1课时)
你还记得同分母分数加减法法则吗?异分母分数加减法法则又是怎样的呢?想一想分式的加减法又应如何去运算呢?
导入新知
1. 掌握同分母的分式加减法的法则,能熟练地进行同分母的分式加减法的运算.
2.会把异分母的分式通分,转化成同分母的分式相加减.
3.在学习过程中体会类比思想的运用,学会知识的迁移.
素养目标
1.甲工程队完成一项工程需n天,乙工程队要比甲工程队多用3天才能完成这项工程,两队共同工作一天完成这项工程的几分之几?
解:甲工程队一天完成这项工程的____,
乙工程队一天完成这项工程的_______ ,
两队共同工作一天完成这项工程的 ____________.
知识点 1
同分母分式的加减法法则
探究新知
2. 2009年,2010年,2011年某地的森林面积(单位:公顷)分别是S1,S2,S3,2011年与2010年相比,森林面积增长率提高了多少?
解:2011年的森林面积增长率是___________,
2010年的森林面积增长率是__________,
2011年与2010年相比,森林面积增长率提高____________.
探究新知
1.同分母分数加减法的法则如何叙述?
探究新知
2.你认为
请计算:
分母不变,把分子相加减.
【同分母的分数加减法的法则】
同分母的分数相加减,
【同分母的分式加减法的法则】
同分母分式相加减,
分母不变,把分子相加减.
探究新知
同分母的分式加减法的法则
例 计算:
解:原式
素养考点 1
同分母分式的加减的计算
归纳总结:
同分母分式的加减,分母不变,分子相加减,当分子是多项式时,先加括号,然后进行计算,结果要化为最简分式或整式.
–1
直接说出运算结果.
.
.
.
.
巩固练习
(1)
(2)
(3)
(4)
计算:
巩固练习
解:原式
解:原式
(1)
(2)
异分母的分数如何加减?
通分,将异分母的分数化为同分母的分数.
知识点 2
异分母分式的加减法的法则
探究新知
想一想
异分母分式的加减应该如何进行?
【异分母的分数加减法的法则】
先通分,变为同分母的分数,再加减.
【异分母的分式加减法的法则】
先通分,变为同分母的分式,再加减.
符号表示:
探究新知
比如:
想一想
例 (1)
素养考点 2
异分母分式的加减的计算
归纳总结:
异分母分式的加减分为两步:第一步通分,化为同分母分式;第二步运用同分母分式的加减法则计算.
探究新知
解:原式
(2)
a2 –4 能分解:
a2 –4 =(a+2)(a–2),
其中 (a–2)恰好为第二个分式的分母,所以 (a+2)(a–2)即为最简公分母.
分子相减时,“减式”要添括号!
探究新知
解:原式
计算:
=x+y
巩固练习
解:原式
=
解:原式
(1)
(2)
巩固练习
计算:
(1)
(2)
解:原式
解:原式
1.计算 ,结果正确的是( )
A.1 B.x C. D.
2. 化简+ 结果是 .
A
连接中考
A. B. C.–1 D.2
C
C
课堂检测
2. 计算
的结果为( )
1.计算 的结果为( )
A.1 B.3 C. D.
3.计算:
(1)
(2)
解:原式
课堂检测
解:原式
阅读下面题目的计算过程.
①
= ②
= ③
= ④
(1)上述计算过程,从哪一步开始错误 _______;
(2)错误原因_________________;
(3)本题的正确结果为: .
②
漏掉了分母
课堂检测
先化简: 当b= –1时,再从–2
在–2
②若a=0,分式 无意义;
③若a=1,分式 无意义.
所以a在规定的范围内取整数,原式均无意义(或所求值不存在).
课堂检测
分式的加减法法则
课堂小结
注意事项:
①若分子是多项式,则加上括号,然后再加减;
②计算结果一定要化成最简分式或整式.
谢 谢
