第七章 随机变量及其分布-专项练习-人教A版(2019)高三一轮复习(Word版含答案)
文档属性
| 名称 | 第七章 随机变量及其分布-专项练习-人教A版(2019)高三一轮复习(Word版含答案) | 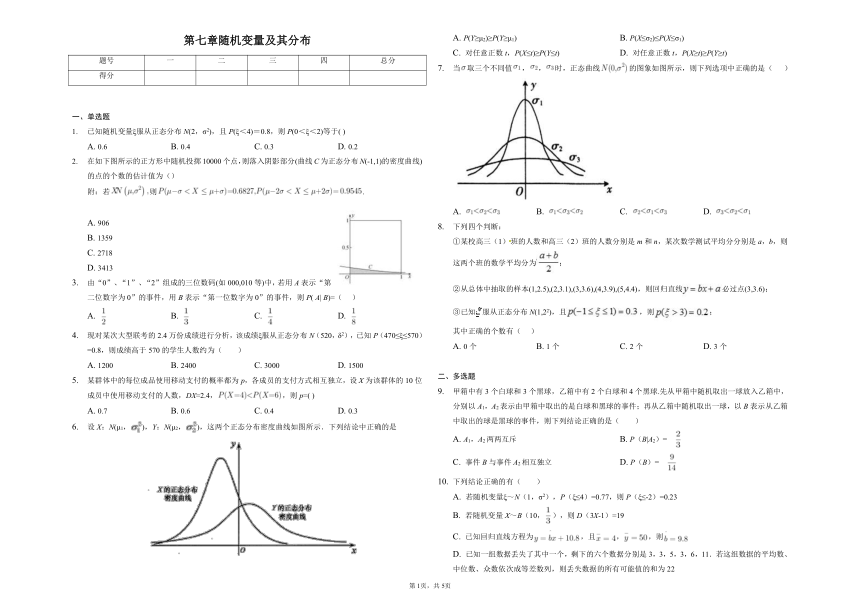 | |
| 格式 | zip | ||
| 文件大小 | 185.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-29 12:34:39 | ||
图片预览


文档简介
第七章随机变量及其分布
题号 一 二 三 四 总分
得分
一、单选题
已知随机变量ξ服从正态分布N(2,σ2),且P(ξ<4)=0.8,则P(0<ξ<2)等于( )
A. 0.6 B. 0.4 C. 0.3 D. 0.2
在如下图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C为正态分布N(-1,1)的密度曲线)的点的个数的估计值为()
附:若则.
A. 906
B. 1359
C. 2718
D. 3413
由“0”、“1”、“2”组成的三位数码(如000,010等)中,若用A表示“第二位数字为0”的事件,用B表示“第一位数字为0”的事件,则P( A| B)=( )
A. B. C. D.
现对某次大型联考的2.4万份成绩进行分析,该成绩ξ服从正态分布N(520,δ2),已知P(470≤ξ≤570)=0.8,则成绩高于570的学生人数约为( )
A. 1200 B. 2400 C. 3000 D. 1500
某群体中的每位成品使用移动支付的概率都为p,各成员的支付方式相互独立,设X为该群体的10位成员中使用移动支付的人数,DX=2.4,,则p=( )
A. 0.7 B. 0.6 C. 0.4 D. 0.3
设X:N(μ1,),Y:N(μ2,),这两个正态分布密度曲线如图所示.下列结论中正确的是
A. P(Y≥μ2)≥P(Y≥μ1) B. P(X≤σ2)≤P(X≤σ1)
C. 对任意正数t,P(X≤t)≥P(Y≤t) D. 对任意正数t,P(X≥t)≥P(Y≥t)
当取三个不同值,,时,正态曲线的图象如图所示,则下列选项中正确的是( )
A. B. C. D.
下列四个判断:
①某校高三(1)班的人数和高三(2)班的人数分别是m和n,某次数学测试平均分分别是a,b,则这两个班的数学平均分为;
②从总体中抽取的样本(1,2.5),(2,3.1),(3,3.6),(4,3.9),(5,4.4),则回归直线必过点(3,3.6);
③已知服从正态分布N(1,22),且,则;
其中正确的个数有( )
A. 0个 B. 1个 C. 2个 D. 3个
二、多选题
甲箱中有3个白球和3个黑球,乙箱中有2个白球和4个黑球.先从甲箱中随机取出一球放入乙箱中,分别以A1,A2表示由甲箱中取出的是白球和黑球的事件;再从乙箱中随机取出一球,以B表示从乙箱中取出的球是黑球的事件,则下列结论正确的是( )
A. A1,A2两两互斥 B. P(B|A2)=
C. 事件B与事件A2相互独立 D. P(B)=
下列结论正确的有( )
A. 若随机变量ξ~N(1,σ2),P(ξ≤4)=0.77,则P(ξ≤-2)=0.23
B. 若随机变量X~B(10,),则D(3X-1)=19
C. 已知回归直线方程为,且,,则
D. 已知一组数据丢失了其中一个,剩下的六个数据分别是3,3,5,3,6,11.若这组数据的平均数、中位数、众数依次成等差数列,则丢失数据的所有可能值的和为22
某市有A,B,C,D四个景点,一位游客来该市游览,已知该游客游览A的概率为,游览B,C,D的概率都是,且该游客是否游览这四个景点相互独立.用随机变量X表示该游客游览的景点个数,则( )
A. 该游客至多游览一个景点的概率为 B.
C. D.
一袋中有大小相同的4个红球和2个白球,则下列结论正确的( )
A. 从中任取3球,恰有一个白球的概率是
B. 从中有放回的取球6次,每次任取一球,则取到红球次数的方差为
C. 现从中不放回的取球2次,每次任取1球,则在第一次取到红球后,第二次再次取到红球的概率为
D. 从中有放回的取球3次,每次任取一球,则至少有一次取到红球的概率为
三、填空题
以下四个命题中:
①某地市高三理科学生有15000名,在一次调研测试中,数学成绩ξ服从正态分布N(100,σ2),已知P(80<ξ≤100)=0.40,若按成绩分层抽样的方式抽取100分试卷进行分析,则应从120分以上(包括120分)的试卷中抽取15分;②用样本相关系数来刻画回归效果时,||越小,说明两个变量相关性越强③在[-4,3]上随机取一个数m,能使函数在R上有零点的概率为;④在某次飞行航程中遭遇恶劣气候,用分层抽样的20名男乘客中有5名晕机,12名女乘客中有8名晕机,在检验这些乘客晕机是否与性别有关时,采用独立性检验,有97%以上的把握认为与性别有关.
P(K2≥k) 0.15 0.1 0.05 0.025
k 2.072 2.706 3.841 5.024
其中真命题的序号为_________.参考公式:
甲乙两袋中各有大小相同的两个红球、一个黄球,分别从两袋中取一个球,恰有一个红球的概率是 .
(1)一个袋中装有6个红球和4个白球(这10个球各不相同),不放回地依次摸出2个球,在第一次摸出红球的条件下,第二次摸出红球的概率为________.
(2)已知随机变量X服从正态分布且则P(X>2)= .
(3)下表是数据x,y的记录表,其中y关于x的线性回归方程是,那么表中t的值是__________.
(4)的展开式中,x2的系数为__________(用数字作答).
已知随机变量X的分布列如表:
X a 2 3 4
P b
若EX=2,则a= (1) ;DX= (2) .
四、解答题
某公司共有10条产品生产线,不超过5条生产线正常工作时,每条生产线每天纯利润为1100元,超过5条生产线正常工作时,超过的生产线每条每天纯利润为800元,原生产线利润保持不变.未开工的生产线每条每天的保养等各种费用共100元.用x表示每天正常工作的生产线条数,用y表示公司每天的纯利润.
(Ⅰ)写出y关于x的函数关系式,并求出纯利润为7700元时工作的生产线条数.
(Ⅱ)为保证新开的生产线正常工作,需对新开的生产线进行检测,现从该生产线上随机抽取100件产品,测量产品数据,用统计方法得到样本的平均数,标准差s=2,绘制如图所示的频率分布直方图.以频率值作为概率估计值.
为检测该生产线生产状况,现从加工的产品中任意抽取一件,记其数据为X,依据以下不等式评判(P表示对应事件的概率)
①
②
③
评判规则为:若至少满足以上两个不等式,则生产状况为优,无需检修;否则需检修生产线.试判断该生产线是否需要检修.
为推动实施健康中国战略,树立国家大卫生、大健康理念.手机APP也推出的多款健康运动软件,如“微信运动”.杨老师的微信朋友圈内有600位好友参与了“微信运动”.他随机选取了40位好友(女20人,男20人),统计他们在某一天的走路步数作为样本.其中,女性好友的走路步数数据记录如下:
5860 8520 7326 6798 7325
8430 3216 7453 11754 9860
8753 6450 7290 4850 10223
9763 7988 9176 6421 5980
男性好友走路的步数情况可分为五个类别:
A(0~2000步)(说明:“0~2000”表示大于等于0,小于等于2000,下同),B(2001~5000步),C(5001~8000步),D(8001~10000步),E(10001步及以上),且B,D,E三种类型人数比例1︰3︰4,将统计结果绘制成如图所示的柱状图.
若某人一天的走路步数超过8000被系统认定为“卫健型”,否则被系统认定为“进步型”.
(1)若以杨老师抽取的好友当天行走步数的频率分布来估计所有微信好友每日走路步数的概率分布,请估计杨老师的微信朋友圈里参与“微信运动”的600名好友中,每天走路步数在5001~10000步的人数;
(2)请根据选取的样本数据完成下面的2×2列联表,并据此判断能否有95%以上的把握认为“认定类型”与“性别”有关
卫健型 讲步型 总计
男 20
女 20
总计 40
(3)若按系统认定类型从选取的样本数据中在男性好友中按比例选取10人,从中任意选取3人,记选到“卫健型”的人数为x;女性好友中按比例选取5人,从中任意选取2人,记选到“卫健型”的人数为y,求事件“|x-y|>1”的概率.
附:,
P(x2>k) 0.10 0.05 0.025 0.010
k 2.706 3.841 5.024 6.635
为增强学生对创办全国文明城市的意识,我校要求全体学生熟记社会主义核心价值观,牢记校规校纪,争做文明学生,现在高二年级学生中进行文明知识测试,已知学生的原始成绩均分布在[50,100]内,发布成绩使用等级制,各等级划分标准见下表,规定:A ,B,C三级为合格等级,D为不合格等级.
百分制 85分及以上 70分到84分 60分到69分 60分以下
等级 A B C D
为了解我校高二年级学生成绩情况,从中抽取了n名学生的原始成绩作为样本进行统计,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示.
(Ⅰ)求n和频率分布直方图中x,y的值;
(Ⅱ)根据样本估计总体的思想,以事件发生的频率作为相应事件发生的概率,若在该校高二学生中任选3人,求至少有1人成绩是合格等级的概率;
(Ⅲ)在选取的样本中从A,C两个等级中随机抽取三名学生调研,记X为抽取的3名学生中等级C的人数,求X的分布列和数学期望.
某小组共10人,利用假期参加义工活动,已知参加义工活动次数为1,2,3的人数分别为3,3,4,现从这10人中随机选出2人作为该组代表参加座谈会.(1)设A为事件“选出的2人参加义工活动次数之和为4”,求事件A发生的概率;
(2)设X为选出的2人参加义工活动次数之差的绝对值,求随机变量X的分布列.
甲、乙两选手比赛,假设每局比赛甲胜的概率是 ,乙胜的概率是,不会出现平局.
(1)如果两人赛3局,求甲恰好胜2局的概率和乙至少胜1局的概率;
(2)如果采用五局三胜制(若甲、乙任何一方先胜3局,则比赛结束,结果为先胜3局者获胜),求甲获胜的概率.
1.【答案】C
2.【答案】B
3.【答案】B
4.【答案】B
5.【答案】B
6.【答案】C
7.【答案】A
8.【答案】B
9.【答案】AD
10.【答案】AC
11.【答案】ABD
12.【答案】ABD
13.【答案】③④
14.【答案】
15.【答案】(1);
(2)0.1;
(3)3;
(4)109
16.【答案】0
17.【答案】解:(Ⅰ)由题意知:当x≤5时,y=1100x-100×(10-x)=1200x-1000,
当5<x≤10时,y=1100×5+800×(x-5)-100×(10-x)=900x+500,
∴
当y=7700时,900x+500=7700,x=8即8条生产线正常工作.
(Ⅱ)μ=14,σ=2,由频率分布直方图得:
∴P(12<X<16)=(0.29+0.11)×2=0.8>0.6826,
P(10<X<18)=0.8+(0.04+0.03)×2=0.94<0.9544,
∴P(8<X<20)=0.94+(0.015+0.005)×2=0.98<0.9974,
∵不满足至少两个不等式,∴该生产线需检修.
18.【答案】解:(1)在样本数据中,男性朋友B类别设为x人,则由题意可知1+x+3+3x+4x=20,可知x=2,故B类别有2人,D类别有6人,E类别有8人,走路步数在5000~10000步的包括C、D两类别共计9人;女性朋友走路步数在5000~10000步共有16人.
用样本数据估计所有微信好友每日走路步数的概率分布,则:
人.
(2)根据题意在抽取的40个样本数据的2×2列联表:
卫健型 进步型 总计
男 14 6 20
女 8 12 20
总计 22 18 40
得,
故没有95%以上的把握认为“评定类型”与“性别”有关.
(3)在男性好友中“卫健型”与“进步型”的比例为7︰3,则选取10人,恰好选取“卫健型”7人,“进步型”3人;在女性好友中“卫健型”与“进步型”的比例为2︰3,选取5人,恰好选取“卫健型”2人,“进步型”3人;
“|x-y|>1”包含“x=3,y=1”,“x=3,y=0”,“x=2,y=0”,“x=0,y=2”,
,,
,,
故.
19.【答案】解:(1)由题意可知,样本容量n==50,x==0.004,
y===0.018;
(2)不合格的概率为0.1,设至少有1人成绩是合格等级为事件A,
∴P(A)=1-0.13=0.999,故至少有1人成绩是合格等级的概率为;
(3)C等级的人数为0.18×50=9人,A等级的为3人,
∴ξ的取值可为0,1,2,3;
∴P(ξ=0)==,P(ξ=1)==,
P(ξ=2)==,P(ξ=3)==,
∴ξ的分布列为
ξ 0 1 2 3
P
Eξ=0×+1×+2×+3×=.
20.【答案】解:(1)从10人中选出2人的选法共有=45种,
事件A:参加次数的和为4,情况有:①1人参加1次,另1人参加3次,②2人都参加2次;
共有+=15种,
∴事件A发生概率:P==.
(Ⅱ)X的可能取值为0,1,2.
P(X=0)==
P(X=1)==,
P(X=2)==,
∴X的分布列为:
X 0 1 2
P
.
21.【答案】解:(1)甲恰好胜2局的概率 ;
乙至少胜1局的概率 ;
(2)打3局甲获胜: ;打4局甲获胜: ;
打5局甲获胜: ,
因此甲获胜的概率为 .
第4页,共5页
第3页,共5页
题号 一 二 三 四 总分
得分
一、单选题
已知随机变量ξ服从正态分布N(2,σ2),且P(ξ<4)=0.8,则P(0<ξ<2)等于( )
A. 0.6 B. 0.4 C. 0.3 D. 0.2
在如下图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C为正态分布N(-1,1)的密度曲线)的点的个数的估计值为()
附:若则.
A. 906
B. 1359
C. 2718
D. 3413
由“0”、“1”、“2”组成的三位数码(如000,010等)中,若用A表示“第二位数字为0”的事件,用B表示“第一位数字为0”的事件,则P( A| B)=( )
A. B. C. D.
现对某次大型联考的2.4万份成绩进行分析,该成绩ξ服从正态分布N(520,δ2),已知P(470≤ξ≤570)=0.8,则成绩高于570的学生人数约为( )
A. 1200 B. 2400 C. 3000 D. 1500
某群体中的每位成品使用移动支付的概率都为p,各成员的支付方式相互独立,设X为该群体的10位成员中使用移动支付的人数,DX=2.4,,则p=( )
A. 0.7 B. 0.6 C. 0.4 D. 0.3
设X:N(μ1,),Y:N(μ2,),这两个正态分布密度曲线如图所示.下列结论中正确的是
A. P(Y≥μ2)≥P(Y≥μ1) B. P(X≤σ2)≤P(X≤σ1)
C. 对任意正数t,P(X≤t)≥P(Y≤t) D. 对任意正数t,P(X≥t)≥P(Y≥t)
当取三个不同值,,时,正态曲线的图象如图所示,则下列选项中正确的是( )
A. B. C. D.
下列四个判断:
①某校高三(1)班的人数和高三(2)班的人数分别是m和n,某次数学测试平均分分别是a,b,则这两个班的数学平均分为;
②从总体中抽取的样本(1,2.5),(2,3.1),(3,3.6),(4,3.9),(5,4.4),则回归直线必过点(3,3.6);
③已知服从正态分布N(1,22),且,则;
其中正确的个数有( )
A. 0个 B. 1个 C. 2个 D. 3个
二、多选题
甲箱中有3个白球和3个黑球,乙箱中有2个白球和4个黑球.先从甲箱中随机取出一球放入乙箱中,分别以A1,A2表示由甲箱中取出的是白球和黑球的事件;再从乙箱中随机取出一球,以B表示从乙箱中取出的球是黑球的事件,则下列结论正确的是( )
A. A1,A2两两互斥 B. P(B|A2)=
C. 事件B与事件A2相互独立 D. P(B)=
下列结论正确的有( )
A. 若随机变量ξ~N(1,σ2),P(ξ≤4)=0.77,则P(ξ≤-2)=0.23
B. 若随机变量X~B(10,),则D(3X-1)=19
C. 已知回归直线方程为,且,,则
D. 已知一组数据丢失了其中一个,剩下的六个数据分别是3,3,5,3,6,11.若这组数据的平均数、中位数、众数依次成等差数列,则丢失数据的所有可能值的和为22
某市有A,B,C,D四个景点,一位游客来该市游览,已知该游客游览A的概率为,游览B,C,D的概率都是,且该游客是否游览这四个景点相互独立.用随机变量X表示该游客游览的景点个数,则( )
A. 该游客至多游览一个景点的概率为 B.
C. D.
一袋中有大小相同的4个红球和2个白球,则下列结论正确的( )
A. 从中任取3球,恰有一个白球的概率是
B. 从中有放回的取球6次,每次任取一球,则取到红球次数的方差为
C. 现从中不放回的取球2次,每次任取1球,则在第一次取到红球后,第二次再次取到红球的概率为
D. 从中有放回的取球3次,每次任取一球,则至少有一次取到红球的概率为
三、填空题
以下四个命题中:
①某地市高三理科学生有15000名,在一次调研测试中,数学成绩ξ服从正态分布N(100,σ2),已知P(80<ξ≤100)=0.40,若按成绩分层抽样的方式抽取100分试卷进行分析,则应从120分以上(包括120分)的试卷中抽取15分;②用样本相关系数来刻画回归效果时,||越小,说明两个变量相关性越强③在[-4,3]上随机取一个数m,能使函数在R上有零点的概率为;④在某次飞行航程中遭遇恶劣气候,用分层抽样的20名男乘客中有5名晕机,12名女乘客中有8名晕机,在检验这些乘客晕机是否与性别有关时,采用独立性检验,有97%以上的把握认为与性别有关.
P(K2≥k) 0.15 0.1 0.05 0.025
k 2.072 2.706 3.841 5.024
其中真命题的序号为_________.参考公式:
甲乙两袋中各有大小相同的两个红球、一个黄球,分别从两袋中取一个球,恰有一个红球的概率是 .
(1)一个袋中装有6个红球和4个白球(这10个球各不相同),不放回地依次摸出2个球,在第一次摸出红球的条件下,第二次摸出红球的概率为________.
(2)已知随机变量X服从正态分布且则P(X>2)= .
(3)下表是数据x,y的记录表,其中y关于x的线性回归方程是,那么表中t的值是__________.
(4)的展开式中,x2的系数为__________(用数字作答).
已知随机变量X的分布列如表:
X a 2 3 4
P b
若EX=2,则a= (1) ;DX= (2) .
四、解答题
某公司共有10条产品生产线,不超过5条生产线正常工作时,每条生产线每天纯利润为1100元,超过5条生产线正常工作时,超过的生产线每条每天纯利润为800元,原生产线利润保持不变.未开工的生产线每条每天的保养等各种费用共100元.用x表示每天正常工作的生产线条数,用y表示公司每天的纯利润.
(Ⅰ)写出y关于x的函数关系式,并求出纯利润为7700元时工作的生产线条数.
(Ⅱ)为保证新开的生产线正常工作,需对新开的生产线进行检测,现从该生产线上随机抽取100件产品,测量产品数据,用统计方法得到样本的平均数,标准差s=2,绘制如图所示的频率分布直方图.以频率值作为概率估计值.
为检测该生产线生产状况,现从加工的产品中任意抽取一件,记其数据为X,依据以下不等式评判(P表示对应事件的概率)
①
②
③
评判规则为:若至少满足以上两个不等式,则生产状况为优,无需检修;否则需检修生产线.试判断该生产线是否需要检修.
为推动实施健康中国战略,树立国家大卫生、大健康理念.手机APP也推出的多款健康运动软件,如“微信运动”.杨老师的微信朋友圈内有600位好友参与了“微信运动”.他随机选取了40位好友(女20人,男20人),统计他们在某一天的走路步数作为样本.其中,女性好友的走路步数数据记录如下:
5860 8520 7326 6798 7325
8430 3216 7453 11754 9860
8753 6450 7290 4850 10223
9763 7988 9176 6421 5980
男性好友走路的步数情况可分为五个类别:
A(0~2000步)(说明:“0~2000”表示大于等于0,小于等于2000,下同),B(2001~5000步),C(5001~8000步),D(8001~10000步),E(10001步及以上),且B,D,E三种类型人数比例1︰3︰4,将统计结果绘制成如图所示的柱状图.
若某人一天的走路步数超过8000被系统认定为“卫健型”,否则被系统认定为“进步型”.
(1)若以杨老师抽取的好友当天行走步数的频率分布来估计所有微信好友每日走路步数的概率分布,请估计杨老师的微信朋友圈里参与“微信运动”的600名好友中,每天走路步数在5001~10000步的人数;
(2)请根据选取的样本数据完成下面的2×2列联表,并据此判断能否有95%以上的把握认为“认定类型”与“性别”有关
卫健型 讲步型 总计
男 20
女 20
总计 40
(3)若按系统认定类型从选取的样本数据中在男性好友中按比例选取10人,从中任意选取3人,记选到“卫健型”的人数为x;女性好友中按比例选取5人,从中任意选取2人,记选到“卫健型”的人数为y,求事件“|x-y|>1”的概率.
附:,
P(x2>k) 0.10 0.05 0.025 0.010
k 2.706 3.841 5.024 6.635
为增强学生对创办全国文明城市的意识,我校要求全体学生熟记社会主义核心价值观,牢记校规校纪,争做文明学生,现在高二年级学生中进行文明知识测试,已知学生的原始成绩均分布在[50,100]内,发布成绩使用等级制,各等级划分标准见下表,规定:A ,B,C三级为合格等级,D为不合格等级.
百分制 85分及以上 70分到84分 60分到69分 60分以下
等级 A B C D
为了解我校高二年级学生成绩情况,从中抽取了n名学生的原始成绩作为样本进行统计,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示.
(Ⅰ)求n和频率分布直方图中x,y的值;
(Ⅱ)根据样本估计总体的思想,以事件发生的频率作为相应事件发生的概率,若在该校高二学生中任选3人,求至少有1人成绩是合格等级的概率;
(Ⅲ)在选取的样本中从A,C两个等级中随机抽取三名学生调研,记X为抽取的3名学生中等级C的人数,求X的分布列和数学期望.
某小组共10人,利用假期参加义工活动,已知参加义工活动次数为1,2,3的人数分别为3,3,4,现从这10人中随机选出2人作为该组代表参加座谈会.(1)设A为事件“选出的2人参加义工活动次数之和为4”,求事件A发生的概率;
(2)设X为选出的2人参加义工活动次数之差的绝对值,求随机变量X的分布列.
甲、乙两选手比赛,假设每局比赛甲胜的概率是 ,乙胜的概率是,不会出现平局.
(1)如果两人赛3局,求甲恰好胜2局的概率和乙至少胜1局的概率;
(2)如果采用五局三胜制(若甲、乙任何一方先胜3局,则比赛结束,结果为先胜3局者获胜),求甲获胜的概率.
1.【答案】C
2.【答案】B
3.【答案】B
4.【答案】B
5.【答案】B
6.【答案】C
7.【答案】A
8.【答案】B
9.【答案】AD
10.【答案】AC
11.【答案】ABD
12.【答案】ABD
13.【答案】③④
14.【答案】
15.【答案】(1);
(2)0.1;
(3)3;
(4)109
16.【答案】0
17.【答案】解:(Ⅰ)由题意知:当x≤5时,y=1100x-100×(10-x)=1200x-1000,
当5<x≤10时,y=1100×5+800×(x-5)-100×(10-x)=900x+500,
∴
当y=7700时,900x+500=7700,x=8即8条生产线正常工作.
(Ⅱ)μ=14,σ=2,由频率分布直方图得:
∴P(12<X<16)=(0.29+0.11)×2=0.8>0.6826,
P(10<X<18)=0.8+(0.04+0.03)×2=0.94<0.9544,
∴P(8<X<20)=0.94+(0.015+0.005)×2=0.98<0.9974,
∵不满足至少两个不等式,∴该生产线需检修.
18.【答案】解:(1)在样本数据中,男性朋友B类别设为x人,则由题意可知1+x+3+3x+4x=20,可知x=2,故B类别有2人,D类别有6人,E类别有8人,走路步数在5000~10000步的包括C、D两类别共计9人;女性朋友走路步数在5000~10000步共有16人.
用样本数据估计所有微信好友每日走路步数的概率分布,则:
人.
(2)根据题意在抽取的40个样本数据的2×2列联表:
卫健型 进步型 总计
男 14 6 20
女 8 12 20
总计 22 18 40
得,
故没有95%以上的把握认为“评定类型”与“性别”有关.
(3)在男性好友中“卫健型”与“进步型”的比例为7︰3,则选取10人,恰好选取“卫健型”7人,“进步型”3人;在女性好友中“卫健型”与“进步型”的比例为2︰3,选取5人,恰好选取“卫健型”2人,“进步型”3人;
“|x-y|>1”包含“x=3,y=1”,“x=3,y=0”,“x=2,y=0”,“x=0,y=2”,
,,
,,
故.
19.【答案】解:(1)由题意可知,样本容量n==50,x==0.004,
y===0.018;
(2)不合格的概率为0.1,设至少有1人成绩是合格等级为事件A,
∴P(A)=1-0.13=0.999,故至少有1人成绩是合格等级的概率为;
(3)C等级的人数为0.18×50=9人,A等级的为3人,
∴ξ的取值可为0,1,2,3;
∴P(ξ=0)==,P(ξ=1)==,
P(ξ=2)==,P(ξ=3)==,
∴ξ的分布列为
ξ 0 1 2 3
P
Eξ=0×+1×+2×+3×=.
20.【答案】解:(1)从10人中选出2人的选法共有=45种,
事件A:参加次数的和为4,情况有:①1人参加1次,另1人参加3次,②2人都参加2次;
共有+=15种,
∴事件A发生概率:P==.
(Ⅱ)X的可能取值为0,1,2.
P(X=0)==
P(X=1)==,
P(X=2)==,
∴X的分布列为:
X 0 1 2
P
.
21.【答案】解:(1)甲恰好胜2局的概率 ;
乙至少胜1局的概率 ;
(2)打3局甲获胜: ;打4局甲获胜: ;
打5局甲获胜: ,
因此甲获胜的概率为 .
第4页,共5页
第3页,共5页
