第2章 图形的轴对称单元测试卷(困难)(含答案)
文档属性
| 名称 | 第2章 图形的轴对称单元测试卷(困难)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 344.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-29 16:52:37 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
青岛版初中数学八年级上册第二单元《图形的轴对称》测试卷
考试范围:第二章;考试时间:120分钟;总分120分
学校:___________姓名:___________班级:___________考号:___________
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上,写在试卷上无效。
3.考试结束后,本试卷和答题卡一并交回。
第I卷(选择题)
一、选择题(本大题共12小题,共36分)
如图所示是一台球桌面的示意图,图中小正方形的边长均相等,黑球放在如图所示的位置,经白球撞击后沿箭头方向运动,经桌边反弹最后进入球洞的序号是( )
A. B. C. D.
在日常生活中,有一些含有特殊数字规律的车牌号码,如川,川,川等,这些牌照中的五个数字都是关于中间的一个数字“对称”的我们不妨把这样的牌照叫做数字对称牌照,如果让你负责制作以为字母“”后的第一个数字,且有五个数字的“数字对称”牌照,那么最多可制作( )
A. 个 B. 个 C. 个 D. 个
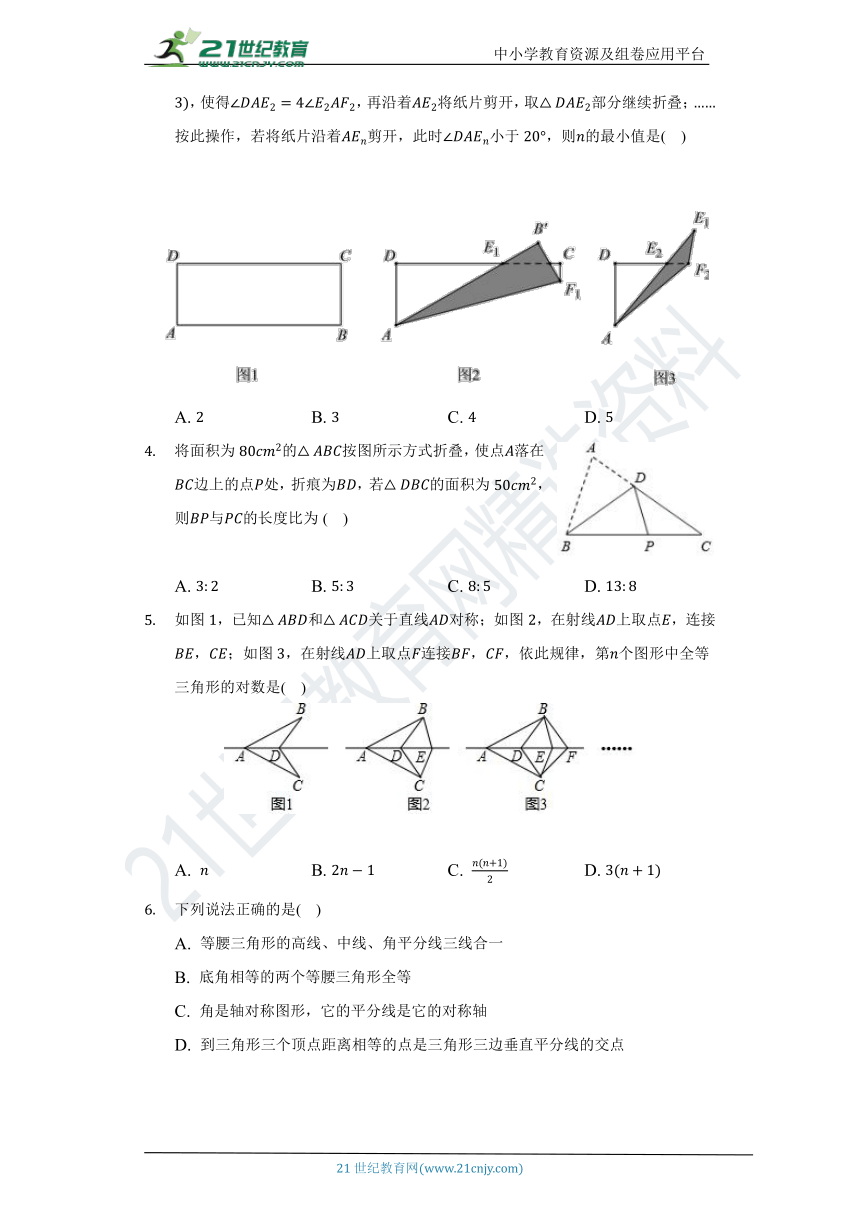
将一张长方形纸片如图进行折叠操作.第一次折叠后如图,使得,再沿着将纸片剪开,取部分继续折叠;第二次折叠后如图,使得,再沿着将纸片剪开,取部分继续折叠;按此操作,若将纸片沿着剪开,此时小于,则的最小值是( )
A. B. C. D.
将面积为的按图所示方式折叠,使点落在边上的点处,折痕为,若的面积为,则与的长度比为( )
A. B. C. D.
如图,已知和关于直线对称;如图,在射线上取点,连接,;如图,在射线上取点连接,,依此规律,第个图形中全等三角形的对数是( )
A. B. C. D.
下列说法正确的是( )
A. 等腰三角形的高线、中线、角平分线三线合一
B. 底角相等的两个等腰三角形全等
C. 角是轴对称图形,它的平分线是它的对称轴
D. 到三角形三个顶点距离相等的点是三角形三边垂直平分线的交点
在联谊会上,有、、三名选手站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在的( )
A. 三边中线的交点 B. 三条角平分线的交点
C. 三边中垂线的交点 D. 三边上高的交点
如图,在中,和的平分线,相交于点,交于,交于,过点作于,下列四个结论:;当时,;若,,则其中正确的是( )
A. B. C. D.
如图,中,、的角平分线、交于点,延长、,,,则下列结论中正确的个数( )
平分; ;;
A. 个 B. 个 C. 个 D. 个
等腰三角形的一个角是,则它的底角是( )
A. B. 或 C. 或 D.
如图,在菱形中,,的两顶点,分别落在边,上,从给出的四个条件中任选一个:;;;能够推出为等边三角形的是( )
A. B. C. D.
如图,,平分,且若点,分别在射线,上,且是边长为整数的等边三角形,则满足上述条件的点有参考数据: ( )
A. 个以上 B. 个 C. 个 D. 个
第II卷(非选择题)
二、填空题(本大题共4小题,共12分)
如图,已知中,,点是的中点,将沿所在的直线翻折,点落在点处,,且交于点,:的值为______.
如图,在中,,,,点为边的中点,点为边上一动点,连接,作关于直线的轴对称图形,点的对应点为点,连接,则长度的取值范围为______.
在四边形中,,,,为上一点,,且,的延长线于连接交对角线于下列结论:≌;垂直平分;;平分其中结论正确的是______填序号
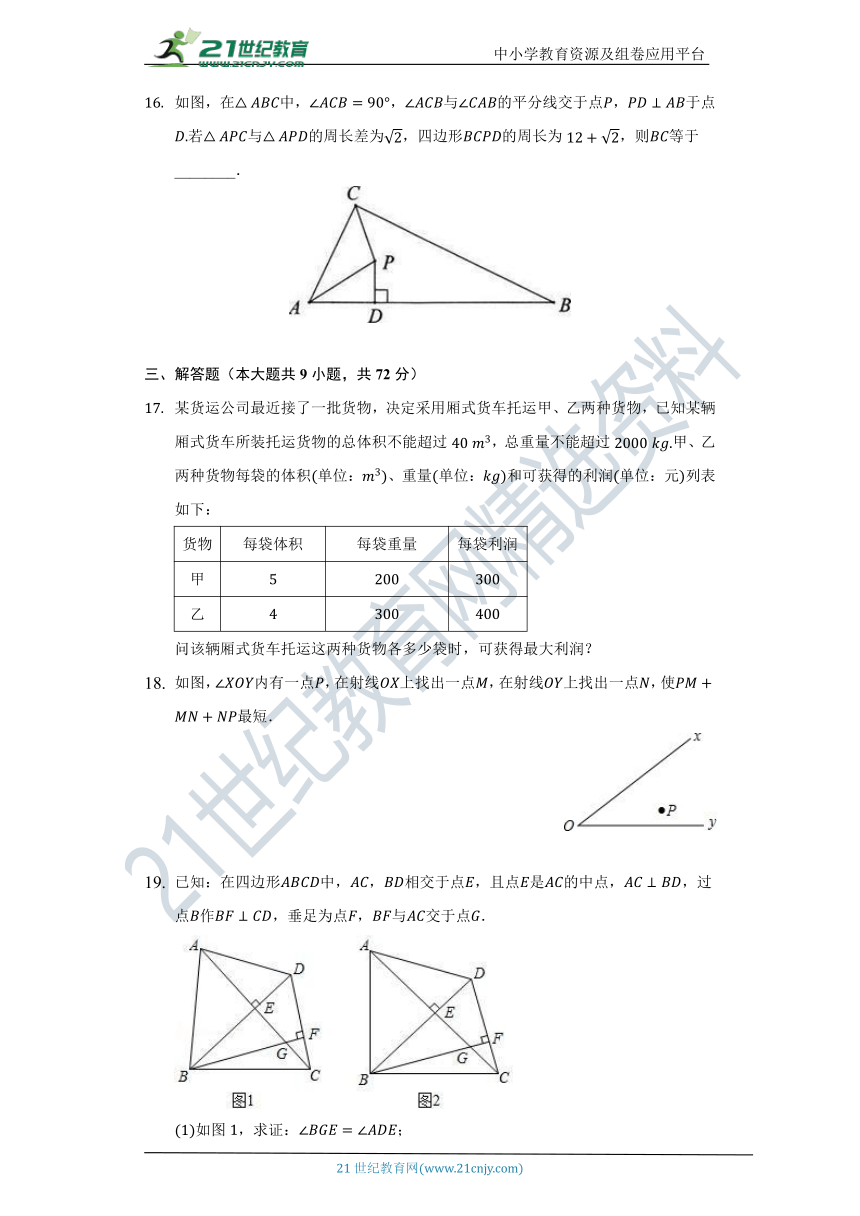
如图,在中,,与的平分线交于点,于点若与的周长差为,四边形的周长为,则等于________.
三、解答题(本大题共9小题,共72分)
某货运公司最近接了一批货物,决定采用厢式货车托运甲、乙两种货物,已知某辆厢式货车所装托运货物的总体积不能超过,总重量不能超过甲、乙两种货物每袋的体积单位:、重量单位:和可获得的利润单位:元列表如下:
货物 每袋体积 每袋重量 每袋利润
甲
乙
问该辆厢式货车托运这两种货物各多少袋时,可获得最大利润?
如图,内有一点,在射线上找出一点,在射线上找出一点,使最短.
已知:在四边形中,,相交于点,且点是的中点,,过点作,垂足为点,与交于点.
如图,求证:;
如图,若;
求证:;
若,的面积为,求四边形的面积.
如图,为的角平分线,于点,于点,连接交于点.
求证:垂直平分;
若,写出与之间的数量关系,不需证明.
如图,中
尺规作图:作的垂直平分线,交于点,交于点 .
在图中连,如果,,求的周长.
如图,在中,,平分,交于点,.
求证:;
若,则的周长为______.
如图,在的两边,上分别取,,和相交于点.
求证:点在的平分线上.
已知:为等边三角形,点为射线上一点,点为射线上一点,.
如图,当在的延长线上且时,是的中线吗?请说明理由;
如图,当在的延长线上时,等于吗?请说明理由;
如图,当在线段的延长线上,在线段上时,请直接写出、、的数量关系.
已知为等边三角形,点、分别在直线、上,且.
如图,若点、分别是、边上的点,连接、交于点,过点作,使,连接,则______填度数;
在的条件下,猜想与存在什么关系,并证明;
如图,若点、分别是、延长线上的点,中结论是否仍然成立?请给出判断并证明.
答案和解析
1.【答案】
【解析】
【分析】
本题主要考查了生活中的轴对称现象;结合轴对称的知识画出图形是解答本题的关键.入射光线与水平线的夹角等于反射光线与水平线的夹角,动手操作即可.
【解答】
解:如图,求最后落入球洞;
故选A.
2.【答案】
【解析】解:以为字母“”后的第一个数字且有五个数字的“数字对称”牌照,
第一位为,则第五个也是
第三位可以是中任意一个,有种可能.
第二、第四位可以是中任意一个,有种可能.
所以开头的组合最多是个.
故选C.
以开头,那么最后一位数字也只能是,那么只有中间位可以随便取,又因为第二位和第四位数字必须一样,实际上只有第二位和第三位可以取十个数字,所以只有个.
本题考查了轴对称图形的知识,注意掌握对称的要求,正确分析各个数位的数字情况.
3.【答案】
【解析】
【分析】
本题考查了图形折叠的规律问题,由题意找出规律,列出不等式解出即可.
【解答】
解:由题意得:第一次折叠后,
第一次折叠后,
第次折叠后,
所以,
则的最小值为,
故选C.
4.【答案】
【解析】
【分析】
本题考查了折叠的性质:折叠前后的两个三角形是全等三角形,它们的面积相等.由题意分别计算出与的面积,从而::,问题可解.
【解答】
解:由题意可得:
由折叠性质可知,,
::::.
故选A.
5.【答案】
【解析】
【分析】
此题主要考查了三角形全等的判定以及规律的归纳,解题的关键是根据条件证出图形中有几对三角形全等,然后寻找规律.
根据条件可得图中有对三角形全等;图中可证出,,有对三角形全等;图中有对三角形全等,根据数据可分析出第个图形中全等三角形的对数.
【解答】
解:和关于直线对称,
.
在与中
,
.
图中有对三角形全等;
同理图中,,
,
,
,
在和中
,
,
图中有对三角形全等;
同理:图中有对三角形全等;
由此发现:第个图形中全等三角形的对数是.
故选:.
6.【答案】
【解析】
【分析】
本题主要考查了等腰三角形的性质,全等三角形的判定,轴对称图形的定义,线段垂直平分线的性质,关键是结合各个知识点对各个选项依次判断.
【解答】
解:等腰三角形底边上的高线、中线,顶角的平分线三线合一,故本项错误;
B.底角相等的两个等腰三角形,即两个等腰三角形的三个角对应相等,这两个三角形不一定全等,故本项错误;
C.角是轴对称图形,它的平分线所在直线是它的对称轴,故本项错误;
D.三角形三个顶点距离相等的点是三角形三边垂直平分线的交点,故本项正确;
故选D.
7.【答案】
【解析】解:三角形的三条垂直平分线的交点到三角形各顶点的距离相等,
凳子应放在的三条垂直平分线的交点最适当.
故选:.
为使游戏公平,要使凳子到三个人的距离相等,于是利用线段垂直平分线上的点到线段两端的距离相等可知,要放在三边中垂线的交点上.
本题主要考查了线段垂直平分线的性质的应用;利用所学的数学知识解决实际问题是一种能力,要注意培养.想到要使凳子到三个人的距离相等是正确解答本题的关键.
8.【答案】
【解析】解:和的平分线相交于点,
,,
,正确;
,
,
,分别是与的平分线,
,
,
,
,
如图,在上取一点,使,
是的角平分线,
,
在和中,,
≌,
,
,
,
在和中,,
≌,
,
,故正确;
作于,于,
和的平分线相交于点,
点在的平分线上,
,
,正确.
故选:.
由角平分线的定义结合三角形的内角和的可求解与的关系,进而判定;在上取一点,使,证得≌,得到,再证得≌,得到,进而判定正确;作于,于,根据三角形的面积可证得正确.
本题主要考查了三角形内角和定理,三角形外角的性质,三角形全等的性质和判定,正确作出辅助线证得≌,得到,是解决问题的关键.
9.【答案】
【解析】
【分析】
本题考查了角平分线的性质与判定,全等三角形的判定与性质,三角形的外角性质,掌握角平分线的性质判定是解题的关键.
作于,由角平分线的性质得出,,得出,即可得出正确;
首先证出,证明≌,得出,同理:≌,得出,即可得出正确;
由角平分线和三角形的外角性质得出,,得出,即可得出正确;
由全等三角形的性质得出,,即可得出正确.
【解答】
解:作于,
平分,平分,,,
,,
,
点在的角平分线上,故正确;
,,
,
,
在和中,
,
≌,
,
同理:≌,
,
,
,正确;
平分,平分,
,,
,正确;
≌,
,
同理:≌,
,
,正确;
故选:.
10.【答案】
【解析】解:当底角为时,则底角为,
当顶角为时,由三角形内角和定理可求得底角为:,
所以底角为或,
故选:.
分这个角为底角和顶角两种情况讨论即可.
本题主要考查等腰三角形的性质,分两种情况讨论是解题的关键.
11.【答案】
【解析】
【分析】
本题考查等边三角形的判定与性质.
根据等边三角形的判定方法分别对四个条件一一推理判断即可.
【解答】
解:能够推出为等边三角形
理由如下:
如图
四边形是菱形,
,
和都是等边三角形,
,
,
在和中,
,
,
为等边三角形.
能够推出为等边三角形
理由如下:
如图
四边形是菱形,
.
.
是等边三角形,
在上截取,则是等边三角形,
,
,又因为,
.
在与中,
.
,
.
,
是等边三角形
不能推出为等边三角形
理由如下:
如图
四边形是菱形,
,
和都是等边三角形,
,,
因为,,,边边角不能判定与全等,
故不能推出为等边三角形;
不能推出为等边三角形
理由如下:
如图
在上截取,
四边形是菱形,
,
、和都是等边三角形,
,
,
因为,,,边边角不能判定与全等,
故不能推出为等边三角形.
12.【答案】
【解析】
【分析】
本题考等边三角形判定和性质、全等三角形的判和性质、角平分线的定义,勾股定理.解的关键是添加辅助线,构造等边三角形,由此即可得出结论.
【解答】
解:在、上截取,作.
平分,
,是等边角形,
,,
,
在和中,
,
,
,
是等边三角形,
当时,,
边长为整数,,分别在射线,上,
的整数,
或,
这样的整数只有和,两边各有两个满足条件的三角形,即满足上述条件的点有个.
故选B.
13.【答案】
【解析】解:连接,交于点,如图,
设,,
是的中点,,
是有斜边上的中线,
,
即,
,,
,
,
即,
,
、关于对称,
,,,
,
.
,
,
,
,
,
是以点为直角顶点的等腰直角三角形,
,
,
,
,
,
,
,
故AC,
在中,,
在中,,
,
,
,
,
故,
,
,
,,
,
,
,
即:的值为.
故答案为:.
连接,交于点,可设,,由直角三角形斜边上的中线的定义可得是有斜边上的中线,可得,,再由折叠的性质可得,,,从而可求得,则可证得是以点为直角顶点的等腰直角三角形,故有,从而可求得,再由,,得,可求得,,即可求解.
本题主要考查翻折变换折叠问题,解答的关键是明确折叠的过程中相应的边或角之间的关系.
14.【答案】
【解析】解:如图,连接.
在中,,,,
,
,
,
由对称的性质可知,,
,
的最小值为,
当点与重合时,的值最大,此时,,
.
故答案为:.
如图,连接求出,根据,推出的最小值为,当点与重合时,的值最大,求出的最大值,可得结论.
本题考查翻折变换,解直角三角形等知识,解题的关键是求出的最小值与最大值,属于中考常考题型.
15.【答案】
【解析】解:,,
.
,
,
.
在和中,
,
≌故正确;
≌,
.
又,
是的垂直平分线.
即垂直平分故正确;
取的中点,连接,
,,
.
,
.
,
.
,
.
.
,
即,故正确.
,
,
,
,
,
,
平分;故正确;
结论正确的是:.
故答案为:.
由条件可直接证得≌;由三角形全等的性质可得,又因为所以是的垂直平分线即垂直平分;取的中点连接,可得,再证明即可,即问题转化为证明≌再利用三角形的外角性质问题可得证.
本题考查了三角形全等的判断和性质;垂直平分线的判定;直角三角形斜边上的中线等于斜边的一半;等腰直角三角形两底角都是,题目难度不小,有一定的综合性.
16.【答案】
【解析】
【分析】
本题考查了三角形角平分线的性质 作,,根据角平分线性质知道,,,然后根据已知条件列式计算即可.
【解答】
解:作,,
在中,,
根据角平分线性质知道,,,
的周长,
又的周长,
的周长的周长,
四边形的周长,
四边形的周长,
,
.
故答案为.
17.【答案】答案
【解析】解析
18.【答案】解:如图所示:分别以直线、为对称轴,作点的对应点与,
连接交于,交于,
则最短.
【解析】分别以直线、为对称轴,作点的对应点与,连接交于,交于,则最短.
本题主要利用了两点之间线段最短的性质通过轴对称图形的性质确定三角形的另两点.
19.【答案】证明:点是的中点,,
,是等腰三角形,
,
,,
,
,
,
,
,
;
证明:点是的中点,,
是等腰三角形,
,
,
,
在和中,,
≌,
;
解:,点是的中点,
,
,
,
,
,
.
【解析】由线段垂直平分线的性质得,由等腰三角形的性质得,证,则,由和的内角和即可得出结论;
易证是等腰三角形,,得,由证得≌,即可得出结论;
由直角三角形的中线性质得,由求出,则,由,即可得出结果.
本题是三角形综合题,考查了全等三角形的判定与性质、线段垂直平分线的性质、三角形内角和定理、等腰三角形的判定与性质、等腰直角三角形的性质、直角三角形的中线性质、三角形面积的计算等知识;本题综合性强,熟练掌握等腰三角形的性质和全等三角形的判定与性质是解题的关键.
20.【答案】证明:为的角平分线,,,
,,
在和中,
≌,
,
点、都在的垂直平分线上,
垂直平分;
,
证明:为的角平分线,,
,
,
,,
,
,
.
【解析】根据角平分线的性质得到,证明≌,根据全等三角形的性质证明;
根据角平分线的定义、直角三角形的性质计算即可.
本题考查的是线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
21.【答案】解:如图,为所作;
是的垂直平分线,
,
的周长
.
【解析】利用基本作图作的垂直平分线;
根据线段垂直平分线的性质得到,然后利用等线段代换得到的周长,从而得到三角形的周长.
本题考查了作图基本作图:熟练掌握基本作图作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线也考查了线段垂直平分线的性质.
22.【答案】
【解析】证明:,
,
又,平分,
,
又,,
;
解:,
在与中,,
≌,
,
,,
,
的周长.
故答案为:.
根据角平分线的性质得到,等量代换即可得到结论;
根据全等三角形的性质得到,根据等腰直角三角形的性质得到,等量代换即可得到结论.
本题考查了全等三角形的判定与性质,等腰直角三角形的性质,角平分线的性质,熟练正确全等三角形的判定与性质是解题的关键.
23.【答案】证明:作于,于,如图,
在和中,
,为公共角,,
≌.
.
,
,
,,
,
由三角形面积公式得:,
,又,,
点在的平分线上.
【解析】首先证明≌,然后利用图形中的面积关系求得,已知,两三角形的底相等,所以它们的高也相等,它们的高即是,,所以点在的平分线上.
本题主要考查了角平分线上的点到角两边的距离相等的逆定理.而且考查了三角形全等判定和性质;所以学生所学的知识要系统.正确作出辅助线是解题的关键.
24.【答案】解:如图,结论:是的中线.理由如下:
是等边三角形,
,,
,
,
,
,
,
,
,
,,
,
是的中线.
结论:,理由如下:
如图,在上取,连接,
,,
为等边三角形,即,
,,
,
,
即,
,,
即,
在和,
,
≌,
,
,
.
,
如图,在上取,连接,,
为等边三角形,
,
是等边三角形,
,,
,
,
,
,
,
在和中,
,
≌
,
,,
,
,
,
,
.
【解析】本题属于三角形综合题,考查了全等三角形的判定与性质及等边三角形的判定与性质,解题的关键是正确作出辅助线,运用三角形全等找出对应的线段.
利用是等边三角形得出角,边关系,利用,,证明即可解决问题.
在上取,连接,利用≌得出,得出,
在上取,连接,,利用≌得出角的关系,得出是等腰三角形,根据边的关系得出结论.
25.【答案】
,;
证明:由知:≌,;
,
,
,
,
四边形是平行四边形,
,;
如图,中结论是否仍然成立,理由是:
延长交于点,
为等边三角形,
,,
,
在和中,
,
≌,
,,,
,
,
,
,
四边形是平行四边形,
,.
【解析】
解:是等边三角形,
,,
在和中,
,
≌,
,
;
故答案为:;
见答案;
见答案;
【分析】
证明≌,得,再由三角形外角的性质可得结论;
证明四边形是平行四边形,可得,;
同理证明≌和四边形是平行四边形,可得,.
此题是三角形的综合题,主要考查了等边三角形的性质,全等三角形的判定和性质,平行四边形的判定和性质,解题的关键是得出≌,并证明四边形是平行四边形,同理还运用了类比的方法解决问题.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
青岛版初中数学八年级上册第二单元《图形的轴对称》测试卷
考试范围:第二章;考试时间:120分钟;总分120分
学校:___________姓名:___________班级:___________考号:___________
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上,写在试卷上无效。
3.考试结束后,本试卷和答题卡一并交回。
第I卷(选择题)
一、选择题(本大题共12小题,共36分)
如图所示是一台球桌面的示意图,图中小正方形的边长均相等,黑球放在如图所示的位置,经白球撞击后沿箭头方向运动,经桌边反弹最后进入球洞的序号是( )
A. B. C. D.
在日常生活中,有一些含有特殊数字规律的车牌号码,如川,川,川等,这些牌照中的五个数字都是关于中间的一个数字“对称”的我们不妨把这样的牌照叫做数字对称牌照,如果让你负责制作以为字母“”后的第一个数字,且有五个数字的“数字对称”牌照,那么最多可制作( )
A. 个 B. 个 C. 个 D. 个
将一张长方形纸片如图进行折叠操作.第一次折叠后如图,使得,再沿着将纸片剪开,取部分继续折叠;第二次折叠后如图,使得,再沿着将纸片剪开,取部分继续折叠;按此操作,若将纸片沿着剪开,此时小于,则的最小值是( )
A. B. C. D.
将面积为的按图所示方式折叠,使点落在边上的点处,折痕为,若的面积为,则与的长度比为( )
A. B. C. D.
如图,已知和关于直线对称;如图,在射线上取点,连接,;如图,在射线上取点连接,,依此规律,第个图形中全等三角形的对数是( )
A. B. C. D.
下列说法正确的是( )
A. 等腰三角形的高线、中线、角平分线三线合一
B. 底角相等的两个等腰三角形全等
C. 角是轴对称图形,它的平分线是它的对称轴
D. 到三角形三个顶点距离相等的点是三角形三边垂直平分线的交点
在联谊会上,有、、三名选手站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在的( )
A. 三边中线的交点 B. 三条角平分线的交点
C. 三边中垂线的交点 D. 三边上高的交点
如图,在中,和的平分线,相交于点,交于,交于,过点作于,下列四个结论:;当时,;若,,则其中正确的是( )
A. B. C. D.
如图,中,、的角平分线、交于点,延长、,,,则下列结论中正确的个数( )
平分; ;;
A. 个 B. 个 C. 个 D. 个
等腰三角形的一个角是,则它的底角是( )
A. B. 或 C. 或 D.
如图,在菱形中,,的两顶点,分别落在边,上,从给出的四个条件中任选一个:;;;能够推出为等边三角形的是( )
A. B. C. D.
如图,,平分,且若点,分别在射线,上,且是边长为整数的等边三角形,则满足上述条件的点有参考数据: ( )
A. 个以上 B. 个 C. 个 D. 个
第II卷(非选择题)
二、填空题(本大题共4小题,共12分)
如图,已知中,,点是的中点,将沿所在的直线翻折,点落在点处,,且交于点,:的值为______.
如图,在中,,,,点为边的中点,点为边上一动点,连接,作关于直线的轴对称图形,点的对应点为点,连接,则长度的取值范围为______.
在四边形中,,,,为上一点,,且,的延长线于连接交对角线于下列结论:≌;垂直平分;;平分其中结论正确的是______填序号
如图,在中,,与的平分线交于点,于点若与的周长差为,四边形的周长为,则等于________.
三、解答题(本大题共9小题,共72分)
某货运公司最近接了一批货物,决定采用厢式货车托运甲、乙两种货物,已知某辆厢式货车所装托运货物的总体积不能超过,总重量不能超过甲、乙两种货物每袋的体积单位:、重量单位:和可获得的利润单位:元列表如下:
货物 每袋体积 每袋重量 每袋利润
甲
乙
问该辆厢式货车托运这两种货物各多少袋时,可获得最大利润?
如图,内有一点,在射线上找出一点,在射线上找出一点,使最短.
已知:在四边形中,,相交于点,且点是的中点,,过点作,垂足为点,与交于点.
如图,求证:;
如图,若;
求证:;
若,的面积为,求四边形的面积.
如图,为的角平分线,于点,于点,连接交于点.
求证:垂直平分;
若,写出与之间的数量关系,不需证明.
如图,中
尺规作图:作的垂直平分线,交于点,交于点 .
在图中连,如果,,求的周长.
如图,在中,,平分,交于点,.
求证:;
若,则的周长为______.
如图,在的两边,上分别取,,和相交于点.
求证:点在的平分线上.
已知:为等边三角形,点为射线上一点,点为射线上一点,.
如图,当在的延长线上且时,是的中线吗?请说明理由;
如图,当在的延长线上时,等于吗?请说明理由;
如图,当在线段的延长线上,在线段上时,请直接写出、、的数量关系.
已知为等边三角形,点、分别在直线、上,且.
如图,若点、分别是、边上的点,连接、交于点,过点作,使,连接,则______填度数;
在的条件下,猜想与存在什么关系,并证明;
如图,若点、分别是、延长线上的点,中结论是否仍然成立?请给出判断并证明.
答案和解析
1.【答案】
【解析】
【分析】
本题主要考查了生活中的轴对称现象;结合轴对称的知识画出图形是解答本题的关键.入射光线与水平线的夹角等于反射光线与水平线的夹角,动手操作即可.
【解答】
解:如图,求最后落入球洞;
故选A.
2.【答案】
【解析】解:以为字母“”后的第一个数字且有五个数字的“数字对称”牌照,
第一位为,则第五个也是
第三位可以是中任意一个,有种可能.
第二、第四位可以是中任意一个,有种可能.
所以开头的组合最多是个.
故选C.
以开头,那么最后一位数字也只能是,那么只有中间位可以随便取,又因为第二位和第四位数字必须一样,实际上只有第二位和第三位可以取十个数字,所以只有个.
本题考查了轴对称图形的知识,注意掌握对称的要求,正确分析各个数位的数字情况.
3.【答案】
【解析】
【分析】
本题考查了图形折叠的规律问题,由题意找出规律,列出不等式解出即可.
【解答】
解:由题意得:第一次折叠后,
第一次折叠后,
第次折叠后,
所以,
则的最小值为,
故选C.
4.【答案】
【解析】
【分析】
本题考查了折叠的性质:折叠前后的两个三角形是全等三角形,它们的面积相等.由题意分别计算出与的面积,从而::,问题可解.
【解答】
解:由题意可得:
由折叠性质可知,,
::::.
故选A.
5.【答案】
【解析】
【分析】
此题主要考查了三角形全等的判定以及规律的归纳,解题的关键是根据条件证出图形中有几对三角形全等,然后寻找规律.
根据条件可得图中有对三角形全等;图中可证出,,有对三角形全等;图中有对三角形全等,根据数据可分析出第个图形中全等三角形的对数.
【解答】
解:和关于直线对称,
.
在与中
,
.
图中有对三角形全等;
同理图中,,
,
,
,
在和中
,
,
图中有对三角形全等;
同理:图中有对三角形全等;
由此发现:第个图形中全等三角形的对数是.
故选:.
6.【答案】
【解析】
【分析】
本题主要考查了等腰三角形的性质,全等三角形的判定,轴对称图形的定义,线段垂直平分线的性质,关键是结合各个知识点对各个选项依次判断.
【解答】
解:等腰三角形底边上的高线、中线,顶角的平分线三线合一,故本项错误;
B.底角相等的两个等腰三角形,即两个等腰三角形的三个角对应相等,这两个三角形不一定全等,故本项错误;
C.角是轴对称图形,它的平分线所在直线是它的对称轴,故本项错误;
D.三角形三个顶点距离相等的点是三角形三边垂直平分线的交点,故本项正确;
故选D.
7.【答案】
【解析】解:三角形的三条垂直平分线的交点到三角形各顶点的距离相等,
凳子应放在的三条垂直平分线的交点最适当.
故选:.
为使游戏公平,要使凳子到三个人的距离相等,于是利用线段垂直平分线上的点到线段两端的距离相等可知,要放在三边中垂线的交点上.
本题主要考查了线段垂直平分线的性质的应用;利用所学的数学知识解决实际问题是一种能力,要注意培养.想到要使凳子到三个人的距离相等是正确解答本题的关键.
8.【答案】
【解析】解:和的平分线相交于点,
,,
,正确;
,
,
,分别是与的平分线,
,
,
,
,
如图,在上取一点,使,
是的角平分线,
,
在和中,,
≌,
,
,
,
在和中,,
≌,
,
,故正确;
作于,于,
和的平分线相交于点,
点在的平分线上,
,
,正确.
故选:.
由角平分线的定义结合三角形的内角和的可求解与的关系,进而判定;在上取一点,使,证得≌,得到,再证得≌,得到,进而判定正确;作于,于,根据三角形的面积可证得正确.
本题主要考查了三角形内角和定理,三角形外角的性质,三角形全等的性质和判定,正确作出辅助线证得≌,得到,是解决问题的关键.
9.【答案】
【解析】
【分析】
本题考查了角平分线的性质与判定,全等三角形的判定与性质,三角形的外角性质,掌握角平分线的性质判定是解题的关键.
作于,由角平分线的性质得出,,得出,即可得出正确;
首先证出,证明≌,得出,同理:≌,得出,即可得出正确;
由角平分线和三角形的外角性质得出,,得出,即可得出正确;
由全等三角形的性质得出,,即可得出正确.
【解答】
解:作于,
平分,平分,,,
,,
,
点在的角平分线上,故正确;
,,
,
,
在和中,
,
≌,
,
同理:≌,
,
,
,正确;
平分,平分,
,,
,正确;
≌,
,
同理:≌,
,
,正确;
故选:.
10.【答案】
【解析】解:当底角为时,则底角为,
当顶角为时,由三角形内角和定理可求得底角为:,
所以底角为或,
故选:.
分这个角为底角和顶角两种情况讨论即可.
本题主要考查等腰三角形的性质,分两种情况讨论是解题的关键.
11.【答案】
【解析】
【分析】
本题考查等边三角形的判定与性质.
根据等边三角形的判定方法分别对四个条件一一推理判断即可.
【解答】
解:能够推出为等边三角形
理由如下:
如图
四边形是菱形,
,
和都是等边三角形,
,
,
在和中,
,
,
为等边三角形.
能够推出为等边三角形
理由如下:
如图
四边形是菱形,
.
.
是等边三角形,
在上截取,则是等边三角形,
,
,又因为,
.
在与中,
.
,
.
,
是等边三角形
不能推出为等边三角形
理由如下:
如图
四边形是菱形,
,
和都是等边三角形,
,,
因为,,,边边角不能判定与全等,
故不能推出为等边三角形;
不能推出为等边三角形
理由如下:
如图
在上截取,
四边形是菱形,
,
、和都是等边三角形,
,
,
因为,,,边边角不能判定与全等,
故不能推出为等边三角形.
12.【答案】
【解析】
【分析】
本题考等边三角形判定和性质、全等三角形的判和性质、角平分线的定义,勾股定理.解的关键是添加辅助线,构造等边三角形,由此即可得出结论.
【解答】
解:在、上截取,作.
平分,
,是等边角形,
,,
,
在和中,
,
,
,
是等边三角形,
当时,,
边长为整数,,分别在射线,上,
的整数,
或,
这样的整数只有和,两边各有两个满足条件的三角形,即满足上述条件的点有个.
故选B.
13.【答案】
【解析】解:连接,交于点,如图,
设,,
是的中点,,
是有斜边上的中线,
,
即,
,,
,
,
即,
,
、关于对称,
,,,
,
.
,
,
,
,
,
是以点为直角顶点的等腰直角三角形,
,
,
,
,
,
,
,
故AC,
在中,,
在中,,
,
,
,
,
故,
,
,
,,
,
,
,
即:的值为.
故答案为:.
连接,交于点,可设,,由直角三角形斜边上的中线的定义可得是有斜边上的中线,可得,,再由折叠的性质可得,,,从而可求得,则可证得是以点为直角顶点的等腰直角三角形,故有,从而可求得,再由,,得,可求得,,即可求解.
本题主要考查翻折变换折叠问题,解答的关键是明确折叠的过程中相应的边或角之间的关系.
14.【答案】
【解析】解:如图,连接.
在中,,,,
,
,
,
由对称的性质可知,,
,
的最小值为,
当点与重合时,的值最大,此时,,
.
故答案为:.
如图,连接求出,根据,推出的最小值为,当点与重合时,的值最大,求出的最大值,可得结论.
本题考查翻折变换,解直角三角形等知识,解题的关键是求出的最小值与最大值,属于中考常考题型.
15.【答案】
【解析】解:,,
.
,
,
.
在和中,
,
≌故正确;
≌,
.
又,
是的垂直平分线.
即垂直平分故正确;
取的中点,连接,
,,
.
,
.
,
.
,
.
.
,
即,故正确.
,
,
,
,
,
,
平分;故正确;
结论正确的是:.
故答案为:.
由条件可直接证得≌;由三角形全等的性质可得,又因为所以是的垂直平分线即垂直平分;取的中点连接,可得,再证明即可,即问题转化为证明≌再利用三角形的外角性质问题可得证.
本题考查了三角形全等的判断和性质;垂直平分线的判定;直角三角形斜边上的中线等于斜边的一半;等腰直角三角形两底角都是,题目难度不小,有一定的综合性.
16.【答案】
【解析】
【分析】
本题考查了三角形角平分线的性质 作,,根据角平分线性质知道,,,然后根据已知条件列式计算即可.
【解答】
解:作,,
在中,,
根据角平分线性质知道,,,
的周长,
又的周长,
的周长的周长,
四边形的周长,
四边形的周长,
,
.
故答案为.
17.【答案】答案
【解析】解析
18.【答案】解:如图所示:分别以直线、为对称轴,作点的对应点与,
连接交于,交于,
则最短.
【解析】分别以直线、为对称轴,作点的对应点与,连接交于,交于,则最短.
本题主要利用了两点之间线段最短的性质通过轴对称图形的性质确定三角形的另两点.
19.【答案】证明:点是的中点,,
,是等腰三角形,
,
,,
,
,
,
,
,
;
证明:点是的中点,,
是等腰三角形,
,
,
,
在和中,,
≌,
;
解:,点是的中点,
,
,
,
,
,
.
【解析】由线段垂直平分线的性质得,由等腰三角形的性质得,证,则,由和的内角和即可得出结论;
易证是等腰三角形,,得,由证得≌,即可得出结论;
由直角三角形的中线性质得,由求出,则,由,即可得出结果.
本题是三角形综合题,考查了全等三角形的判定与性质、线段垂直平分线的性质、三角形内角和定理、等腰三角形的判定与性质、等腰直角三角形的性质、直角三角形的中线性质、三角形面积的计算等知识;本题综合性强,熟练掌握等腰三角形的性质和全等三角形的判定与性质是解题的关键.
20.【答案】证明:为的角平分线,,,
,,
在和中,
≌,
,
点、都在的垂直平分线上,
垂直平分;
,
证明:为的角平分线,,
,
,
,,
,
,
.
【解析】根据角平分线的性质得到,证明≌,根据全等三角形的性质证明;
根据角平分线的定义、直角三角形的性质计算即可.
本题考查的是线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
21.【答案】解:如图,为所作;
是的垂直平分线,
,
的周长
.
【解析】利用基本作图作的垂直平分线;
根据线段垂直平分线的性质得到,然后利用等线段代换得到的周长,从而得到三角形的周长.
本题考查了作图基本作图:熟练掌握基本作图作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线也考查了线段垂直平分线的性质.
22.【答案】
【解析】证明:,
,
又,平分,
,
又,,
;
解:,
在与中,,
≌,
,
,,
,
的周长.
故答案为:.
根据角平分线的性质得到,等量代换即可得到结论;
根据全等三角形的性质得到,根据等腰直角三角形的性质得到,等量代换即可得到结论.
本题考查了全等三角形的判定与性质,等腰直角三角形的性质,角平分线的性质,熟练正确全等三角形的判定与性质是解题的关键.
23.【答案】证明:作于,于,如图,
在和中,
,为公共角,,
≌.
.
,
,
,,
,
由三角形面积公式得:,
,又,,
点在的平分线上.
【解析】首先证明≌,然后利用图形中的面积关系求得,已知,两三角形的底相等,所以它们的高也相等,它们的高即是,,所以点在的平分线上.
本题主要考查了角平分线上的点到角两边的距离相等的逆定理.而且考查了三角形全等判定和性质;所以学生所学的知识要系统.正确作出辅助线是解题的关键.
24.【答案】解:如图,结论:是的中线.理由如下:
是等边三角形,
,,
,
,
,
,
,
,
,
,,
,
是的中线.
结论:,理由如下:
如图,在上取,连接,
,,
为等边三角形,即,
,,
,
,
即,
,,
即,
在和,
,
≌,
,
,
.
,
如图,在上取,连接,,
为等边三角形,
,
是等边三角形,
,,
,
,
,
,
,
在和中,
,
≌
,
,,
,
,
,
,
.
【解析】本题属于三角形综合题,考查了全等三角形的判定与性质及等边三角形的判定与性质,解题的关键是正确作出辅助线,运用三角形全等找出对应的线段.
利用是等边三角形得出角,边关系,利用,,证明即可解决问题.
在上取,连接,利用≌得出,得出,
在上取,连接,,利用≌得出角的关系,得出是等腰三角形,根据边的关系得出结论.
25.【答案】
,;
证明:由知:≌,;
,
,
,
,
四边形是平行四边形,
,;
如图,中结论是否仍然成立,理由是:
延长交于点,
为等边三角形,
,,
,
在和中,
,
≌,
,,,
,
,
,
,
四边形是平行四边形,
,.
【解析】
解:是等边三角形,
,,
在和中,
,
≌,
,
;
故答案为:;
见答案;
见答案;
【分析】
证明≌,得,再由三角形外角的性质可得结论;
证明四边形是平行四边形,可得,;
同理证明≌和四边形是平行四边形,可得,.
此题是三角形的综合题,主要考查了等边三角形的性质,全等三角形的判定和性质,平行四边形的判定和性质,解题的关键是得出≌,并证明四边形是平行四边形,同理还运用了类比的方法解决问题.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
