人教A版2019选择性必修第三册6.1.2 两个计数原理的综合应用 学案(Word版含答案)
文档属性
| 名称 | 人教A版2019选择性必修第三册6.1.2 两个计数原理的综合应用 学案(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-29 15:44:37 | ||
图片预览




文档简介
6.1.2两个计数原理的综合应用
【考点梳理】
知识点一 两个计数原理的区别与联系
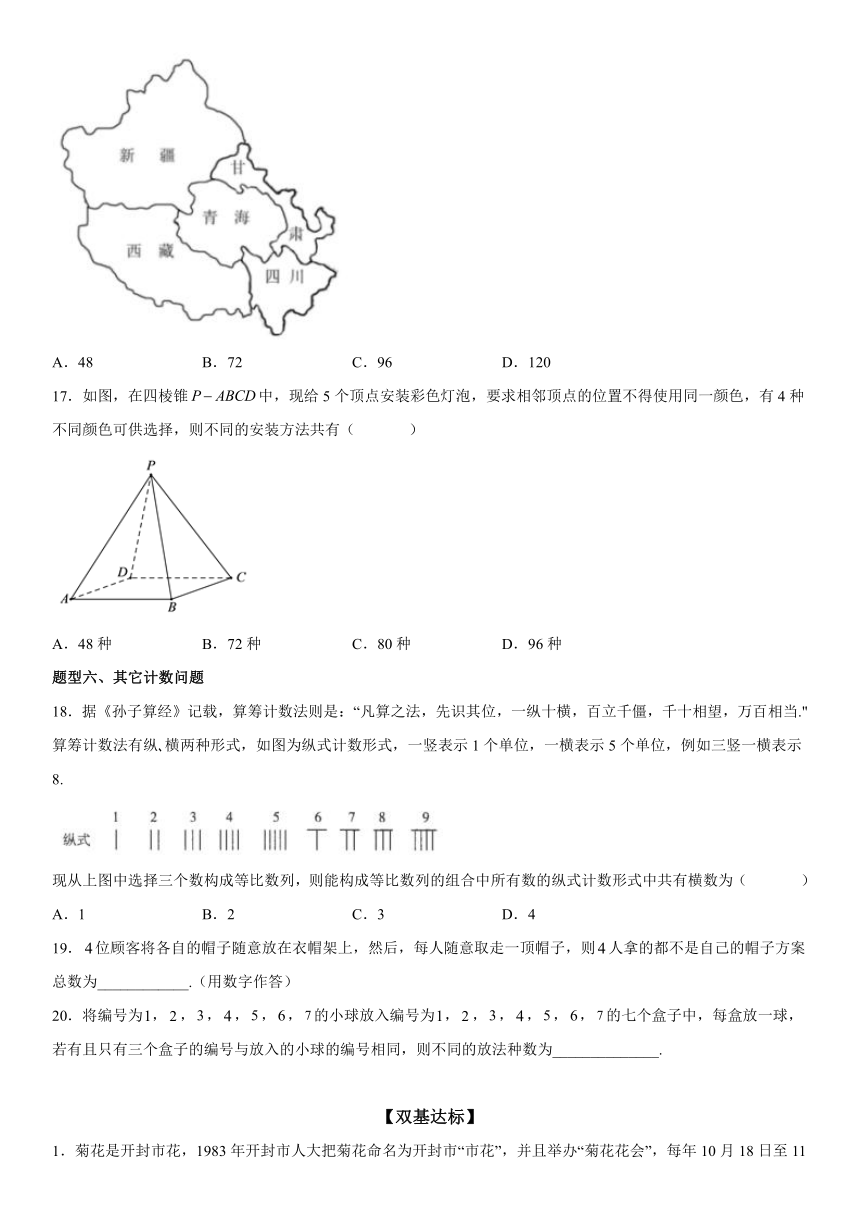
分类加法计数原理 分步乘法计数原理
相同点 回答的都是有关做一件事的不同方法种数的问题
不同点 针对的是“分类”问题
不同点 各种方法相互独立,用其中任何一种方法都可以做完这件事 各个步骤中的方法互相依存,只有每一个步骤都完成才算做完这件事
知识点二 两个计数原理的应用
用两个计数原理解决计数问题时,最重要的是在开始计算之前要仔细分析两点:
一、要完成的“一件事”是什么;二、需要分类还是需要分步.
(1)分类要做到“不重不漏”,分类后再分别对每一类进行计数,最后用分类加法计数原理求和,得到总数.
(2)分步要做到“步骤完整”,即完成了所有步骤,恰好完成任务.分类后再计算每一步的方法数,最后根据分步乘法计数原理,把完成每一步的方法数相乘,得到总数.
【题型归纳】
题型一、实际问题中的计数问题
1.甲与其四位同事各有一辆私家车,车牌尾数分别是9,0,2,1,5,为遵守当地某月5日至9日5天的限行规定(奇数日车牌尾数为奇数的车通行,偶数日车牌尾数为偶数的车通行),五人商议拼车出行,每天任选一辆符合规定的车,但甲的车最多只能用一天,则不同的用车方案种数为( )
A.64 B.80 C.96 D.120
2.在填写高考志愿表时,一名高中毕业生了解到,A,B两所大学各有一些自己感兴趣的强项专业,如表:
A大学 B大学
生物学 数学
化学 会计学
医学 信息技术学
二物理学 法学
工程学
如果这名同学只能选一个专业,那么他共有多少种选择?
3.计算机编程人员在编写好程序以后需要对程序进行测试.程序员需要知道到底有多少条执行路径(即程序从开始到结束的路线),以便知道需要提供多少个测试数据.一般地,一个程序模块由许多子模块组成.如图,这是一个具有许多执行路径的程序模块,它有多少条执行路径?另外,为了减少测试时间,程序员需要设法减少测试次数.你能帮助程序员设计一个测试方法,以减少测试次数吗?
题型二、代数中的计数问题
4.甲 乙两人做从装有14个玻璃球的盒子中抓取玻璃球的游戏,规定:甲 乙两人轮流抓取,每次至少抓取1个,最多抓取4个,最后一次取完者获胜.若甲先抓取,为确保甲一定获胜,则甲第一次应该抓取的玻璃球个数为( )
A.1 B.2 C.3 D.4
5.集合,满足,,若,中的元素个数分别不是,中的元素,则满足条件的集合的个数为____.(用数字作答)
6.从1,2,3,4,7,9六个数中,任取两个数作为对数的底数和真数,则所有不同的对数值的个数为____.
7.已知集合M∈{1,-2,3),N∈{-4,5,6,-7},从两个集合中各取一个元素作为点的坐标,则这样的坐标在直角坐标系中可表示第一、二象限内不同的点的个数是( )
A.18 B.10 C.16 D.14
题型三、几何计数问题
8.一个国际象棋棋盘(由8×8个方格组成),其中有一个小方格因破损而被剪去(破损位置不确定).“L”形骨牌由三个相邻的小方格组成,如图所示.现要将这个破损的棋盘剪成数个“L”形骨牌,则( )
A.至多能剪成19块“L”形骨牌
B.至多能剪成20块“L”形骨牌
C.最多能剪成21块“L”形骨牌
D.前三个答案都不对
9.以三棱柱的顶点为顶点共可组成________个不同的三棱锥?
10.在如图所示的的方格纸上(每个小方格均为正方形),共有________个矩形、________个正方形.
题型四、数字排列问题
11.用数字、、组成五位数,且数字、、至少都出现一次,这样的五位数共有( )个
A. B. C. D.
12.由数字0,1,2,3,4,5组成没有重复数字的六位数,其中个位数字小于十位数字的共有( )
A.210个 B.300个
C.464个 D.600个
13.从、、、这个数字中选出个不同的数字组成个三位数,试写出所有满足条件的三位数.
14.“回文数”是指从左到右读与从右到左读都一样的正整数.如22,121,343,94249等.显然,2位数的回文数有9个,即11,22,33,…,99;3位数的回文数有90个:101,111,121,…,191,202,…,999.求:
(1)4位数的回文数个数;
(2)位数的回文数个数.
题型五、涂色问题
15.将红、黄、绿三种不同的颜色均涂入图中五个区域中,每个区域涂一种颜色,且相邻的区域不能涂同一种颜色,不同的涂色方法共有__种.(三种颜色必须用全,以数字作答)
16.在中国地图上,西部五省(甘肃、四川、青海、新疆、西藏)如图所示,有四种颜色供选择,要求每省涂一色,相邻省不同色,则不同的涂色方法有( )种.
A.48 B.72 C.96 D.120
17.如图,在四棱锥中,现给5个顶点安装彩色灯泡,要求相邻顶点的位置不得使用同一颜色,有4种不同颜色可供选择,则不同的安装方法共有( )
A.48种 B.72种 C.80种 D.96种
题型六、其它计数问题
18.据《孙子算经》记载,算筹计数法则是:“凡算之法,先识其位,一纵十横,百立千僵,千十相望,万百相当."算筹计数法有纵 横两种形式,如图为纵式计数形式,一竖表示1个单位,一横表示5个单位,例如三竖一横表示8.
现从上图中选择三个数构成等比数列,则能构成等比数列的组合中所有数的纵式计数形式中共有横数为( )
A.1 B.2 C.3 D.4
19.位顾客将各自的帽子随意放在衣帽架上,然后,每人随意取走一顶帽子,则人拿的都不是自己的帽子方案总数为____________.(用数字作答)
20.将编号为,,,,,,的小球放入编号为,,,,,,的七个盒子中,每盒放一球,若有且只有三个盒子的编号与放入的小球的编号相同,则不同的放法种数为______________.
【双基达标】
1.菊花是开封市花,1983年开封市人大把菊花命名为开封市“市花”,并且举办“菊花花会”,每年10月18日至11月18日为“菊花花会”的会期.如图是某展区的一个菊花布局图,现有5个不同品种的菊花可供选择,要求相邻的两个展区不使用同一种菊花,则不同的布置方法有( )
A.种 B.种 C.种 D.种
2.埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,如图,将一个四棱锥的每一个顶点染上一种颜色,并使同一条棱上的两端异色,如果只有5种颜色可供使用,则不同的染色方法总数为( )
A. B. C. D.
3.为了支援山区教育,现在安排名大学生到个学校进行支教活动,每个学校至少安排人,其中甲校至少要安排名大学生,则不同的安排方法共有( )种
A. B. C. D.
4.从1,2,3,4,5,6,7,8,9这9个数字中任取两个,其中一个作为底数,另一个作为真数,则可以得到不同对数值的个数为( )
A.64 B.56 C.53 D.51
5.如果一个三位正整数如“”满足且,则称这个三位数为“凸数”(如120,343,275等),那么所有三位数中“凸数”的个数为______.
6.小明有4枚完全相同的硬币,每个硬币都分正反两面.他想把4个硬币摆成一摞,且满足相邻两枚硬币的正面与正面不相对,不同的摆法有________种.
7.某班一天上午有4节课,每节都需要安排一名教师去上课,现从,,,,,6名教师中安排4人分别上一节课,第一节课只能从,两人中安排一人,第四节课只能从,两人中安排一人,则不同的安排方案共有______种.(用数字作答)
8.(1)某外语组有9人,每人至少会英语和日语中的一门,其中7人会英语,3人会日语,从中选出会英语和日语的各一人,有______种不同的选法;
(2)将4封信投入3个信箱中,共有______种不同的投法.
9.如图所示的,,,按照下列要求涂色.
(1)用3种不同颜色填涂图中,,,四个区域,且使相邻区域不同色,若按从左到右依次涂色,有多少种不同的涂色方案?
(2)若恰好用3种不同颜色给,,,四个区域涂色,且相邻区域不同色,共有多少种不同的涂色方案?
(3)若有3种不同颜色,恰好用2种不同颜色涂完四个区域,且相邻区域不同色,共有多少种不同的涂色方案?
10.用1、2、3、4、5、6、7这7个数字组成没有重复数字的四位数.
(1)这些四位数中偶数有多少个 能被5整除的有多少个
(2)这些四位数中大于6 500的有多少个
【高分突破】
1.如果正整数a的各位数字之和等于6,那么称a为“好数”(如:6,24,2013等均为“好数”),将所有“好数”从小到大排成一列a1,a2,a3,…,若an=2 013,则n=( )
A.50 B.51 C.52 D.53
2.四色定理(Four color theorem)又称四色猜想,是世界近代三大数学难题之一.它是于1852年由毕业于伦敦大学的格斯里(Francis Guthrie)提出来的,其内容是“任何一张地图只用四种颜色就能使具有共同边界的国家着上不同的颜色.”四色问题的证明进程缓慢,直到1976年,美国数学家运用电子计算机证明了四色定理.现某校数学兴趣小组给一个底面边长互不相等的直四棱柱容器的侧面和下底面染色,提出如下的“四色问题”:要求相邻两个面不得使用同一种颜色,现有4种颜色可供选择,则不同的染色方案有( )
A.18种 B.36种 C.48种 D.72种
3.如图为我国数学家赵爽在为《周髀算经》作注时验证勾股定理的示意图,现提供5种颜色给其中5个小区域,,,,涂色,规定每个区域只涂1种颜色,相邻区域颜色不相同,则不同的涂色方案共有______种.
4.某外语组9人,每人至少会英语和日语中的一门,其中7人会英语,3人会日语,从中选出会英语和日语的各一人,则不同的选法有________种.
5.若某四位数满足,则称该四位数为“收敛四位数”,则所有“收敛四位数”的个数是______.(用数字作答)
6.有标号为1,2,3,4,5,6的6个小球和标号为1,2,3,4的4个盒.
(1)从6个小球中选出4个放入4个盒中,每盒只放1个小球.
①求奇数号盒只放奇数号小球的不同放法种数;
②求奇数号小球必须放在奇数号盒中的不同放法种数.
(2)若不许空盒且将6个小球都放入4个盒中,求所有不同的放法种数.
7.用种不同的颜色给如图所示的、、、四个区域涂色.
(1)若相邻区域能用同一种颜色,则图①有多少种不同的涂色方案?
(2)若相邻区域不能用同一种颜色,当时,图①、图②各有多少种不同的涂色方案?
(3)若相邻区域不能用同一种颜色,图③有种不同的涂色方案,求的值.
8.用0,1,2,3,4,5这六个数字可以组成多少个无重复数字的
(1)能被5整除的五位数;
(2)能被3整除的五位数;
(3)若所有的六位数按从小到大的顺序组成一个数列{an},则240 135是第几项.
9.已知集合A={2,4,6,8},B={1,3,5,7,9},从A中取一个数作为十位数字,从B中取一个数作为个位数字,问:
(1)能组成多少个不同的两位数?
(2)能组成多少个十位数字小于个位数字的两位数?
【答案详解】
【题型归纳】
1.B
【详解】5日至9日,日期尾数分别为5,6,7,8,9,有3天是奇数日,2天是偶数日.第一步,安排偶数日出行,每天都有2种选择,共有2×2=4(种);第二步,安排奇数日出行,分两类,第一类,选1天安排甲的车,另外2天安排其他车,有3×2×2=12(种),第二类,不安排甲的车,每天都有2种选择,共有=8(种),共有12+8=20(种).根据分步乘法计数原理,不同的用车方案种数为4×20=80.
故选:B.
2.9.
【详解】这名同学可以选择A,B两所大学中的一所.在A大学中有5种专业选择方法,在B大学中有4种专业选择方法,∵没有一个强项专业是两所大学共有的,∴根据分类加法计数原理,这名同学可能的专业选择种数.
3.7371.
【详解】由分类加法计数原理,子模块1、子模块2、子模块3中的子路径条数共为
;
子模块4、子模块5中的子路径条数共为,
又由分步乘法计数原理,整个模块的执行路径条数共为;
在实际测试中,程序员总是把每一个子模块看成一个黑箱,
即通过只考察是否执行了正确的子模块的方式来测试整个模块,
这样,他可以先分别单独测试5个模块,以考察每个子模块的工作是否正常,
总共需要的测试次数为,
再测试各个模块之间的信息交流是否正常,
只需要测试程序第1步中的各个子模块和第2步中的各个子模块之间的信息交流是否正常,
需要的测试次数为,
如果每个子模块都工作正常,并且各个子模块之间的信息交流也正常,那么整个程序模块就工作正常,
这样,测试整个模块的次数就变为,
显然,178与7371的差距是非常大的,故用以上测试方法,可以减少测试次数.
4.D
【详解】因为每人每次至少抓取1个,最多抓取4个
当两人所拿的和为5时,有
所以甲第一次应该抓取4个玻璃球,后面只要满足甲拿的球与乙拿的球和为5,则甲一定获胜
故选:D
5.44.
【详解】含1元,含7元,则,,于是,,共;同理:含2元,含6元,共6个;含3元,含5元,共15个;含5元,含3元,共15个;含6元,含2元,共6个;含7元,含1元,共1个.
6.17
【详解】
①当取得两个数中有一个是1时,则1只能作真数,此时loga1=0,a=2或3或4或7或9.
②所取的两个数不含有1时,即从2,3,4,7,9中任取两个,分别作为底数与真数可有=20个对数,但是其中,
.
综上可知:共可以得到20+1﹣4=17个不同的对数值.
故答案为17.
点睛:本题是一道易错题,防止重复,其中,
,处理计数原理问题,贵在不重不漏,需要同学们熟练掌握对数的运算法则.
7.D
【详解】M中的元素作点的横坐标,N中的元素作点的纵坐标,
在第一象限的点共有2×2个,在第二象限的点共有1×2个.
N中的元素作点的横坐标,M中的元素作点的纵坐标,
在第一象限的点共有2×2个,在第二象限的点共有2×2个.
所求不同的点的个数是2×2+1×2+2×2+2×2=14(个).
故选:D.
8.C
【详解】考虑2×3的6块方格,如图:,每一块这样的骨牌含有2块“L”形骨牌
一共可以剪成10块这样的骨牌,和一个田字格,田字格可以剪1块“L”形骨牌,则一共21块“L”形骨牌.
只要将破损的方格所在位置剪成一个恰当的田字格即可,所以一定能够剪成21块“L”形骨牌.
如图所示
故选:C
9.12
【详解】从个顶点中选出个的方法数有种,其中共面的有种(即个侧面),故可以构成不同三棱锥的方法数有种.
44. 280 60
10.【详解】根据题意,7×4的方格纸上,有5条水平方向的线,8条竖直方向的线,
在5条水平方向的线中任选2条,在8条竖直方向的线中任选2条,就可以组成一个矩形,
则可以组成个矩形;
设方格纸上的小方格的边长为1,
当正方形的边长为1时,有7×4=28个正方形,
当正方形的边长为2时,有6×3=18个正方形,
当正方形的边长为3时,有5×2=10个正方形,
当正方形的边长为4时,有4×1=4个正方形,
则有28+18+10+4=60个正方形;
故答案为:280,60.
11.B
【详解】首先考虑全部的情况,即每个数位均有种选择,共有个,
其中包含数字全部相同只有种情况,
还有只含有个数字的共有个,
因此,满足条件的五位数的个数为个.
故选:B.
12.B
【详解】由题意得,个位数字小于十位数字,
所以个位数字只能是0,1,2,3,4共5种类型,
每种类型分别有个,
共有
故选:B
13.【详解】所有满足条件的三位数分别为:、、、、、、、、、、、、、、、、、,共个.
14.(1)90
(2)
【详解】(1)由题设,四位数回文:
∴共有90个.
(2)位数,则中间的数字有10种选法,而两侧的数字只需排好一侧,则另一侧确定,
不妨排前n位数字,显然第一位数字有9种选法,其余都有10种选法,
∴共有个回文数.
15.42
【详解】由题意,不妨从左至右按编号,由于三种颜色必须用全,第一步涂一号有三种涂法,第二步涂二号有二种涂法第三步涂三号时可分为两类研究,若三号与一号同则后两框必一框涂色与一号二号不同,与若三号与一号不同,由于三种颜色已全部用上,故后两框涂色只需要满足同色不相邻即可,
故总的涂色方法为种
故答案为:42.
16.B
【详解】先进行编号:新疆、甘肃、青海、西藏、四川,
按的顺序进行涂色,其中颜色可以相同或不相同,
所以不同的涂色方法数有种.
故选:B
17.B
【详解】若A,C使用同一颜色,则由分步计数原理可知有(种);
若A,C不使用同一颜色,则由分步计数原理可知有(种),
由分类计数原理可得共有(种),
故选:B.
18.D
【详解】正整数1~9中能构成等比数列的三个数一共有四组,分别是1,2,4;2,4,8;1,3,9;4,6,9.
其中只有6,8,9的纵式计数形式中各有1横,所以共有4横
故选:D
19.
【详解】记位顾客分别为甲、乙、丙、丁.
假设甲拿了乙的帽子,则乙拿了甲的帽子,丙拿了丁的帽子,丁拿了丙的帽子;或乙拿丙的帽子,丙拿了丁的帽子,丁拿了甲的帽子;或乙拿了丁的帽子,丙拿了甲的帽子,丁拿了丙的帽子.
若甲拿了丙或丁的帽子,同理可知,符合条件的方案数均为种.
综上所述,人拿的都不是自己的帽子方案总数为.
故答案为:.
20.
【详解】按两步进行计算:
1. 选出盒子的编号与小球编号相同的3个编号,共有种选法;
2.对余下的4个编号的球,将它们放置到不同盒子中,且盒子的编号与球的编号不同,有种方法,
故不同的放法种数为,
故答案为:
【双基达标】
1.D
【详解】先布置中心区域共有种方法,从开始沿逆时针方向进行布置四周的区域,则有种布置方法,有种布置方法.
如果与选用同一种菊花,则有种布置方法;如果与选用不同种类菊花,则有种布置方法,有种布置方法.按照分步乘法与分类加法计数原理,
则全部的布置方法有(种),
故选:.
2.C
【详解】分两步,先将四棱锥一侧面三顶点染色,然后再分类考虑另外两顶点的染色数,用乘法原理可求解,由题设,四棱锥S - ABCD的顶点S, A, B所染的颜色互不相同,它们共有种染色方法;
当染好时,不妨设所染颜色依次为1, 2, 3,若C染2,则D可染3或4或5,有3种染法;若C染4,则D可染3或5,有2种染法;若C染5,则D可染3或4,有2种染法,即当S, A, B染好时,C, D还有7种染法.
故不同的染色方法有种.
故选:C
3.C
【详解】若甲校分名大学生,此时有种分配方法;
若甲校分名大学生,此时有种分配方法.
综上所述,共有种分配方法.
故选:C.
4.C
【详解】由于1只能作为真数,则以1为真数,从其余各数中任取一数为底数,对数值均为0,
从除1外的其余各数中任取两数分别作为对数的底数和真数,共能组成个对数式,
其中,,,,,重复了4次,
所以得到不同对数值的个数为.
故选:C
5.240
【详解】若,则“凸数”为120与121,共有(个);
若,则“凸数”有(个);
若,则“凸数”有(个);
若,则“凸数”有(个);
若,则“凸数”有(个);
若,则“凸数”有(个);
若,则“凸数”有(个);
若,则“凸数”有(个).
所以所有三位数中“凸数”的个数为.
故答案为:240.
6.5
【详解】
记反面为1,正面为2,则正反依次相对有12121212,21212121两种;有两枚反面相对有21121212,21211212,21212112三种,共5种摆法.
故答案为:5.
7.36
【详解】不同的安排方案有两类办法:
第一类,第一节课若安排,则第四节课只能安排,第二节课从剩余4人中任选1人,第三节课从剩余3人中任选1人,共有种排法;
第二类,第一节课若安排,则第四节课可安排或,第二节课从剩余4人中任选1人,第三节课从剩余3人中任选1人,共有种排法,
因此不同的安排方案有种.
故答案为:36
8. 20 81
【详解】(1)共分三类:第一类,当选出的会英语的人既会英语又会日语时,选会日语的人有2种选法;
第二类,当选出的会日语的人既会英语又会日语时,选会英语的人有6种选法;
第三类,当既会英语又会日语的人不参与选择时,则需从只会日语和只会英语的人中各选一人,有(种)选法.
故共有(种)选法.
(2)第1封信可以投入3个信箱中的任意一个,有3种投法;同理,第2,3,4封信各有3种投法.根据分步乘法计数原理,共有(种)投法.
故答案为:20;81.
9.(1)24;(2)18;(3)6.
【详解】(1)涂区有3种涂法,,,区域各有2种不同的涂法,
由分步乘法计数原理知将,,,四个区域涂色共有种不同的涂色方案;
(2)恰好用3种不同颜色涂四个区域,则,区域或,区域或,区域必同色,
由分类加法计数原理可得恰好用3种不同颜色涂四个区域共种不同涂色的方案;
(3)若恰好用2种不同颜色涂四个区域,则,区域必同色,且,区域必同色,
先从3种不同颜色中任取2种颜色,共3种不同的取法,然后用所取的2种颜色涂四个区域,共2种不同的涂法,
由分步乘法计数原理可得恰好用2种不同颜色涂完四个区域,共有种不同的涂色方案.
10.(1)360个,120个;(2)160个.
【详解】(1)偶数的个位数只能是2、4、6,有种排法,其他位上有种排法,
由分步乘法计数原理,知共有四位偶数=360(个);
能被5整除的数个位必须是5,故有=120(个)
(2)最高位上是7时大于6 500,有种,
最高位上是6时,百位上只能是7或5,故有2×种.
由分类加法计数原理知,这些四位数中大于6 500的共有+2×=160(个).
【高分突破】
1.B
【详解】本题可以把数归为“四位数”(含0006等),
因此比2 013小的“好数”为0×××,1×××,2 004,共三类数,
第一类可分为:00××,01××,…,0 600,共7类,共有7+6+…+2+1=28个数;
第二类可分为:10××,11××,…,1 500,共6类,共有6+5+4+3+2+1=21个数,
第二类可分为:2 004,共1个
故2 013为第28+21+1+1=51个数,故n=51.
故选:B.
2.D
【详解】涂色方案可分为两类,第一类只使用3种颜色的涂色方案,第二类使用4种颜色的涂色方案,只使用3种颜色的涂色方案有种,使用4种颜色的涂色方案种,所以不同的染色方案有种.故选D.
3.420
【详解】分四步进行分析:①区域涂色方案有5种;②区域涂色方案有4种;③区域涂色方案有3种;④对于区域,,若与颜色相同,则区域涂色方案有3种,若与颜色不同,则区域,涂色方案均有2种,所以区域,涂色方案共有(种).故不同的涂色方案有(种).
故答案为:420
4.20
【详解】依题意得,既会英语又会日语的有7+3-9=1(人),6人只会英语,2人只会日语.
第1类:从只会英语的6人中选一人有6种选法,此时选会日语的有2+1=3(种).
由分步乘法计数原理得N1=6×3=18(种);
第2类:从既会英语又会日语的人中选一人会英语的有1种选法,此时选会日语的有2种.
由分步乘法计数原理得N2=1×2=2(种).
综上,不同的选法共有N=N1+N2=18+2=20(种).
故答案为:20.
5.1886
【详解】设末尾为时的排列数为,用表示前3个数字分别为,,的排列数.
则,,
,,
,,
,,
,
所以总数为.
故答案为:1886.
6.(1)①种;②种;(2)种.
【详解】(1)①因为奇数号盒只放奇数号小球,每盒只放一个小球,所以先从3个奇数号小球中任取2个放入奇数号盒中,有种放法;再将剩余的4个小球中的2个放入余下的2个盒中,有种放法.从而不同的放法种数为.
②因为奇数号小球必须放在奇数号盒中,每盒只放一个小球,所以分两类讨论:
第一类,取1个奇数号小球和3个偶数号小球放入盒中,共有种放法;
第二类,取2个奇数号小球和2个偶数号小球放入盒中,共有种放法.
从而不同的放法种数为.
(2)由于不许空盒且将6个小球都放入盒中,所以考虑对6个小球先进行分组再放入盒中,分两类:
第一类,将6个小球分成1,1,2,2四组的不同分法种数为,再放入4个盒中,有种放法;
第二类,将6个小球分成1,1,1,3四组的不同分法种数为,再放入4个盒中,有种放法.
从而所有不同的放法种数为.
7.(1)种;(2)题图①:种,题图②:种;(3).
【详解】(1)由题意知题图①中的四个区域,每个区域有种涂色方案,共有种方案;
(2)题图①:第一步,涂,有种不同的涂法;
第二步,涂,与的颜色不相同,有种不同的涂法;
第三步,涂,与、的颜色都不相同,有种不同的涂法;
第四步,涂,只需与的颜色不相同,有种不同的涂法.
所以共有种不同的涂色方案.
题图②:第一步,涂,有种不同的涂法;
第二步,涂,与的颜色不相同,有种不同的涂法;
第三步,涂,与、的颜色都不相同,有种不同的涂法;
第四步,涂,与、的颜色都不相同,有种不同的涂法.
所以共有种不同的涂色方案;
(3)前三步与题图①的涂法类似,分别有、、种不同的涂法,
第四步,涂,与、的颜色都不相同,有种不同的涂法.
所以共有种不同的涂色方案,
所以,,所以.
8.(1)216;(2)216;(3)193.
【详解】(1)个位上的数字必须是0或5,个位上是0,有个;个位上是5,若不含0,则有个;若含0,但0不作首位,则0的位置有种排法,其余各位有种排法,故共有++=216(个)能被5整除的五位数.
(2)能被3整除的条件是各位数字之和能被3整徐,则5个数可能有{1,2,3,4,5}和{0,1,2,4,5}两种情况,能够组成的五位数分别有和个.
故能被3整除的五位数有(个).
(3)由于是六位数,首位数字不能为0,首位数字为1有个数,首位数字为2,万位上为0,1,3中的一个有个数,∴240 135的项数是++1=193,即240 135是数列的第193项
9.(1)20;(2)10.
【详解】(1)从A中取一个数作为十位数字,有4种不同的取法,从B中取一个数作为个位数字,有5种不同的取法.由分步乘法计数原理可知,能组成4×5=20(个)不同的两位数.
(2)要组成十位数字小于个位数字的两位数,可分如下情况:
当个位数字为9时,十位上的数字有4种取法,能组成4个十位数字小于个位数字的两位数;
当个位数字为7时,十位上的数字有3种取法,能组成3个十位数字小于个位数字的两位数;
当个位数字为5时,十位上的数字有2种取法,能组成2个十位数字小于个位数字的两位数;
当个位数字为3时,十位上的数字有1种取法,能组成1个十位数字小于个位数字的两位数.
所以组成的十位数字小于个位数字的两位数有1+2+3+4=10(个).
【考点梳理】
知识点一 两个计数原理的区别与联系
分类加法计数原理 分步乘法计数原理
相同点 回答的都是有关做一件事的不同方法种数的问题
不同点 针对的是“分类”问题
不同点 各种方法相互独立,用其中任何一种方法都可以做完这件事 各个步骤中的方法互相依存,只有每一个步骤都完成才算做完这件事
知识点二 两个计数原理的应用
用两个计数原理解决计数问题时,最重要的是在开始计算之前要仔细分析两点:
一、要完成的“一件事”是什么;二、需要分类还是需要分步.
(1)分类要做到“不重不漏”,分类后再分别对每一类进行计数,最后用分类加法计数原理求和,得到总数.
(2)分步要做到“步骤完整”,即完成了所有步骤,恰好完成任务.分类后再计算每一步的方法数,最后根据分步乘法计数原理,把完成每一步的方法数相乘,得到总数.
【题型归纳】
题型一、实际问题中的计数问题
1.甲与其四位同事各有一辆私家车,车牌尾数分别是9,0,2,1,5,为遵守当地某月5日至9日5天的限行规定(奇数日车牌尾数为奇数的车通行,偶数日车牌尾数为偶数的车通行),五人商议拼车出行,每天任选一辆符合规定的车,但甲的车最多只能用一天,则不同的用车方案种数为( )
A.64 B.80 C.96 D.120
2.在填写高考志愿表时,一名高中毕业生了解到,A,B两所大学各有一些自己感兴趣的强项专业,如表:
A大学 B大学
生物学 数学
化学 会计学
医学 信息技术学
二物理学 法学
工程学
如果这名同学只能选一个专业,那么他共有多少种选择?
3.计算机编程人员在编写好程序以后需要对程序进行测试.程序员需要知道到底有多少条执行路径(即程序从开始到结束的路线),以便知道需要提供多少个测试数据.一般地,一个程序模块由许多子模块组成.如图,这是一个具有许多执行路径的程序模块,它有多少条执行路径?另外,为了减少测试时间,程序员需要设法减少测试次数.你能帮助程序员设计一个测试方法,以减少测试次数吗?
题型二、代数中的计数问题
4.甲 乙两人做从装有14个玻璃球的盒子中抓取玻璃球的游戏,规定:甲 乙两人轮流抓取,每次至少抓取1个,最多抓取4个,最后一次取完者获胜.若甲先抓取,为确保甲一定获胜,则甲第一次应该抓取的玻璃球个数为( )
A.1 B.2 C.3 D.4
5.集合,满足,,若,中的元素个数分别不是,中的元素,则满足条件的集合的个数为____.(用数字作答)
6.从1,2,3,4,7,9六个数中,任取两个数作为对数的底数和真数,则所有不同的对数值的个数为____.
7.已知集合M∈{1,-2,3),N∈{-4,5,6,-7},从两个集合中各取一个元素作为点的坐标,则这样的坐标在直角坐标系中可表示第一、二象限内不同的点的个数是( )
A.18 B.10 C.16 D.14
题型三、几何计数问题
8.一个国际象棋棋盘(由8×8个方格组成),其中有一个小方格因破损而被剪去(破损位置不确定).“L”形骨牌由三个相邻的小方格组成,如图所示.现要将这个破损的棋盘剪成数个“L”形骨牌,则( )
A.至多能剪成19块“L”形骨牌
B.至多能剪成20块“L”形骨牌
C.最多能剪成21块“L”形骨牌
D.前三个答案都不对
9.以三棱柱的顶点为顶点共可组成________个不同的三棱锥?
10.在如图所示的的方格纸上(每个小方格均为正方形),共有________个矩形、________个正方形.
题型四、数字排列问题
11.用数字、、组成五位数,且数字、、至少都出现一次,这样的五位数共有( )个
A. B. C. D.
12.由数字0,1,2,3,4,5组成没有重复数字的六位数,其中个位数字小于十位数字的共有( )
A.210个 B.300个
C.464个 D.600个
13.从、、、这个数字中选出个不同的数字组成个三位数,试写出所有满足条件的三位数.
14.“回文数”是指从左到右读与从右到左读都一样的正整数.如22,121,343,94249等.显然,2位数的回文数有9个,即11,22,33,…,99;3位数的回文数有90个:101,111,121,…,191,202,…,999.求:
(1)4位数的回文数个数;
(2)位数的回文数个数.
题型五、涂色问题
15.将红、黄、绿三种不同的颜色均涂入图中五个区域中,每个区域涂一种颜色,且相邻的区域不能涂同一种颜色,不同的涂色方法共有__种.(三种颜色必须用全,以数字作答)
16.在中国地图上,西部五省(甘肃、四川、青海、新疆、西藏)如图所示,有四种颜色供选择,要求每省涂一色,相邻省不同色,则不同的涂色方法有( )种.
A.48 B.72 C.96 D.120
17.如图,在四棱锥中,现给5个顶点安装彩色灯泡,要求相邻顶点的位置不得使用同一颜色,有4种不同颜色可供选择,则不同的安装方法共有( )
A.48种 B.72种 C.80种 D.96种
题型六、其它计数问题
18.据《孙子算经》记载,算筹计数法则是:“凡算之法,先识其位,一纵十横,百立千僵,千十相望,万百相当."算筹计数法有纵 横两种形式,如图为纵式计数形式,一竖表示1个单位,一横表示5个单位,例如三竖一横表示8.
现从上图中选择三个数构成等比数列,则能构成等比数列的组合中所有数的纵式计数形式中共有横数为( )
A.1 B.2 C.3 D.4
19.位顾客将各自的帽子随意放在衣帽架上,然后,每人随意取走一顶帽子,则人拿的都不是自己的帽子方案总数为____________.(用数字作答)
20.将编号为,,,,,,的小球放入编号为,,,,,,的七个盒子中,每盒放一球,若有且只有三个盒子的编号与放入的小球的编号相同,则不同的放法种数为______________.
【双基达标】
1.菊花是开封市花,1983年开封市人大把菊花命名为开封市“市花”,并且举办“菊花花会”,每年10月18日至11月18日为“菊花花会”的会期.如图是某展区的一个菊花布局图,现有5个不同品种的菊花可供选择,要求相邻的两个展区不使用同一种菊花,则不同的布置方法有( )
A.种 B.种 C.种 D.种
2.埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,如图,将一个四棱锥的每一个顶点染上一种颜色,并使同一条棱上的两端异色,如果只有5种颜色可供使用,则不同的染色方法总数为( )
A. B. C. D.
3.为了支援山区教育,现在安排名大学生到个学校进行支教活动,每个学校至少安排人,其中甲校至少要安排名大学生,则不同的安排方法共有( )种
A. B. C. D.
4.从1,2,3,4,5,6,7,8,9这9个数字中任取两个,其中一个作为底数,另一个作为真数,则可以得到不同对数值的个数为( )
A.64 B.56 C.53 D.51
5.如果一个三位正整数如“”满足且,则称这个三位数为“凸数”(如120,343,275等),那么所有三位数中“凸数”的个数为______.
6.小明有4枚完全相同的硬币,每个硬币都分正反两面.他想把4个硬币摆成一摞,且满足相邻两枚硬币的正面与正面不相对,不同的摆法有________种.
7.某班一天上午有4节课,每节都需要安排一名教师去上课,现从,,,,,6名教师中安排4人分别上一节课,第一节课只能从,两人中安排一人,第四节课只能从,两人中安排一人,则不同的安排方案共有______种.(用数字作答)
8.(1)某外语组有9人,每人至少会英语和日语中的一门,其中7人会英语,3人会日语,从中选出会英语和日语的各一人,有______种不同的选法;
(2)将4封信投入3个信箱中,共有______种不同的投法.
9.如图所示的,,,按照下列要求涂色.
(1)用3种不同颜色填涂图中,,,四个区域,且使相邻区域不同色,若按从左到右依次涂色,有多少种不同的涂色方案?
(2)若恰好用3种不同颜色给,,,四个区域涂色,且相邻区域不同色,共有多少种不同的涂色方案?
(3)若有3种不同颜色,恰好用2种不同颜色涂完四个区域,且相邻区域不同色,共有多少种不同的涂色方案?
10.用1、2、3、4、5、6、7这7个数字组成没有重复数字的四位数.
(1)这些四位数中偶数有多少个 能被5整除的有多少个
(2)这些四位数中大于6 500的有多少个
【高分突破】
1.如果正整数a的各位数字之和等于6,那么称a为“好数”(如:6,24,2013等均为“好数”),将所有“好数”从小到大排成一列a1,a2,a3,…,若an=2 013,则n=( )
A.50 B.51 C.52 D.53
2.四色定理(Four color theorem)又称四色猜想,是世界近代三大数学难题之一.它是于1852年由毕业于伦敦大学的格斯里(Francis Guthrie)提出来的,其内容是“任何一张地图只用四种颜色就能使具有共同边界的国家着上不同的颜色.”四色问题的证明进程缓慢,直到1976年,美国数学家运用电子计算机证明了四色定理.现某校数学兴趣小组给一个底面边长互不相等的直四棱柱容器的侧面和下底面染色,提出如下的“四色问题”:要求相邻两个面不得使用同一种颜色,现有4种颜色可供选择,则不同的染色方案有( )
A.18种 B.36种 C.48种 D.72种
3.如图为我国数学家赵爽在为《周髀算经》作注时验证勾股定理的示意图,现提供5种颜色给其中5个小区域,,,,涂色,规定每个区域只涂1种颜色,相邻区域颜色不相同,则不同的涂色方案共有______种.
4.某外语组9人,每人至少会英语和日语中的一门,其中7人会英语,3人会日语,从中选出会英语和日语的各一人,则不同的选法有________种.
5.若某四位数满足,则称该四位数为“收敛四位数”,则所有“收敛四位数”的个数是______.(用数字作答)
6.有标号为1,2,3,4,5,6的6个小球和标号为1,2,3,4的4个盒.
(1)从6个小球中选出4个放入4个盒中,每盒只放1个小球.
①求奇数号盒只放奇数号小球的不同放法种数;
②求奇数号小球必须放在奇数号盒中的不同放法种数.
(2)若不许空盒且将6个小球都放入4个盒中,求所有不同的放法种数.
7.用种不同的颜色给如图所示的、、、四个区域涂色.
(1)若相邻区域能用同一种颜色,则图①有多少种不同的涂色方案?
(2)若相邻区域不能用同一种颜色,当时,图①、图②各有多少种不同的涂色方案?
(3)若相邻区域不能用同一种颜色,图③有种不同的涂色方案,求的值.
8.用0,1,2,3,4,5这六个数字可以组成多少个无重复数字的
(1)能被5整除的五位数;
(2)能被3整除的五位数;
(3)若所有的六位数按从小到大的顺序组成一个数列{an},则240 135是第几项.
9.已知集合A={2,4,6,8},B={1,3,5,7,9},从A中取一个数作为十位数字,从B中取一个数作为个位数字,问:
(1)能组成多少个不同的两位数?
(2)能组成多少个十位数字小于个位数字的两位数?
【答案详解】
【题型归纳】
1.B
【详解】5日至9日,日期尾数分别为5,6,7,8,9,有3天是奇数日,2天是偶数日.第一步,安排偶数日出行,每天都有2种选择,共有2×2=4(种);第二步,安排奇数日出行,分两类,第一类,选1天安排甲的车,另外2天安排其他车,有3×2×2=12(种),第二类,不安排甲的车,每天都有2种选择,共有=8(种),共有12+8=20(种).根据分步乘法计数原理,不同的用车方案种数为4×20=80.
故选:B.
2.9.
【详解】这名同学可以选择A,B两所大学中的一所.在A大学中有5种专业选择方法,在B大学中有4种专业选择方法,∵没有一个强项专业是两所大学共有的,∴根据分类加法计数原理,这名同学可能的专业选择种数.
3.7371.
【详解】由分类加法计数原理,子模块1、子模块2、子模块3中的子路径条数共为
;
子模块4、子模块5中的子路径条数共为,
又由分步乘法计数原理,整个模块的执行路径条数共为;
在实际测试中,程序员总是把每一个子模块看成一个黑箱,
即通过只考察是否执行了正确的子模块的方式来测试整个模块,
这样,他可以先分别单独测试5个模块,以考察每个子模块的工作是否正常,
总共需要的测试次数为,
再测试各个模块之间的信息交流是否正常,
只需要测试程序第1步中的各个子模块和第2步中的各个子模块之间的信息交流是否正常,
需要的测试次数为,
如果每个子模块都工作正常,并且各个子模块之间的信息交流也正常,那么整个程序模块就工作正常,
这样,测试整个模块的次数就变为,
显然,178与7371的差距是非常大的,故用以上测试方法,可以减少测试次数.
4.D
【详解】因为每人每次至少抓取1个,最多抓取4个
当两人所拿的和为5时,有
所以甲第一次应该抓取4个玻璃球,后面只要满足甲拿的球与乙拿的球和为5,则甲一定获胜
故选:D
5.44.
【详解】含1元,含7元,则,,于是,,共;同理:含2元,含6元,共6个;含3元,含5元,共15个;含5元,含3元,共15个;含6元,含2元,共6个;含7元,含1元,共1个.
6.17
【详解】
①当取得两个数中有一个是1时,则1只能作真数,此时loga1=0,a=2或3或4或7或9.
②所取的两个数不含有1时,即从2,3,4,7,9中任取两个,分别作为底数与真数可有=20个对数,但是其中,
.
综上可知:共可以得到20+1﹣4=17个不同的对数值.
故答案为17.
点睛:本题是一道易错题,防止重复,其中,
,处理计数原理问题,贵在不重不漏,需要同学们熟练掌握对数的运算法则.
7.D
【详解】M中的元素作点的横坐标,N中的元素作点的纵坐标,
在第一象限的点共有2×2个,在第二象限的点共有1×2个.
N中的元素作点的横坐标,M中的元素作点的纵坐标,
在第一象限的点共有2×2个,在第二象限的点共有2×2个.
所求不同的点的个数是2×2+1×2+2×2+2×2=14(个).
故选:D.
8.C
【详解】考虑2×3的6块方格,如图:,每一块这样的骨牌含有2块“L”形骨牌
一共可以剪成10块这样的骨牌,和一个田字格,田字格可以剪1块“L”形骨牌,则一共21块“L”形骨牌.
只要将破损的方格所在位置剪成一个恰当的田字格即可,所以一定能够剪成21块“L”形骨牌.
如图所示
故选:C
9.12
【详解】从个顶点中选出个的方法数有种,其中共面的有种(即个侧面),故可以构成不同三棱锥的方法数有种.
44. 280 60
10.【详解】根据题意,7×4的方格纸上,有5条水平方向的线,8条竖直方向的线,
在5条水平方向的线中任选2条,在8条竖直方向的线中任选2条,就可以组成一个矩形,
则可以组成个矩形;
设方格纸上的小方格的边长为1,
当正方形的边长为1时,有7×4=28个正方形,
当正方形的边长为2时,有6×3=18个正方形,
当正方形的边长为3时,有5×2=10个正方形,
当正方形的边长为4时,有4×1=4个正方形,
则有28+18+10+4=60个正方形;
故答案为:280,60.
11.B
【详解】首先考虑全部的情况,即每个数位均有种选择,共有个,
其中包含数字全部相同只有种情况,
还有只含有个数字的共有个,
因此,满足条件的五位数的个数为个.
故选:B.
12.B
【详解】由题意得,个位数字小于十位数字,
所以个位数字只能是0,1,2,3,4共5种类型,
每种类型分别有个,
共有
故选:B
13.【详解】所有满足条件的三位数分别为:、、、、、、、、、、、、、、、、、,共个.
14.(1)90
(2)
【详解】(1)由题设,四位数回文:
∴共有90个.
(2)位数,则中间的数字有10种选法,而两侧的数字只需排好一侧,则另一侧确定,
不妨排前n位数字,显然第一位数字有9种选法,其余都有10种选法,
∴共有个回文数.
15.42
【详解】由题意,不妨从左至右按编号,由于三种颜色必须用全,第一步涂一号有三种涂法,第二步涂二号有二种涂法第三步涂三号时可分为两类研究,若三号与一号同则后两框必一框涂色与一号二号不同,与若三号与一号不同,由于三种颜色已全部用上,故后两框涂色只需要满足同色不相邻即可,
故总的涂色方法为种
故答案为:42.
16.B
【详解】先进行编号:新疆、甘肃、青海、西藏、四川,
按的顺序进行涂色,其中颜色可以相同或不相同,
所以不同的涂色方法数有种.
故选:B
17.B
【详解】若A,C使用同一颜色,则由分步计数原理可知有(种);
若A,C不使用同一颜色,则由分步计数原理可知有(种),
由分类计数原理可得共有(种),
故选:B.
18.D
【详解】正整数1~9中能构成等比数列的三个数一共有四组,分别是1,2,4;2,4,8;1,3,9;4,6,9.
其中只有6,8,9的纵式计数形式中各有1横,所以共有4横
故选:D
19.
【详解】记位顾客分别为甲、乙、丙、丁.
假设甲拿了乙的帽子,则乙拿了甲的帽子,丙拿了丁的帽子,丁拿了丙的帽子;或乙拿丙的帽子,丙拿了丁的帽子,丁拿了甲的帽子;或乙拿了丁的帽子,丙拿了甲的帽子,丁拿了丙的帽子.
若甲拿了丙或丁的帽子,同理可知,符合条件的方案数均为种.
综上所述,人拿的都不是自己的帽子方案总数为.
故答案为:.
20.
【详解】按两步进行计算:
1. 选出盒子的编号与小球编号相同的3个编号,共有种选法;
2.对余下的4个编号的球,将它们放置到不同盒子中,且盒子的编号与球的编号不同,有种方法,
故不同的放法种数为,
故答案为:
【双基达标】
1.D
【详解】先布置中心区域共有种方法,从开始沿逆时针方向进行布置四周的区域,则有种布置方法,有种布置方法.
如果与选用同一种菊花,则有种布置方法;如果与选用不同种类菊花,则有种布置方法,有种布置方法.按照分步乘法与分类加法计数原理,
则全部的布置方法有(种),
故选:.
2.C
【详解】分两步,先将四棱锥一侧面三顶点染色,然后再分类考虑另外两顶点的染色数,用乘法原理可求解,由题设,四棱锥S - ABCD的顶点S, A, B所染的颜色互不相同,它们共有种染色方法;
当染好时,不妨设所染颜色依次为1, 2, 3,若C染2,则D可染3或4或5,有3种染法;若C染4,则D可染3或5,有2种染法;若C染5,则D可染3或4,有2种染法,即当S, A, B染好时,C, D还有7种染法.
故不同的染色方法有种.
故选:C
3.C
【详解】若甲校分名大学生,此时有种分配方法;
若甲校分名大学生,此时有种分配方法.
综上所述,共有种分配方法.
故选:C.
4.C
【详解】由于1只能作为真数,则以1为真数,从其余各数中任取一数为底数,对数值均为0,
从除1外的其余各数中任取两数分别作为对数的底数和真数,共能组成个对数式,
其中,,,,,重复了4次,
所以得到不同对数值的个数为.
故选:C
5.240
【详解】若,则“凸数”为120与121,共有(个);
若,则“凸数”有(个);
若,则“凸数”有(个);
若,则“凸数”有(个);
若,则“凸数”有(个);
若,则“凸数”有(个);
若,则“凸数”有(个);
若,则“凸数”有(个).
所以所有三位数中“凸数”的个数为.
故答案为:240.
6.5
【详解】
记反面为1,正面为2,则正反依次相对有12121212,21212121两种;有两枚反面相对有21121212,21211212,21212112三种,共5种摆法.
故答案为:5.
7.36
【详解】不同的安排方案有两类办法:
第一类,第一节课若安排,则第四节课只能安排,第二节课从剩余4人中任选1人,第三节课从剩余3人中任选1人,共有种排法;
第二类,第一节课若安排,则第四节课可安排或,第二节课从剩余4人中任选1人,第三节课从剩余3人中任选1人,共有种排法,
因此不同的安排方案有种.
故答案为:36
8. 20 81
【详解】(1)共分三类:第一类,当选出的会英语的人既会英语又会日语时,选会日语的人有2种选法;
第二类,当选出的会日语的人既会英语又会日语时,选会英语的人有6种选法;
第三类,当既会英语又会日语的人不参与选择时,则需从只会日语和只会英语的人中各选一人,有(种)选法.
故共有(种)选法.
(2)第1封信可以投入3个信箱中的任意一个,有3种投法;同理,第2,3,4封信各有3种投法.根据分步乘法计数原理,共有(种)投法.
故答案为:20;81.
9.(1)24;(2)18;(3)6.
【详解】(1)涂区有3种涂法,,,区域各有2种不同的涂法,
由分步乘法计数原理知将,,,四个区域涂色共有种不同的涂色方案;
(2)恰好用3种不同颜色涂四个区域,则,区域或,区域或,区域必同色,
由分类加法计数原理可得恰好用3种不同颜色涂四个区域共种不同涂色的方案;
(3)若恰好用2种不同颜色涂四个区域,则,区域必同色,且,区域必同色,
先从3种不同颜色中任取2种颜色,共3种不同的取法,然后用所取的2种颜色涂四个区域,共2种不同的涂法,
由分步乘法计数原理可得恰好用2种不同颜色涂完四个区域,共有种不同的涂色方案.
10.(1)360个,120个;(2)160个.
【详解】(1)偶数的个位数只能是2、4、6,有种排法,其他位上有种排法,
由分步乘法计数原理,知共有四位偶数=360(个);
能被5整除的数个位必须是5,故有=120(个)
(2)最高位上是7时大于6 500,有种,
最高位上是6时,百位上只能是7或5,故有2×种.
由分类加法计数原理知,这些四位数中大于6 500的共有+2×=160(个).
【高分突破】
1.B
【详解】本题可以把数归为“四位数”(含0006等),
因此比2 013小的“好数”为0×××,1×××,2 004,共三类数,
第一类可分为:00××,01××,…,0 600,共7类,共有7+6+…+2+1=28个数;
第二类可分为:10××,11××,…,1 500,共6类,共有6+5+4+3+2+1=21个数,
第二类可分为:2 004,共1个
故2 013为第28+21+1+1=51个数,故n=51.
故选:B.
2.D
【详解】涂色方案可分为两类,第一类只使用3种颜色的涂色方案,第二类使用4种颜色的涂色方案,只使用3种颜色的涂色方案有种,使用4种颜色的涂色方案种,所以不同的染色方案有种.故选D.
3.420
【详解】分四步进行分析:①区域涂色方案有5种;②区域涂色方案有4种;③区域涂色方案有3种;④对于区域,,若与颜色相同,则区域涂色方案有3种,若与颜色不同,则区域,涂色方案均有2种,所以区域,涂色方案共有(种).故不同的涂色方案有(种).
故答案为:420
4.20
【详解】依题意得,既会英语又会日语的有7+3-9=1(人),6人只会英语,2人只会日语.
第1类:从只会英语的6人中选一人有6种选法,此时选会日语的有2+1=3(种).
由分步乘法计数原理得N1=6×3=18(种);
第2类:从既会英语又会日语的人中选一人会英语的有1种选法,此时选会日语的有2种.
由分步乘法计数原理得N2=1×2=2(种).
综上,不同的选法共有N=N1+N2=18+2=20(种).
故答案为:20.
5.1886
【详解】设末尾为时的排列数为,用表示前3个数字分别为,,的排列数.
则,,
,,
,,
,,
,
所以总数为.
故答案为:1886.
6.(1)①种;②种;(2)种.
【详解】(1)①因为奇数号盒只放奇数号小球,每盒只放一个小球,所以先从3个奇数号小球中任取2个放入奇数号盒中,有种放法;再将剩余的4个小球中的2个放入余下的2个盒中,有种放法.从而不同的放法种数为.
②因为奇数号小球必须放在奇数号盒中,每盒只放一个小球,所以分两类讨论:
第一类,取1个奇数号小球和3个偶数号小球放入盒中,共有种放法;
第二类,取2个奇数号小球和2个偶数号小球放入盒中,共有种放法.
从而不同的放法种数为.
(2)由于不许空盒且将6个小球都放入盒中,所以考虑对6个小球先进行分组再放入盒中,分两类:
第一类,将6个小球分成1,1,2,2四组的不同分法种数为,再放入4个盒中,有种放法;
第二类,将6个小球分成1,1,1,3四组的不同分法种数为,再放入4个盒中,有种放法.
从而所有不同的放法种数为.
7.(1)种;(2)题图①:种,题图②:种;(3).
【详解】(1)由题意知题图①中的四个区域,每个区域有种涂色方案,共有种方案;
(2)题图①:第一步,涂,有种不同的涂法;
第二步,涂,与的颜色不相同,有种不同的涂法;
第三步,涂,与、的颜色都不相同,有种不同的涂法;
第四步,涂,只需与的颜色不相同,有种不同的涂法.
所以共有种不同的涂色方案.
题图②:第一步,涂,有种不同的涂法;
第二步,涂,与的颜色不相同,有种不同的涂法;
第三步,涂,与、的颜色都不相同,有种不同的涂法;
第四步,涂,与、的颜色都不相同,有种不同的涂法.
所以共有种不同的涂色方案;
(3)前三步与题图①的涂法类似,分别有、、种不同的涂法,
第四步,涂,与、的颜色都不相同,有种不同的涂法.
所以共有种不同的涂色方案,
所以,,所以.
8.(1)216;(2)216;(3)193.
【详解】(1)个位上的数字必须是0或5,个位上是0,有个;个位上是5,若不含0,则有个;若含0,但0不作首位,则0的位置有种排法,其余各位有种排法,故共有++=216(个)能被5整除的五位数.
(2)能被3整除的条件是各位数字之和能被3整徐,则5个数可能有{1,2,3,4,5}和{0,1,2,4,5}两种情况,能够组成的五位数分别有和个.
故能被3整除的五位数有(个).
(3)由于是六位数,首位数字不能为0,首位数字为1有个数,首位数字为2,万位上为0,1,3中的一个有个数,∴240 135的项数是++1=193,即240 135是数列的第193项
9.(1)20;(2)10.
【详解】(1)从A中取一个数作为十位数字,有4种不同的取法,从B中取一个数作为个位数字,有5种不同的取法.由分步乘法计数原理可知,能组成4×5=20(个)不同的两位数.
(2)要组成十位数字小于个位数字的两位数,可分如下情况:
当个位数字为9时,十位上的数字有4种取法,能组成4个十位数字小于个位数字的两位数;
当个位数字为7时,十位上的数字有3种取法,能组成3个十位数字小于个位数字的两位数;
当个位数字为5时,十位上的数字有2种取法,能组成2个十位数字小于个位数字的两位数;
当个位数字为3时,十位上的数字有1种取法,能组成1个十位数字小于个位数字的两位数.
所以组成的十位数字小于个位数字的两位数有1+2+3+4=10(个).
