人教A版2019选择性必修第三册7.4.1 二项分布 学案(Word版含答案)
文档属性
| 名称 | 人教A版2019选择性必修第三册7.4.1 二项分布 学案(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 810.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-29 16:09:37 | ||
图片预览




文档简介
7.4 二项分布与超几何分布
7.4.1 二项分布
【知识梳理】
知识点一 n重伯努利试验及其特征
1.n重伯努利试验的概念
将一个伯努利试验独立地重复进行n次所组成的随机试验称为n重伯努利试验.
2.n重伯努利试验的共同特征
(1)同一个伯努利试验重复做n次.
(2)各次试验的结果相互独立.
知识点二 二项分布
一般地,在n重伯努利试验中,设每次试验中事件A发生的概率为p(0称随机变量X服从二项分布,记作X~B(n,p).
知识点三 二项分布的均值与方差
若X~B(n,p),则E(X)=np,D(X)=np(1-p).
【题型归纳】
n重伯努利试验的判断
1.独立重复试验满足的条件是___________.(填序号)
①每次试验之间是相互独立的;
②每次试验只有发生和不发生两种情况;
③每次试验中发生的机会是均等的;
④每次试验发生的事件是互斥的.
2.判断下列试验是不是重伯努利试验.
(1)依次投掷四枚质地不同的硬币,次正面向上;
(2)某人射击,击中目标的概率是稳定的,他连续射击了次,其中次击中;
(3)口袋中装有个白球,个红球,个黑球,依次从中抽取个球,恰好抽出个白球.
n重伯努利试验的概率
3.一只不透明的口袋中有形状、大小完全相同的10个球,其中有两个球的编号为1,三个球的编号为2,三个球编号为3,两个球编号为4.
(1)甲有放回地从袋子中取3次,每次取一个球,求恰有两次取到2号球的概率;
(2)甲从袋子口一次取出三个球,以表示取出的三个球中的最小号码,写出的分布列及数学期望.
4.已知某种节能灯的使用寿命至少为的概率为0.9,求在20只此种节能灯中,
(1)有18只使用寿命至少为的概率;
(2)至少有15只使用寿命至少为的概率;
(3)至少有2只达不到使用寿命至少为的概率.
三、二项分布的应用
5.甲 乙二人进行定点投篮比赛,已知甲 乙二人每次投进的概率均为,两人各投1次称为一轮投篮.
(1)求乙在前3次投篮中,恰好投进2个球的概率;
(2)设前3轮投篮中,甲与乙进球个数差的绝对值为随机变量,求的分布列与期望.
6.接种新冠疫苗,可以有效降低感染新冠肺炎的几率,某地区有A,B,C三种新冠疫苗可供居民接种,假设在某个时间段该地区集中接种第一针疫苗,而且这三种疫苗的供应都很充足,为了节省时间和维持良好的接种秩序,接种点设置了号码机,号码机可以随机地产生A,B,C三种号码(产生每个号码的可能性都相等),前去接种第一针疫苗的居民先从号码机上取一张号码,然后去接种与号码相对应的疫苗(例如:取到号码A,就接种A种疫苗,以此类推).若甲,乙,丙,丁四个人各自独立的去接种第一针新冠疫苗.
(1)求这四个人中恰有一个人接种A种疫苗的概率;
(2)记甲,乙,丙,丁四个人中接种A种疫苗的人数为X,求随机变量X的分布列和数学期望.
【双基达标】
1.将一枚均匀的骰子先后抛掷3次,至少出现两次点数为3的概率为( )
A. B. C. D.
2.已知随机变量X服从二项分布X~B(4,),( )
A. B. C. D.
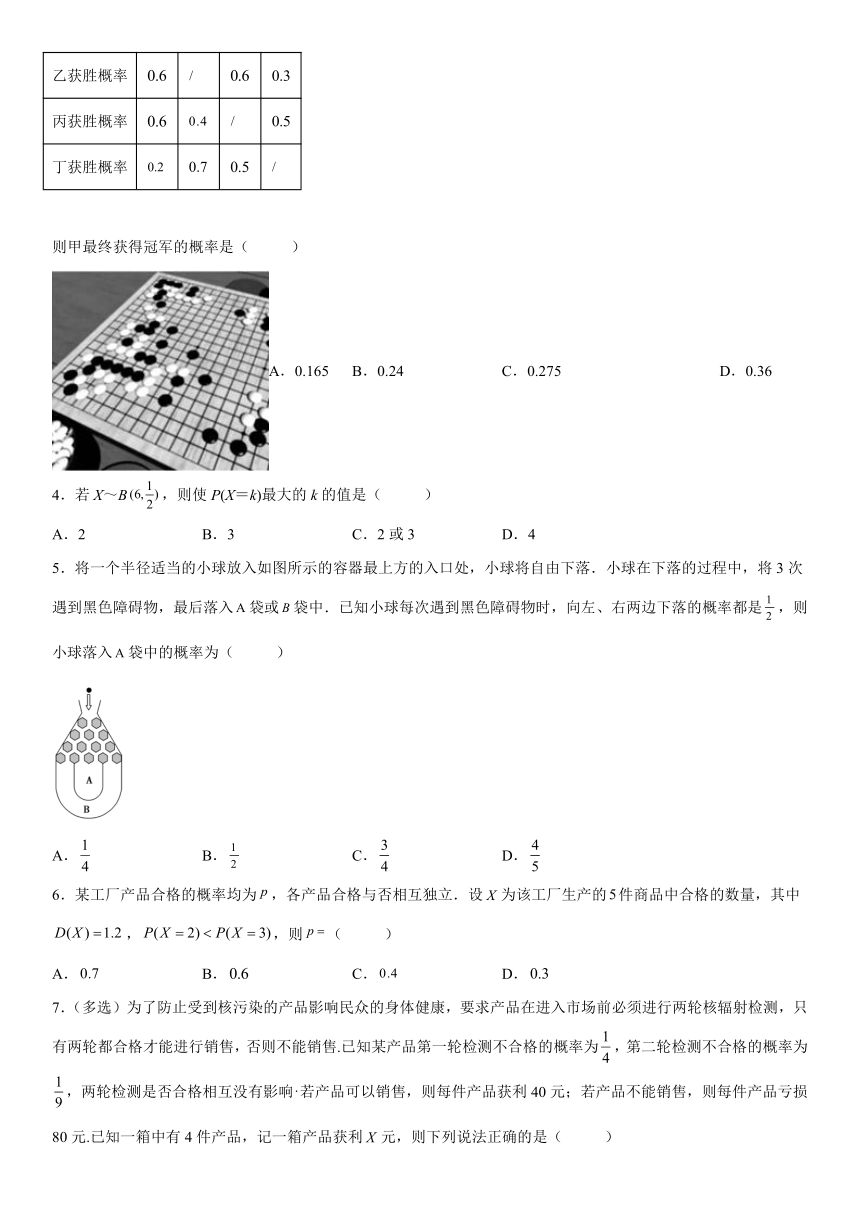
3.围棋起源于中国,据先秦典籍世本记载:“尧造围棋,丹朱善之”,至今已有四千多年历史.围棋不仅能抒发意境、陶冶情操、修身养性、生慧增智,而且还与天象易理、兵法策略、治国安邦等相关联,蕴含着中华文化的丰富内涵.在某次国际围棋比赛中,规定甲与乙对阵,丙与丁对阵,两场比赛的胜者争夺冠军,根据以往战绩,他们之间相互获胜的概率如下:
甲 乙 丙 丁
甲获胜概率
乙获胜概率
丙获胜概率
丁获胜概率
则甲最终获得冠军的概率是( )
A.0.165 B.0.24 C.0.275 D.0.36
4.若X~B,则使P(X=k)最大的k的值是( )
A.2 B.3 C.2或3 D.4
5.将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落的过程中,将3次遇到黑色障碍物,最后落入袋或袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是,则小球落入袋中的概率为( )
A. B. C. D.
6.某工厂产品合格的概率均为,各产品合格与否相互独立.设为该工厂生产的件商品中合格的数量,其中,,则( )
A. B. C. D.
7.(多选)为了防止受到核污染的产品影响民众的身体健康,要求产品在进入市场前必须进行两轮核辐射检测,只有两轮都合格才能进行销售,否则不能销售.已知某产品第一轮检测不合格的概率为,第二轮检测不合格的概率为,两轮检测是否合格相互没有影响若产品可以销售,则每件产品获利40元;若产品不能销售,则每件产品亏损80元.已知一箱中有4件产品,记一箱产品获利元,则下列说法正确的是( )
A.该产品能销售的概率为
B.若表示一箱产品中可以销售的件数,则
C.若表示一箱产品中可以销售的件数,则
D.
8.(多选)下列事件不是n重伯努利试验的是( )
A.运动员甲射击一次,“射中9环”与“射中8环”
B.甲、乙两运动员各射击一次,“甲射中10环”与“乙射中9环”
C.甲、乙两运动员各射击一次,“甲、乙都射中目标”与“甲、乙都没射中目标”
D.在相同的条件下,甲射击10次,5次击中目标
9.某人参加一次考试,共有4道试题,至少答对其中3道试题才能合格.若他答每道题的正确率均为0.5,并且答每道题之间相互独立,则他能合格的概率为______.
10.中国光谷(武汉)某科技公司生产一批同型号的光纤通讯仪器,每台仪器的某一部件由三个电子元件按如图方式连接而成,若元件1或元件2正常工作,且元件3正常工作,则该部件正常工作.由大数据统计显示:三个电子元件的使用寿命(单位:小时)均服从正态分布(1000,).且各个元件能否正常工作相互独立.现从这批仪器中随机抽取1000台检测该部件的工作情况(各部件能否正常工作相互独立),那么这1000台仪器中该部件的使用寿命超过1000小时的平均值为______台.
11.一个箱子中装有4个红球和3个白球,那么
(1)一次取出2个球,在已知它们颜色相同的情况下,求该颜色是红色的慨率;
(2)一次取出1个球,取出后记录颜色并放回箱中,取球3次,求取到红球个数X的期望与方差.
12.某煤矿发生透水事故,作业区有若干人员被困.救援队从入口进入之后,有,两条巷道通往作业区(如图),巷道有,,三个易堵塞点,两点被堵塞的概率都是,巷道有,两个易堵塞点,两点被堵塞的概率分别为,.
(1)求巷道中,三个易堵塞点最多有一个被堵塞的概率;
(2)若巷道中堵塞点的个数为,求的分布列及均值;
(3)请你按照“平均堵塞点少的巷道是较好的抢险路线”的标准,帮助救援队选择一条抢险路线,并说明理由.
【高分突破】
1.为了防止受到核污染的产品影响我国民众的身体健康,有关部门要求产品在进入市场前必须进行两轮核辐射检测,只有两轮都合格才能进行销售,否则不能销售.已知某产品第一轮检测不合格的概率为,第二轮检测不合格的概率为,两轮检测是否合格相互没有影响,若产品可以销售,则每件产品获利40元;若产品不能销售,则每件产品亏损80元.已知一箱中有4件产品,记一箱产品获利X元,则( )
A. B. C. D.
2.某综艺节目中,有一个盲拧魔方游戏,就是玩家先观察魔方状态并进行记忆,记住后蒙住眼睛快速还原魔方.为了解某市盲拧魔方爱好者的水平状况,某兴趣小组在全市范围内随机抽取了100名盲拧魔方爱好者进行调查,得到的情况如表所示:
用时/秒 [5,10] (10,15] (15,20] (10,15]
男性人数 15 22 14 9
女性人数 5 11 17 7
以这100名盲拧魔方爱好者用时不超过10秒的频率,代替全市所有盲拧魔方爱好者用时不超过10秒的概率,每位盲拧魔方爱好者用时是否超过10秒相互独立.若该兴趣小组在全市范围内再随机抽取20名盲拧魔方爱好者进行测试,其中用时不超过10秒的人数最有可能(即概率最大)是( )A.2 B.3 C.4 D.5
3.设随机变量,满足:,,若,则( )
A.3 B. C.4 D.
4.设随机变量,记.在研究的最大值时,某数学兴趣小组的同学发现:若为正整数,则时,,此时这两项概率均为最大值;若为非整数,当取的整数部分,则是唯一的最大值.以此为理论基础,有同学重复投掷一枚质地均匀的股子并实时记录点数1出现的次数.当投郑到第30次时,记录到此时点数1出现7次,若继续再进行70次投掷试验,则当投掷到第100次时,点数1总共出现的次数为( )的概率最大
A.16 B.17 C.18 D.19
5.(多选)一口袋中有大小和质地相同的4个红球和2个白球,则下列结论正确的是( )
A.从中任取3球,恰有一个白球的概率是
B.从中有放回的取球6次,每次任取一球,恰好有两个白球的概率为
C.从中不放回的取球2次,每次任取1球,若第一次已取到了红球,则第二次再次取到红球的概率为
D.从中有放回的取球3次,每次任取一球,则至少有一次取到红球的概率为
6.(多选)为了防止受到核污染的产品影响民众的身体健康,要求产品在进入市场前必须进行两轮核辐射检测,只有两轮都合格才能进行销售,否则不能销售已知某产品第一轮检测不合格的概率为,第二轮检测不合格的概率为,两轮检测是否合格相互没有影响若产品可以销售,则每件产品获利40元;若产品不能销售,则每件产品亏损80元.已知一箱中有4件产品,记一箱产品获利X元,则下列说法正确的是( )
A.该产品能销售的概率为 B.若表示一箱产品中可以销售的件数,则
C.若表示一箱产品中可以销售的件数,则; D.
7.甲、乙两名运动员进行羽毛球比赛,已知每局比赛甲胜的概率为,乙胜的概率为,且各局比赛结果相互独立.当比赛采取局胜制时,甲用4局赢得比赛的概率为.现甲,乙进行局比赛,设甲胜的局数为则________________.
8.在一次以“二项分布的性质”为主题的数学探究活动中,立德中学高三某小组的学生表现优异,发现的正确结论得到老师和同学的一致好评.设随机变量,记,.在研究的最大值时,小组同学发现:若为正整数,则时,,此时这两项概率均为最大值;若为非整数,当取的整数部分,则是唯一的最大值.以此为理论基础,有同学重复投掷一枚质地均匀的骰子并实时记录点数1出现的次数.当投掷到第20次时,记录到此时点数1出现5次,若继续再进行80次投掷试验,则当投掷到第100次时,点数1总共出现的次数为____________的概率最大.
9.某通讯商场推出一款新手机,分为甲、乙、丙、丁4种不同的配置型号.该商场对近期售出的100部该款手机的情况进行了统计,绘制如下表格:
配置 甲 乙 丙 丁
频数 25 40 15 20
(1)每售出一部甲、乙、丙、丁配置型号的手机可分别获得利润600元、400元、500元、450元,根据以上100名消费者的购机情况,求该商场销售一部该款手机的平均利润;
(2)该商场某天共销售了4部该款手机,每销售一部该款手机的型号相互独立,其中甲配置型号手机售出的数量为,将样本频率视为概率,求的概率分布列及期望.
10.某厂生产两种产品,对两种产品的某项指标进行检测,现各抽取100件产品作为样本,其指标值的频率分布直方图如图所示:以该项指标作为衡量产品质量的标准,该项指标划分等级和收益率如下表,其中.
(注:收益率)
等级 一等品 二等品 三等品
指标值
产品收益率
(1)求的值;
(2)将频率分布直方图中的频率近似看作概率,用样本估计总体.
①从产品中随机抽取3件,求其中一等品件数的分布列及数学期望;
②在总投资额相同的情况下,若全部投资产品或产品,试分析投资哪种产品收益更大.
【答案详解】
【题型归纳】
1.①②③
【详解】在相同的条件下,重复地做次试验,各次试验的结果相互独立,每次试验只有发生和不发生两种情况,每次试验中发生的机会是均等的,那么一般就称它们为次独立重复试验,所以①②③正确,④不正确,
故答案为:①②③.
2.(1)不是;(2)是;(3)不是.
【详解】(1)由于试验的条件不同(质地不同),因此不是重伯努利试验;
(2)某人射击且击中的概率是稳定的,因此是重伯努利试验;
(3)每次抽取,试验的结果有三种不同的颜色,且每种颜色出现的可能性不相等,因此不是重伯努利试验.
3.(1)
(2)分布列见解析,
【详解】(1)由题意,每次取一个球,取到编号为2的概率为,
所以恰有两次取到2号球的概率为
(2)由题意可得,
则;
;
;
所以的分布列如下:
所以
4.【详解】(1)根据题意,有18只使用寿命至少为的概率.
(2)至少有15只使用寿命至少为的概率.
(3)至少有2只达不到使用寿命至少为的概率.
5.(1)
(2)分布列答案见解析,数学期望:
【详解】(1)设“乙在前3次投篮中,恰好投进2个球”为事件,
则.
答:乙在前3次投篮中,恰好投进2个球的概率为.
(2)的所有可能取值为0,1,2,3.
设前3轮投篮中,甲进球个数为,乙进球个数为,
则,的取值均为0,1,2,3,
,
,
,
.
所以,
,
,
.
所以的分布列为
0 1 2 3
数学期望为.
6.(1);(2)分布列见解析;期望为.
【详解】(1)记四个人中恰有一个人接种A疫苗的事件为M,
则,
所以四个人中恰有一个人接种A疫苗的概率为.
(2)由题意可知,的取值依次为0,1,2,3,4.
且,
故随机变量的分布列为
0 1 2 3 4
.
【双基达标】
1.D
【详解】将一枚均匀的筛子先后抛掷3次,每次出现点数为3的概率都是
至少出现两次点数为3的概率为:
故选:D
2.D
【详解】∵随机变量X服从二项分布X~B(4,),
∴.
故选:D.
3.B
【详解】甲最终获得冠军的概率,
故选:B.
4.B
【详解】,
则,得,
所以当时,,当时,,
从而时,取得最大值.
故选:B.
5.C
【详解】由于小球每次遇到黑色障碍物时,有一次向左和两次向右或两次向左和一次向右下落时,小球将落入A袋,所以.
故选:C.
6.B
【详解】由已知X服从与参数为5,p的二项分布,
∴ ,,,
又,,
∴ ,,
∴ ,
故选:B.
7.ABD
【详解】选项A. 该产品能销售的概率为,故选项A正确.
选项B. 由A 可得每件产品能销售的概率为
一箱中有4件产品,记一箱产品获利元,则,故选项B正确.
选项C. 由题意,不选项C不正确.
选项D. 由题意,即4件产品中有2件能销售,有2件产品不能销售.
所以,故选项D正确.
故选:ABD
8.ABC
【详解】AC符合互斥事件的概念,是互斥事件,不是独立重复试验;
B是相互独立事件,但是“甲射中10环”与“乙射中9环” 的概率不一定相同,因此不是独立重复试验;
D中在相同的条件下,甲射击10次,是独立重复试验
故选:ABC
9.
【详解】某人参加考试,4道题目中,答对的题目数满足二项分布,
所以
故答案为:
10.375
【详解】由正态分布可知,每个元件正常工作超过10000小时的概率为,
则部件正常工作超过10000小时的概率为,
又1000台仪器的该部件工作服从二项分布,所以平均值为台.
故答案为:375.
11.(1) (2)
【详解】(1)在已知它们颜色相同的情况下,该颜色是红色的慨率为
(2)由题意可知,一次取出1个球,取得红球的概率为
取出后记录颜色并放回箱中,取球3次,则X的可能取值为0,1,2,3,且X~B(3,),
所以E(X)=np=3×=,
D(X)=np(1﹣p)=3×.
12.(1);(2)分布列见解析,均值为;(3)选择巷道为抢险路线较好,理由见解析.
【详解】(1)设“巷道中,三个易堵塞点最多有一个被堵塞”为事件,
则.
(2)依题意,知的所有可能取值为0,1,2.
,,
.所以随机变量的分布列为
0 1 2
.
(3)设巷道中堵塞点的个数为,则,所以.
因为,所以选择巷道为抢险路线较好.
【高分突破】
1.B
【详解】由题意得该产品能销售的概率为,
易知X的所有可能取值为﹣320,﹣200,﹣80,40,160,
设表示一箱产品中可以销售的件数,则,
所以,
所以,,
,
故,
,
故选:B.
2.C
【详解】根据题意得,1名盲拧魔方爱好者用时不超过10秒的概率为,设随机抽取的20名盲拧魔方爱好者中用时不超过10秒的人数为,
则,其中,,
当时,由,
得,化简得,
解得,又,所以,所以这20名盲拧魔方爱好者中用时不超过10秒的人数最有可能是4.
故选:C.
3.C
【详解】由于随机变量满足: ,,
,
解得:,即
,
又随机变量,满足:,
,
故选:C.
4.C
【详解】由题意出现1点次数,由已知理论得次时(表示的整数部分),概率最大,又前30次中出现了7次,
所以当投掷到第100次时,点数1总共出现的次数为时概率最大.
故选:C.
5.ABD
【详解】对选项A,从中任取3球,恰有一个白球的概率是,故A正确;
对选项B,从中有放回的取球6次,每次任取一球,
则取到白球的个数,
故恰好有两个白球的概率为;
对选项C,从中不放回的取球2次,每次任取1球,记A为“第一次取到红球”,
B为“第二次取到红球”,则所求概率为,故C错误。
对选项D,从中有放回的取球3次,每次任取一球,则取到红球的个数,
至少有一次取到红球的概率为,故D正确。
故选:ABD
6.ABD
【详解】选项A. 该产品能销售的概率为,故选项A正确;
选项B. 由A 可得每件产品能销售的概率为
一箱中有4件产品,记一箱产品获利元,则,故选项B正确;
选项C. 由题意,故选项C不正确;
选项D. 由题意,即4件产品中有2件能销售,有2件产品不能销售,
所以,故选项D正确.
故选:ABD.
7..
【详解】由题意知: ,所以,
所以每局比赛甲胜的概率为,乙胜的概率为,
由题意知:随机变量,
所以.
故答案为:.
8.18
【详解】继续再进行80次投掷试验,出现点数为1次数服从二项分布,
由,结合题中结论可知,时概率最大,即后面80次中出现13次点数1的概率最大,
加上前面20次中的5次,所以出现18次的概率最大.
故答案为:18.
9.(1)475
(2)分布列见解析,
【详解】(1)依题意,,
所以该商场销售一部手机的平均利润为475元.
(2)该商场每销售一部手机,该手机为甲配置型号手机的概率为,
由题意,甲配置型号手机售出的数量为服从二项分布,即,
则所有可能取值为,
,
故的分布列为:
由二项分布的期望公式:.
10.(1);
(2)①分布列见解析,;②投资产品的收益更大.
【详解】(1)由题可得,解得.
(2)①由直方图知:产品为一等品的概率是,二等品概率是,三等品概率是,
由题知随机抽取3件是一等品的件数X可能的取值是0,1,2,3,且,,,
,,
则的分布列为:
0 1 2 3
∴.
②由题可得,产品为一等品的概率为,二等品的概率为,三等品的概率为,
产品为一等品的概率为,二等品的概率为,三等品的概率为,
产品的收益:,
产品的收益:,
∴,
因为,
所以,即,
故投资产品的收益更大.
7.4.1 二项分布
【知识梳理】
知识点一 n重伯努利试验及其特征
1.n重伯努利试验的概念
将一个伯努利试验独立地重复进行n次所组成的随机试验称为n重伯努利试验.
2.n重伯努利试验的共同特征
(1)同一个伯努利试验重复做n次.
(2)各次试验的结果相互独立.
知识点二 二项分布
一般地,在n重伯努利试验中,设每次试验中事件A发生的概率为p(0
知识点三 二项分布的均值与方差
若X~B(n,p),则E(X)=np,D(X)=np(1-p).
【题型归纳】
n重伯努利试验的判断
1.独立重复试验满足的条件是___________.(填序号)
①每次试验之间是相互独立的;
②每次试验只有发生和不发生两种情况;
③每次试验中发生的机会是均等的;
④每次试验发生的事件是互斥的.
2.判断下列试验是不是重伯努利试验.
(1)依次投掷四枚质地不同的硬币,次正面向上;
(2)某人射击,击中目标的概率是稳定的,他连续射击了次,其中次击中;
(3)口袋中装有个白球,个红球,个黑球,依次从中抽取个球,恰好抽出个白球.
n重伯努利试验的概率
3.一只不透明的口袋中有形状、大小完全相同的10个球,其中有两个球的编号为1,三个球的编号为2,三个球编号为3,两个球编号为4.
(1)甲有放回地从袋子中取3次,每次取一个球,求恰有两次取到2号球的概率;
(2)甲从袋子口一次取出三个球,以表示取出的三个球中的最小号码,写出的分布列及数学期望.
4.已知某种节能灯的使用寿命至少为的概率为0.9,求在20只此种节能灯中,
(1)有18只使用寿命至少为的概率;
(2)至少有15只使用寿命至少为的概率;
(3)至少有2只达不到使用寿命至少为的概率.
三、二项分布的应用
5.甲 乙二人进行定点投篮比赛,已知甲 乙二人每次投进的概率均为,两人各投1次称为一轮投篮.
(1)求乙在前3次投篮中,恰好投进2个球的概率;
(2)设前3轮投篮中,甲与乙进球个数差的绝对值为随机变量,求的分布列与期望.
6.接种新冠疫苗,可以有效降低感染新冠肺炎的几率,某地区有A,B,C三种新冠疫苗可供居民接种,假设在某个时间段该地区集中接种第一针疫苗,而且这三种疫苗的供应都很充足,为了节省时间和维持良好的接种秩序,接种点设置了号码机,号码机可以随机地产生A,B,C三种号码(产生每个号码的可能性都相等),前去接种第一针疫苗的居民先从号码机上取一张号码,然后去接种与号码相对应的疫苗(例如:取到号码A,就接种A种疫苗,以此类推).若甲,乙,丙,丁四个人各自独立的去接种第一针新冠疫苗.
(1)求这四个人中恰有一个人接种A种疫苗的概率;
(2)记甲,乙,丙,丁四个人中接种A种疫苗的人数为X,求随机变量X的分布列和数学期望.
【双基达标】
1.将一枚均匀的骰子先后抛掷3次,至少出现两次点数为3的概率为( )
A. B. C. D.
2.已知随机变量X服从二项分布X~B(4,),( )
A. B. C. D.
3.围棋起源于中国,据先秦典籍世本记载:“尧造围棋,丹朱善之”,至今已有四千多年历史.围棋不仅能抒发意境、陶冶情操、修身养性、生慧增智,而且还与天象易理、兵法策略、治国安邦等相关联,蕴含着中华文化的丰富内涵.在某次国际围棋比赛中,规定甲与乙对阵,丙与丁对阵,两场比赛的胜者争夺冠军,根据以往战绩,他们之间相互获胜的概率如下:
甲 乙 丙 丁
甲获胜概率
乙获胜概率
丙获胜概率
丁获胜概率
则甲最终获得冠军的概率是( )
A.0.165 B.0.24 C.0.275 D.0.36
4.若X~B,则使P(X=k)最大的k的值是( )
A.2 B.3 C.2或3 D.4
5.将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落的过程中,将3次遇到黑色障碍物,最后落入袋或袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是,则小球落入袋中的概率为( )
A. B. C. D.
6.某工厂产品合格的概率均为,各产品合格与否相互独立.设为该工厂生产的件商品中合格的数量,其中,,则( )
A. B. C. D.
7.(多选)为了防止受到核污染的产品影响民众的身体健康,要求产品在进入市场前必须进行两轮核辐射检测,只有两轮都合格才能进行销售,否则不能销售.已知某产品第一轮检测不合格的概率为,第二轮检测不合格的概率为,两轮检测是否合格相互没有影响若产品可以销售,则每件产品获利40元;若产品不能销售,则每件产品亏损80元.已知一箱中有4件产品,记一箱产品获利元,则下列说法正确的是( )
A.该产品能销售的概率为
B.若表示一箱产品中可以销售的件数,则
C.若表示一箱产品中可以销售的件数,则
D.
8.(多选)下列事件不是n重伯努利试验的是( )
A.运动员甲射击一次,“射中9环”与“射中8环”
B.甲、乙两运动员各射击一次,“甲射中10环”与“乙射中9环”
C.甲、乙两运动员各射击一次,“甲、乙都射中目标”与“甲、乙都没射中目标”
D.在相同的条件下,甲射击10次,5次击中目标
9.某人参加一次考试,共有4道试题,至少答对其中3道试题才能合格.若他答每道题的正确率均为0.5,并且答每道题之间相互独立,则他能合格的概率为______.
10.中国光谷(武汉)某科技公司生产一批同型号的光纤通讯仪器,每台仪器的某一部件由三个电子元件按如图方式连接而成,若元件1或元件2正常工作,且元件3正常工作,则该部件正常工作.由大数据统计显示:三个电子元件的使用寿命(单位:小时)均服从正态分布(1000,).且各个元件能否正常工作相互独立.现从这批仪器中随机抽取1000台检测该部件的工作情况(各部件能否正常工作相互独立),那么这1000台仪器中该部件的使用寿命超过1000小时的平均值为______台.
11.一个箱子中装有4个红球和3个白球,那么
(1)一次取出2个球,在已知它们颜色相同的情况下,求该颜色是红色的慨率;
(2)一次取出1个球,取出后记录颜色并放回箱中,取球3次,求取到红球个数X的期望与方差.
12.某煤矿发生透水事故,作业区有若干人员被困.救援队从入口进入之后,有,两条巷道通往作业区(如图),巷道有,,三个易堵塞点,两点被堵塞的概率都是,巷道有,两个易堵塞点,两点被堵塞的概率分别为,.
(1)求巷道中,三个易堵塞点最多有一个被堵塞的概率;
(2)若巷道中堵塞点的个数为,求的分布列及均值;
(3)请你按照“平均堵塞点少的巷道是较好的抢险路线”的标准,帮助救援队选择一条抢险路线,并说明理由.
【高分突破】
1.为了防止受到核污染的产品影响我国民众的身体健康,有关部门要求产品在进入市场前必须进行两轮核辐射检测,只有两轮都合格才能进行销售,否则不能销售.已知某产品第一轮检测不合格的概率为,第二轮检测不合格的概率为,两轮检测是否合格相互没有影响,若产品可以销售,则每件产品获利40元;若产品不能销售,则每件产品亏损80元.已知一箱中有4件产品,记一箱产品获利X元,则( )
A. B. C. D.
2.某综艺节目中,有一个盲拧魔方游戏,就是玩家先观察魔方状态并进行记忆,记住后蒙住眼睛快速还原魔方.为了解某市盲拧魔方爱好者的水平状况,某兴趣小组在全市范围内随机抽取了100名盲拧魔方爱好者进行调查,得到的情况如表所示:
用时/秒 [5,10] (10,15] (15,20] (10,15]
男性人数 15 22 14 9
女性人数 5 11 17 7
以这100名盲拧魔方爱好者用时不超过10秒的频率,代替全市所有盲拧魔方爱好者用时不超过10秒的概率,每位盲拧魔方爱好者用时是否超过10秒相互独立.若该兴趣小组在全市范围内再随机抽取20名盲拧魔方爱好者进行测试,其中用时不超过10秒的人数最有可能(即概率最大)是( )A.2 B.3 C.4 D.5
3.设随机变量,满足:,,若,则( )
A.3 B. C.4 D.
4.设随机变量,记.在研究的最大值时,某数学兴趣小组的同学发现:若为正整数,则时,,此时这两项概率均为最大值;若为非整数,当取的整数部分,则是唯一的最大值.以此为理论基础,有同学重复投掷一枚质地均匀的股子并实时记录点数1出现的次数.当投郑到第30次时,记录到此时点数1出现7次,若继续再进行70次投掷试验,则当投掷到第100次时,点数1总共出现的次数为( )的概率最大
A.16 B.17 C.18 D.19
5.(多选)一口袋中有大小和质地相同的4个红球和2个白球,则下列结论正确的是( )
A.从中任取3球,恰有一个白球的概率是
B.从中有放回的取球6次,每次任取一球,恰好有两个白球的概率为
C.从中不放回的取球2次,每次任取1球,若第一次已取到了红球,则第二次再次取到红球的概率为
D.从中有放回的取球3次,每次任取一球,则至少有一次取到红球的概率为
6.(多选)为了防止受到核污染的产品影响民众的身体健康,要求产品在进入市场前必须进行两轮核辐射检测,只有两轮都合格才能进行销售,否则不能销售已知某产品第一轮检测不合格的概率为,第二轮检测不合格的概率为,两轮检测是否合格相互没有影响若产品可以销售,则每件产品获利40元;若产品不能销售,则每件产品亏损80元.已知一箱中有4件产品,记一箱产品获利X元,则下列说法正确的是( )
A.该产品能销售的概率为 B.若表示一箱产品中可以销售的件数,则
C.若表示一箱产品中可以销售的件数,则; D.
7.甲、乙两名运动员进行羽毛球比赛,已知每局比赛甲胜的概率为,乙胜的概率为,且各局比赛结果相互独立.当比赛采取局胜制时,甲用4局赢得比赛的概率为.现甲,乙进行局比赛,设甲胜的局数为则________________.
8.在一次以“二项分布的性质”为主题的数学探究活动中,立德中学高三某小组的学生表现优异,发现的正确结论得到老师和同学的一致好评.设随机变量,记,.在研究的最大值时,小组同学发现:若为正整数,则时,,此时这两项概率均为最大值;若为非整数,当取的整数部分,则是唯一的最大值.以此为理论基础,有同学重复投掷一枚质地均匀的骰子并实时记录点数1出现的次数.当投掷到第20次时,记录到此时点数1出现5次,若继续再进行80次投掷试验,则当投掷到第100次时,点数1总共出现的次数为____________的概率最大.
9.某通讯商场推出一款新手机,分为甲、乙、丙、丁4种不同的配置型号.该商场对近期售出的100部该款手机的情况进行了统计,绘制如下表格:
配置 甲 乙 丙 丁
频数 25 40 15 20
(1)每售出一部甲、乙、丙、丁配置型号的手机可分别获得利润600元、400元、500元、450元,根据以上100名消费者的购机情况,求该商场销售一部该款手机的平均利润;
(2)该商场某天共销售了4部该款手机,每销售一部该款手机的型号相互独立,其中甲配置型号手机售出的数量为,将样本频率视为概率,求的概率分布列及期望.
10.某厂生产两种产品,对两种产品的某项指标进行检测,现各抽取100件产品作为样本,其指标值的频率分布直方图如图所示:以该项指标作为衡量产品质量的标准,该项指标划分等级和收益率如下表,其中.
(注:收益率)
等级 一等品 二等品 三等品
指标值
产品收益率
(1)求的值;
(2)将频率分布直方图中的频率近似看作概率,用样本估计总体.
①从产品中随机抽取3件,求其中一等品件数的分布列及数学期望;
②在总投资额相同的情况下,若全部投资产品或产品,试分析投资哪种产品收益更大.
【答案详解】
【题型归纳】
1.①②③
【详解】在相同的条件下,重复地做次试验,各次试验的结果相互独立,每次试验只有发生和不发生两种情况,每次试验中发生的机会是均等的,那么一般就称它们为次独立重复试验,所以①②③正确,④不正确,
故答案为:①②③.
2.(1)不是;(2)是;(3)不是.
【详解】(1)由于试验的条件不同(质地不同),因此不是重伯努利试验;
(2)某人射击且击中的概率是稳定的,因此是重伯努利试验;
(3)每次抽取,试验的结果有三种不同的颜色,且每种颜色出现的可能性不相等,因此不是重伯努利试验.
3.(1)
(2)分布列见解析,
【详解】(1)由题意,每次取一个球,取到编号为2的概率为,
所以恰有两次取到2号球的概率为
(2)由题意可得,
则;
;
;
所以的分布列如下:
所以
4.【详解】(1)根据题意,有18只使用寿命至少为的概率.
(2)至少有15只使用寿命至少为的概率.
(3)至少有2只达不到使用寿命至少为的概率.
5.(1)
(2)分布列答案见解析,数学期望:
【详解】(1)设“乙在前3次投篮中,恰好投进2个球”为事件,
则.
答:乙在前3次投篮中,恰好投进2个球的概率为.
(2)的所有可能取值为0,1,2,3.
设前3轮投篮中,甲进球个数为,乙进球个数为,
则,的取值均为0,1,2,3,
,
,
,
.
所以,
,
,
.
所以的分布列为
0 1 2 3
数学期望为.
6.(1);(2)分布列见解析;期望为.
【详解】(1)记四个人中恰有一个人接种A疫苗的事件为M,
则,
所以四个人中恰有一个人接种A疫苗的概率为.
(2)由题意可知,的取值依次为0,1,2,3,4.
且,
故随机变量的分布列为
0 1 2 3 4
.
【双基达标】
1.D
【详解】将一枚均匀的筛子先后抛掷3次,每次出现点数为3的概率都是
至少出现两次点数为3的概率为:
故选:D
2.D
【详解】∵随机变量X服从二项分布X~B(4,),
∴.
故选:D.
3.B
【详解】甲最终获得冠军的概率,
故选:B.
4.B
【详解】,
则,得,
所以当时,,当时,,
从而时,取得最大值.
故选:B.
5.C
【详解】由于小球每次遇到黑色障碍物时,有一次向左和两次向右或两次向左和一次向右下落时,小球将落入A袋,所以.
故选:C.
6.B
【详解】由已知X服从与参数为5,p的二项分布,
∴ ,,,
又,,
∴ ,,
∴ ,
故选:B.
7.ABD
【详解】选项A. 该产品能销售的概率为,故选项A正确.
选项B. 由A 可得每件产品能销售的概率为
一箱中有4件产品,记一箱产品获利元,则,故选项B正确.
选项C. 由题意,不选项C不正确.
选项D. 由题意,即4件产品中有2件能销售,有2件产品不能销售.
所以,故选项D正确.
故选:ABD
8.ABC
【详解】AC符合互斥事件的概念,是互斥事件,不是独立重复试验;
B是相互独立事件,但是“甲射中10环”与“乙射中9环” 的概率不一定相同,因此不是独立重复试验;
D中在相同的条件下,甲射击10次,是独立重复试验
故选:ABC
9.
【详解】某人参加考试,4道题目中,答对的题目数满足二项分布,
所以
故答案为:
10.375
【详解】由正态分布可知,每个元件正常工作超过10000小时的概率为,
则部件正常工作超过10000小时的概率为,
又1000台仪器的该部件工作服从二项分布,所以平均值为台.
故答案为:375.
11.(1) (2)
【详解】(1)在已知它们颜色相同的情况下,该颜色是红色的慨率为
(2)由题意可知,一次取出1个球,取得红球的概率为
取出后记录颜色并放回箱中,取球3次,则X的可能取值为0,1,2,3,且X~B(3,),
所以E(X)=np=3×=,
D(X)=np(1﹣p)=3×.
12.(1);(2)分布列见解析,均值为;(3)选择巷道为抢险路线较好,理由见解析.
【详解】(1)设“巷道中,三个易堵塞点最多有一个被堵塞”为事件,
则.
(2)依题意,知的所有可能取值为0,1,2.
,,
.所以随机变量的分布列为
0 1 2
.
(3)设巷道中堵塞点的个数为,则,所以.
因为,所以选择巷道为抢险路线较好.
【高分突破】
1.B
【详解】由题意得该产品能销售的概率为,
易知X的所有可能取值为﹣320,﹣200,﹣80,40,160,
设表示一箱产品中可以销售的件数,则,
所以,
所以,,
,
故,
,
故选:B.
2.C
【详解】根据题意得,1名盲拧魔方爱好者用时不超过10秒的概率为,设随机抽取的20名盲拧魔方爱好者中用时不超过10秒的人数为,
则,其中,,
当时,由,
得,化简得,
解得,又,所以,所以这20名盲拧魔方爱好者中用时不超过10秒的人数最有可能是4.
故选:C.
3.C
【详解】由于随机变量满足: ,,
,
解得:,即
,
又随机变量,满足:,
,
故选:C.
4.C
【详解】由题意出现1点次数,由已知理论得次时(表示的整数部分),概率最大,又前30次中出现了7次,
所以当投掷到第100次时,点数1总共出现的次数为时概率最大.
故选:C.
5.ABD
【详解】对选项A,从中任取3球,恰有一个白球的概率是,故A正确;
对选项B,从中有放回的取球6次,每次任取一球,
则取到白球的个数,
故恰好有两个白球的概率为;
对选项C,从中不放回的取球2次,每次任取1球,记A为“第一次取到红球”,
B为“第二次取到红球”,则所求概率为,故C错误。
对选项D,从中有放回的取球3次,每次任取一球,则取到红球的个数,
至少有一次取到红球的概率为,故D正确。
故选:ABD
6.ABD
【详解】选项A. 该产品能销售的概率为,故选项A正确;
选项B. 由A 可得每件产品能销售的概率为
一箱中有4件产品,记一箱产品获利元,则,故选项B正确;
选项C. 由题意,故选项C不正确;
选项D. 由题意,即4件产品中有2件能销售,有2件产品不能销售,
所以,故选项D正确.
故选:ABD.
7..
【详解】由题意知: ,所以,
所以每局比赛甲胜的概率为,乙胜的概率为,
由题意知:随机变量,
所以.
故答案为:.
8.18
【详解】继续再进行80次投掷试验,出现点数为1次数服从二项分布,
由,结合题中结论可知,时概率最大,即后面80次中出现13次点数1的概率最大,
加上前面20次中的5次,所以出现18次的概率最大.
故答案为:18.
9.(1)475
(2)分布列见解析,
【详解】(1)依题意,,
所以该商场销售一部手机的平均利润为475元.
(2)该商场每销售一部手机,该手机为甲配置型号手机的概率为,
由题意,甲配置型号手机售出的数量为服从二项分布,即,
则所有可能取值为,
,
故的分布列为:
由二项分布的期望公式:.
10.(1);
(2)①分布列见解析,;②投资产品的收益更大.
【详解】(1)由题可得,解得.
(2)①由直方图知:产品为一等品的概率是,二等品概率是,三等品概率是,
由题知随机抽取3件是一等品的件数X可能的取值是0,1,2,3,且,,,
,,
则的分布列为:
0 1 2 3
∴.
②由题可得,产品为一等品的概率为,二等品的概率为,三等品的概率为,
产品为一等品的概率为,二等品的概率为,三等品的概率为,
产品的收益:,
产品的收益:,
∴,
因为,
所以,即,
故投资产品的收益更大.
