两角和与差的三角函数[下学期]
文档属性
| 名称 | 两角和与差的三角函数[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 446.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-04-02 00:00:00 | ||
图片预览










文档简介
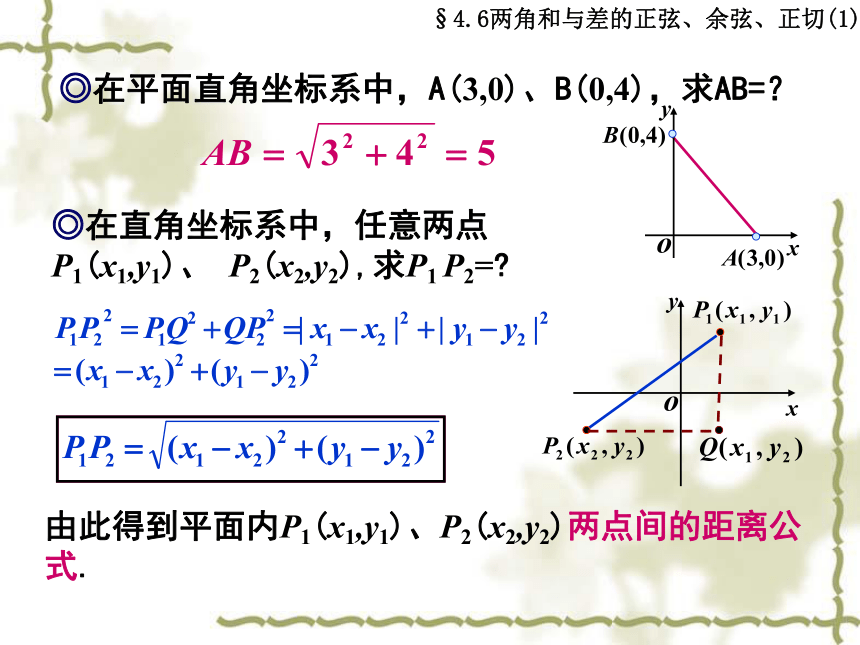
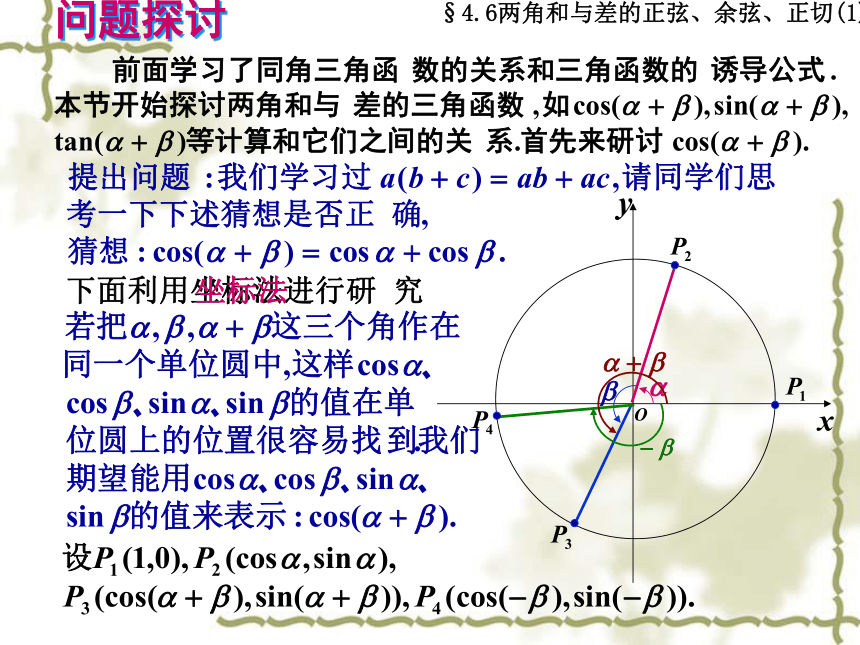
课件48张PPT。 两角和与差的三角函数沈阳市同泽高级中学数学组 郭玉敏§4.6 两角和与差的正弦、余弦、正切第一课时学习本节的目的要求: (1)了解并记住平面内两点间距离公式,理解平面内两点间距离公式的由来. (2)了解两角和的余弦公式的推导;能正确运用两角和的余弦公式进行简单三角函数式的化简、求值和恒等式变形. (3)培养利用旧知识推导、论证新知识的能力;积极主动的培养进行数学交流,获得数学知识的能力;自觉培养勇于探索的科学精神. 重点:余弦的和角公式. 难点:余弦的和角公式的推导.§4.6两角和与差的正弦、余弦、正切(1)阅读教材P34—35并回答下列问题:§4.6两角和与差的正弦、余弦、正切(1)阅读教材P34—35并回答下列问题:◎x轴上两点A(x1,0)、B(x2,0)之间的距离?◎y轴上两点C(0,y1)、D(0,y2)之间的距离?◎如果直线l平行x轴,A,B是l上的两点,A(x1,n)、 B(x2,n),求AB=?◎如果直线l1平行y轴,C,D是l1上的两点,C(m,y1)、D(n,y2),求CD=?◎在平面直角坐标系中,A(3,0)、B(0,4),求AB=?◎在直角坐标系中,任意两点P1(x1,y1)、 P2(x2,y2),求P1 P2=?由此得到平面内P1(x1,y1)、P2(x2,y2)两点间的距离公式.§4.6两角和与差的正弦、余弦、正切(1)§4.6两角和与差的正弦、余弦、正切(1)§4.6两角和与差的正弦、余弦、正切(1)问题探讨§4.6两角和与差的正弦、余弦、正切(1)公式强化训练题§4.6两角和与差的正弦、余弦、正切(1)§4.6两角和与差的正弦、余弦、正切(1)小 结§4.6 两角和与差的正弦、余弦、正切第二课时学习本节的目的要求: (1) 能由两角和的余弦公式推导出两角差的余弦公式. (2) 能正确运用两角和(差)的余弦公式进行简单三角函数式的化简、求值和恒等式变形. (3)培养利用旧知识推导、论证新知识的能力;积极主动的培养进行数学交流,获得数学知识的能力;通过公式的推导,培养逻辑思维能力,渗透符号与变元的数学思想. 重点:余弦的和(差)角公式的应用. 难点:“活用”公式(正用、逆用、变用).§4.6两角和与差的正弦、余弦、正切(2)复习与回固§4.6两角和与差的正弦、余弦、正切(2)§4.6两角和与差的正弦、余弦、正切(2)§4.6两角和与差的正弦、余弦、正切(2)§4.6两角和与差的正弦、余弦、正切(2)能力训练题§4.6两角和与差的正弦、余弦、正切(2)能力训练题§4.6两角和与差的正弦、余弦、正切(2)能力训练题§4.6两角和与差的正弦、余弦、正切(2)小 结§4.6 两角和与差的正弦、余弦、正切第三课时学习本节的目的要求: (1)了解两角和与差正弦公式、正切公式推导. (2)了解公式推导过程中的变换思想和整体思想方法,进一步熟悉化切为弦,化弦为切来解答有关三角函数问题的转化思想方法. (3)掌握两角和与差的正弦公式、正切公式,并会运用它们进行有关计算、化简、证明. 重点:两角和与差正弦公式、正切公式的应用. 难点:公式的综合应用.§4.6两角和与差的正弦、余弦、正切(3)复习与回固§4.6两角和与差的正弦、余弦、正切(3)问题探讨公式强化训练§4.6两角和与差的正弦、余弦、正切(3)§4.6两角和与差的正弦、余弦、正切(3)能力训练题§4.6两角和与差的正弦、余弦、正切(3)§4.6两角和与差的正弦、余弦、正切(3)问题探讨 §4.6两角和与差的正弦、余弦、正切(3)问题探讨(这里有什么要求?)(又有什么要求?)§4.6两角和与差的正弦、余弦、正切(3)问题探讨§4.6两角和与差的正弦、余弦、正切(3)能力训练题基础训练题小 结§4.6两角和与差的正弦、余弦、正切(3)两角和与差的正弦、余弦、正切公式的内在联系: 三角函数恒等变形实质是对角、函数名称的变化,而转化的依据就是一系列三角公式,如: ①同角三角函数关系——可实现函数名称的转化; ②诱导公式及和、差角的三角函数——可实现角的形式的转化.在应用公式时要注意它的逆向变换、多向变换,即对公式要“三会”:正用、逆用、变用.要注意通过拆角、拼角的技巧用已知角表示未知角.§4.6 两角和与差的正弦、余弦、正切综合应用(共三课时)学习本节的目的要求: (1)了解两角和与差正弦、余弦、正切公式之间的内在联系.培养逻辑推理能力. (2)掌握两角和与差的正弦公式、正切公式,并会运用它们进行有关计算、化简、证明. (3)通过实例熟悉一些解题的技巧并增强利用公式解决具体问题的灵活性. 重点:熟练、灵活的应用三角公式. 难点:变换中的技巧.两角和与差的正弦、余弦、正切公式的内在联系: 三角函数恒等变形实质是对角、函数名称的变化,而转化的依据就是一系列三角公式,如: ①同角三角函数关系——可实现函数名称的转化; ②诱导公式及和、差角的三角函数——可实现角的形式的转化.在应用公式时要注意它的逆向变换、多向变换,即对公式要“三会”:正用、逆用、变用.要注意通过拆角、拼角的技巧用已知角表示未知角.§4.6两角和与差的正弦、余弦、正切(4)复习与巩固§4.6两角和与差的正弦、余弦、正切(4)复习与巩固关于和角与差三角公式特别注意公式的结构,用活公式.§4.6两角和与差的正弦、余弦、正切(4)复习与巩固§4.6两角和与差的正弦、余弦、正切(4)复习与巩固§4.6两角和与差的正弦、余弦、正切(4)复习与巩固综合训练题§4.6两角和与差的正弦、余弦、正切(4)综合训练题§4.6两角和与差的正弦、余弦、正切(4)综合训练题§4.6两角和与差的正弦、余弦、正切(4)§4.6两角和与差的正弦、余弦、正切(4)综合训练题§4.6两角和与差的正弦、余弦、正切(4)综合训练题§4.6两角和与差的正弦、余弦、正切(4)综合训练题§4.6两角和与差的正弦、余弦、正切(4)综合训练题§4.6两角和与差的正弦、余弦、正切(4)综合训练题
