第六章 数据的收集与整理 【挑战满分】2022-2023学年数学七上阶段性复习精选精练(北师大版 含解析)
文档属性
| 名称 | 第六章 数据的收集与整理 【挑战满分】2022-2023学年数学七上阶段性复习精选精练(北师大版 含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 448.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-29 00:00:00 | ||
图片预览




文档简介
第六章数据的收集与整理
一、单选题
1.某次考试中,某班级的数学成绩被绘制成了如图所示的频数分布直方图.下列说法错误的是( )
A.得分在70~80分之间的人数最多
B.及格(不低于60分)的人数为26
C.得分在90~100分之间的人数占总人数的5%
D.该班的总人数为40
2.为了解某市七年级15000名学生的体重情况,从中抽取了500名学生进行测量,这500名学生的体重是( )
A.总体 B.个体 C.总体的一个样本 D.样本容量
3.在频数分布表中,所有频数之和( )
A.是1 B.等于所有数据的个数
C.与所有数据的个数无关 D.小于所有数据的个数
4.荆州古城是闻名遐迩的历史文化名城,“五一”期间相关部门对到荆州观光游客的出行方式进行了随机抽样调查,整理后绘制了两幅统计图(尚不完整).根据图中信息,下列结论错误的是( )
A.本次抽样调查的样本容量是5000
B.扇形图中的m为10%
C.样本中选择公共交通出行的有2500人
D.若“五一”期间到荆州观光的游客有50万人,则选择自驾方式出行的有25万人
5.某班组织了针对全班同学关于“你最喜欢的一项体育活动”的问卷调查后,绘制出频数分布直方图,由图可知,下列结论正确的是( )
最喜欢篮球的人数最多
B.最喜欢羽毛球的人数是最喜欢乒乓球人数的两倍
C.全班共有50名学生
D.最喜欢田径的人数占总人数的10 %
6.下列调查中,最适合采用全面调查(普查)的是( )
A.对我市中学生每周课外阅读时间情况的调查
B.对我市市民知晓“礼让行人”交通新规情况的调查
C.对我市中学生观看电影《厉害了,我的国》情况的调查
D.对我国首艘国产航母002型各零部件质量情况的调查
7.某频数分布直方图中,共有A,B,C,D,E五个小组,频数分别为10,15,25,35,10,则直方图中,长方形高的比为( )
A.2∶3∶5∶7∶2 B.1∶3∶4∶5∶1 C.2∶3∶5∶6∶2 D.2∶4∶5∶4∶2
8.“共享单车”为人们提供了一种经济便捷、绿色低碳的共享服务,成为城市交通出行的新方式,小文对他所在小区居民当月使用“共享单车”的次数进行了抽样调查,并绘制成了如图所示的频数分布直方图(每一组含前一个边界值,不含后一个边界值),则下列说法正确的是( )
A.小文一共抽样调查了20人
B.样本中当月使用“共享单车”次的人数最多
C.样本中当月使用“共享单车”不足30次的人数有14人
D.样本中当月使用次数不足30次的人数多于次的人数
9.已知一组数据8,6,10,10,13,11,8,10,12,12,9,8,7,12,9,11,9,10,11,10.那么频率是0.2的一组数据的范围是( )
A. B. C. D.
10.为了解我县参加2021年中考的4300名学生的体重情况,随机抽查了其中500名学生的体重进行统计分析,下列叙述正确的是( )
A.4300名学生是总体 B.每名学生是总体的一个个体
C.500名学生的体重情况是总体的一个样本 D.以上调查是普查
二、填空题
11.下表是某报纸公布的我国“九五”期间国内生产总值(GDP)的统计表,那么这几年间我国国内生产总值平均每年比上一年增长___万亿元.
年份 1996 1997 1998 1999 2000
GDP/万亿元 6.6 7.3 7.9 8.2 8.9
12.一个容量为的样本最大值是,最小值是,用频数分布直方图描述这一组数据,取组距为,则可以分成________组.
13.“阳光体育”运动在我市轰轰烈烈开展,为了解同学们最爱好的阳光体育运动项目,小王对本班50名同学进行了跳绳、羽毛球、篮球、乒乓球、踢毽子等运动项目最喜爱人数的调查,并根据调查结果绘制了如图所示的条形统计图,若将其转化为扇形统计图,那么最喜爱乒乓球的人数所在扇形区域的圆心角的度数为________.
14.以下调查:①了解全班同学每周体育锻炼的时间;②调查某批次汽车的抗撞击能力;③调查新闻联播的收视率.其中,适合全面调查的是__(填序号即可).
15.某同学要统计本校图书馆最受学生欢迎的图书种类,以下是打乱顺序的统计步骤:
①从扇形图中分析出最受学生欢迎的种类;
②去图书馆收集学生借阅图书的记录;
③绘制扇形图来表示各个种类所占的百分比;
④整理借阅图书记录并绘制频数分布表,正确统计步骤的顺序是_____.
16.为迎接学校艺术节,七年级某班进行班级歌词征集活动,作品上交时间为星期一至星期五.班委会把同学们上交作品件数按每天一组分组统计,绘制了频数分布直方图如下.已知从左至右各长方形的高的比为2:3:4:6:1,第二组的频数为9,则全班上交的作品有____件.
17.永州市教育部门为了了解全市中小学安全教育情况,对某校进行了“防溺水”安全知识的测试.从七年级随机抽取了50名学生的测试成绩(百分制),整理样本数据,得到下表:
成绩 90≤x≤100 80≤x<90 70≤x<80 60≤x<70 x<60
人数 25 15 5 4 1
根据抽样调查结果,估计该校七年级600名学生中,80分(含80分)以上的学生有________人.
三、解答题
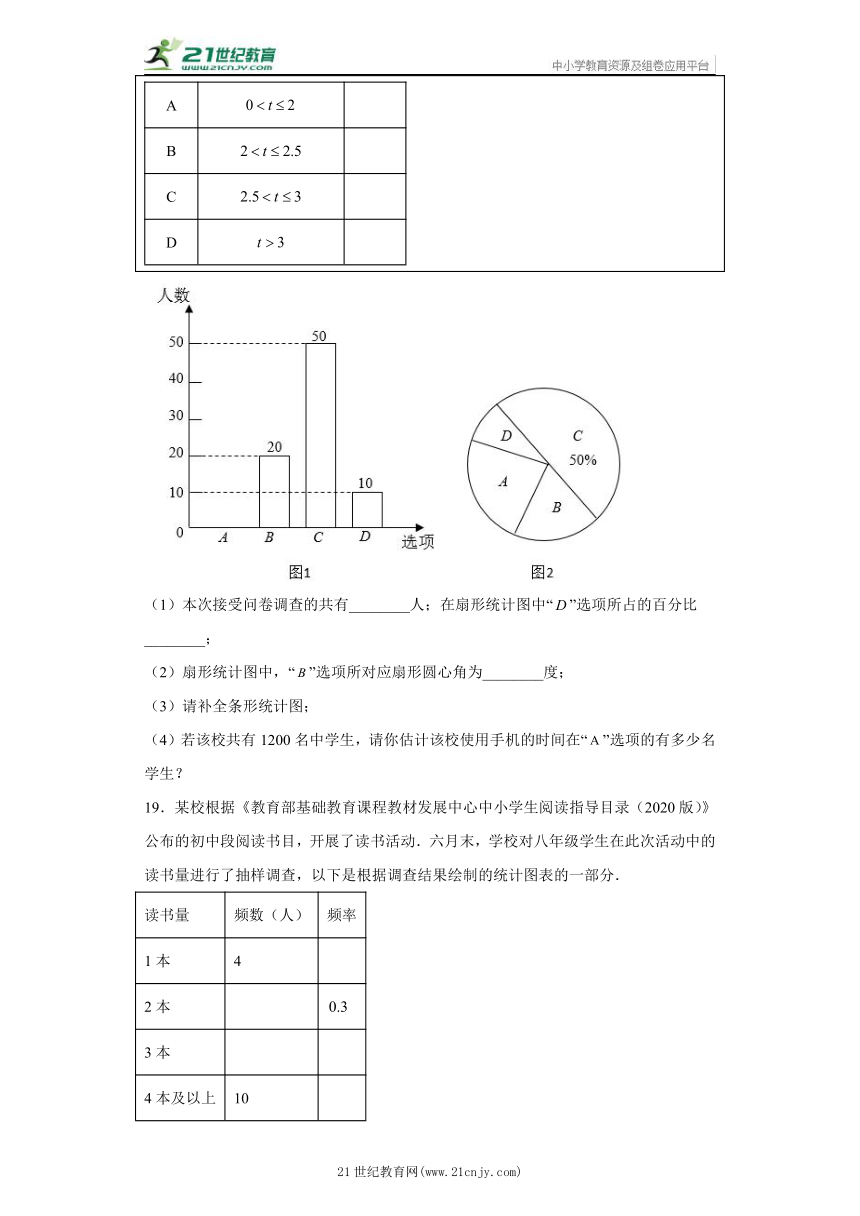
18.随着科技的不断发展,越来越多的中学生拥有了自己的手机,某中学课外兴趣小组对使用手机的时间做了调查:随机抽取了该校部分使用手机的中学生进行调查(问卷调查表如图所示),并用调查结果绘制了图1、图2两种“周使用手机的时间统计图”(均不完整),请根据统计图表解答以下问题:
中学生每周使用手机的时间问卷调查表
您好!这是一份关于您平均每周使用手机人数时间的问调查表,请在表格中选择一项符合您使用时间的选项,在其后空格内打“√”,非常感谢您的合作.选项使用时间(小时)ABCD
(1)本次接受问卷调查的共有________人;在扇形统计图中“”选项所占的百分比________;
(2)扇形统计图中,“”选项所对应扇形圆心角为________度;
(3)请补全条形统计图;
(4)若该校共有1200名中学生,请你估计该校使用手机的时间在“”选项的有多少名学生?
19.某校根据《教育部基础教育课程教材发展中心中小学生阅读指导目录(2020版)》公布的初中段阅读书目,开展了读书活动.六月末,学校对八年级学生在此次活动中的读书量进行了抽样调查,以下是根据调查结果绘制的统计图表的一部分.
读书量 频数(人) 频率
1本 4
2本
3本
4本及以上 10
根据以上信息,解答下列问题:
(1)被调查学生中,读书量为1本的学生数为______人,读书量达到4本及以上的学生数占被调查学生总人数的百分比为______%;
(2)被调查学生的总人数为______人,其中读书量为2本的学生数为______人;
(3)若该校八年级共有550名学生,根据调查结果,估计该校八年级学生读书量为3本的学生人数.
20.新冠疫情防控期间,全国中小学开展“停课不停学”活动.某市为了解初中生每日线上学习时长(单位:小时)的情况,在全市范围内随机抽取了名初中生进行调查,并将所收集的数据分组整理,绘制了如图所示的不完整的频数分布直方图和扇形统计图.
根据图中信息,解答下列问题:
(1)在这次调查活动中,采取的调查方式是_ (填写“全面调查”或“抽样调查”),_ .
(2)从该样本中随机抽取一名初中生每日线上学习时长,其恰好在“”范围的概率是 ;
(3)若该市有名初中生,请你估计该市每日线上学习时长在“”范围的初中生有_ 名.
21.某校为了了解初三年级名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:)分成五组;;;;,并依据统计数据绘制了如下两幅尚不完整的统计图.
解答下列问题:
这次抽样调查的样本容量是________,并补全频数分布直方图;
组学生的频率为________,在扇形统计图中组的圆心角是________度;
请你估计该校初三年级体重超过的学生大约有多少名?
参考答案:
1.B
【解析】
【分析】
根据频数分布直方图得出各分数段内的人数,再据此对各选项逐一判断即可.
【详解】
A.得分在70~80分之间的人数最多,有14人,故此选项正确,不符合题意,
B.及格(不低于60分)的人数为12+14+8+2=36(人),故此选项错误,符合题意,
C.∵总人数为4+12+14+8+2=40(人),得分在90~100分之间的人数为2人,
∴得分在90~100分之间的人数占总人数的百分比为×100%=5%,故此选项正确,不符合题意;
D.该班的总人数为40,故此选项正确,不符合题意,
故选:B.
【点睛】
本题考查条形统计图,正确提取图中信息是解题关键.
2.C
【解析】
【分析】
总体是指考查的对象的全体;个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.
【详解】
解:A、总体是七年级15000名学生的体重情况,这500名学生的体重是样本,故A错误;
B、个体是七年级每一名学生的体重,故B错误;
C、这500名学生的体重是总体的一个样本,故C正确;
D、样本容量是500,故D错误;
故选:C.
【点睛】
解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.
3.B
【解析】
【分析】
根据频数与频率的关系,审清题意频数之和等于所有数据的个数,频率之和等于1,即可得解.
【详解】
A. 频数分布表中,所有频率之和是1,故选项A不正确 ;
B. 频数之和等于所有数据的个数,故选项B正确;
C. 在频数分布表中,所有频数之和与所有数据的个数有关 ,故选项C不正确;
D. 在频数分布表中,所有频数之和等于所有数据的个数,故选项D不正确.
故选择B.
【点睛】
本题考查频数分布表中的频数与频率问题,频数之和等于总数,频率之和等于1,注意区分是解题关键.
4.D
【解析】
【分析】
结合条形图和扇形图,求出样本人数,进而进行解答.
【详解】
解:A、本次抽样调查的样本容量是=5000,正确;
B、扇形图中的m为10%,正确;
C、样本中选择公共交通出行的有5000×50%=2500人,正确;
D、若“五一”期间到荆州观光的游客有50万人,则选择自驾方式出行的有50×40%=20万人,错误,
故选D.
【点睛】
本题考查了条形统计图、扇形统计图,熟悉样本、用样本估计总体等知识是解题的关键,另外注意学会分析图表.
5.C
【解析】
【详解】
【分析】观察直方图,根据直方图中提供的数据逐项进行分析即可得.
【详解】观察直方图,由图可知:
A. 最喜欢足球的人数最多,故A选项错误;
B. 最喜欢羽毛球的人数是最喜欢田径人数的两倍,故B选项错误;
C. 全班共有12+20+8+4+6=50名学生,故C选项正确;
D. 最喜欢田径的人数占总人数的=8 %,故D选项错误,
故选C.
【点睛】本题考查了频数分布直方图,从直方图中得到必要的信息进行解题是关键.
6.D
【解析】
【分析】
由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.由此,对各选项进行辨析即可.
【详解】
A、对我市中学生每周课外阅读时间情况的调查,人数众多,意义不大,应采用抽样调查,故此选项不符合题意;
B、对我市市民知晓“礼让行人”交通新规情况的调查,人数众多,意义不大,应采用抽样调查,故此选项不符合题意;
C、对我市中学生观看电影《厉害了,我的国》情况的调查,人数众多,意义不大,应采用抽样调查,故此选项不符合题意;
D、对我国首艘国产航母002型各零部件质量情况的调查,意义重大,应采用普查,故此选项符合题意;
故选D.
【点睛】
本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
7.A
【解析】
【详解】
试题解析:长方形高的比等于10:15:25:35:10=2:3:5:7:2.
故选A.
8.D
【解析】
【分析】
利用频数分布直方图中的信息一一判断即可.
【详解】
解:A、小文一共抽样调查了(人,故选项错误,
B、样本中当月使用“共享单车”次的人数最多,有20人,故选项错误,
C、样本中当月使用“共享单车”不足30次的人数有26人,故选项错误,
D、样本中当月使用“共享单车”次的人数为12人,当月使用“共享单车”不足30次的人数有26人,所以样本中当月使用次数不足30次的人数多于次的人数,故选项正确,
故选:D.
【点睛】
本题考查频数分布直方图,解题关键是读懂图像信息,灵活应用所学知识解决问题.
9.D
【解析】
【分析】
首先知共有20个数据,根据公式:频数=频率×总数,知要使其频率为0.2,其频数应为4,然后观察选项中哪组数据包含样本中的数据有4个即可求解.
【详解】
解:这组数据共20个,要使其频率为0.2,则频数为:20×0.2=4个,
选项A中包含的数据有:6和7,其频数为2;
选项B中包含的数据有:8,8,8,9,9,9,其频数为6;
选项C中包含的数据有:10,10,10,10,10,11,11,11,其频数为8;
选项D中包含的数据有:12,12,12,13,其频数为4,
故选:D.
【点睛】
本题考查了频数与频率的概率,掌握公式“频数=频率×总数”是解决本题的关键.
10.C
【解析】
【分析】
根据样本、总体、个体、抽样调查和全面调查的性质,对各个选项逐个分析,即可得到答案.
【详解】
4300名学生的体重情况是总体,故选项A错误;
每名学生的体重情况是总体的一个个体,故选项B错误;
500名学生的体重情况是总体的一个样本,故选项C正确;
以上调查是抽样调查,故选项D错误;
故选:C.
【点睛】
本题考查了调查统计的知识;解题的关键是熟练掌握样本、总体、个体、抽样调查和全面调查的性质,从而完成求解.
11.0.575
【解析】
【分析】
由表格中的数据可知,4年增长了8.9-6.6=2.3万亿元,所以平均每年比上一年增长的GDP可由式子2.3÷4求出.
【详解】
解:∵2000年的国内生产总值为8.9万亿元,1996年国内生产总值为6.6万亿元,
∴平均每年比上一年增长的GDP为:(8.9-6.6)÷4=0.575(万亿元).
故答案为0.575.
12.8
【解析】
【分析】
求出最大值和最小值的差,然后除以组距,用进一法取整数值就是组数.
【详解】
解:123-50=73,
73÷10=7.3,
所以应该分成8组,
故答案为:8.
【点睛】
本题考查频率分布表中组数的确定,关键是求出最大值和最小值的差,然后除以组距,用进一法取整数值就是组数.
13.86.4°
【解析】
【分析】
用360°乘以最喜爱乒乓球的人数的比例即可.
【详解】
解:由题意得
.
故答案为:86.4°.
【点睛】
本题考查扇形统计图及相关计算,在扇形统计图中,每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°的比.
14.①
【解析】
【分析】
根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似解答.
【详解】
解:①了解全班同学每周体育锻炼的时间,适宜采用全面调查的方式;
②调查某批次汽车的抗撞击能力,适宜用抽样调查方式;
③调查新闻联播的收视率,适宜用抽样调查方式;
故答案为:①.
【点睛】
本题考查的是抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
15.②④③①
【解析】
【分析】
根据题意和频数分布表、扇形统计图制作的步骤,可以解答本题.
【详解】
解:正确统计步骤的顺序是:
②去图书馆收集学生借阅图书的记录;
④整理借阅图书记录并绘制频数分布表;
③绘制扇形图来表示各个种类所占的百分比;
①从扇形图中分析出最受学生欢迎的种类;
故答案为:②④③①.
【点睛】
本题考查扇形统计图、频数分布表,解答本题的关键是明确制作频数分布表和扇形统计图的制作步骤.
16.48
【解析】
【详解】
从左至右各长方形的高的比为2:3:4:6:1,
即频率之比为2:3:4:6:1;第二组的频率为,第二组的频数为9,
故则全班上交的作品有9÷=48,
故答案为48.
17.480
【解析】
【分析】
用七年级的学生总数乘以样本中80分以上的比例即可得到答案.
【详解】
600×=480(人)
故答案为:480.
【点睛】
本题考查了频数分布图、用样本估计总体,解答本题的关键是明确题意,由样本数据可以估计总体;
18.(1)100,10% (2)72 (3)见解析 (4)240人
【解析】
【分析】
(1)由C选项人数及其所占百分比可得总人数,用D选项人数除以总人数可得D选项对应百分比;
(2)先求出B选项占总人数的百分比,然后用360°该百分比即可求解;
(3)用总人数减去B、C、D人数求出A的人数即可补全图形;
(4)利用样本估计总体思想求解可得.
【详解】
解:(1)本次接受问卷调查的共有50÷50%=100(人),
在扇形统计图中“D”选项所占的百分比为10÷100×100%=10%;
(2)“B”选项人数占总人数的百分比为:20÷100×100%=20%,
故扇形统计图中,“B”选项所对应扇形圆心角为:20%×360°=72°;
(3)“A”选项人数为100-20-50-10=20(人),
故补全条形统计图如下所示:
(4)“A”选项人数占总人数的百分比为:20÷100×100%=20%,
估计该校1200人中使用手机的时间在“A”选项的学生有:1200×20%=240(人) .
【点睛】
本题考查条形统计图、用样本估计总体、扇形统计图,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
19.(1);(2);(3)人.
【解析】
【分析】
(1)由频数分布表与扇形统计图中的信息可得答案;
(2)读书量达到4本及以上的学生数为人,占被调查学生总人数的百分比为,可得总人数,利用总人数与读书量为2本的学生数的频率为,可得读书量为2本的学生数.
(3)利用样本中的学生读书量为3本的频率估计全年级的读书量为3本的学生人数,从而可得答案.
【详解】
解:(1)由频数分布表中得:读书量为1本的学生数为人,由扇形统计图得:读书量达到4本及以上的学生数占被调查学生总人数的百分比为
故答案为:
(2)由频数分布表中得:读书量达到4本及以上的学生数为人,
被调查学生的总人数为:(人),
由读书量为2本的学生数的频率为,
所以读书量为2本的学生数为:(人).
故答案为:
(3)由被调查的人中,学生读书量为3本的学生人数有:
人,
所以550名学生中学生读书量为3本的学生人数有:
(人).
答:550名学生中学生读书量为3本的学生人数有人.
【点睛】
本题考查的是从频数分布表与扇形统计图中获取信息,利用信息作决策,同时考查用样本估计总体,掌握以上知识是解题的关键.
20.(1)抽样调查; (2) ;(3)1200
【解析】
【分析】
(1)先根据全面调查和抽样调查的定义进行判断,再根据1≤t<2时,在频数分布直方图和扇形统计图中的数据,计算即可求解.
(2)由(1)知总人数,根据频数分布直方图,求出时的人数,计算即可求解.
(3)由(1)知总人数,求出时的人数所占比例,计算即可求解.
【详解】
(1)根据"在全市范围内随机抽取了名初中生进行调查"可知,采取的调查方式是抽样调查.
由频数分布直方图可知:当1≤t<2,有100名;
由扇形统计图可知,当1≤t<2,人数占总人数的20%,
则总人数=名.
即n=500.
(2)由(1)可知,n=500
从频数分布直方图中,可得:
当时,人数=500-50-100-160-40=150名.
∴恰好在的范围的概率.
(3)由(1)可知,n=500.
从频数分布直方图中,可得:
当时,有40人,占总人数.
∴该市每日线上学习时长在“”范围的初中生有.
【点睛】
本题主要考查频数分布直方图和扇形统计图的应用,熟练掌握频数分布直方图和扇形统计图中数值的意义是解题的关键.
21.(1),图见解析;(2);;(3)名.
【解析】
【分析】
(1)利用 组学生的频数除以该组所占的百分比,可求出抽样调查的样本容量,再用抽样调查的样本容量减去其它组的频数,即可求出组学生的频数,然后补全频数分布直方图,即可求解;
(2)用组学生的频数除以抽样调查的样本容量,可得到组学生的频率,用组的频数除以抽样调查的样本容量,再乘以百分之百,即可求解;
(3)求出样本中体重超过的学生的频率,再乘以600,即可求解.
【详解】
解:(1)这次抽样调查的样本容量是,
组的频数,
补全频数分布直方图,如图:
由统计图可知,
组学生的频率是,
组的圆心角;
样本中体重超过的学生有(名),
该校初三年级体重超过的学生为:(名).
【点睛】
本题主要考查了频数直方分布图,扇形统计图,用样本估计总体,从频数直方分布图,扇形统计图准确获取信息是解题的关键.
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
一、单选题
1.某次考试中,某班级的数学成绩被绘制成了如图所示的频数分布直方图.下列说法错误的是( )
A.得分在70~80分之间的人数最多
B.及格(不低于60分)的人数为26
C.得分在90~100分之间的人数占总人数的5%
D.该班的总人数为40
2.为了解某市七年级15000名学生的体重情况,从中抽取了500名学生进行测量,这500名学生的体重是( )
A.总体 B.个体 C.总体的一个样本 D.样本容量
3.在频数分布表中,所有频数之和( )
A.是1 B.等于所有数据的个数
C.与所有数据的个数无关 D.小于所有数据的个数
4.荆州古城是闻名遐迩的历史文化名城,“五一”期间相关部门对到荆州观光游客的出行方式进行了随机抽样调查,整理后绘制了两幅统计图(尚不完整).根据图中信息,下列结论错误的是( )
A.本次抽样调查的样本容量是5000
B.扇形图中的m为10%
C.样本中选择公共交通出行的有2500人
D.若“五一”期间到荆州观光的游客有50万人,则选择自驾方式出行的有25万人
5.某班组织了针对全班同学关于“你最喜欢的一项体育活动”的问卷调查后,绘制出频数分布直方图,由图可知,下列结论正确的是( )
最喜欢篮球的人数最多
B.最喜欢羽毛球的人数是最喜欢乒乓球人数的两倍
C.全班共有50名学生
D.最喜欢田径的人数占总人数的10 %
6.下列调查中,最适合采用全面调查(普查)的是( )
A.对我市中学生每周课外阅读时间情况的调查
B.对我市市民知晓“礼让行人”交通新规情况的调查
C.对我市中学生观看电影《厉害了,我的国》情况的调查
D.对我国首艘国产航母002型各零部件质量情况的调查
7.某频数分布直方图中,共有A,B,C,D,E五个小组,频数分别为10,15,25,35,10,则直方图中,长方形高的比为( )
A.2∶3∶5∶7∶2 B.1∶3∶4∶5∶1 C.2∶3∶5∶6∶2 D.2∶4∶5∶4∶2
8.“共享单车”为人们提供了一种经济便捷、绿色低碳的共享服务,成为城市交通出行的新方式,小文对他所在小区居民当月使用“共享单车”的次数进行了抽样调查,并绘制成了如图所示的频数分布直方图(每一组含前一个边界值,不含后一个边界值),则下列说法正确的是( )
A.小文一共抽样调查了20人
B.样本中当月使用“共享单车”次的人数最多
C.样本中当月使用“共享单车”不足30次的人数有14人
D.样本中当月使用次数不足30次的人数多于次的人数
9.已知一组数据8,6,10,10,13,11,8,10,12,12,9,8,7,12,9,11,9,10,11,10.那么频率是0.2的一组数据的范围是( )
A. B. C. D.
10.为了解我县参加2021年中考的4300名学生的体重情况,随机抽查了其中500名学生的体重进行统计分析,下列叙述正确的是( )
A.4300名学生是总体 B.每名学生是总体的一个个体
C.500名学生的体重情况是总体的一个样本 D.以上调查是普查
二、填空题
11.下表是某报纸公布的我国“九五”期间国内生产总值(GDP)的统计表,那么这几年间我国国内生产总值平均每年比上一年增长___万亿元.
年份 1996 1997 1998 1999 2000
GDP/万亿元 6.6 7.3 7.9 8.2 8.9
12.一个容量为的样本最大值是,最小值是,用频数分布直方图描述这一组数据,取组距为,则可以分成________组.
13.“阳光体育”运动在我市轰轰烈烈开展,为了解同学们最爱好的阳光体育运动项目,小王对本班50名同学进行了跳绳、羽毛球、篮球、乒乓球、踢毽子等运动项目最喜爱人数的调查,并根据调查结果绘制了如图所示的条形统计图,若将其转化为扇形统计图,那么最喜爱乒乓球的人数所在扇形区域的圆心角的度数为________.
14.以下调查:①了解全班同学每周体育锻炼的时间;②调查某批次汽车的抗撞击能力;③调查新闻联播的收视率.其中,适合全面调查的是__(填序号即可).
15.某同学要统计本校图书馆最受学生欢迎的图书种类,以下是打乱顺序的统计步骤:
①从扇形图中分析出最受学生欢迎的种类;
②去图书馆收集学生借阅图书的记录;
③绘制扇形图来表示各个种类所占的百分比;
④整理借阅图书记录并绘制频数分布表,正确统计步骤的顺序是_____.
16.为迎接学校艺术节,七年级某班进行班级歌词征集活动,作品上交时间为星期一至星期五.班委会把同学们上交作品件数按每天一组分组统计,绘制了频数分布直方图如下.已知从左至右各长方形的高的比为2:3:4:6:1,第二组的频数为9,则全班上交的作品有____件.
17.永州市教育部门为了了解全市中小学安全教育情况,对某校进行了“防溺水”安全知识的测试.从七年级随机抽取了50名学生的测试成绩(百分制),整理样本数据,得到下表:
成绩 90≤x≤100 80≤x<90 70≤x<80 60≤x<70 x<60
人数 25 15 5 4 1
根据抽样调查结果,估计该校七年级600名学生中,80分(含80分)以上的学生有________人.
三、解答题
18.随着科技的不断发展,越来越多的中学生拥有了自己的手机,某中学课外兴趣小组对使用手机的时间做了调查:随机抽取了该校部分使用手机的中学生进行调查(问卷调查表如图所示),并用调查结果绘制了图1、图2两种“周使用手机的时间统计图”(均不完整),请根据统计图表解答以下问题:
中学生每周使用手机的时间问卷调查表
您好!这是一份关于您平均每周使用手机人数时间的问调查表,请在表格中选择一项符合您使用时间的选项,在其后空格内打“√”,非常感谢您的合作.选项使用时间(小时)ABCD
(1)本次接受问卷调查的共有________人;在扇形统计图中“”选项所占的百分比________;
(2)扇形统计图中,“”选项所对应扇形圆心角为________度;
(3)请补全条形统计图;
(4)若该校共有1200名中学生,请你估计该校使用手机的时间在“”选项的有多少名学生?
19.某校根据《教育部基础教育课程教材发展中心中小学生阅读指导目录(2020版)》公布的初中段阅读书目,开展了读书活动.六月末,学校对八年级学生在此次活动中的读书量进行了抽样调查,以下是根据调查结果绘制的统计图表的一部分.
读书量 频数(人) 频率
1本 4
2本
3本
4本及以上 10
根据以上信息,解答下列问题:
(1)被调查学生中,读书量为1本的学生数为______人,读书量达到4本及以上的学生数占被调查学生总人数的百分比为______%;
(2)被调查学生的总人数为______人,其中读书量为2本的学生数为______人;
(3)若该校八年级共有550名学生,根据调查结果,估计该校八年级学生读书量为3本的学生人数.
20.新冠疫情防控期间,全国中小学开展“停课不停学”活动.某市为了解初中生每日线上学习时长(单位:小时)的情况,在全市范围内随机抽取了名初中生进行调查,并将所收集的数据分组整理,绘制了如图所示的不完整的频数分布直方图和扇形统计图.
根据图中信息,解答下列问题:
(1)在这次调查活动中,采取的调查方式是_ (填写“全面调查”或“抽样调查”),_ .
(2)从该样本中随机抽取一名初中生每日线上学习时长,其恰好在“”范围的概率是 ;
(3)若该市有名初中生,请你估计该市每日线上学习时长在“”范围的初中生有_ 名.
21.某校为了了解初三年级名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:)分成五组;;;;,并依据统计数据绘制了如下两幅尚不完整的统计图.
解答下列问题:
这次抽样调查的样本容量是________,并补全频数分布直方图;
组学生的频率为________,在扇形统计图中组的圆心角是________度;
请你估计该校初三年级体重超过的学生大约有多少名?
参考答案:
1.B
【解析】
【分析】
根据频数分布直方图得出各分数段内的人数,再据此对各选项逐一判断即可.
【详解】
A.得分在70~80分之间的人数最多,有14人,故此选项正确,不符合题意,
B.及格(不低于60分)的人数为12+14+8+2=36(人),故此选项错误,符合题意,
C.∵总人数为4+12+14+8+2=40(人),得分在90~100分之间的人数为2人,
∴得分在90~100分之间的人数占总人数的百分比为×100%=5%,故此选项正确,不符合题意;
D.该班的总人数为40,故此选项正确,不符合题意,
故选:B.
【点睛】
本题考查条形统计图,正确提取图中信息是解题关键.
2.C
【解析】
【分析】
总体是指考查的对象的全体;个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.
【详解】
解:A、总体是七年级15000名学生的体重情况,这500名学生的体重是样本,故A错误;
B、个体是七年级每一名学生的体重,故B错误;
C、这500名学生的体重是总体的一个样本,故C正确;
D、样本容量是500,故D错误;
故选:C.
【点睛】
解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.
3.B
【解析】
【分析】
根据频数与频率的关系,审清题意频数之和等于所有数据的个数,频率之和等于1,即可得解.
【详解】
A. 频数分布表中,所有频率之和是1,故选项A不正确 ;
B. 频数之和等于所有数据的个数,故选项B正确;
C. 在频数分布表中,所有频数之和与所有数据的个数有关 ,故选项C不正确;
D. 在频数分布表中,所有频数之和等于所有数据的个数,故选项D不正确.
故选择B.
【点睛】
本题考查频数分布表中的频数与频率问题,频数之和等于总数,频率之和等于1,注意区分是解题关键.
4.D
【解析】
【分析】
结合条形图和扇形图,求出样本人数,进而进行解答.
【详解】
解:A、本次抽样调查的样本容量是=5000,正确;
B、扇形图中的m为10%,正确;
C、样本中选择公共交通出行的有5000×50%=2500人,正确;
D、若“五一”期间到荆州观光的游客有50万人,则选择自驾方式出行的有50×40%=20万人,错误,
故选D.
【点睛】
本题考查了条形统计图、扇形统计图,熟悉样本、用样本估计总体等知识是解题的关键,另外注意学会分析图表.
5.C
【解析】
【详解】
【分析】观察直方图,根据直方图中提供的数据逐项进行分析即可得.
【详解】观察直方图,由图可知:
A. 最喜欢足球的人数最多,故A选项错误;
B. 最喜欢羽毛球的人数是最喜欢田径人数的两倍,故B选项错误;
C. 全班共有12+20+8+4+6=50名学生,故C选项正确;
D. 最喜欢田径的人数占总人数的=8 %,故D选项错误,
故选C.
【点睛】本题考查了频数分布直方图,从直方图中得到必要的信息进行解题是关键.
6.D
【解析】
【分析】
由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.由此,对各选项进行辨析即可.
【详解】
A、对我市中学生每周课外阅读时间情况的调查,人数众多,意义不大,应采用抽样调查,故此选项不符合题意;
B、对我市市民知晓“礼让行人”交通新规情况的调查,人数众多,意义不大,应采用抽样调查,故此选项不符合题意;
C、对我市中学生观看电影《厉害了,我的国》情况的调查,人数众多,意义不大,应采用抽样调查,故此选项不符合题意;
D、对我国首艘国产航母002型各零部件质量情况的调查,意义重大,应采用普查,故此选项符合题意;
故选D.
【点睛】
本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
7.A
【解析】
【详解】
试题解析:长方形高的比等于10:15:25:35:10=2:3:5:7:2.
故选A.
8.D
【解析】
【分析】
利用频数分布直方图中的信息一一判断即可.
【详解】
解:A、小文一共抽样调查了(人,故选项错误,
B、样本中当月使用“共享单车”次的人数最多,有20人,故选项错误,
C、样本中当月使用“共享单车”不足30次的人数有26人,故选项错误,
D、样本中当月使用“共享单车”次的人数为12人,当月使用“共享单车”不足30次的人数有26人,所以样本中当月使用次数不足30次的人数多于次的人数,故选项正确,
故选:D.
【点睛】
本题考查频数分布直方图,解题关键是读懂图像信息,灵活应用所学知识解决问题.
9.D
【解析】
【分析】
首先知共有20个数据,根据公式:频数=频率×总数,知要使其频率为0.2,其频数应为4,然后观察选项中哪组数据包含样本中的数据有4个即可求解.
【详解】
解:这组数据共20个,要使其频率为0.2,则频数为:20×0.2=4个,
选项A中包含的数据有:6和7,其频数为2;
选项B中包含的数据有:8,8,8,9,9,9,其频数为6;
选项C中包含的数据有:10,10,10,10,10,11,11,11,其频数为8;
选项D中包含的数据有:12,12,12,13,其频数为4,
故选:D.
【点睛】
本题考查了频数与频率的概率,掌握公式“频数=频率×总数”是解决本题的关键.
10.C
【解析】
【分析】
根据样本、总体、个体、抽样调查和全面调查的性质,对各个选项逐个分析,即可得到答案.
【详解】
4300名学生的体重情况是总体,故选项A错误;
每名学生的体重情况是总体的一个个体,故选项B错误;
500名学生的体重情况是总体的一个样本,故选项C正确;
以上调查是抽样调查,故选项D错误;
故选:C.
【点睛】
本题考查了调查统计的知识;解题的关键是熟练掌握样本、总体、个体、抽样调查和全面调查的性质,从而完成求解.
11.0.575
【解析】
【分析】
由表格中的数据可知,4年增长了8.9-6.6=2.3万亿元,所以平均每年比上一年增长的GDP可由式子2.3÷4求出.
【详解】
解:∵2000年的国内生产总值为8.9万亿元,1996年国内生产总值为6.6万亿元,
∴平均每年比上一年增长的GDP为:(8.9-6.6)÷4=0.575(万亿元).
故答案为0.575.
12.8
【解析】
【分析】
求出最大值和最小值的差,然后除以组距,用进一法取整数值就是组数.
【详解】
解:123-50=73,
73÷10=7.3,
所以应该分成8组,
故答案为:8.
【点睛】
本题考查频率分布表中组数的确定,关键是求出最大值和最小值的差,然后除以组距,用进一法取整数值就是组数.
13.86.4°
【解析】
【分析】
用360°乘以最喜爱乒乓球的人数的比例即可.
【详解】
解:由题意得
.
故答案为:86.4°.
【点睛】
本题考查扇形统计图及相关计算,在扇形统计图中,每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°的比.
14.①
【解析】
【分析】
根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似解答.
【详解】
解:①了解全班同学每周体育锻炼的时间,适宜采用全面调查的方式;
②调查某批次汽车的抗撞击能力,适宜用抽样调查方式;
③调查新闻联播的收视率,适宜用抽样调查方式;
故答案为:①.
【点睛】
本题考查的是抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
15.②④③①
【解析】
【分析】
根据题意和频数分布表、扇形统计图制作的步骤,可以解答本题.
【详解】
解:正确统计步骤的顺序是:
②去图书馆收集学生借阅图书的记录;
④整理借阅图书记录并绘制频数分布表;
③绘制扇形图来表示各个种类所占的百分比;
①从扇形图中分析出最受学生欢迎的种类;
故答案为:②④③①.
【点睛】
本题考查扇形统计图、频数分布表,解答本题的关键是明确制作频数分布表和扇形统计图的制作步骤.
16.48
【解析】
【详解】
从左至右各长方形的高的比为2:3:4:6:1,
即频率之比为2:3:4:6:1;第二组的频率为,第二组的频数为9,
故则全班上交的作品有9÷=48,
故答案为48.
17.480
【解析】
【分析】
用七年级的学生总数乘以样本中80分以上的比例即可得到答案.
【详解】
600×=480(人)
故答案为:480.
【点睛】
本题考查了频数分布图、用样本估计总体,解答本题的关键是明确题意,由样本数据可以估计总体;
18.(1)100,10% (2)72 (3)见解析 (4)240人
【解析】
【分析】
(1)由C选项人数及其所占百分比可得总人数,用D选项人数除以总人数可得D选项对应百分比;
(2)先求出B选项占总人数的百分比,然后用360°该百分比即可求解;
(3)用总人数减去B、C、D人数求出A的人数即可补全图形;
(4)利用样本估计总体思想求解可得.
【详解】
解:(1)本次接受问卷调查的共有50÷50%=100(人),
在扇形统计图中“D”选项所占的百分比为10÷100×100%=10%;
(2)“B”选项人数占总人数的百分比为:20÷100×100%=20%,
故扇形统计图中,“B”选项所对应扇形圆心角为:20%×360°=72°;
(3)“A”选项人数为100-20-50-10=20(人),
故补全条形统计图如下所示:
(4)“A”选项人数占总人数的百分比为:20÷100×100%=20%,
估计该校1200人中使用手机的时间在“A”选项的学生有:1200×20%=240(人) .
【点睛】
本题考查条形统计图、用样本估计总体、扇形统计图,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
19.(1);(2);(3)人.
【解析】
【分析】
(1)由频数分布表与扇形统计图中的信息可得答案;
(2)读书量达到4本及以上的学生数为人,占被调查学生总人数的百分比为,可得总人数,利用总人数与读书量为2本的学生数的频率为,可得读书量为2本的学生数.
(3)利用样本中的学生读书量为3本的频率估计全年级的读书量为3本的学生人数,从而可得答案.
【详解】
解:(1)由频数分布表中得:读书量为1本的学生数为人,由扇形统计图得:读书量达到4本及以上的学生数占被调查学生总人数的百分比为
故答案为:
(2)由频数分布表中得:读书量达到4本及以上的学生数为人,
被调查学生的总人数为:(人),
由读书量为2本的学生数的频率为,
所以读书量为2本的学生数为:(人).
故答案为:
(3)由被调查的人中,学生读书量为3本的学生人数有:
人,
所以550名学生中学生读书量为3本的学生人数有:
(人).
答:550名学生中学生读书量为3本的学生人数有人.
【点睛】
本题考查的是从频数分布表与扇形统计图中获取信息,利用信息作决策,同时考查用样本估计总体,掌握以上知识是解题的关键.
20.(1)抽样调查; (2) ;(3)1200
【解析】
【分析】
(1)先根据全面调查和抽样调查的定义进行判断,再根据1≤t<2时,在频数分布直方图和扇形统计图中的数据,计算即可求解.
(2)由(1)知总人数,根据频数分布直方图,求出时的人数,计算即可求解.
(3)由(1)知总人数,求出时的人数所占比例,计算即可求解.
【详解】
(1)根据"在全市范围内随机抽取了名初中生进行调查"可知,采取的调查方式是抽样调查.
由频数分布直方图可知:当1≤t<2,有100名;
由扇形统计图可知,当1≤t<2,人数占总人数的20%,
则总人数=名.
即n=500.
(2)由(1)可知,n=500
从频数分布直方图中,可得:
当时,人数=500-50-100-160-40=150名.
∴恰好在的范围的概率.
(3)由(1)可知,n=500.
从频数分布直方图中,可得:
当时,有40人,占总人数.
∴该市每日线上学习时长在“”范围的初中生有.
【点睛】
本题主要考查频数分布直方图和扇形统计图的应用,熟练掌握频数分布直方图和扇形统计图中数值的意义是解题的关键.
21.(1),图见解析;(2);;(3)名.
【解析】
【分析】
(1)利用 组学生的频数除以该组所占的百分比,可求出抽样调查的样本容量,再用抽样调查的样本容量减去其它组的频数,即可求出组学生的频数,然后补全频数分布直方图,即可求解;
(2)用组学生的频数除以抽样调查的样本容量,可得到组学生的频率,用组的频数除以抽样调查的样本容量,再乘以百分之百,即可求解;
(3)求出样本中体重超过的学生的频率,再乘以600,即可求解.
【详解】
解:(1)这次抽样调查的样本容量是,
组的频数,
补全频数分布直方图,如图:
由统计图可知,
组学生的频率是,
组的圆心角;
样本中体重超过的学生有(名),
该校初三年级体重超过的学生为:(名).
【点睛】
本题主要考查了频数直方分布图,扇形统计图,用样本估计总体,从频数直方分布图,扇形统计图准确获取信息是解题的关键.
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
